螺纹插装式溢流阀阀套内锥面制造的误差控制

张 祝，肖名涛，沈陆明，童成前

1) 苏州萨伯工业设计有限公司，苏州 215131 2) 南京萨伯工业设计研究院有限公司，南京 211399 3) 湖南农业大学机电工程学院，长沙 410128 4) 湖南农业大学信息与智能科学技术学院，长沙 410128 5) 北京汽车集团越野车有限公司，北京 101399

螺纹插装式溢流阀阀套内锥面自身角度误差会影响其静、动态特性[1-4]，且采用碳氮共渗后磨削的精加工工艺，需要控制其轴向磨削量，因碳氮共渗层较浅，磨削量太大会造成硬度大幅度降低[5-6]，影响其使用寿命.当溢流阀处于非满流量分布溢流时，因复杂的流场变化而产生冲击振动[7]，同时伴随气蚀现象产生，阀套内锥面在振动和气蚀的共同作用下[8-9]，表面硬化层太薄会很容易脱离基体，造成永久性破坏[3].现行设计制造过程中，一般图纸上对内锥面磨削的技术要求标定见光即可，但内锥面的磨削无法直观可见，对于常规内圆磨进给量的控制和见光的程度存在较大的随机性，最终影响批量制造产品质量的稳定性.尤其对于不具备数控磨削的中小型企业，在制造过程中，磨削内锥面完全由操作人员凭自身感觉来判断进给量，没有进行准确的磨削量检测控制，实际制造过程中即便有三坐标测量仪，也不可能做到对每个零件都采用三坐标检测.

基于此，对阀套结构及制造工艺进行分析，建立内锥面误差模型，通过模型分析得到磨削量与偏差角之间的变化关系；对误差模型进行应用分析，得到最大、最小磨削量及磨削公差随上、下偏差角的变化特性，该变化特性可指导实际磨削时的偏差取向选择，并确定适宜的上下偏差角数值.根据阀套结构特点设计专用的检测装置，分析检测误差并进行控制，以减小测量系统误差对测量精度的影响；通过实验验证了内锥面误差模型的准确性，所设计的检测装置能够满足测量精度的要求；在实际制造过程中，可应用检测装置快速测量每一件阀套内锥面的相关尺寸，实现制造误差的全覆盖精准控制.

1 阀套介绍

如图1和2所示，阀芯设置于阀套内，阀芯的密封圆与其左端面形成密封线，密封线与内锥面接触形成接触密封圆，接触圆直径与密封圆直径一致，接触圆所在平面为密封接触截面，外锥面与阀块接触定位密封，内锥面的小圆直径为进油通径，锥面的大圆直径为内锥面与阀套内槽油腔端面形成的截圆直径，内锥角为内锥面的全角[2,4].阀套的补油弹簧力作用在定位基准面上，阀芯的复位弹簧力作用在阀芯内腔环形端面上，在F2的作用下密封线与内锥面接触密封，在F1和F2的共同作用下阀套与阀块接触密封，在高压油的作用下，阀芯的密封线与内锥面应力接触[10-12].

图 1 阀套阀芯装配图Fig.1 Assembly drawing of the valve sleeve and valve core

图 2 阀套结构图Fig.2 Structure of the valve sleeve

锥阀式高压溢流阀处于关闭状态时，阀套的内锥面承受阀芯的高压静态载荷，但在卸荷后关闭的瞬间会产生冲击，故对阀套的内锥面要求基体部分要具备一定的耐冲击韧性[2,12]，表层一定深度部分还要具备相应的硬度，同时满足耐磨、耐压和耐冲击的特性[5,12]，以达到预设计的使用寿命.针对该工况要求，阀套的材料工艺采用高强度调质料，在机加工时留有余量，而后进行碳氮共渗热处理，热处理后再对留有余量部分进行精加工.碳氮共渗层一般都比较浅，较为经济的层深要求为0.4～0.5 mm[13-14]，为了获得表面高硬度，如图3所示，内锥面渗层的最大法向磨削量必须控制在0.1 mm以内，即上偏差角、下偏差角达到极限位置时两端的最大磨削量均不得超出0.1 mm.

图 3 角度偏差分析原理图Fig.3 Schematic of angle deviation analysis

对于采用典型的金属应力接触锥面密封的溢流阀，大约90%的泄漏是由于液压油在微尺度上渗入内锥表面的凹凸不平所引起的[15]；在系统高压负荷时阀芯承载的静态载荷较高，接触密封圆处的内锥面承受较大的压应力，因阀套基体为调质料，内锥表面硬度太低或剩余渗层太浅，都会导致内锥面产生塑性或永久性变形，这不仅会造成泄漏，且在液压泵的脉动、管道弹性、液压油可压缩性及高急流、回流、漩涡等的共同作用下[3,16]，溢流阀会产生严重的颤振和气蚀，在损坏精密部件的同时，使系统压力失稳并伴随出现系统振动和较大幅度的压力漂移现象；虽然做了结构改进，在阀芯上设置了带有阻尼的滑阀芯[17]，但依然无法消除因上述原因带来的振动.基于对溢流阀的静、动态特性及使用寿命要求，在精加工阀套内锥面时必须严格控制其角度误差及剩余渗层深度.

热处理后的高硬度零件通常采用磨削或硬车削加工；虽然采用数控硬车能够较好的控制精度，但因阀套孔径较小、孔深较长，采用细长刀杆硬车内锥面会产生振动形成纹路；加之碳氮共渗仅表层高硬基体较软，残余应力的形成同时还受到切削用量的影响[18]，碳氮共渗件硬车削不但难以形成有效压应力还会造成相变并形成质变层，容易引起较早的剥落失效和疲劳裂纹[19]；且硬车崩碎屑形成的表面有利于点蚀[20]，将加速气蚀的永久性损坏，故不宜采用硬车削，适合采用磨削方式加工.常规磨削内锥面的制造误差控制主要依靠机床操作人员的自身技能来实现，进给时通过听声判别是否接触磨削，磨削量凭借经验进给，角度误差则结合进给量通过目测内锥面是否完全光亮确定，而磨削装夹时定位基准选择对制造误差控制的影响没有得到有效体现；如此的制造误差控制完全是随机的，尤其对于大批量生产无法做到产品质量的一致性，更无法精确控制各个阀套内锥面的剩余渗层深度.目前较为普遍采用人工方式修整砂轮，因角度修整误差较大，为了获得整个锥面的目测光亮，势必会造成潜在的磨削量人为增大，从而减小了渗层深度.影响制造误差的因素不仅是该道磨削工艺自身的操作控制方法，还包括影响磨削工艺的前道机加工误差、定位误差及热处理变形带来的磨削量随机误差，要准确的控制内锥面制造误差，不仅要全面分析影响因素，还应结合目前普遍的常规制造能力和检测手段，细化研究内锥面误差控制理论，并辅以便捷、精准的检测方法，实现批量制造的过程精准控制.

2 内锥角误差分析

2.1 误差模型建立

如图3所示，获得制造误差上下偏差的直接方式是在内锥面法向0.1 mm厚度所形成的梯形内拉对角线，两条对角线分别与理想内锥面形成的小夹角即为上下偏差的理论最大值，但按此获得的偏差值所依赖的梯形四个顶点并非该内锥面的设计基础参数项.内锥面的设计基础参数项为两端的大圆、小圆和锥角，大圆直径即为Di，小圆直径即为进油通径，锥角即为内锥角α.以内锥面的理论设计母线为中心建立误差模型，偏差角边界线以母线的中点做旋转，且偏差角边界线的延长线与内锥面大圆所在平面的交点不得超出最大法向磨削量限定的范围、偏差角边界线的延长线与进油通径所在圆柱面的交点亦不得超出最大法向磨削量所限定的范围.

鉴于内锥角并非90°，且基于梯形特性，延长线两端交点只有一端先达到极限位置，且当该端达到极限位置时，偏差角边界线与母线在同一平面内形成的小夹角即为偏差值.实际内锥角小于90°，故上偏差角边界线的上端先达到极限位置、下偏差角边界线的下端先达到极限位置；据此，上偏差角根据上极限端点和中心点求取，下偏差角根据下极限端点和中心点求取.采用该方式所求取的上下偏差角数值略小于通过拉对角线方式所得到的上下偏差值，故该值是对理论最大偏差值的进一步收缩.经运算后可得两者的计算方程式.

上偏差角β的计算方程式：

下偏差角θ的计算方程式：

式（1）、（2）中：ΔA为Di-Dp，mm.

2.2 误差模型应用分析

由式（1）和（2）可知，决定上偏差角和下偏差角的因素包括：大圆直径、进油通径、最大法向磨削量以及内锥角.以某型先导式溢流阀的设计为例，相关参数如表1所示.将既定的设计基础参数值分别代入式（1）和（2），换算出上偏差角为1.368°、下偏差角为1.339°；而基于表1中参数采用拉对角的方式获得的上偏差角为1.405°、下偏差角为1.374°，该应用所得值可进一步反应偏差模型是对上下偏差理论最大值的进一步约束.

表 1 溢流阀计算参数Table 1 Overflow valve calculation parameters

根据换算的上下偏差要求分析，密封圆轴向磨削量随着上下偏差角的变化而改变，经运算得内锥角处于上偏差状态时的最大磨削量计算方程式：

经运算得内锥角处于下偏差状态时的最大磨削量计算方程式：

当内锥角为理想值时，密封圆轴向磨削量可向零趋近，但实际内锥角存在偏差，而阀套内锥面几何形状的完整性直接影响到溢流阀的动态特性[21]和噪音生成[22]，为了保证整个内锥面的磨削完整性，对应内锥角的实际偏差状态，须对应限定该偏差值的密封圆轴向磨削量最小值.经运算得内锥角处于上偏差状态时的最小磨削量计算方程式：

经运算得内锥角处于下偏差状态时的最小磨削量计算方程式：

根据式（3）和（5）运算得上偏差时磨削公差计算方程式：

根据式（4）和（6）运算得下偏差时磨削公差计算方程式：

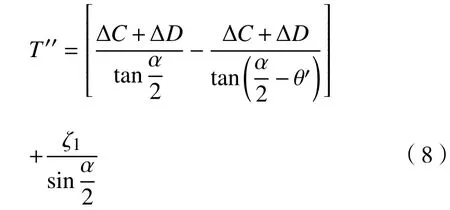
由式（3）和（4）可得，当内锥角为理想状态值时，密封圆法向磨削量与最大法向磨削量一致，密封圆轴向磨削量与最大法向磨削量对应轴向尺寸也一致，此时亦是密封圆轴向磨削量的最大值.由式（3）可得，随着上偏差角实际值的增大，上偏差时的密封圆轴向最大磨削量逐渐减小；由式（4）可得，随着下偏差角实际值的增大，下偏差时的密封圆轴向最大磨削量亦呈逐渐减小趋势；而上偏差磨削量变化率小于下偏差磨削量的变化率，两者的变化趋势特性如图4所示.

图 4 实际最大磨削量变化趋势Fig.4 Change trend of the actual maximum grinding amount

由式（5）和（6）可得，随着上偏差角实际值的增大，上偏差时的密封圆轴向最小磨削量逐渐增大；随着下偏差角实际值的增大，下偏差时的密封圆轴向最小磨削量亦呈逐渐增大趋势；上偏差磨削量变化率大于下偏差磨削量的变化率，两者的变化趋势特性如图5所示.

图 5 实际最小磨削量变化趋势Fig.5 Change trend of the actual minimum grinding amount

由式（7）和（8）可得，理论最大磨削公差值为0.186 mm，磨削公差变化特性曲线如图6所示；忽略微小趋势变化，磨削公差变化曲线关于上下偏差近似对称，即相同的上下偏差角度对应的磨削公差值近似相等，上下偏差的磨削公差变化率近似一致.

图 6 实际磨削公差变化趋势Fig.6 Variation trend of the actual grinding tolerance

因数值差的变化较小，图4～6中各曲线整体如粗实线所示呈近似线性变化，实际变化趋势如各图中虚线所示.

通过模型应用分析，相同的上下偏差角对应的最小磨削量和最大磨削量有明显差异，处于上偏差时的最小磨削量较处于下偏差时的最小磨削量大，处于上偏差时的最大磨削量较处于下偏差时的最大磨削量亦偏大.故在实际制造过程中，在获得相同的实际密封圆轴向磨削量公差值时，如为了提高生产效率，减少砂轮的磨损，调整砂轮修整角度时，在靠近理想设计值的同时，取内锥角处于下偏差状态较为有利；但若因热处理或其他因素带来内锥面变形，需要较大的轴向磨削量来拟补变形缺陷时，在靠近理想设计值的同时，取内锥角α处于上偏差状态较为有利.

当上偏差角实际值达到1°时，密封圆轴向磨削量公差值为0.0523 mm，而当上偏差角实际值达到1.3°时，密封圆轴向磨削量公差值只有0.0135 mm；当下偏差角实际值达到1°时，密封圆轴向磨削量公差值为0.0521 mm，而当下偏差角实际值达到1.3°时，密封圆轴向磨削量公差值只有0.0104 mm.由此可见，结合后续的实际制造工艺，通过式（1）和（2）获得的上下偏差角并不适合直接作为制造误差的极限值，结合内圆磨加工能力及其他因素对内锥角α的要求，可对制造误差初步约束为±1°.

3 内锥面制造误差控制

3.1 误差检测装置

在阀套的实际生产过程中，不可能做到用三坐标测量仪对每个零件都进行内锥角及密封圆轴向磨削量的全检，故需要设计专用的快速量具，以适用于实际制造的误差检测控制[23-24].

角度检测装置如图7所示，主要结构包括由一组同轴的几何要素组成：①与配合内孔间隙配合的检具外圆；②用于浮动支撑的环形槽；③用于对内锥面测量的大小检测外圆；④检测外圆和端面形成的接触锐角.检测大小圆分别位于检具主体两端，且在主体两端沿回转中心设置有工艺孔.检具主体机加工完成后进行高硬度处理，热处理后对工艺孔先行研磨，研磨后精磨检具外圆、环形槽支撑圆、检测大圆、检测小圆以及两端端面，保证精加工外圆的同轴度及两端端面相对于检测大小圆的垂直度，精加工后保持接触锐角的成型锐边，可采用手工软抛方式去除飞边毛刺.

图 7 角度检测装置结构图Fig.7 Structure of the angle detection device

磨削量检测装置基本结构和技术要求与角度检测装置相同，如图8所示，仅检测圆直径不同，且磨削量检测装置可设置为单头或双头，图示为单头，设置双头时，两端的检测密封圆直径一致，检测密封圆直径与密封外圆直径、接触密封圆直径一致.

图 8 磨削量检测装置结构图Fig.8 Structure of the grinding quantity detection device

鉴于阀套的配合内孔与检具外圆之间存在间隙，为了消除间隙影响以提高检测精度，采用软过盈的浮动支撑方式.如图9所示，用于浮动支撑的橡胶圈张紧套装于支撑圆上，橡胶圈设置数量≥2，套装后的橡胶圈与阀套的配合内孔处于过盈状态，浮动支撑过盈量为0.1～0.2 mm；挡圈为开口式，套装后挡圈外围距检具外圆保持径向间隙，挡圈间隙量为0.2～0.3 mm.

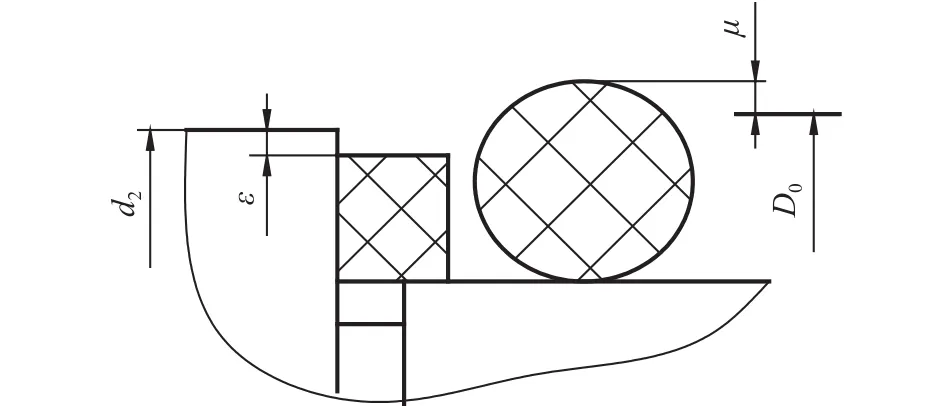
图 9 浮动支撑结构图Fig.9 Floating support structure drawing

检具外圆直径小于配合内孔直径的下偏差值，以该下偏差值为基础尺寸，公差为0～-0.01 mm.环形槽支撑圆直径根据选型的浮动支撑组件选定具体尺寸及公差，浮动支撑槽的槽宽及轴向位置，根据阀套的配合内孔相对内锥面的轴向位置确定，让整个槽处于配合内孔的轴向位置内，且位于槽两侧的检具外圆保持一段轴向量与配合内孔相对应配合.

根据下述的理论误差分析，检测小圆直径逼近进油通径，检测大圆直径逼近锥面大圆直径，保持直径差0.3～0.4 mm，以降低检测误差；检测大小圆端、密封圆端置入阀套内接触内锥面时，需限定检具长度，使其非检测端超出阀套端面3～5 mm.

3.2 误差检测原理

将内锥面母线作为斜边置于直角三角形中，在获知对应的两个直角边后即可换算出实际内锥角的半角.如图10所示，半角对边长度为检测大圆直径和检测小圆直径差值的一半，半角邻边长度为大圆检测轴向长度和小圆检测轴向长度的差值，其中L4和L5的长度检测是将检具两头分别置入阀套内，在大圆端与内锥面接触时测得的检具小圆端面与转移基准面的长度为L4，在小圆端与内锥面接触时测得的检具大圆端面与转移基准面的长度为L5.

图 10 角度检测原理图Fig.10 Schematic of angle detection

实际加工内锥角α′的计算方程式：

式中：α′为实际加工内锥角，(°).

实际加工内锥角为通过测量值间接获取的，可将其表示为实测值的多元函数[25]，根据误差理论，实际加工内锥角测量误差的方程式：

其线性化的误差传递公式（去高阶项）：

式中：Δd3为d3的测量误差；Δd4为d4的测量误差；ΔL4为L4的测量误差；ΔL5为L5的测量误差.以上各项误差的传递系数为：

由以上各误差传递系数可得检测大圆直径和检测小圆直径的差值越大，内锥角测量误差就越小.半角的对边和邻边长度都是检测的差值，各项检测值不可避免会有检测误差，但基于相同的检测装置，求取的差值可有效降低检测装置自身的系统误差带来的影响.

3.3 误差检测与控制

如图11所示，将工件置于工作台上，千分表安装于高度尺上，根据L4、L5、La、Lb的初步测得值校对千分表.检测内锥角时，将检具小圆端置入阀套内，测得转移基准面与检具大圆端面之间的尺寸L5；调头后将检具大圆端置入阀套内，测得转移基准面与检具小圆端面之间的尺寸L4；将测得值代入式（9）可得实际内锥角α′.检测密封圆轴向磨削量时，将检具测头端置入阀套内，先测得磨削前的转移基准面与检具外端面之间的尺寸La，待内锥面磨削后，再检测出转移基准面e与检具外端面之间的尺寸Lb，La与Lb的差值即为实际密封圆轴向磨削量.

图 11 检测示意图Fig.11 Measurement diagram

阀套在前道机加工过程中，内锥角精度由机床自身保证，但内锥面上接触密封圆相对转移基准面的轴向尺寸属于间接获取，会受到诸多因素的影响，因此在阀套热处理后，首先通过检测接触圆初始轴向位置尺寸进行分挡，磨削加工时以转移基准面作为轴向定位基准，按挡分批次调整磨削，如此可避免因内锥面相对转移基准面的轴向尺寸差异较大，造成的因磨削量偏差大带来的砂轮撞击或内锥面磨削不完整，最终影响生产效率及加工质量.

阀套试磨后检测接触圆磨削后轴向位置尺寸并计算出轴向磨削量的实际值.另对该试磨件内锥角按上述方法进行相关参数检测，根据式（9）换算出加工的实际内锥角并确认该值处于初步约束的公差范围内，同时计算出对应的实际偏差角，根据实际内锥角是处于上偏差或下偏差，将实际偏差角对应代入式（3）或式（4）、式（5）或式（6），换算出密封圆处对应该实际偏差角的轴向磨削量最大值和最小值，上述检测计算出的轴向磨削量实际值需落在该最大值和最小值范围内，试磨件方为合格品；若该试磨件的轴向磨削量实际值没有落在范围内，而实际内锥角落在初步约束范围内并趋近理想值，此时只需要计算出差值重新调整进给量即可，无须再次修整砂轮角度；若实际内锥角趋近上下偏差值或超出偏差值范围，可再次调整砂轮修整角度，再次试磨后重复上述检测过程，直至所有尺寸合格.

后续加工过程中，在无需提高内锥面角度误差精度时，砂轮修整角度一经确定不再调整修改，只需适时检测实际密封圆轴向磨削量即可控制整个内锥面磨削加工过程的精度.为了进一步提高内锥角的检测精度，可将试磨件用三坐标测量仪进行检测，将三坐标测量仪的检测值与所述检测方法的测得值进行对比，标定检测方法的测量误差，也可以制作标准角度的内锥角样件，对检测方法进行校对.

基于表1的参数样件，采用所述检测方法的相关测得数据如表2所示，经计算得密封圆轴向磨削量的实际值为0.039 mm、实际加工内锥角为65.42°.根据误差模型得到的密封圆轴向磨削量为0.041 mm，与测得值的差值仅为0.002 mm，相对于对应该角度的最大轴向磨削量，该测量误差可忽略.实际加工的内锥角处于上偏差，将上偏差角实际值 0.42°分别代入式（3）和（5）计算得最大磨削量为0.1698 mm，最小磨削量为0.0408 mm，实际加工内锥角度落在了初步约束的±1°公差范围内，但对应该内锥角的密封圆轴向磨削量未能达到最小磨削量的要求，需根据计算差值重新调整进给量.对样件内锥角采用三坐标测量得内锥角度为65.36°，将三坐标测得值偏差角实际值0.36°再次分别代入式（3）和（5）计算得最大磨削量为 0.1721 mm，最小磨削量为0.0350 mm.实验结果显示，所述检测方法的测量误差为0.06°，且由检测方法所得磨削量范围落在三坐标校对范围内，两者的最大磨削量差值为0.0023 mm、最小磨削量差值为0.0058 mm.

表 2 检测数据Table 2 Test data

通过上述实验验证了误差模型的准确性，但所述检测方法存在检测误差，如图12所示，经分析得影响检测误差的主要因素包括：因接触锐角圆度误差造成与锥面虚接触而产生的轴向尺寸测量误差、检具轴线与阀套轴线因间隙配合产生倾斜偏移造成的轴向尺寸测量误差、两端接触锐角圆所在平面的平行度误差造成的轴向尺寸测量误差.通过误差影响因素分析可得，降低误差方式主要体现在两个方面，一是提高检具自身的制造精度，包括接触锐角线的自身圆度、两端面之间的平行度、两端面与轴线的垂直度以及支撑圆与外圆之间的同轴度，二是尽可能降低检具与阀套之间配合间隙的影响，即上述采用软过盈配合方式所达到的效果.

图 12 测量误差因素.（a）两轴倾斜偏移；（b）两端面不平行Fig.12 Factors of measurement error: (a) two-axis tilt offset; (b) two ends are not parallel

综合考虑检测误差、制造精度及误差控制要求，在实际制造过程中内锥角的最终误差应控制在±0.8°以内，在此范围内，因内锥角检测误差造成的最大、最小磨削量范围偏差可得到补偿，对应该角度偏差的上偏差状态时密封圆轴向最小磨削公差为0.078 mm、下偏差状态时密封圆轴向最小磨削公差为0.08 mm.为了保障内锥面的磨削完整性，需对最小磨削量进行修正，需在对应实际加工内锥角计算值的基础上增加5 μm，实际磨削量向增加后的数值逼近，修正后的上偏差状态最小磨削公差为0.073 mm、下偏差状态最小磨削公差为0.075 mm，两者可统一为0.075 mm.

4 结论

通过实验验证，内锥角误差模型准确可靠，检测方法所获得精度满足误差控制要求，在实际工程应用中能够全面、精准、高效的控制内锥面的制造误差.

（1）基于制造工艺要求建立了对应的内锥角偏差模型，并由此获得内锥角制造误差的理论极限值为-1.339°～+1.368°；通过偏差模型应用分析，将内锥角误差极限值收缩为±1°，对应该内锥角初步约束值的密封圆轴向磨削量最小公差值为0.052 mm；对各变化趋势图中曲线分析，得知上下偏差状态直接影响最大、最小轴向磨削量，可根据实际磨削量的需要调整制造偏差状态，这对制造过程控制具有显著的指导意义.

（2）结合制造工艺设计的检测装置，能够快速、精准的检测实际制造的内锥角度及密封圆轴向磨削量，并有效的控制该角度偏差和对应的轴向磨削量超差；软过盈的浮动支撑方案提高了检测精度，通过标准件或三坐标测量仪校对，可进一步降低测量误差；通过误差检测原理分析，增大检测大、小圆直径可有效降低测量误差，且内锥角度计算采用测量后的差值，对相同的测量系统，采用差值可进一步降低系统自身误差对最终结果的影响；通过实验，内锥角测量误差为0.06°，密封圆轴向磨削量的测量误差为2 μm.

（3）热处理后对内锥面轴向尺寸进行分组，分组尺寸测量基准、磨削加工定位基准、轴向磨削量检测基准三者的基准统一，从而保证了内锥面批量制造精度的一致性；根据试磨件检测结果修正磨削参数，进一步降低制造误差，确定内锥角自身误差合格后，通过误差模型计算出对应的密封圆轴向磨削量的范围，后续加工只需检测该轴向磨削量是否落在计算所得值范围内，即可控制内锥面轴向位置的制造误差.

（4）根据实验结果调整内锥角的最终实际制造误差控制范围为±0.8°，密封圆轴向最小磨削公差在该内锥角范围对应的数值基础上做进一步修正，修正后的最小磨削公差为0.075 mm，调整修正后的偏差范围可补偿检测误差带来的潜在超差，使实际误差落在控制范围内.

（5）根据上述得到的内锥角偏差及轴向磨削量公差精度要求，中小型企业的常规设备制造能力及检测装置能够满足其要求，无需更换数控磨床及三坐标等高精加工和检测设备.