基于快速SR-UKF的锂离子动力电池SOC联合估计
2021-06-28章军辉陈大鹏
章军辉,李 庆,陈大鹏,赵 野
1) 中国科学院微电子研究所,北京 100029 2) 江苏物联网研究发展中心,无锡 214135 3) 无锡物联网创新中心有限公司,无锡 214135 4) 昆山微电子技术研究院,昆山 215347
锂离子动力电池是新能源电动汽车的重要供能来源,而电池生产工艺上的波动、材质本身的不均匀性,使得单体电池的容量、内阻、自放电特性等皆有一定的差异,并且随着充放电循环次数的增加以及车内特殊工作环境的影响,电池容量也会出现不同程度的衰减,进一步加剧了单体之间的差异性.准确的电池状态估计为电池成组、电池管理系统(Battery management system, BMS)均衡等用途提供可靠参考依据,从而对单体电池的充分合理利用、电池组使用寿命的延长以及整车运行效率的改善具有重要实际意义[1-2].
电池状态估计本身属于非线性估计问题,而针对非线性问题求解,常用手段包括非线性函数局部线性化[3-4]、概率密度分布逼近法[5-6]、神经网络法[7-8]等.其中,非线性函数局部线性化的主要方法有Taylor展开法[3]、插值多项式法[4];概率密度分布逼近的主要方法有确定性样本逼近法[5]、大量粒子逼近法[6].
目前,电池荷电状态(State of charge,SOC)估计方法主要有:(1)安时积分计量(Ampere-hour counting, AH)法[9],应用较广,不过算法本身缺少对内外在扰动因素进行补偿的措施,存在由SOC初值标定偏差而导致曲线始终不能收敛、计算累积误差等问题;(2)开路电压(Open circuit voltage, OCV)法[10-11],通过“浅放-静置”的方法拟合出OCV与SOC一一映射曲线,实现对SOC初值进行离线校正,其因需较长的静置时间而无法用于在线工况,一般是与其他方法结合使用;(3)扩展卡尔曼滤波(Extended Kalman filter, EKF) 法[12],仅利用Taylor展开式中的一阶偏导项对非线性函数进行线性化处理,再基于标准卡尔曼(Kalman filter, KF)框架完成状态估计,存在较低的截断精度、Jacobian矩阵计算繁杂、滤波性能不稳定等问题;(4)无迹卡尔曼滤波(Unscented Kalman filter,UKF)法[13],通过构造满足一定规则的确定性样本来逼近非线性系统的后验概率密度分布,相对EKF来说,其估计精度有明显改善,不过UKF无法保证滤波过程中状态误差协方差矩阵的非负定性,存在滤波发散的隐患,同时其估计精度也一定程度上受限于电池等效模型的准确性.(5)粒子滤波(Particle filter, PF)法[14],通过大量随机粒子来逼近非线性系统的后验概率密度分布,对于强非线性、非高斯系统具有潜在应用价值,不过PF存在粒子退化、重采样导致的样本贫化、计算负荷严重等问题.(6)神经网络法[8],通过神经网络学习的方法建立未知系统的非线性映射关系,无需准确的数学建模、非线性近似工作,可适用于各类电池的状态估计,不过其估计精度对数据集的依赖性较强.
目前,电池健康状态(State of health,SOH)估计方法主要概括为2大类:(1)基于特征的预测,通过建立容量、内阻等特征参数与电池寿命之间的对应关系,间接地对电池的老化程度进行预测.如内阻法[15],然而对于毫欧级的内阻来说,其量测难度较大;电化学阻抗谱(Electrochemical impedance spectroscopy, EIS)法[16],需专用仪器,常用于实验室分析.(2)基于数据驱动的预测,不需要对象系统的机理知识,利用测试数据挖掘出描述电池性能演变的潜在规律,进而对电池使用寿命进行预测.如支持向量机(Support vector machine, SVM)[17]、粒子滤波[14]、神经网络[8]等,该类方法通常由于实验数据的有限性、不确定性,而致使其在工程应用上存在着一定的局限性.
针对标准UKF算法本身存在着因状态误差协方差矩阵无法实现Cholesky分解而导致滤波发散的隐患,以及在电池状态估计过程中由离线标定的电池等效模型参数而造成的累积误差的问题,本文发展了一种基于快速SR-UKF的电池状态联合估计算法,首先构建二阶电池等效模型的状态空间方程,其次在循环迭代过程中对观测方程进行了准线性化处理,同时用状态误差协方差矩阵的平方根进行迭代运算,以防协方差矩阵负定而致滤波发散,接着设计了一种电池状态联合估计策略,对电池模型参数进行实时辨识,以确保电池等效模型的准确性与有效性,最后对本文设计的快速SR-UKF算法以及联合估计策略进行了验证与探讨.
1 数学建模
锂离子动力电池的二阶RC等效模型,能够较好地模拟电池的静动态特性,结构复杂度相对适中,便于电池特性分析,本文将采用二阶RC等效模型建立电池状态空间方程.
二阶RC等效电路如图1所示,其中,Et为电池的电动势,其测量方法可通过长时间静置使得电池内部处于平衡状态,此时量测出电池的端电压在数值上等于电池的平衡电动势,It为t时刻电池的放电电流,Re为电池的欧姆内阻,Rs、Rl为电池的极 化内阻,Cs、Cl为电池的极化电容,Ucs,t、Ucl,t为电池极化内阻上产生的压降,Uo,t为t时刻电池两端的观测电压.
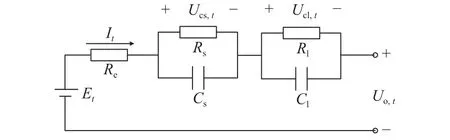
图 1 锂离子动力电池的二阶RC等效模型Fig.1 2nd-order RC model of Li-ion battery
1.1 电池SOC状态空间模型
根据图1所示的电池模型,作如下定义

式中,τs、τl为时间常数,表示U的微分.
电池荷电状态的安时积分计量法[6]定义为

式中,St0为电池t0时刻的荷电状态,即SOC初始值,Q0为电池的额定容量,η为充放电效率.
以x1(k)=[S(k),Ucs(k),Ucl(k)]T作为状态向量,y1(k)=Uo(k)作为系统输出,u(k)作为控制输入,w(k)、v(k)作为系统扰动,根据式(1)~(4),建立以x1(k)为状态向量的一步预测的离散状态空间方程:

式中,w(k)=[w1(k),w2(k),w3(k)]T为过程噪声,v(k)为观测噪声,u(k)=I(k),各系数矩阵满足

其中,Ts为采样周期,Et=f{S(k)}表示电池的平衡电动势Et与电池SOC之间的函数关系,该映射关系与环境温度、锂电池老化程度等因素有关.在电池SOC状态空间模型中,欧姆内阻Re、极化内阻Rl与Rs是事先已辨识的模型参数.
1.2 电池SOH状态空间模型
锂电池的健康状态可通过电池的欧姆内阻Re来间接评估[18].根据图1所示的电池模型,把电池的荷电状态、极化电压当作已知值,作如下定义

式中,rt为过程噪声,qt为观测噪声.
令x2(k)=Re(k),建立以x2(k)为状态变量的一步预测的离散状态空间方程:

式中,各系数满足

2 参数辨识
本文实验对象是合肥国轩公司的一个电池组,内含12串单体,每个单体标称容量为30 A·h.在25 ℃环境温度下,对该电池包进行“浅放-静置”的恒流脉冲放电试验:放电倍率为0.6 C,放电电流恒为18 A,单次放电时长为1 min并静置30 min,重复该操作直至放完.一个脉冲放电周期内的单体端电压变化过程如图2所示,其中V1、V2、V3表示量测的端电压.

图 2 一个脉冲放电周期内单体端电压响应曲线Fig.2 Dynamic curve of Uo in a pulse-periodic discharge
利用RC网络能够较好地描述电池的放电过程中的动态特性:
(1)在放电开始时刻,由于欧姆内阻上产生的压降,导致端电压瞬间抖降,随后由于给等效电容进行充电,端电压呈准指数函数下降;
(2)在放电结束时刻,由于欧姆内阻上的压降消失,导致端电压瞬间抖升,随后由于等效电容放电使得端电压进一步缓慢上升,最终趋于稳定,其中,V2-V1表示端电压相对快速的变化过程,V3-V2表示端电压相对缓慢的变化过程.
2.1 模型参数
通过图2所示的“浅放-静置”的恒流脉冲放电试验,对二阶RC网络模型参数进行辨识,模型参数初值见表1.

表 1 基于二阶RC网络的模型参数Table 1 Parameters of 2nd-order RC model
2.2 OCV-SOC曲线
在上述实验条件下,采用开路电压法[10]拟合出静置稳定后的开路电压与电池SOC之间的映射关系曲线,如图3所示.
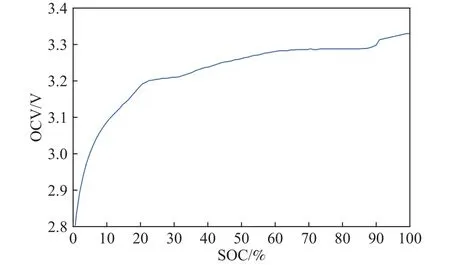
图 3 开路电压与SOC的关系曲线Fig.3 Relationship between open circuit voltage and SOC
通过图3映射关系可以为电池组提供一个相对准确的SOC初值,同时也可以对长时间静置后的电池进行SOC初值校正.标定完SOC初值后,再通过安时积分计量法[9]来在线估算电池SOC.而实际上由于安时积分计量法属于一种开环估计方法,当SOC初值标定不准的情况下,估计曲线始终是无法收敛于真实轨迹.
对于这一问题,接下来通过无迹卡尔曼滤波对安时积分计量法的估计值进行实时修正,以改善开环估算的效果.此外,考虑到电池老化、环境温度等扰动因素的影响,在工程实施时,宜拟合出多份OCV-SOC曲线.
3 电池状态估计
3.1 电池SOC估计算法
UKF滤波的核心是UT变换,即通过确定性采样构造Sigma点集来近似系统非线性函数的概率密度分布进而求解非线性滤波问题.不过,传统UKF算法在更新状态协方差时存在减法运算,不能保证协方差矩阵的非负定性,存在滤波发散的隐患.
为此,本文给出一种快速SR-UKF估计方法:在UKF滤波过程中,使用状态误差协方差矩阵的平方根进行迭代运算,以避免协方差矩阵负定而致滤波结果发散的缺陷[19-21];为了降低UKF的计算开销,在UT变换时对观测方程进行准线性化处理,建立开路电压与电池SOC的映射表,通过查表方法来减少对观测方程的数值计算.
3.1.1 定义
定义1.QR分解
若存在正定矩阵Qm×m与上三角矩阵Rm×n,使得Am×n=Qm×mRm×n,则称之为A的QR分解,且记R=qr{A}.
定义2.Cholesky因子
由定义1知,AT的QR分解,即,若矩阵P=AAT,有,则称为P的Cholesky因子,记为=chol{P}.
定义3.Cholesky因子的一阶更新
由定义2知,若已知P的Cholesky因子为,则称的Cholesky因子为的一阶更新,记为.
3.1.2 SR-UKF算法
算法设计如下:
(1)UT 变换.
a)构造2N+1维Sigma点集
利用随机向量的均值与协方差平方根来构造Sigma点集

为了能够更好地逼近系统状态的后验分布情况,对Sigma点集进行权值设计

式中,α是用来描述Sigma点集的偏离程度,取值范围为(10-4, 1);β是用来描述系统状态的分布情况,在高斯分布情况下取2;λ=α2(N+k)-N,影响逼近精度,其中,参数k通常取0.
b)对Sigma点集进行非线性变换
将a)中构造的Sigma点集,代入式(5)中得
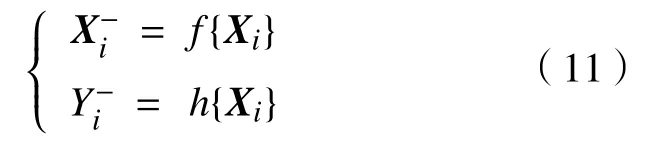
式中,f{·}、h{·}分别表示系统状态方程、观测方程的映射关系,分别为点集Xi的状态预测、系统输出,其中,h{·}是通过查表的方法对观测方程进行准线性化处理.
(2)迭代算式.
假设过程噪声w(k)服从N(0,)分布,观测噪声v(k)服从N(0,)分布.
a)预测更新过程为
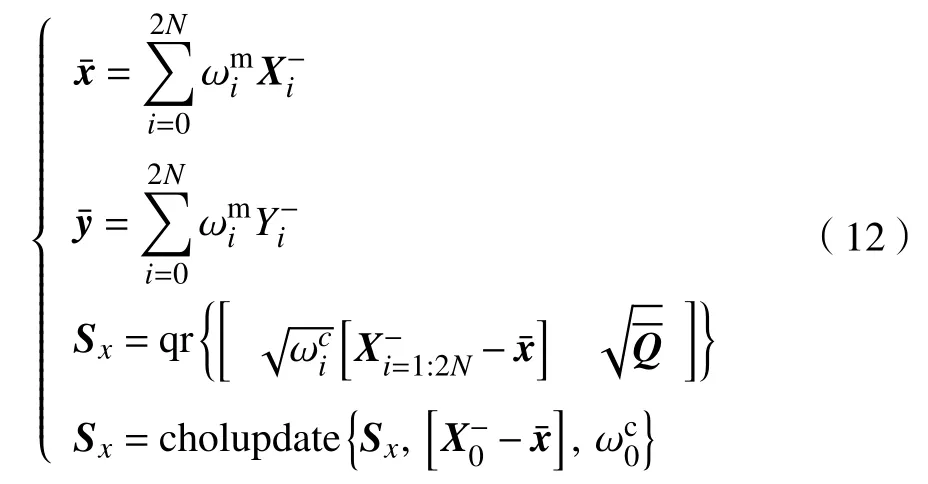
b)观测更新过程为

式中,Z是观测值,G是卡尔曼增益,用于动态调整状态预测与观测残差之间的权重分配,为最优估计结果.
与标准UKF算法相比,本文设计的快速SRUKF算法通过准线性化处理降低了UT变换过程中的计算开销,同时在迭代过程中,用协方差矩阵的平方根代替协方差矩阵,该平方根是由QR分解与Cholesky因子的一阶更新得到,解决了UKF算法迭代过程中可能由计算累积误差引起协方差矩阵负定而导致滤波结果发散的问题,保证了电池SOC在线滚动估计的数值稳定性.
3.1.3 SOC初值校准
工程上,对SOC初值的校准工作是非常有必要的,一则可有效避免估计误差的累积效应,进一步改善估计精度;二则可使估计结果更平滑,且能快速收敛于期望轨迹.
方式1,在电池满充时,将SOC校准为100%;
方式2,长时间静置后,根据当前温度选取相应的OCV-SOC映射表来校准.
3.2 电池SOH估计策略
单体不一致性、监测误差、环境因素等给BMS均衡带来了较大的技术难度,严重时会引起容量低的单体过充过放,进一步加剧了单体之间的不一致性,从而及时了解电池组中各单体的健康状态,并及时更换掉老化的单体,对延长电池组的整体寿命具有实际意义.
随着充放电循环次数的增加,电池欧姆内阻会缓慢增大,电池标称容量也会逐渐衰减,且衰减达20%时电池报废[22].因此,可以通过电池欧姆内阻、电池最大可用容量来间接地表征电池的SOH健康状态.
3.2.1 基于欧姆内阻的SOH估计
与电池SOC估计方法类似,仅需将式(5)所示的模型换成式(8)所示的模型,即可实现欧姆内阻的在线滚动估计.
再利用欧姆内阻对电池SOH进行间接量化,其数学描述[23]为

式中,REOL为电池寿命终结时的阻抗值,R0为电池出厂时的阻抗值.
3.2.2 基于电池容量的SOH估计
车用锂离子动力电池常用恒流转恒压的充电方式,恒流充电时电流恒定,这样安时积分计量法的估算误差较小,可以利用该特点实现对电池总容量的校准.
假设电池t1时刻处于静置状态,St1为t1时刻由开路电压得到的SOC值,St2为恒流充电至t2时刻且静置一段后,由开路电压得到的SOC值.

式中,Qpre为当前电池最大可用容量,为充入电量,其中,I为恒流充电电流.
再利用电池最大可用容量对电池SOH进行间接量化,其数学描述为

式中,Q0为电池出厂时的额定容量.
3.3 电池状态联合估计策略
在实际工程中,考虑到电池老化、温度等因素的影响,有必要对电池等效模型参数Re、Q0进行在线校准,以保证电池SOC的估计精度,而较高的SOC估算精度又将进一步改善SOH估计效果以及BMS管理[24-25].
为此,设计了一种联合估计策略,如图4所示.该策略充分考虑了电池SOC与SOH之间紧密的内在关联性,实时辨识与修正离线标定的电池模型参数,能够较好地解决模型参数的时变问题,保证了电池等效模型的准确性与有效性.同时对SOC初值进行有条件校准,以期避免累积误差,提高收敛速度.
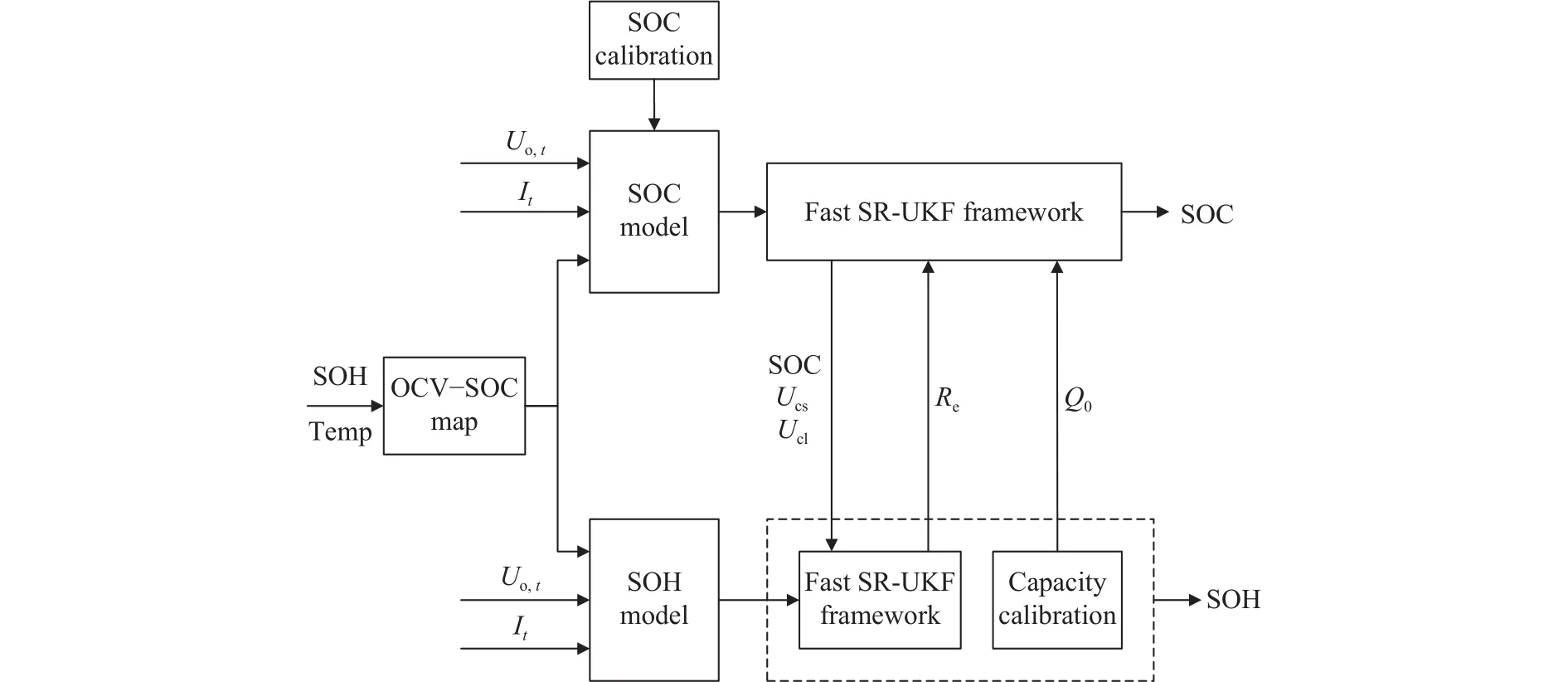
图 4 电池SOC、SOH联合估计策略Fig.4 SOC and SOH co-estimation strategy
4 仿真验证
本文设计的快速联合估计算法记为SR-UKF联合估计,二阶RC网络模型参数的初值见表1,对比实验如下.
(1)SR-UKF联合估计与标准UKF估计对比.
文献[4]表明,锂离子电池的欧姆内阻阻值变化受环境温度以及电池SOC的影响,当环境温度或电池SOC较高时,电池的活性增强,从而欧姆内阻阻值较小,反之亦然.
实验条件:
放电实验过程中,将恒温箱温度由25 ℃缓慢升至30 ℃,采样周期为30 s.
SR-UKF联合估计与标准UKF估计[13]的仿真对比如图5与图6所示.SR-UKF联合估计的最大误差约1.4%,且误差曲线呈收敛趋势,而标准UKF估计误差曲线的收敛性较差,从而SR-UKF联合估计优势相对明显,能够较好地适应电池等效模型参数的时变特性.

图 5 SR-UKF联合估计与标准UKF估计曲线对比Fig.5 Comparison of SR-UKF and UKF estimations
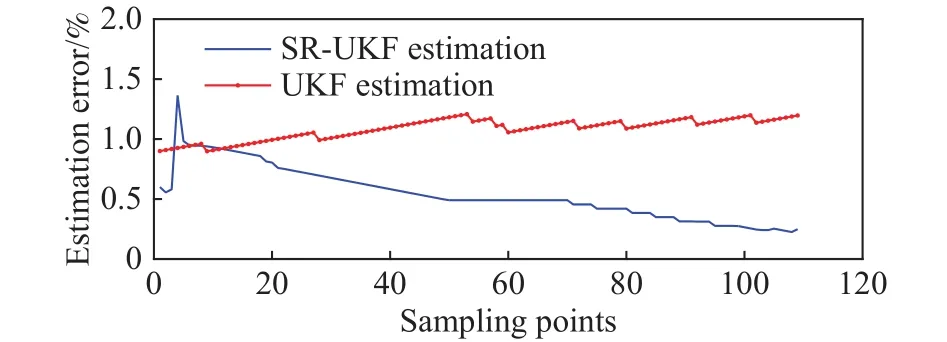
图 6 SR-UKF联合估计与标准UKF估计误差曲线对比Fig.6 Comparison of SR-UKF and UKF estimation errors
(2)估计曲线的收敛性对比.
实验条件:
① 常温环境下,采用恒流放电方式,采样周期为30 s;
② SOC真实值为98%,而初值标定为93%.
如图7所示,在SOC初值标定偏差为5%的情况下,由于AH安时计量法是开环估计,从而滤波过程中AH估计曲线始终不能收敛于期望轨迹,而采用闭环的SR-UKF估计能够较好解决AH估计因SOC初值标定不准而引入的估计误差问题.

图 7 SOC初值标定偏差为5%情况下的SOC估计曲线对比Fig.7 Comparison of SOC estimations when the calibration deviation of initial SOC value is 5%
(3)电池内阻估计.
如图8所示,电池模型参数中欧姆内阻初值标定分别为5和8 mΩ的情况下,经过SR-UKF迭代运算,两条估计曲线的变化趋势几近一致,即由内阻初值偏差而引入的扰动对估计结果的影响并不明显.此外,在电池放电初始阶段,由于电池放电产生的热量,使得内阻阻值出现略微减小的过程,而当电池SOC较低时,内阻阻值显著增大.

图 8 电池内阻估计曲线Fig.8 Comparison of li-ion battery inner resistances
前文中,图2已描述了一个脉冲放电周期内单体端电压的变化过程,在放电瞬间端电压由于欧姆内阻上产生的压降而发生抖降现象.进一步,图9描述的是端电压的峰值与谷值压差变化曲线,当SOC较低后,由于放电过程的端电压下降的幅度将显著高于静置过程的端电压所能回弹的幅度,从而压差曲线呈上升趋势.
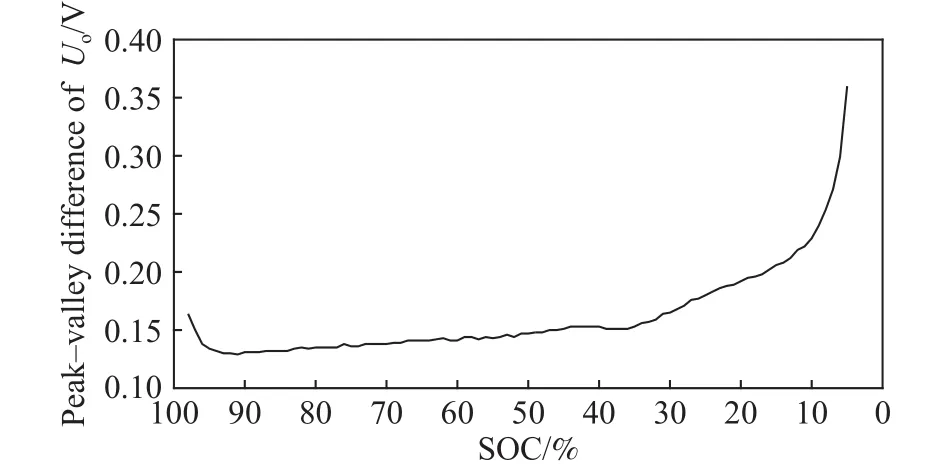
图 9 放电过程中端电压的峰谷压差曲线Fig.9 Peak-valley difference in terminal voltage during discharge process
(4)电池额定容量标定.
由于恒流充电时电流相对恒定,这样安时积分计量法的估算误差较小,再通过式(15)对电池额定容量进行校准,以降低初始估计偏差.
本实验所用电池包中,最低单体电池额定容量Q0的标定结果约为29.3 A·h,说明单体容量已有一定程度的衰减了.为此,基于图4所示的联合估计策略对Q0进行定期在线更新,保证电池等效模型的准确性与有效性是有必要的.
(5)实车工况验证.
实验条件:
① 试验车为安凯纯电动公交车,试验场地在定远国家汽车试验场,单体的标称容量为200 A·h,采样周期为0.5 s,试验车的整个电流工况如图10所示;

图 10 试验车的电流工况Fig.10 Currency curve of test vehicle
② SOC真实值为99%,而初值标定为95%.
如图11所示,在SOC的初值标定偏差为4%的情况下,相比AH估计法,SR-UKF估计曲线能够快速收敛于期望轨迹,实车工况进一步验证了SRUKF估计算法的有效性.
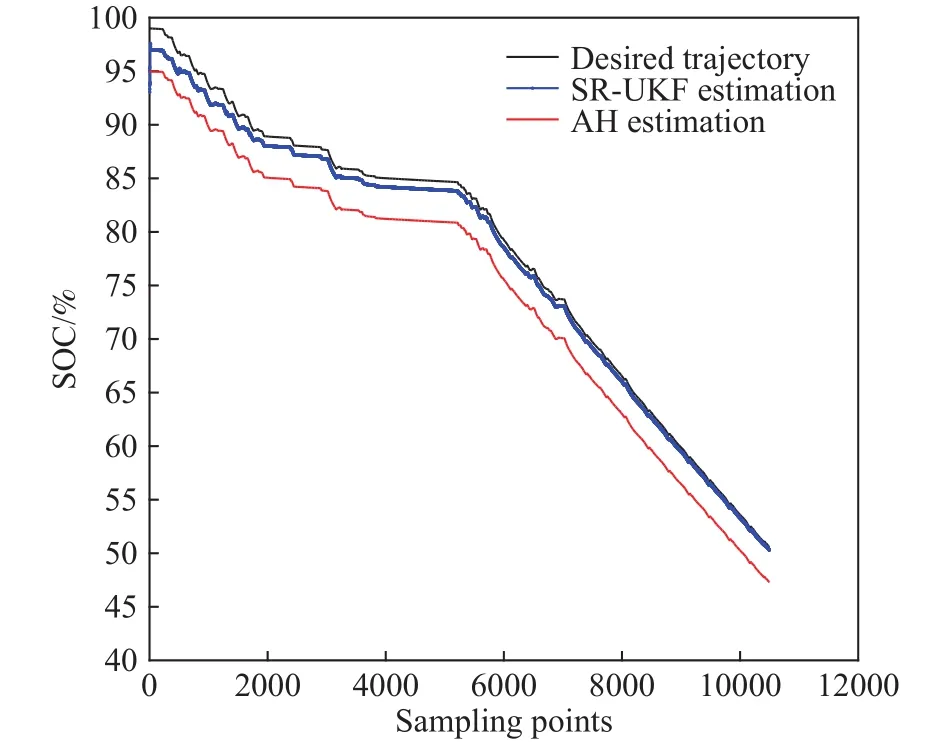
图 11 SOC初值标定偏差为4%情况下的SOC估计曲线对比Fig.11 Comparison of SOC estimations when the calibration deviation of initial SOC value is 4%
5 结论
针对标准UKF算法本身存在着因状态误差协方差矩阵无法实现Cholesky分解而导致滤波发散的隐患,以及在电池状态估计过程中由离线标定的电池等效模型参数而造成的累积误差的问题,本文设计了一种快速SR-UKF算法以及电池状态联合估计策略,主要结论如下.
(1)快速SR-UKF算法通过对观测方程进行准线性化处理,降低了UT变换过程中的计算开销;同时采用闭环设计避免了工程上AH开环估计不能收敛的缺陷.
(2)在SR-UKF迭代过程中,用协方差矩阵的平方根代替协方差矩阵,该平方根是由QR分解与Cholesky因子的一阶更新得到,解决了标准UKF算法迭代过程中可能由计算累积误差引起协方差矩阵负定而导致滤波结果发散的问题,保证了电池SOC在线滚动估计的数值稳定性.
(3)联合估计策略充分考虑了电池SOC、电池容量以及内阻之间紧密的内在关联性,能够较好地适应电池等效模型参数的时变特性,从而提高了电池SOC的估计精度.
