一种适用于小入射角条件下的白冠海面后向散射模型

曲晓俊, 李 晨, 戴永寿

一种适用于小入射角条件下的白冠海面后向散射模型

曲晓俊, 李 晨, 戴永寿

(中国石油大学(华东), 海洋与空间信息学院, 山东 青岛 266580)

本文提出了一种白冠海面的小入射角星载雷达后向散射模型, 模型包括海面非波浪破碎部分和波浪破碎部分的后向散射。在风的作用下, 海浪破碎形成白冠, 对星载雷达的后向散射信号造成影响。文中利用热带降雨测绘任务卫星搭载的降雨雷达(TRMM PR)和欧洲中期天气预报中心(ECMWF)的时空匹配数据集, 拟合得出小入射角下星载雷达海面波浪破碎部分的后向散射模型, 并分别与高斯分布/非高斯的海浪斜率分布海面的准镜面散射模型组成了白冠海面小入射角星载雷达后向散射模型。经实测数据对比, 本文提出的由非高斯准镜面散射和考虑波浪破碎组合模型有效。

白冠海面; 半经验方法; 小入射角; 后向散射模型

在海洋环境中, 海表面在风的连续作用下产生波浪, 波浪逐渐成长, 其波动的非线性增强[1]。当风速达到某一临界值时, 波浪发生破碎并在波峰处产生大量的水沫和水滴, 同时在海水内部和表面产生大量的气泡, 这种在波面上清晰可见的白色水体就是所谓的海洋白冠[2]。随着风速持续增强, 白冠覆盖率达到一定值时, 海洋白冠会显著改变海面的介电性质和辐射特性, 对星载卫星遥感测量产生影响。研究表明, 在微波波段中白冠引起的海面微波辐射率与无白冠海面相比较约增加20%～30%, 其特性显著不同[3]。

对于星载遥感雷达来说, 依据其工作原理不同, 其入射角各异。工作在小入射角下的星载雷达, 海面对其微波信号的作用主要是准镜面散射; 而工作在中等入射角下的雷达, 散射信号以Bragg散射为主。研究海面波浪与雷达散射信号之间的关系, 一般采用物理分析法与经验拟合法两种方法。由于白冠海面对雷达后向散射信号的影响机理较为复杂, 目前大多数采用经验方法对它们进行研究[4-5]。

物理分析法与经验拟合法是两种不同的建模方法。前者通过白冠模型来描述波浪破碎海面的雷达后向散射信号[6], 后者是通过分析大量的实际测量数据建立经验拟合模型。目前使用物理分析法对白冠海面雷达后向散射建模的研究都是针对中等入射角的[6], 对适用于小入射角条件下的白冠海面后向散射物理解析模型的研究较少。Kudryavtsev等[7]在2003年提出中等入射角下的半经验模型, 此模型考虑了海面非波浪破碎部分的Bragg散射对于雷达后向散射的贡献, 也考虑海面波浪破碎部分对雷达后向散射的贡献[7], 但此模型仅适用于中等入射角。

本文利用热带降雨测绘任务卫星搭载的降雨雷达(tropical rainfall measuring mission precipitation radar, TRMM PR)和欧洲中期天气预报中心(European centre for medium-range weather forecasts, ECMWF)的ERA-interim再分析数据集产品进行时空匹配, 获得实测数据集, 拟合得到白冠海面后向散射影响的经验模型。结合海面非波浪破碎部分的准镜面散射模型, 建立了适用于小入射角条件下的半经验白冠海面后向散射模型。

1 数据

本文采用的数据来自于热带降雨测绘任务卫星搭载的降雨雷达TRMM PR的后向散射数据和欧洲中期天气预报中心ECMWF的再分析数据产品。通过对这两者进行时空匹配处理, 得到各风速对应的后向散射数据。

1.1 降雨雷达数据

降雨雷达PR是一种星载Ku波段水平偏振雷达, 其天线是一种电子扫描相控阵, 扫描通过星下点的平面交叉轨迹, 星下点空间分辨率为5.0 km×4.1 km, 宽度为250 km, 从–18°左右到18°有49个入射角, 研究中采用的是其中0°～10°的小入射角数据。为了避免在分析过程中受到降雨对后向散射的影响, 在时空匹配过程中根据降雨标志剔除了降雨时的后向散射数据[8]。

1.2 欧洲中期天气预报中心数据

欧洲中期天气预报中心ECMWF提供了对全球气候进行数字描述的再分析数据集, 可以开放获取并免费下载大量气象数据。其中ERA-Interim再分析数据集的默认空间分辨率是0.75°×0.75°(约80 km), 时间分辨率为6 h, 即按00、06、12、18四个时次分别统计。再分析数据集是根据各个参与国的卫星和地面气象设施综合起来获取分析的数据, 属于由复杂的数学公式计算出来的模式数据, 并同化了雷达和浮标数据, 从而提高了预报的准确性。ERA-Interim再分析月平均资料数据集区域范围覆盖全球(0°E～360°E; 90°S～90°N)。

在本文的研究中, 选用了2014年6月的降雨雷达PR的后向散射数据和ECMWF的风速数据, 通过时空匹配, 获得五个小入射角(2°、4°、6°、8°、10°)的实测数据集, 用于下一步的模型分析和验证。

2 方法与实验

2.1 准镜面后向散射模型

在小入射角情况下, 星载遥感雷达的后向散射机制以准镜面散射为主。Barrick[9]和Valenzuela[10]根据粗糙表面的电磁散射原理得出了小入射角下(0°到15°之间)准镜面散射在后向散射中占主导地位。

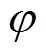
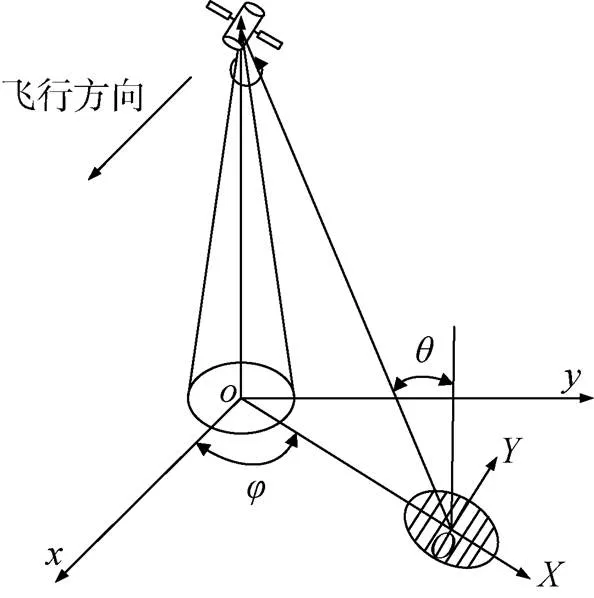
图1 小入射角星载雷达观测几何示意图

在准镜面散射机制下雷达的后向散射可表示为:

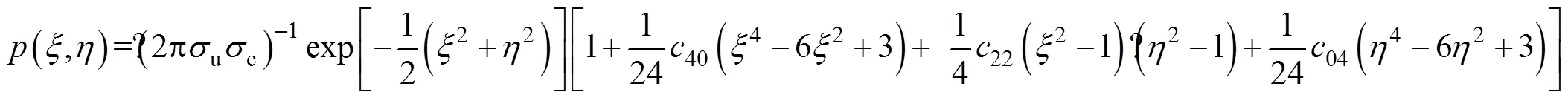
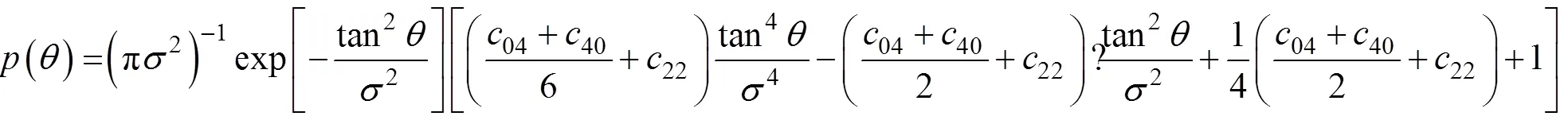
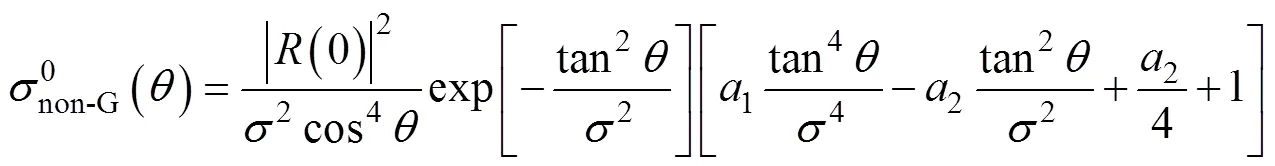
将准镜面后向散射模型(5)的仿真数据与上节中的所介绍的2014年6月匹配实测数据集进行比较。如图2所示, 圆圈点数据表示0°、2°、4°、6°、8°和10°入射角的实测数据集, 点线表示非高斯分布的准镜面后向散射模型的仿真值。在风速较大(风速大于8 m/s)的情况下, 实测数据普遍大于准镜面模型仿真数据; 在入射角为10°时, 实测和仿真数据较为接近。在风速大于8 m/s的情况下, 波浪发生破碎并在波峰处产生大量的水沫和水滴, 在海水内部和表面产生大量的气泡, 形成白冠[2], 对遥感测量产生较大影响, 导致模型仿真值与实测值之间产生偏差。

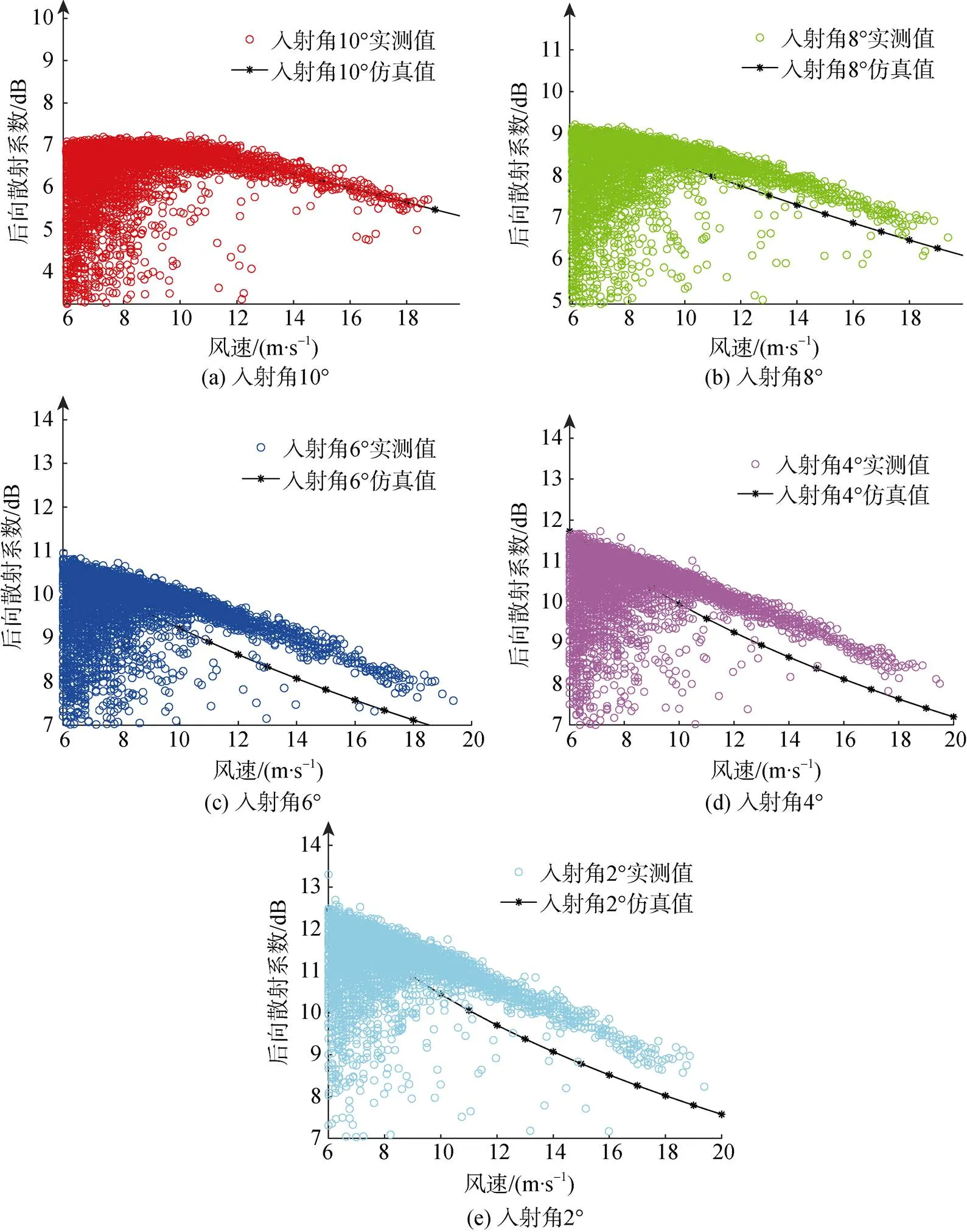
图2 非高斯准镜面散射模型仿真数据与实测数据的比较

2.2 白冠海面后向散射模型

研究白冠海面对雷达电磁波信号的影响, 由于其机理较为复杂, 大多采用经验方法进行研究。Kudryavtsev等提出的半经验模型指出, 海面波浪破碎部分与非波浪破碎部分对雷达后向散射的影响在统计上是相互独立的[7], 其模型表示为:

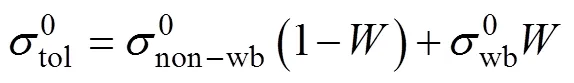
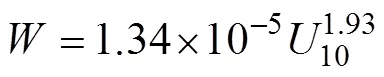
式中,10为海面上方10 m处的风速。

根据式(6), 可以推导出海面破碎部分的后向散射系数为:

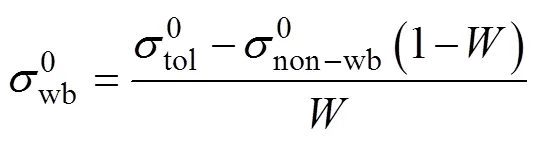
根据式(8), 采用2014年6月的PR降雨雷达后向散射数据减去非高斯准镜面散射模型的仿真数据, 即可得到海面破碎部分的后向散射数据。Li等[14]发现海面波浪破碎部分下的后向散射数据与风速具有相关性, 故这里绘制了入射角范围为2°、4°、6°、8°、10°的后向散射系数随风速的变化关系图。从图3中可以看出, 各个入射角下后向散射系数值随风速表现出相似的变化, 均呈下降趋势。总体而言, 后向散射测量值与风速之间体现了良好的相关性。

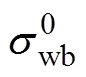
式中, pi (i=1, 2, 3)表示为各阶的拟合系数。拟合结果如表1所示。

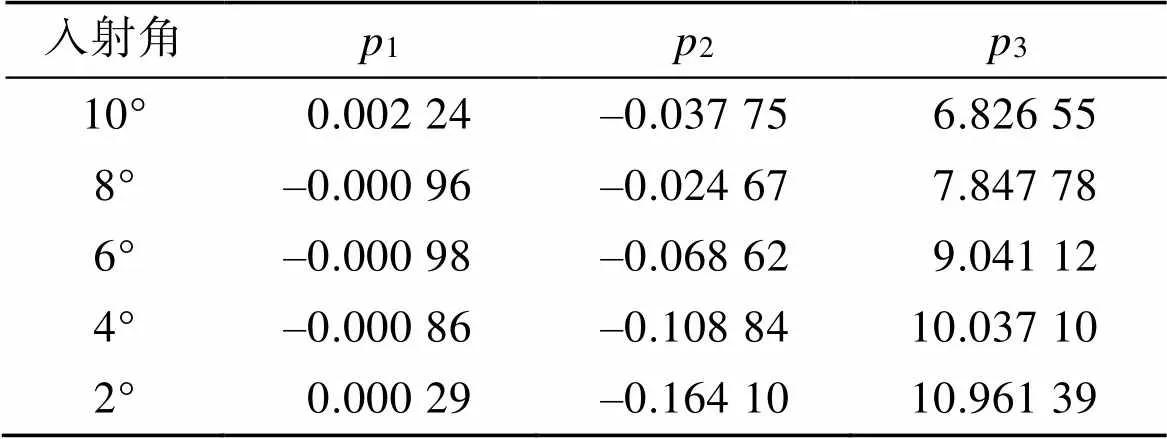
表1 海面波浪破碎部分的后向散射系数与风速的拟合系数表

2.2.1 非高斯白冠后向散射模型

为了分析非高斯分布的海浪斜率情况下后向散射模型的具体参数, 将公式(6)改写为:

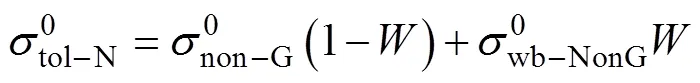
图4展示了模型(10)的仿真值与PR和ECMWF实测匹配数据集的对比图。其中, 星号表示实测数据在各个整数风速处的平均值, 曲线表示模型(10)的仿真值。计算它们的均方根误差与相对误差, 计算公式见式(11), 结果如表2所示, 均方根误差在0.13～0.26, 相对误差在1.1%～3.2%。

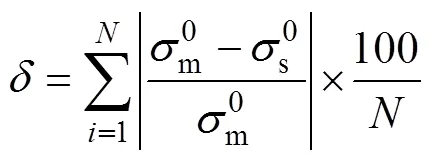
式中, 为PR和ECMWF实测匹配值, 为模型仿真值, N为数据点数量。

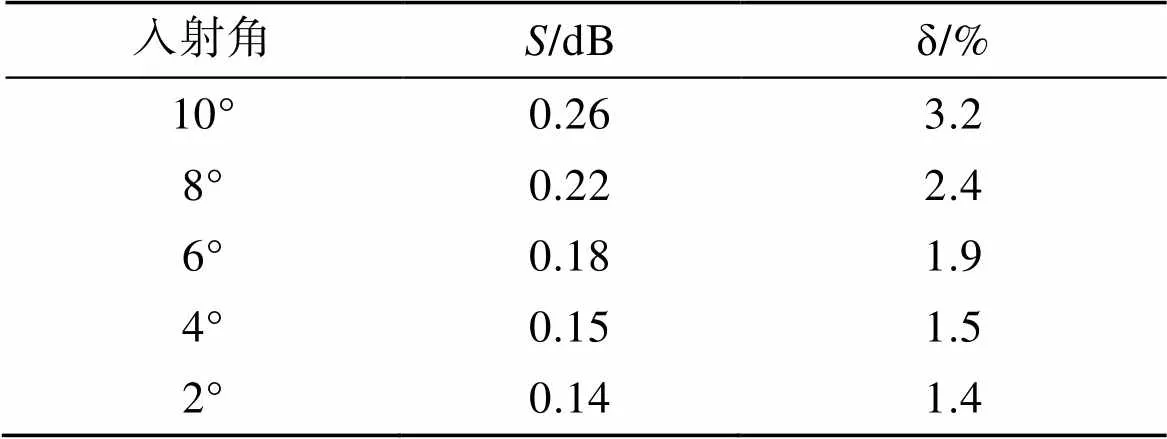
表2 非高斯白冠后向散射模型误差分析表

可以看出, 2°入射角的均方根误差与相对误差最小, 随着入射角增大, 均方根误差与相对误差也随之增加。

2.2.2 高斯白冠后向散射模型

将式(5)中系数1和2设置为零, 则得到高斯分布海浪斜率的准镜面散射模型。为了分析高斯分布的海浪斜率情况下后向散射模型的具体参数, 将公式(6)改写为:

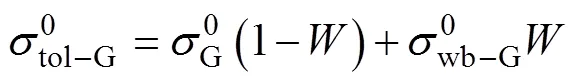
图5显示了模型(12)的仿真值与实测匹配数据集的对比图。其中, 星号表示实测数据在各个整数风速处的平均值, 曲线表示模型(12)的仿真值。计算它们的均方根误差(RMSE)与平均绝对百分误差(MAPE), 结果如表3所示, 其均方根误差在0.20～0.64, 相对误差在1.7%～7.7%。

图5 高斯海浪斜率分布的白冠海面后向散射模型仿真值与实测值的对比

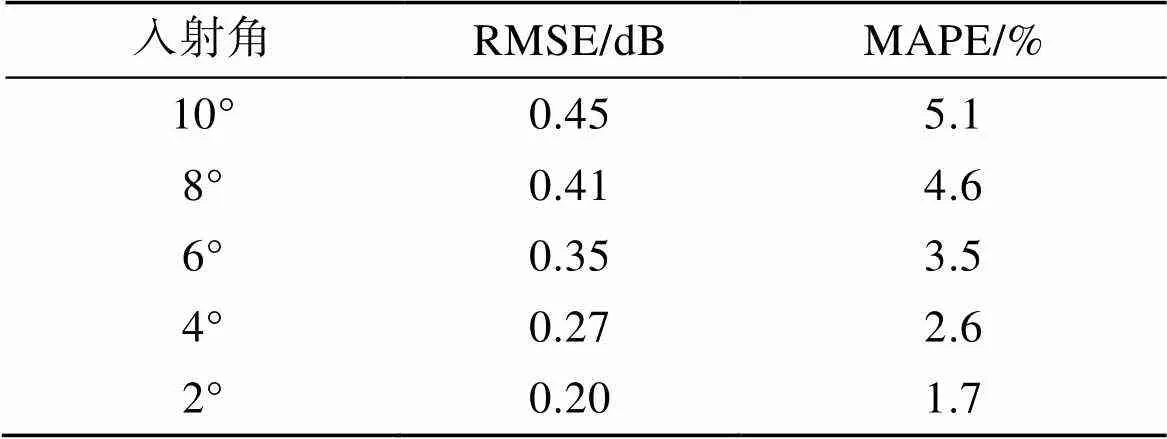
表3 高斯白冠后向散射模型误差分析表

由以上结果可知, 非高斯准镜面散射模型结合海面波浪破碎部分拟合模型的仿真值误差较小, 平均均方根误差为0.19、平均相对误差为2.08%; 高斯准镜面散射模型结合海面波浪破碎部分拟合模型仿真值误差较大, 平均均方根误差为0.38、平均绝对百分误差为4.08%。故非高斯准镜面散射模型结合海面波浪破碎部分拟合模型描述白冠海面的后向散射效果更好。

2.3 模型验证

为了进一步验证非高斯准镜面散射和考虑波浪破碎组合模型的准确性, 这里使用了2014年1月的PR和ECMWF实测匹配数据集来进行验证。如图6所示, 横坐标表示实测匹配数据集, 纵坐标表示利用所建立的模型(10)计算得到的预测值。

为了观察了实测值和预测值的分布情况, 并使结果更加直观, 绘制了45°参考线。当数值在参考线附近时, 表示预测值与实测值接近。如图6所示, 仿真值与实测值一致, 且均方根误差为0.17 dB, 相关系数为0.81。

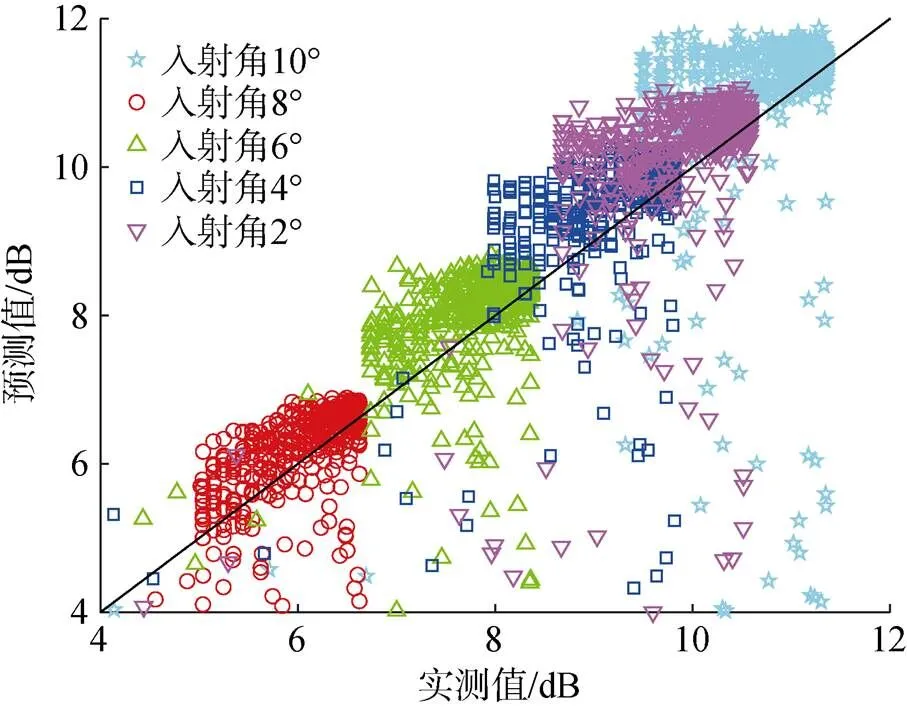
图6 模型仿真值与实测值的比较

3 结论

本文针对白冠海条件下的海面, 利用降雨雷达PR的后向散射数据匹配ECMWF的风速数据作为数据源, 采用半经验方法得到了海面波浪破碎部分的拟合模型, 结合准镜面散射模型提出了一种白冠海面的小入射角后向散射模型, 通过实测数据验证了该模型的准确性。

[1] 刘淑波. 泡沫覆盖海面微波辐射机理研究[D]. 青岛: 中国科学院海洋研究所, 2015.

Liu Shubo. Research for the microwave radiation mechanism of foam-covered sea surface[D]. Qingdao: Institute of Oceanology, China Academy of Sciences, 2015.

[2] 于婷. 由卫星资料反演全球白冠覆盖率的初步研究[D]. 青岛: 中国海洋大学, 2008.

Yu Ting. The preliminary study of whitecap coverage estimated from routine satellite measurements over the global ocean[D]. Qingdao: Ocean University of China, 2008.

[3] 林风. 粗糙海面电磁波散射与杂波特性分析[D]. 西安: 西安电子科技大学, 2007.

Lin Feng. Analysis of characteristics of electromagnetic wave scattering and clutter from rough ocean sur­face[D]. Xi’an: Xi’an University of Electronic Science and Technology, 2007.

[4] Freilich M H, Vanhoff B A. The relationship between winds, surface roughness, and radar backscatter at Low incidence angles from TRMM precipitation radar measurements[J]. Journal of Atmospheric & Oceanic Technology, 2003, 20(4): 549-562.

[5] Li X, He Y, Zhang B. Ku-Band sea surface radar backscatter at low incidence angles under extreme wind conditions[J]. IEEE Transactions on Geoscience & Remote Sensing, 2017, 7(3/4): 537-550.

[6] 田纪伟, 曹红杰, 覃正. 海浪破碎对海面微波后向散射系数的影响[J]. 中国科学(D辑), 2001, 31(4): 342-352.

Tian Jiwei, Cao Hongjie, Qin Zheng. Effect of wave breaking on microwave backscattering coefficient of sea surface[J]. Chinese Science (Series D), 2001, 31(4): 342-352.

[7] KUDRYAVTSEV V, HAUSER D, GAUDAL G, et al. A semiempirical model of the normalized radar cross- section of the sea surface 1. Background model[J]. Journal of Geophysical Research Oceans, 2003, 108(C3): 8054.

[8] Li X, He Y, Zhang B. Simulation and retrieval of CFOSAT at whitecap sea[C]. IEEE International Geoscience and Remote Sensing Symposium, 2016: 5808- 5811.

[9] Barrick D E. Correction to rough surface scattering based on the specular point theory[J]. IRE Transactions on Antennas and Propagation, 1969, 17(1): 81.

[10] Valenzuela G R. Theories for the interaction of electromagnetic and oceanic waves-A review[J]. Boundary-Layer Meteorology, 1978, 13(1/4): 61-85.

[11] Cox C, Munk W. Slopes of the sea surface deduced from photographs of sun glitter[J]. Bulletin of the Scrip­ps Institution of Oceanography, 1956, 6 (9): 401-488.

[12] 王伟, 徐德伦, 楼顺里, 等. 海面阻力系数与白浪覆盖率的关系[J]. 海洋与湖沼, 1990, 21(6): 516-521.

Wang Wei, Xu Delun, Lou Shunli, et al. Relationship between drag coefficient of sea surface and whitecap coverage[J]. Oceanologia et Limnologia Sinica[J], 1990, 21(6): 516-521.

[13] Monahan E C, Muircheartaigh I ó. Optimal power-law description of oceanic whitecap coverage dependence on wind speed[J]. Journal of Physical Oceanography, 1980, 10(12): 2094-2099.

[14] Li X, He Y, Zhang B, et al. A geometrical optics model based on the non-Gaussian probability density distribution of sea surface slopes for wind speed retrieval at low incidence angles[J]. International Journal of Remote Sensing, 2016, 37(3/4): 537-550.

Whitecap sea surface backscattering model for low incidence angles

QU Xiao-jun, LI Chen, DAI Yong-shou

(College of Oceanography and Space Informatics, China University of Petroleum, Qingdao 266580, China)

This study presents a spaceborne radar backscattering model of a whitecap sea surface under low incidence angles, which includes the backscatters of the non-wave-breaking region and the wave-breaking region of the sea surface. With wind, the broken waves form whitecaps, which affect the backscattering signal of the spaceborne radar. The backscattering model of the sea surface wave-breaking region of the spaceborne radar under low incidence angles is fitted based on the space-time collocating datasets of tropical rainfall measuring mission precipitation radar (TRMM PR) and European centre for medium-range weather forecasts (ECMWF). The whitecap sea surface spaceborne radar backscattering model is formed by comparing it with the quasi-specular scattering model under the Gaussian/non-Gaussian probability density distribution of sea surface slopes at low incidence angles. Compared with the measured data, the combined model of non-Gaussian quasi-specular scattering and wave breaking proposed in this paper is found to be effective.

whitecap sea surface; semi-empirical method; low incidence angles; backscattering models

Nov. 7, 2020

TP722.6

A

1000-3096(2021)05-0002-07

10.11759/hykx20201107002

2020-11-07;

2020-12-24

国家重点研发计划项目(2017YFC1405600); 中央高校基本科研业务费专项资金资助(17CX02079)

[National Key Research and Development Program of China, No. 2017YFC1405600; The Fundamental Research Funds for the Central Universities, No. 17CX02079]

曲晓俊(1978—), 男, 山东莱州人, 博士, 研究方向: 海洋遥感, E-mail: xjqu@upc.edu.cn; 李晨(1995—),通信作者, 男, 山东莱芜人, 硕士研究生, 主要从事信号检测与处理研究, E-mail: lc1730508315@ 163.com

(本文编辑: 赵卫红)