植被异质性样区真实性检验的优化采样策略

李若溪，周 翔，吕婷婷，陶 醉，王 锦，谢富泰

植被异质性样区真实性检验的优化采样策略

李若溪1,2,3，周 翔1※，吕婷婷1，陶 醉1，王 锦1，谢富泰1,2,3

（1. 中国科学院空天信息创新研究院，北京 100101；2. 中国科学院大学，北京 100049；3. 中国科学院大学电子电气与通信工程学院，北京 100049）

遥感反演植被产品的真实性检验是推动其在农业领域应用水平提升的重要保证，其中异质性植被样区的优化采样设计是真实性检验地面测量过程中的关键技术。该研究以遥感影像作为先验知识，通过K-means聚类分层选取初始样点，利用空间模拟退火算法规划最优采样方案，并采用同期地面实测数据进行检验。研究结果表明，空间模拟退火算法在样点与总体空间变异性的一致性、插值面的精度、插值点和实测点的相关性3个方面都明显优于传统采样方案，2块样区优化后的采样方案插值面与影像面的均方根误差分别为3.102 6和2.962 7，插值点与实测点的皮尔逊相关系数分别为0.601和0.757，表明空间模拟退火算法可以为真实性检验地面试验提供可靠的优化采样策略。

遥感；算法；采样；真实性检验；植被异质性样区

0 引 言

农业是支撑国民经济的一大重要产业，随着遥感技术的快速发展，遥感数据在农用地资源调查、农作物长势监测、农作物估产和农业气象灾害预测等领域得到广泛应用[1]。近几年来基于不同传感器、不同空间尺度、不同反演算法的遥感植被产品越来越多，例如由星上自主项目-植被卫星（Project for On-Board Autonomy Vegetation，PROBA-V）、哨兵3号（Sentinel-3）卫星数据生产的空间分辨率为300 m的全球时间序列植被产品；由美国海洋大气管理局（National Oceanic Atmospheric Administration，NOAA）气象观测卫星搭载的高分辨率辐射仪（Advanced Very High Resolution Radiometer，AVHRR）生产的全球公里级植被类产品；基于美国宇航局泰拉（Terra）卫星搭载的中分辨率成像光谱仪（Moderate-Resolution Imaging Spectroradiometer，MODIS）数据生产的250、500和1 000 m的全球植被产品等。这些植被产品广泛应用于农作物熟制分布[2]、农田干旱监测[3]、农田覆盖变化[4]、植被物候[5]等诸多研究领域，为农业生产提供了数字化、定量化和机理化的支撑[6]，成为宏观快速监测区域或全球尺度植被生长状态的有效手段。不同的植被产品之间存在差异，差异的来源除了传感器不同之外，还与数据的预处理、生产算法的不同有关。因此科学地评价植被产品精度及不确定性是准确使用这些数据的重要基础。

遥感产品真实性检验是指通过与参考数据（相对真值）比较，独立地评价遥感产品精度和不确定性的过程，是评价遥感产品质量、可靠性和适用性的唯一手段[7]。目前，遥感反演植被产品的真实性检验主要分为间接检验和直接检验两种方法。间接检验是利用精度已知的同类产品作为参考对待检验产品进行评估的方法，该方法仅能给出待检验产品和参考产品间的相对准确度和不确定度。直接检验是利用地面测量数据对遥感产品进行检验和评估的方法，该方法是遥感产品真实性检验的主要方法。虽然真实性检验工作已经取得了很大的进展，但由于地表空间异质性的普遍存在[8-9]，异质性地表遥感植被产品的真实性检验仍面临很大的挑战。对于中低分辨率的遥感植被产品来说，获得像元尺度的地面观测相对真值是真实性检验的核心问题。如果像元内对应地物均一，通常可以忽略异质性的影响，可将地面观测值与待检验产品像元值直接比较开展精度评价。但在实际验证工作中发现，由于作物长势的差异以及多种地物类型的存在，中低分辨率的植被产品在像元尺度的地表通常具有空间异质性，因此需要测量大量的地面样点，来捕捉地表的空间变异，才能代表像元范围内植被参数的相对真值。对于高分辨率遥感植被产品而言，由于像元尺度地表内的异质性可以忽略，获取待检验产品范围内具有空间代表性的样点是真实性检验的关键。

在异质性样区数据采集的过程中，采样点的随机性或样点数量的不足会导致不可接受的采样误差，从而错误地评估卫星产品的精度。高密度采样可以避免采样随机性引起的采样误差[10]，但需消耗大量的人力、财力。因此如何在研究范围内确定最少样点的最优位置，使其具有最佳的全局代表性是优化采样策略需要解决的重要问题。目前植被类遥感产品真实性检验过程中常用到的样点空间布设方法主要有：空间简单随机采样、空间系统采样、空间分层采样和样区内固定的正方形、交叉和样带采样模式等[11]。这些采样方法均是以植被特征状态的空间变异是随机的、样本完全独立且服从某类型的概率分布作为假设前提，而没有考虑到植被参数的空间相关性和样点的空间位置。而事实上不同尺度上的植被均呈现出一定的空间结构，且具有明显的空间相关性。如果采用这些方法会导致局部样点冗余或局部样点不足的情况。因此许多采样方法从单纯的统计采样发展到考虑空间相关性的采样[12-14]。样点的确定方法也从单纯的“找点”再评估变成将评价指标作为目标函数，寻找最优解的过程。随着采样区域以及样本量的增大，一些广泛使用的高效算法也被应用到空间样点优化中，如空间模拟退火算法[15]、神经网络[15]、遗传算法[16]和蚁群算法[17]等。这些智能优化算法的引入本质都是模拟一种常见的生物、物理、化学现象，不断搜索、变异、扰动产生新解，从而实现样本的优化组合，非常适合大样本量的最优解的计算。

综上，本研究以异质性植被样区作为采样策略设计对象，采用同期遥感影像提取的能有效反应地表植被类型及生长状况的归一化植被指数（Normalized Deference Vegetation Index，NDVI）[18-20]作为先验知识，通过分层采样生成最初的样点布局。然后以克里金方差最小作为目标函数，通过空间模拟退火算法实现初始样点的优化布局，并对布局方案的可靠性进行评价。以期为植被遥感产品的真实性检验提供可靠的精度评价，进而推动遥感植被产品更好地应用于农业研究。

1 材料与方法

1.1 数据来源及预处理

本研究开展采样策略优化的试验样区位于河北省北部张家口市坝上地区的沽源县，是内蒙古高原向华北平原过渡的地带，属温带大陆性草原气候。本研究样区选择的基本原则为1）植被样区具有明显的异质性；2）交通方便，便于实测；3）样区空间范围300 m×300 m。根据以上要求选出2块具有代表性的样区，每个样区采样数量均为50个。1号样区（41°45′51.12″N～41°45′41.53″N，115°40′43.38″E～115°40′56.99″E）的植被以马铃薯为主，由于地面试验日期为2018年7月29日至8月1日，正值马铃薯生长中后期。2号样区（41°42′37.26″N～41°42′47.05″N，115°43′56.83″E～115°44′10.59″E）的植被以羊草为主。2块样区的空间位置和地表实测点的空间分布如图1所示。

本研究选取2018年8月1日覆盖试验区的Sentinel-2A卫星数据来计算NDVI。首先利用欧洲空间局发布的针对哨兵卫星数据的Sen2Cor软件对其进行大气校正，然后利用红波段（Sentinel-2A的第4波段）和近红外波段（Sentinel-2A的第8波段）的反射率数据计算NDVI，计算如式（1）所示

地面测量NDVI通过美国ASD（Analytica Spectra Devices.，Inc）公司生产的便携式地物光谱仪的测量数据计算获取。由于ASD地物光谱仪的光谱测量范围在350～2 500 nm之间，所以首先要根据Sentinel-2A卫星传感器光谱响应函数对测量光谱通过卷积运算进行光谱等效，其计算如式（2）所示

本研究2块样区的NDVI实测点数分别为49个和78个，与遥感影像对应位置像元值的皮尔逊相关系数分别为0.85和0.89。

1.2 研究方法

本研究以异质性植被区域作为对象开展采样策略优化设计，主要步骤包括1）将基于遥感影像的NDVI产品作为先验知识引入采样设计。2）基于选定的先验知识，采用变异函数和NDVI频率分布直方图开展样区异质性评价，实现空间分层采样。3）在分层采样确定的初始样点的基础上使用空间模拟退火（Spatial Simulated Annealing，SSA）算法，以平均克里金方差最小作为目标函数实现样点的布局优化。4）建立不同采样数量与预测误差之间的关系，在考虑采样成本的情况下确定合理采样数量。5）从样点与总体空间变异性的一致性、预测面的精度、插值和实测值的相关性三个方面对采样策略进行评价。具体的技术路线如图2所示。

1.2.1 样区空间异质性评价

1）变异函数法

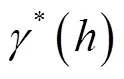
式中为距离间隔，m；()为处的区域化变量，(+)为+处的区域化变量，该区域变化量在本研究中为像元的NDVI；()为间隔距离的个数。

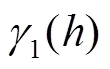
式中为变程，m；0为块金值；为拟合变异曲线稳定时的函数值；0+为拟合变异曲线基台值。块金值为间隔为0时的变异函数值，代表了一种由非采样间隔所造成的变异，理论为0，但是由于测量误差的存在或者观测尺度大于空间变异的细微尺度时，块金值就不为0。变程为半变异函数曲线首次呈现水平状态的距离，描述的区域变量具备空间关联的范围。在变程值以内区域变量具有空间相关性，而在变程值以外这种相关性就会消失。基台值为变异函数的极大值，代表区域变量总的变异程度。块金和基台的比值，又称基底效应，可以用来说明空间的变异特征。该值越大说明空间变异更多是由于随机成分引起，否则是由特定地理过程或多个过程综合引起的。

2）数据正态分布检验

应用克里金方法的一个重要前提是样本数据必须符合正态分布[23]，否则会对变异函数的拟合产生影响。本研究选用柯尔莫可洛夫-斯米洛夫（Kolmogorov-Smirnov，K-S）检验方法对样区数据进行正态分布检验，计算如式（6）所示

1.2.2 样区分层

本研究首先基于样区NDVI数据，通过分层采样方法确定最初的样点布局，为之后的优化提供初始输入。其中分层方法采用K-means聚类分层。分层层数采用聚类评价指标（Calinski-Harabasz，CH）来确定。该指数表征类内紧密度和类间分离度，值越大代表类自身越紧密，类与类之间越分散，计算如式（7）所示

1.2.3 基于地统计学的优化采样策略

本研究在利用变异函数描述区域变量空间变异规律的基础上构建目标函数，通过优化组合算法实现目标函数的最优值，从而确定最优采样点的空间位置。

1）目标函数的建立

本研究选择克里金方差最小作为优化算法的目标函数。克里金法是一种典型的地统计方法[24]，其不仅考虑了各样本数据的空间相关性，而且在给出估计的属性值的同时，还能给出表示估计误差的方差。待估算点的属性值的计算如式（8）所示

2）空间最优组合算法

模拟退火算法是一种随机计算基数，可以有效避免局部最优的算法[25]，因此空间模拟退火算法对于处理组合优化问题有其显著的优势，被广泛应用到空间统计[26]和地统计分析中[27]。目前有些研究利用模拟退火算法进行植被样区的优化采样[28-30]，研究结果表明采用模拟退火优化后的采样方案比简单的随机抽样和系统抽样更能代表整个植被研究区特征[31]。其基本步骤如下：

步骤1：设置初始温度（0，℃）和循环次数。

步骤3：步骤2循环次后，利用降温系数不断降低温度，当温度低于设定截止温度时，充分迭代收敛，实现目标样点的最优布局。

1.2.4 评价方法

本研究中评价采样精度采用的统计分析指标为均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE），计算如式（12）和式（13）所示：

2 结果与分析

2.1 样区的异质性评价

NDVI对植被的生长状态和空间分布密度反映敏感，常用来评价植被地表的空间异质性[32-33]。因此通过最优模型拟合样区NDVI的半方差函数与步距的变异曲线，可以定量分析该区域植被的异质性特征。

对样区NDVI进行变异函数分析之前需要确保样区数据的正态分布，因此本研究分别对2块样区绘制了频率分布图并开展了K-S检验。1号样区NDVI整体分布范围为0.45～0.88，平均值为0.68，高频集中在0.6～0.7之间，偏度较小，峰度平缓，其K-S检验的>0.05，因此整体符合正态分布。2号样区NDVI整体分布范围为0.43～0.86，平均值为0.63，高频集中在0.55附近，正向偏移程度较大，其K-S检验的<0.05，不满足正态分布假设，因此本研究对其进行了对数正态转换处理。

对2块样区的NDVI变量分别采用球状模型、高斯模型方法拟合后得到的特征参数如表1所示，用来描述区域化变量的变异程度。块基比表示随机因素引起的NDVI空间变异，由表1可知，2块样区的块基比（即随机因素引起的空间变异占比）分别为0.182和0.244。随机因素和空间结构共同影响着空间变异，即二者相加为1，因此空间结构引起的空间变异占比分别为0.818和0.756。2块样区的变程值分别为143.7 m和112.9 m，说明大于该距离的NDVI变量将不存在空间自相关性。

表1 样区空间异质性的特征参数

2.2 样区分层及初始点的选取

分层采样是将样本总体按照某种属性分为若干层，然后在各个层内抽取样本点。研究表明通过合理分层抽取出的样点更具有代表性，能够有效提高采样精度[34]。本研究利用CH指标评价聚类结果得出2块样区最佳分类数均为3层，然后对每一个样区进行K-means聚类分层。在样本数量固定的情况下，每一层的样本数量通过该层像元数占总像元数的比例来确定，每一层样点的空间位置通过随机采样的方法来确定。

2.3 空间模拟退火算法优化采样

基于分层的空间采样不能达到全局最优，因此本研究继续在分层采样的基础上使用SSA算法，通过平均克里金方差最小准则[35-40]实现样点的最优布局。SSA算法存在一个很大的问题在于最优解的产生依赖于模型初始参数。为研究各参数设置对采样结果的影响，本研究以克里金方差最小化为准则，通过模拟试验研究不同参数设置对采样精度的影响。结果得出降温系数对采样结果的影响最大，经反复验证本研究将SSA算法的初始温度设置为5 000 ℃，降温系数为0.999。另外，状态的搜索、跳转策略直接影响着算法的性能。扰动采样是经典蒙特卡罗和网格结构采样的混合[41]，因此本研究在SSA算法内循环中设置了扰动边界，使状态转换在边界范围内进行，逐点抖动，同时将每次迭代后的当前最优解作为下一次抖动的起点。此外，接受恶化的概率直接影响算法恶化的程度，本研究接受恶化的初始概率被设置为0.2，并随着迭代的进行呈指数下降。当标准在超过2 000次迭代后没有改进，或迭代次数超过20 000次，SSA算法过程被停止。这意味着采样点从分层采样确定的初始位置在不断地组合变化，最终得到了使克里金方差为最小的最优解。1号样区采样50个点时SSA算法迭代次数和克里金方差的关系如图3所示。

2.4 合理采样点数的确定

在实际采样过程中不存在绝对最优的样本容量，只能在权衡真实性检验过程中采样精度与采样成本后确定合理的采样数量。统计采样中通常采用Cochran公式[42]计算给定置信区间和一定误差要求下的最佳采样数量，例如，本研究2块样区在95%置信水平，5%总体相对误差条件下，最少采样个数分别为24个（1号样区）和22个（2号样区）。但Cochran公式[42]没有考虑实地样区植被空间变异情况，可能会造成不可接受的预测误差和不确定性。本研究利用SSA算法、分层采样和随机采样的方法，选取10～500之间的样点个数，通过建立不同采样数量与克里金预测误差之间的关系（图4），在考虑采样成本的情况下确定合理采样数量。由图4可以判断出不同采样数量对预测误差影响较大，随着样点数量的增加，克里金预测误差逐渐降低，不同采样方法的差距也逐渐缩小。当样点数量足够大时，不同采样方法得到的预测误差同时趋于收敛。由图4可知，SSA算法的优势在于：1）预测精度明显提高。SSA算法优化后的采样点克里金方差比传统采样点误差降低了3～4个数量级。在相同采样数量的条件下，2块样区随机采样得到的预测误差平均是SSA算法的6.4倍和8.1倍，分层采样得到的预测误差平均是SSA算法的3.6倍和2.6倍，说明SSA算法在不同采样数量下均有稳定的优势，能够给真实性检验的提供可靠的代表性强的采样方案。2）采样数量明显减少。在相同预测精度的条件下，2块样区随机采样所需的采样数量约是SSA算法的10倍，分层采样所需的样点数量约是SSA算法的6倍和4.25倍，表明空间模拟退火算法可以在保证精度的情况下，有效地减少真实性检验实地测量的采样成本。3）优化速度明显提高，受采样数影响明显减小。随机采样和分层采样的预测方差随采样个数增加急速下降，直至100个样本量时出现下降拐点，下降速度变缓。此过程说明随机采样和分层采样的结果受样本量影响较大，即采样结果依赖于样本量的合理性，采样精度受采样成本的制约更强。由于SSA算法具有突出的寻找最优解的优势，因此在样本量较少时，也能找到较低预测误差的采样组合，相比之下，对样本量或者采样成本的依赖明显减小。基于上述SSA算法的优势确定，综合考虑置信水平、真实性检验的精度要求、样区范围大小以及采样成本，总样本量被设置为50个。

2.5 采样结果及精度评价

本研究对目前常用的随机采样、系统采样、阈值分割采样与本研究提出的基于先验知识的SSA算法采样策略进行比较，并从三个方面开展采样精度评价来证明SSA算法采样方案的可靠性和高效性。不同方案的样点布局如图5所示。

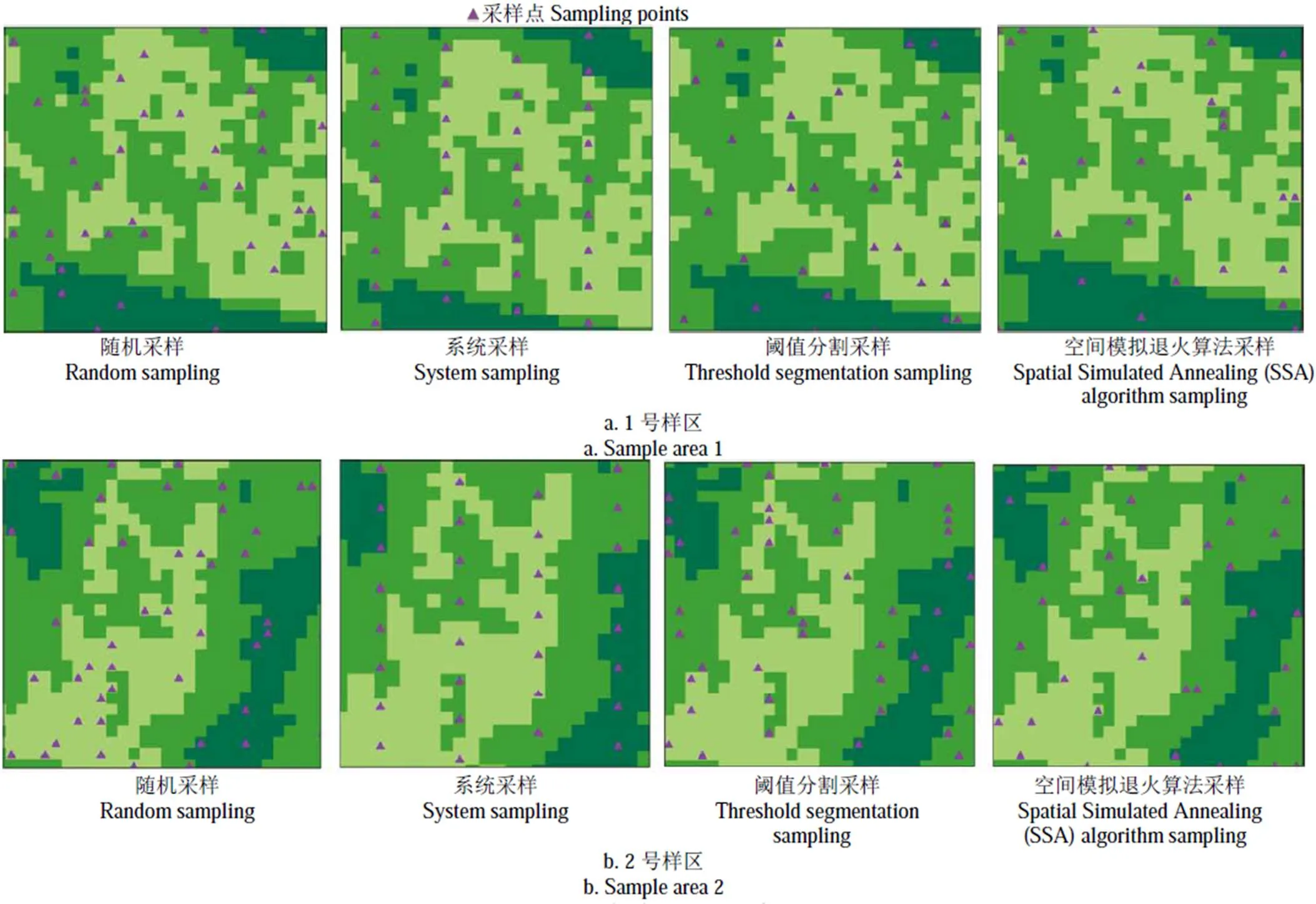
图5 采样点布设方案

2.5.1 基于空间异质性的样点精度评价

基于地统计评价样本点代表性，采样点变异函数与总体变异函数的偏差可以表征样本点模拟抽样总体的能力。与传统采样点相比，基于SSA算法优化后的采样点拟合的变异函数与总体变异函数特征值更接近（图6），2块样区的变程分别为143.7 m和111.9 m，SSA插值面的变程分别为150.9 m和112.9 m，平均变程偏差为3%，而随机采样、系统采样和阈值分割采样的插值面平均变程偏差分别为14%、13%和9%，由此可知，SSA插值面的变程偏差明显减小；2块样区的基台值分别为0.007 5和0.003 8，SSA插值面的基台值分别为0.006 0和0.005 2，平均基台值偏差为28%，而随机采样、系统采样和阈值分割采样的插值面平均基台值偏差分别为63%、30%和35%，由此可知，SSA插值面的基台值偏差明显减小。在一定程度上反映出SSA算法优化后的采样点对抽样总体的模拟能力更好，即在样点本身与总体的关系上证明了SSA算法采样点的代表性。

2.5.2 基于克里金插值面的样点精度评价

基于地质统计学模型的采样通常选择克里金方差最小作为最佳样本的选择标准[43]。插值表面的整体克里金方差可以用来说明插值表面生成的精度，其与样本点的布局息息相关，可以有效规范采样点在空间的合理布局[10]。克里金预测误差表征采样代表性，以遥感影像为基准选出的样点预测面与影像面相关性越高，预测误差越小，平均绝对误差越小，代表性越高。基于克里金插值结果的分析从采样点克里金方差、插值面预测误差和预测相关性3个方面评价，评价结果如表3所示。由克里金方差可知，2块样区基于SSA优化后的采样方案克里金方差分别为0.000 6和0.000 8，明显低于其他采样方案，说明SSA算法采样能充分迭代寻找最佳拟合的采样点，在一定程度上反映了SSA采样策略的可靠性。采样点克里金插值面与影像面的RMSE和皮尔逊相关系数表征采样点对影像的代表性，即模拟还原相对真实地表的能力。2块样区基于SSA采样方案的插值面与影像面的RMSE分别为3.102 6和2.962 7，皮尔逊相关系数分别为0.45和0.73，与其他3种采样方案相比，RMSE最小且皮尔逊相关系数最高。与随机采样、系统采样和阈值分割采样相比，SSA采样方案的插值面与影像面的RMSE分别减少了11%、5%和6%，皮尔逊相关系数分别提高了29%、30%和6%，在一定程度上肯定了采样点的可靠性和代表性。

表3 不同采样方案的克里金插值面精度评价

2.5.3 基于实测数据的样点精度评价

基于实测数据的评价以实测点及其对应位置的基于采样点的插值面为对象，从相关性和MAE两个方面进行采样策略精度评价（表4）。4种采样方案的实测点与插值点的MAE均大于影像点与插值点的MAE，符合地面验证的精度要求，说明对比结果是有效的。2块样区基于SSA采样方案的插值点与实测点的皮尔逊相关系数分别为0.601和0.757，均高于其他3种采样方案；实测点与插值点的MAE分别为0.070 1和0.058 4，影像点与插值点的MAE分别为0.056 8和0.044 1，均低于其他3种采样方案。与随机采样、系统采样和阈值分割采样相比，SSA采样方案的实测点与插值点皮尔逊相关系数分别提高了0.23，0.14和0.07，MAE分别降低了18%、17%和20%，SSA明显优于传统采样方案。

表4 基于实测样点的采样方案评价

3 结 论

以减少采样费用、提高采样效率和精度为目标，本研究针对植被遥感产品真实性检验中异质性样区的采样提出了一种基于先验知识的、以克里金方差最小作为目标函数的空间模拟退火（Spatial Simulated Annealing，SSA）算法优化采样策略，并在试验样区进行了验证。结果表明，由于传统采样方法没有考虑异质性地表的空间自相关性，空间采样不能达到全局最优。本研究提出的结合地统计学和空间模拟退火算法的采样策略能够在保证采样精度的条件下，在2块样区中分别选取最具空间代表性的50个样点，试验表明可以为真实性检验地面试验提供可靠高效的优化采样策略。具体结果如下：

1）从变异函数的特征值来看，本研究方法得到的采样点对抽样总体的模拟能力更好；

2）从克里金插值的角度来看，本研究方法得到的优化采样点的克里金方差比传统采样点误差降低了3～4个数量级。2块样区基于SSA采样方案的插值面与影像面的均方根误差分别为3.102 6和2.962 7，皮尔逊相关系数分别为0.45和0.73，与其他3种采样方案相比，均方根误差最小且皮尔逊相关系数最高。相比随机采样、系统采样和阈值分割采样，SSA采样方案的插值面与影像面的相关性分别提高了29%、30%和6%。

3）从实测数据检验的角度，2块样区基于SSA采样方案的插值点与实测点的皮尔逊相关系数分别为0.601和0.757，实测点与插值点的平均绝对误差分别为0.070 1和0.058 4。相比随机采样、系统采样和阈值分割采样，基于SSA采样方案生成的插值点与实测点皮尔逊相关系数平均提高了0.23、0.14和0.07。

本研究空间模拟退火算法的仅仅是针对单一目标优化，而在实际采样过程中影响采样工作的要素有很多，比如不同作物类型的种植结构导致的样点通达性都是影响采样效率的重要因素。在今后的研究工作中将引入这些要素，实现多目标优化，建立更为精细和实用的采样策略。

[1]姚云军，秦其明，张自力，等. 高光谱技术在农业遥感中的应用研究进展[J]. 农业工程学报，2008，24(7)：301-306.

Yao Yunjun, Qin Qiming, Zhang Zili, et al. Research progress of hyperspectral technology applied in agricultural remote sensing[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(7): 301-306. (in Chinese with English abstract)

[2]杨婷. 基于时间序列NDVI数据的中国熟制分布的变化研究[D]. 长春：东北师范大学，2014.

Yang Ting. Study on the change of maturity distribution in china based on time series NDVI data[D]. Changchun: Northeast Normal University, 2014. (in Chinese with English abstract)

[3]吴杨洁. 基于SPOT和NOAA数据的河北省干旱遥感监测研究[D]. 石家庄：河北师范大学，2012.

Wu Yangjie. Remote sensing monitoring of drought in Hebei Province based on SPOT and NOAA data[D]. Shijiazhuang: Hebei Normal University, 2012. (in Chinese with English abstract)

[4]张超. 1960—2015年内蒙古气候诊断及其与农田覆盖变化相互关系[J]. 中国农学通报，2016，32(32)：124-130.

Zhang Chao. Climate diagnosis and its relationship with farmland cover change in Inner Mongolia from 1960 to 2015[J]. China Agronomic Bulletin, 2016, 32(32): 124-130. (in Chinese with English abstract)

[5]刘玲玲，刘良云，胡勇. 基于AVHRR和MODIS数据的全球植被物候比较分析[J]. 遥感技术与应用，2012，27(5)：754-762.

Liu Lingling, Liu Liangyun, Hu Yong. Comparative analysis of global vegetation phenology based on AVHRR and MODIS data[J]. Remote Sensing Technology and Application, 2012, 27(5): 754-762. (in Chinese with English abstract)

[6]邢素丽，张广录. 我国农业遥感的应用现状与展望[J]. 农业工程学报，2003，19(6)：174-178.

Xing Suli, Zhang Guanglu. Application status and prospect of agricultural remote sensing in China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2003, 19(6): 174-178. (in Chinese with English abstract)

[7]晋锐，冉有华，柳钦火，等. 陆地定量遥感产品的真实性检验关键技术与试验验证[J]. 地球科学进展，2017，32(6)：630-642.

Jin Rui, Ran Youhua, Liu Qinhuo, et al. Key methods and experiment verification for the validation of quantitative remote sensing products[J]. Advances in Earth Science, 2017, 32(6): 630-642. (in Chinese with English abstract)

[8]李新. 陆地表层系统模拟和观测的不确定性及其控制[J]. 中国科学：地球科学版，2013，43(11)：1735-1742

Li Xin. Characterization, controlling, and reduction of uncertainties in the modeling and observation of land-surface systems[J]. Science China: Earth Sciences Edition, 2013, 43(11): 1735-1742. (in Chinese with English abstract)

[9]张仁华，田静，李召良，等. 定量遥感产品真实性检验的基础与方法[J]. 中国科学：地球科学版，2010，40(2)：211-222.

Zhang Renhua, Tian Jing, Li Zhaoliang, et al. Principles and methods for the validation of quantitative remote sensing products[J]. Science China: Earth Sciences Edition, 2010, 40(2): 211-222. (in Chinese with English abstract)

[10]Crow W T, Berg A A, Cosh M H, et al. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products[J]. Reviews of Geophysics, 2012, 50(2): 372-392.

[11]丁艳玲. 植被覆盖度遥感估算及其真实性检验研究[D]. 长春：中国科学院东北地理与农业生态研究所，2015.

Ding Yanling. Remote Sensing Estimation of Vegetation Coverage and Its Authenticity Test[D]. Changchun: Northeast Institute of Geography and Agricultural, Chinese Academy of Sciences, 2015. (in Chinese with English abstract)

[12]Atkinson P M. Optimal ground-based sampling for remote sensing investigation: Estimating the regional mean[J]. International Journal of Remote Sensing, 1991, 12(3): 559-567.

[13]Griffith D A, Haining R, Arbia G. Heterogeneity of attribute sampling error in spatial datasets[J]. Geographical Analysis, 1994, 26(4): 300-320.

[14]Stehman S S, Sohl T L, Loveland T R. Statistical sampling to characterize recent United States land cover change[J]. Remote Sensing of Environment, 2003, 86(4): 517-529.

[15]韩宗伟，黄魏，罗云，等. 基于路网的土壤采样布局优化—模拟退火神经网络算法[J]. 应用生态学报，2015，26(3)：891-900.

Han Zongwei, Huang Wei, Luo Yun, et al. Application of simulated annealing method and neural network on optimizing soil sampling schemes based on road distribution[J]. Chinese Journal of Applied Ecology, 2015, 26(3): 891-900. (in Chinese with English abstract)

[16]吴宗书，艾矫燕，李修华，等. 基于智能算法的矿区土壤修复采样优化[J]. 环境工程学报，2016，10(10)：5995-6000.

Wu Zongshu, Ai Jiaoyan, Li Xiuhua, et al. Sampling optimization in mine soil remediation based on intelligent algorithm[J]. Chinese Journal of Environmental Engineering, 2016, 10(10): 5995-6000. (in Chinese with English abstract)

[17]陈伟杰. 土壤特性的优化采样策略及空间离群样点检测算法研究[D]. 哈尔滨：东北农业大学，2019.

Chen Weijie. Research on the Sampling Strategies for Soil Properties and a Method for Spatial Local Outlier Detection[D]. Harbin: Northeast Agricultural University, 2019. (in Chinese with English abstract)

[18]Liang S L. Quantitative Remote Sensing of Land Surfaces[M]. New Jersey: John Wiley & Sons, 2003.

[19]赵英时. 遥感应用分析原理与方法[M]. 北京：科学出版社，2003.

[20]曾也鲁，李静，柳钦火，等. 基于NDVI先验知识的LAI地面采样方法[J]. 遥感学报，2013，17(1)：107-121.

Zeng Yelu, Li Jing, Liu Qinhuo, et al. A sampling strategy based on NDVI prior knowledge for LAI ground measurements[J]. Journal of Remote Sensing, 2013, 17(1): 107-121. (in Chinese with English abstract)

[21]Li H, Reynolds J F. On definition and quantification of heterogeneity[J]. Oikos, 1995, 73(2): 280-284.

[22]Matheron G. Principles of geostatistics[J]. Economic Geology, 1963, 58(8): 1246-1266.

[23]Krige D G, Magri E J. Geostatistical case studies of the advantages of lognormal-de Wijsian kriging with mean for a base metal mine and a gold mine[J]. Journal of the International Association for Mathematical Geology, 1982, 14(6): 547-555.

[24]Laslett G M, McBratney A B, Pahl P J. Comparison of several spatial prediction methods for soil pH[J]. European Journal of Soil Science, 1987, 38(2): 325-341.

[25]Metropolis N, Rosenbluth A W, Rosenbluth M N. Equation of state calculations by fast computing machines[J]. Journal of Chemical Physics, 1953, 56(21): 1087-1092.

[26]Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(6): 721-741.

[27]Guedes L P C, Uribe-Opazo M A, Ribeiro J P J. Optimization of sample design sizes and shapes for regionalized variables using simulated annealing[J]. Ciencia e Investigacion Agraria, 2014, 41(1): 33-47.

[28]Vandita S, Alfred S, David G R, et al. Simulated annealing with variogram-based optimization to quantify spatial patterns of trees extracted from high-resolution images[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(8): 1084-1088.

[29]雷秀强. 龙泉山脉中段植被叶绿素含量估算模型研究[D]. 成都：成都理工大学，2019.

Lei Xiuqiang. Study on Estimation Model of Vegetation Chlorophyll Content in Middle Longquan Mountains[D]. Chengdu: Chengdu University of Technology, 2019. (in Chinese with English abstract)

[30]范德芹，朱文泉，潘耀忠，等. 青藏高原小嵩草高寒草甸返青期遥感识别方法筛选[J]. 遥感学报，2014，18(5)：1117-1127.

Fan Deqin, Zhu Wenquan, Pan Yaozhong, et al. Screening of remote sensing identification methods for Kobresia alpine meadow in Qinghai Tibet Plateau[J]. Journal of Remote Sensing, 2014, 18(5): 1117-1127. (in Chinese with English abstract)

[31]李佳燕. 基于模拟退火算法的矿区复垦土壤监测样点布设研究[D]. 北京：中国地质大学，2019.

Li Jiayan. Optimal Sampling Design for Reclaimed Soil Monitoring in Mining Area Based on Simulated Annealing[D]. Beijing: China University of Geosciences, 2019. (in Chinese with English abstract)

[32]Ding Y L, Zhao K, Zheng X M, et al. Temporal dynamics of spatial heterogeneity over cropland quantified by time-series NDVI, near infrared and red reflectance of Landsat 8 OLI imagery[J]. International Journal of Applied Earth Observation, 2014, 30(1): 139-145.

[33]Wen Z F, Zhang C, Zhang S Q, et al. Effects of normalized difference vegetation index and related wavebands' characteristics detecting spatial heterogeneity using variogram-based analysis[J]. Chinese Geographic Sciences, 2012, 22(2): 188-195.

[34]Gallego F J. Stratified sampling of satellite images with a systematic grid of points[J]. ISPRS Journal of Photogrammetryand Remote Sensing, 2005, 59(6): 369-376.

[35]Filho C F F C, Albuquerque A T D, Costa M G F. Luminance optimization in closed environments by simulated annealing[J]. IEEE Latin America Transactions, 2008, 8(3): 229-235.

[36]Guedes L P C, Ribeiro P J, Piedade S. Optimization of spatial sample configurations using hybrid genetic algorithm and simulated annealing[J]. Chilean Journal of Statistics, 2011, 2(2): 39-50.

[37]Ruiz-Cárdenas R, Ferreira M A R, Schmidt A M. Stochastic search algorithms for optimal design of monitoring networks[J]. Environmetrics, 2010, 21(1): 102-112.

[38]Xiao X Y, Gertner G, Wang G X, et al. Optimal sampling scheme for estimation landscape mapping of vegetation cover[J]. Landscape Ecology, 2005, 20(4): 375-387.

[39]Groenigen J W V, Stein A. Constrained optimization of spatial sampling using continuous simulated annealing[J]. Journal of Environment Quality, 1998. 27(5): 1078-1086.

[40]Pausinger F, Rachh M, Steinerberger S. Optimal jittered sampling for two points in the unit square[J]. Statistics and Probability Letters, 2018, 132(1): 55-61.

[41]Rodeghiero M, Cescatti A. Spatial variability and optimal sampling strategy of soil respiration[J]. Forest Ecology and Management, 2008, 255(1): 106-112.

[42]Ge Y, Wang J H, Heuvelink G B M, et al. Sampling design optimization of a wireless sensor network for monitoring ecohydrological processes in the Babao River Basin, China[J]. International Journal of Geographical Information Science, 2015, 29(1): 92-110.

[43]Cochran W G. Sampling Techniques[M]. New Jersey: John Wiley & Sons, 1977.

Optimal sampling strategy for authenticity test in heterogeneous vegetated areas

Li Ruoxi1,2,3, Zhou Xiang1※, Lyu Tingting1, Tao Zui1, Wang Jin1, Xie Futai1,2,3

(1.,,100101,; 2.,100049,;3.,,,100049,)

With the rapid development of remote sensing technology, large-scale and high timeliness satellite products provide digital, quantitative, and mechanistic support for agricultural production. To evaluate the accuracy and uncertainty of vegetation products retrieved by remote sensing better, the sampling design is very important in the process of ground measurement experiment for validation in heterogeneous vegetated areas. In this study, the remote sensing image was regarded as the prior knowledge, the initial sampling points were selected by the K-means algorithm, and the optimal sampling scheme was planned by Spatial Simulated Annealing (SSA) algorithm. Then, the research scheme was verified by the field data of the same period. Based on the prior knowledge and geostatistics theory, it provided a strong theory for the sampling scheme. The essence of spatial simulated annealing algorithm is to search randomly, transfer state, accept (or discard) new solutions before the cooling cut-off, to find the optimal combination. By constantly jittering the new sampling combination, it jumped out of the local optimal solution, avoided the randomness of sampling, and could find more satisfaction. It meant that the initial positions of sampling points determined by stratified sampling were constantly combined and changed. Finally, the optimal combination that minimizes Kriging variance was obtained. Compared with other sampling schemes, it could be concluded that the SSA had stable advantages on different sampling numbers, the sampling accuracy was less affected by the number of samples, and the sampling combination with lower prediction error could also be found when the sample numbers were small. Under the condition of ensuring the sampling accuracy, the sampling quantity was obviously less than the traditional sampling scheme, which effectively reduced the sampling cost. The representativeness and accuracy of sampling points were evaluated by the relationship between sampling points and population, the scale of the trend surface and the real surface sample site. From the aspect of geostatistics, the sampling points obtained by SSA had better simulation ability to the sample population; From the aspect of Kriging interpolation, the Kriging variance of the sampling points optimized by SSA was 3-4 orders of magnitude higher than that of the traditional sampling points. The root mean square error between the interpolation surface and the image surface of the two sample areas based on the SSA algorithm was 3.102 6 and 2.962 7, respectively, and the Pearson correlation coefficient was 0.45 and 0.73, respectively. Compared with the other three sampling methods, the result of SSA was the smallest root mean square error and the highest Pearson correlation coefficient. Compared with random sampling, systematic sampling, and threshold segmentation sampling, the correlation between interpolation surface and image surface based on SSA improved by 29%, 30%, and 6%, respectively; the Pearson correlation coefficients of the interpolation points based on SSA and the measured points were 0.601 and 0.757, respectively, which were higher than those of the other three sampling methods. Compared with random sampling, systematic sampling, and threshold segmentation sampling, the correlation coefficients of interpolation points and measured points based on SSA increased by 0.23, 0.14, and 0.07 on average. It was proved that SSA could provide a reliable and optimized sampling strategy for the ground experiment of validation.

remote sensing; algorithm; sampling; authenticity test; heterogeneous vegetated areas

李若溪，周翔，吕婷婷，等. 植被异质性样区真实性检验的优化采样策略[J]. 农业工程学报，2021，37(8)：177-186.doi：10.11975/j.issn.1002-6819.2021.08.020 http://www.tcsae.org

Li Ruoxi, Zhou Xiang, Lyu Tingting, et al. Optimal sampling strategy for authenticity test in heterogeneous vegetated areas[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(8): 177-186. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.08.020 http://www.tcsae.org

2020-09-25

2020-11-18

国家重点研发计划项目（2018YFE0124200）

李若溪，研究方向为遥感陆表产品真实性检验。Email：liruoxi19@mails.ucas.ac.cn

周翔，研究员，研究方向为遥感真实性检验。Email：zhouxiang@radi.ac.cn

10.11975/j.issn.1002-6819.2021.08.020

TP79

A

1002-6819(2021)-08-0177-10