薄壁齿轮淬火变形有限元分析与改进

姜 辉，陈文革，陈茂进，杨一潇

(1.西安理工大学 材料科学与工程学院，陕西 西安 710048； 2.泰州进鑫机械有限公司，江苏 泰州 225300)

薄壁齿轮是一些相对自身尺寸壁厚较薄的环形齿轮和轮幅宽度较小的盘形齿轮，是目前工业装备制造中主要零件之一[1]，主要有传递动力、变速和改变运动方向等作用，故要求其表面有高强度、高耐磨性，芯部有高韧性，整体有良好的综合力学性能等[2]。为此通常要选用合金钢，并通过一定的热处理来满足这些性能要求，但热处理会造成翘曲变形、尺寸超差、硬度不均等问题。D.W.Kim等[3]对SCR420钢齿轮进行了渗碳处理发现齿轮有径向变形。J.R.Cho等[4]对锥齿轮进行了淬火处理发现齿轮出现了尺寸偏差。刘海滨等[5]对20CrMoTiH齿轮进行渗碳淬火处理发现齿轮出现轮齿胀大、椭圆变形及扭曲变形。邓影州[6]对20CrMo钢薄壁齿轮进行了渗碳淬火处理发现齿轮出现了椭圆变形和翘曲变形。张翠莹等[7]对20CrMnTi齿轮进行了渗碳淬火处理发现齿轮出现扭曲变形、硬度不均。李小末等[8]对薄壁齿轮进行了淬火处理发现齿轮出现了椭圆变形、平面翘曲。针对上述热处理造成的缺陷，很多学者进行了研究，如R.Husson等[9]在热处理前进行应力消除减小了齿轮箱轴齿热处理后的扭曲变形。张忠和等[10]在调整薄壁齿轮直径与壁厚比后降低了齿轮渗碳淬火后的椭圆变形。王培忠等[11]选择了合适的淬火油有效减小齿轮淬火时内花键孔的变形。张玉忠等[12]通过调整装炉方式改善了齿轮渗碳淬火后的扭曲变形、锥变。张凤林[13]通过改变齿轮渗碳淬火过程中的摆放方向降低了齿轮的锥变。李小末等[8]通过调整装炉方式改善了薄壁齿轮渗碳淬火后的平面翘曲变形。可见，以上的方法都只是通过多次的试验进行研究，费时费力费材。近年来，随着模拟技术的愈发成熟，越来越多的学者利用计算机模拟技术来研究齿轮的热处理变形问题，如王延忠等[14]利用Deform软件模拟了弧齿锥齿轮的渗碳淬火过程，提出了根据齿轮的使用要求选择合理的淬火温度。陈金明[15]通过使用ANSYS软件模拟了内齿轮的淬火过程，发现控制淬火冷却速度可以影响齿轮热处理变形。王鑫等[16]运用有限元分析手段分析了17CrNiMo6钢制齿轮轴的渗碳淬火过程，根据分析结果改善热处理工艺后减少了齿轮轴的热处理变形。高启林等[17]使用ANSYS软件模拟了锥齿轮的淬火过程，发现分级淬火可以使齿轮热变形更为平缓。刘赣华等[18]利用Deform模拟了弧齿锥齿轮压力淬火过程，通过调节压强参数控制了齿形变化。刘付洋等[19]利用Deform-HT有限元软件模拟了弧齿锥齿轮轮齿渗碳淬火过程，通过调整介质温度、保温温度等工艺参数减小了齿轮的变形。杨林等[20]利用有限元技术模拟了螺旋锥齿轮模压淬火的过程，发现不同淬透性齿轮最终热处理变形大小不同。姬朝阳等[21]利用有限元方法模拟了斜齿圆柱齿轮的单个轮齿淬火过程，提出了减少温差等控制齿轮热处理畸变的措施。由此可见，大多学者只是采用计算机模拟来研究具体的齿轮热处理方式、热处理工艺参数以及热处理造成的变形影响，对热处理过程中更易变形的薄壁齿轮的模拟则少见报道。为此本文采用有限元方法对45钢薄壁齿轮在不同装炉方式下淬火冷却过程进行计算机模拟，分析其温度场和应力场以及相应的变形规律，研究装炉方式对薄壁齿轮淬火变形的影响，并提出合理建议。

1 实际的薄壁齿轮及热处理工艺

图1是某厂提供的薄壁齿轮结构图和具体的技术参数。齿轮所用的原材料的化学成分如表1所示。采取的热处理工艺是 850 ℃淬火保温0.5 h，在不超过25 ℃水中冷却3 min，180 ℃回火保温1 h。计划采用两种装炉方式，吊装和平放，其装炉方式如图2所示。

图1 薄壁齿轮结构图及技术参数与要求Fig.1 The structure diagram and technical parameters requirements of thin-walled gear

表1 45钢化学成分(质量分数，%)Table 1 The chemical composition of 45 steel(mass fraction, %)

(a)吊装；(b)平放图2 齿轮装炉方式示意图(a) hoisting；(b) laying flatFig.2 Schematic diagram of gear loading method

2 建模及边界条件的设立

2.1 热传导微方程

物体内部温度随时间不断升高或降低，并经历相当时间后逐渐趋于周围介质的温度而最终达到平衡，这类传热过程为瞬态传热，齿轮淬火冷却过程中，只需考虑齿轮与淬火介质的传热过程，因此属于瞬态传热。基于傅里叶定律，根据热现象中的能量守恒定律，经过数学推广可以导出具有内热源瞬态条件下的三维热传导微分方程[22]：

(1)

式中：T为物体瞬时温度；t为淬火过程所需时间；λ为材料导热系数；ρ为材料密度；cp为材料的定压比热；Q为塑性功生成热和相变潜能；x、y、z为物体三维坐标位置。

2.2 初始条件和边界条件

齿轮淬火冷却过程是个瞬态问题，在分析齿轮淬火冷却时，需要定义初始条件，即要给出物体在初始时刻的温度分布情况[23]。

本文中假设初始时刻齿轮各处的温度都相同，所以初始条件为：

T=T0

(2)

式中：T0为初始温度，为均匀的850 ℃。

齿轮淬火过程中，淬火介质会与齿轮发生对流换热，根据能量守恒定律：

(3)

此即为齿轮对流换热边界[24]。式中：λ为材料导热系数；Γ为换热边界；α为表面换热系数；Tw为物体表面温度；Tf为介质温度，25 ℃，冷却时间3 min。

2.3 淬火应力应变场模型

ANSYS计算热应力有直接耦合与间接耦合两种方式，由于直接耦合的计算量过大，本文选取间接耦合的方式[25]。将热学分析的温度场结果作为应力分析的载荷导入至应力场模型，之后设置边界条件，因本文装炉方式有两种，所以需要设置两种约束，结合实际工况，平放约束下端面z方向的位移，吊装约束圆周面的z方向位移。在进行计算前，需要对齿轮材料热物性能参数进行设定。

齿轮在淬火过程中除了温度发生变化，组织也会发生转变，因此齿轮淬火过程中应力的计算要考虑应变、应变速率及温度的影响[26-27]，

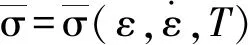
(4)

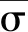
(5)

(6)

式中：mk为k组织质量体积分数；αk为k组织热膨胀系数：T为温度。

相变应变速率为：

(7)

弹性应变速率为：

(8)

式中：v为泊松比；E为弹性模量；σij为流动应力。

塑性应变速率为：

(9)

式中：H为加工硬化指数；σi为i方向上的应力。

相变塑性应变速率为：

(10)

式中：Kij为相变塑性系数；V为k组织的体积分数。

根据上述理论设定材料相关热物性能参数之后进行计算。

2.4 建立有限元模型

查阅文献可知[28-29]，45钢导热系数、比热容、水淬换热系数与温度的关系曲线如图3所示，45钢的密度为7850 kg/m3，弹性模量为6.5×105MPa，泊松比为0.29，热膨胀系数为1.6×10-5K-1。根据已知的齿轮参数进行三维建模，随后在workbench中进行网格划分，有限元网格采用四面体单元，因为四面体单元适合大多数比较复杂的模型。有限元模型共有83022个节点数和49929个单元数，如图4所示。

(a)导热系数；(b)比热容；(c)水淬换热系数图3 45钢性能与温度关系曲线(a) thermal conductivity；(b) specific heat capacity；(c) water quenching heat transfer coefficientFig.3 Relationship curve of properties and temperature of 45 steel

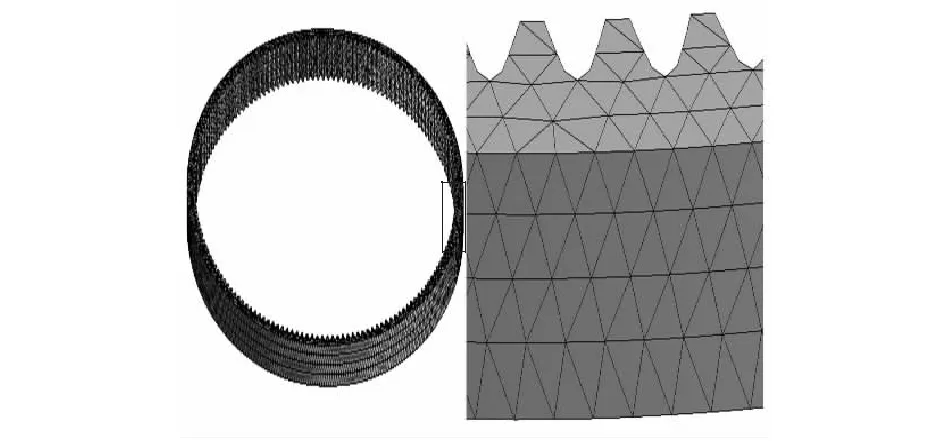
图4 有限元模型图，嵌入图为齿轮框选区域放大图Fig.4 Diagram of the finite element mode，the embedded diagram is an enlarged view of the gear selected area

3 模拟结果与分析

3.1 淬火冷却过程中温度场分布及分析

图5为齿轮在不同装炉方式下淬火冷却过程中不同时刻的温度场分布云图，图5(a)、5(c)、5(e)为齿轮吊装2、10和100 s的温度场分布图，图5(b)、5(d)、5(f)为齿轮平放2、10和86 s的温度场分布图。由图5(a)、5(b)可以看出，在2 s时齿顶的温度较低，齿根以及节圆内部的温度较高，此时平放、吊装齿顶的最低温度分别为134.54和102.91 ℃，节圆内部最高温度分别为712.26和699.41 ℃，温差分别为576.72 和596.5 ℃，温差较为明显。由图5(c)、5(d)可以看出，在10 s时平放、吊装齿顶的最低温度分别为46.352 和77.496 ℃，节圆内部最高温度分别为126.7 和167.1 ℃，温差分别为80.348和89.604 ℃，此时温差已显著减小。由图5(e)、5(f)可以看出，吊装、平放分别在100和86 s时，齿轮各部位均冷却至25 ℃左右，为了能够更加准确的研究齿轮不同位置的冷速特点，在齿轮上选取一些特征点绘制其温度随时间变化的曲线。

图6为薄壁齿轮上选取的特征点及其在不同装炉方式下的冷却曲线图，其中图6(a)为选取特征点位置的示意图；图6(b)、6(c)分别为齿轮吊装0～50和50～100 s各特征点冷却曲线图；图6(d)、6(e)分别为齿轮平放0～50和50～100 s各特征点冷却曲线图；图6(f)为齿轮平放时上下端面特征点0～10 s冷却曲线图。由图6(a)中可知，点a、b、c、d、e分别位于齿顶、齿根、节圆内部、齿轮上端面和齿轮下端面。由图6(b)～6(e)可以看出，齿顶处a点的冷速最快，齿根处b点、节圆内部c点冷速较慢。吊装时齿顶、齿根、节圆内部分别在100、104和104 s冷却至25 ℃，平放时齿顶、齿根、节圆内部分别在86、90和90 s冷却至25 ℃，由此表明在齿轮淬火冷却过程中，齿顶降温最快，齿根与节圆内部降温较慢。齿顶降温快是因为表面直接与淬火介质接触，发生剧烈的热量交换，而节圆内部并没有直接接触介质，因此冷速较慢，而对于齿根来说，因为其形状变化较大且较厚，所以冷却速度慢。正如文献[17]研究锥齿轮的淬火过程发现齿顶的冷却速度较快，且齿轮各部位冷速不同，导致齿轮在淬火冷却过程中不同部位出现了温差，有先增大后减小的现象。文献[30]也发现45钢圆柱齿轮淬火过程中不同部位存在温度差，且在开始阶段增大，随后不断减小。从图6(b)、6(d)中可以发现，齿轮各部位冷速前期较快，随着冷却的进行，冷速逐渐降低。文献[31]发现直齿轮表面淬火过程中前10 s内齿轮整体温度迅速下降，随淬火时间的延长，温度降低速率显著下降。从图6(f)可以看出，齿轮平放时上下端面在冷却初期出现温差，大概为30 ℃，随着冷却的进行，温差逐渐消失。综合分析图6可得，齿轮在不同装炉方式下的淬火温度场规律整体相同，区别主要在于齿轮平放时冷却初期上下端面存在温度差。

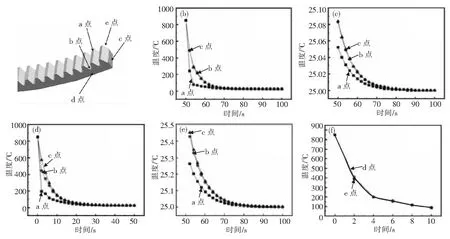
(a)选取的特征点；(b)吊装0～50 s；(c)吊装50～100 s；(d)平放0～50 s；(e)平放50～100 s；(f)平放不同端面0～10 s图6 薄壁齿轮上的特征点示意图及其在不同装炉方式下的冷却曲线(a)selected feature points； (b) hoisting 0～50 s；(c) hoisting 50～100 s； (d) flat laying 0～50 s； (e) flat laying 50～100 s； (f) flat laying different end faces 0～10 sFig.6 Schematic diagram of feature points on thin-walled gear and cooling curves under different furnace loading methods

(a)吊放2 s；(b)平放2 s；(c)吊放10 s；(d)平放10 s；(e)吊放100 s；(f)平放86 s图5 齿轮在不同装炉方式下不同时刻温度场分布图，嵌入图为齿轮框选区域放大图(a) hoisting 2 s；(b) flat laying 2 s；(c) hoisting 10 s；(d) flat laying 10 s；(e) hoisting 100 s；(f) flat laying 86 sFig.5 The temperature field distribution diagram of the gear at different moments under different furnace loading methods， the embedded diagram is an enlarged view of the gear selected area

3.2 淬火冷却后残余应力分布及分析

图7为齿轮在不同装炉方式下淬火100 s后的残余应力分布图。由图7(a)可看出，吊装时齿顶处的残余应力较小，齿根处残余应力较大；由图7(b)可看出，平放时残余应力最大点存在于齿根处。对比图7(a)、(b)发现齿轮吊放时残余应力整体较小。文献[32]分析了齿轮在不同装炉方式下淬火后的应力场，发现平放的整体应力比吊装的总体应力要高。

(a)吊装；(b)平放图7 齿轮在不同装炉方式下100 s淬火冷却后残余应力分布图， 嵌入图为齿轮框选区域放大图(a) hoisting；(b) flat layingFig.7 The residual stress distribution diagram of gears after 100 s quenching and cooling under different furnace loading methods, the embedded diagram is an enlarged diagram of the gear selection area

为了研究齿轮不同部位在淬火冷却过程中的应力变化，选取几个特征点绘制其应力随时间变化的曲线。图8为齿轮吊放、平放下0～100 s各特征点应力随时间变化曲线。可以看出，在淬火冷却过程初期，齿轮的应力急剧上升后急剧下降，之后随着冷却的进行又逐渐上升，最后趋于平缓。吊装时齿顶处的应力由0 MPa急剧上升至346.91 MPa后又急剧下降，最后逐渐升至150.6 MPa；齿根处的应力由0 MPa急剧上升至384.39 MPa后又急剧下降，最后逐渐升至227.31 MPa；节圆内部应力由0 MPa急剧上升至370.11 MPa后又急剧下降，最后逐渐升至178.77 MPa。平放时齿顶处的应力由0 MPa急剧上升至355.87 MPa后又急剧下降，最后逐渐升至150.6 MPa；齿根处的应力由0 MPa急剧上升至478.09 MPa后又急剧下降，最后逐渐升至255.56 MPa；节圆内部应力由0 MPa急剧上升至425.17 MPa后又急剧下降，最后逐渐升至191.73 MPa。

(a)吊装0～100 s；(b) 平放0～100 s图8 薄壁齿轮特征点在不同装炉方式下的应力随时间变化曲线(a) hoisting 0～100 s； (b) flat laying 0～100 sFig.8 The curve of stress variation with time of thin-walled gear feature points under different furnace loading methods

齿轮淬火冷却初期，齿轮表面由于直接接触介质，降温快，而心部要抵抗表面的收缩，心部出现压应力，表面出现拉应力，应力随表面与心部的温差增大而增大，达到最大值后又会随着心部与表面的温差减小而降低，减小到0后产生反方向的应力后继续增大。齿轮淬火过程中发生组织转变，主要是奥氏体向马氏体转变[33]，马氏体与奥氏体的组织特性如表2所示[34]。马氏体密度低于奥氏体，当发生马氏体转变时会出现体积膨胀，由于齿轮表面冷速快，所以会率先发生马氏体转变，这就造成表面相对于心部体积膨胀，心部要抵抗表面的膨胀，就出现了组织应力。随着冷却的进行心部达到了马氏体转变温度，开始发生膨胀，此时表面已经转变成高强度的马氏体，心部的膨胀又会受到表层的抵抗，随着心部体积的膨胀应力在某一瞬间暂时为0后，逐渐产生反方向的应力。因此在淬火冷却前期由于温度急剧下降与组织转变共同作用，便出现了应力急剧上升后又急剧下降的现象，后续随着冷却的进行，应力逐渐增大且最后趋于平缓[35]。这与文献[36]中工件淬火时应力变化规律一致。对比图8(a)、8(b)可以看出，淬火冷却后吊装的残余应力小于平放。由此可知两种装炉方式下，淬火冷却180 s后齿顶的残余应力都为最小，齿根残余应力比较大，不同部位之间存在应力差。齿根处应力大是因为齿根处受厚度、形状等因素影响，冷却不均匀，所以温度分布不均匀，导致产生较大的应力集中。文献[37]对圆柱齿轮的应力场进行了分析，发现应力最大值集中在齿根处。文献[17]发现锥齿轮淬火过程中齿芯、齿轮平面与齿顶应力出现了明显的差异。

表2 马氏体与奥氏体组织特性Table 2 Microstructure characteristics of martensite and austensite

3.3 淬火冷却过程中变形云图及分析

图9为齿轮不同装炉方式下淬火冷却100 s后的变形云图，吊装时齿顶、齿根、节圆内部最大变形量分别为0.054、0.058和0.056 mm；平放时齿顶、齿根、节圆内部最大变形量分别为0.066、0.069和0.068 mm。对比图9(a)、9(b)发现，吊装的整体变形量小于平放，齿顶、齿根处、节圆内部变形量分别小18.2%、15.9%和17.6%。由于平放时齿轮淬火瞬时接触淬火介质截面积大，且下端面较上端面先入水，导致瞬时两端面热应力不平衡，造成上端面凸起，齿轮翘曲过大；而吊装时淬火瞬时两个端面平行入水，入水截面小，热应力平衡对称，齿轮端面跳动

(a)吊装；(b)平放图9 齿轮在不同装炉方式下100 s淬火冷却后变形图， 嵌入图为齿轮框选区域放大图(a) hoisting ；(b) flat layingFig.9 Deformation diagram of gear after 100 s quenching and cooling under different furnace loading methods, the embedded diagram is an enlarged view of the gear selection area

小于水平放置。这与文献[8]薄壁齿轮的渗碳淬火变形基本一致。由图5、图8可知，薄壁齿轮在淬火冷却过程中，由于不同部位的冷速不同，使得工件内部出现了热应力；又因齿轮淬火冷却过程中发生奥氏体向马氏体转变的过程，体积发生膨胀，这就造成了组织应力的出现，热应力与组织应力共同组成了齿轮淬火时的内应力。不同部位应力大小不同，齿顶应力最小，齿根处应力最大。当内应力超过材料的塑形极限时，便发生了塑形变形，这是工件热处理变形的根本原因。

4 结论

45钢薄壁齿轮在850 ℃淬火时，齿顶降温最快，齿根及节圆内部降温较慢。平放时，齿顶在86 s下降到25 ℃，齿根在90 s下降到25 ℃，节圆内部在90 s下降到25 ℃；吊装时，齿顶在100 s下降到25 ℃，齿根在104 s下降到25 ℃，节圆内部在104 s下降到25 ℃。随淬火时间的延长，在不足50 s的时间内，齿顶与齿根的温差由最高的700 ℃迅速降低为不足1℃。两种装炉方式下，齿轮淬火冷却过程中均为齿顶温度最低，节圆内部温度最高，齿顶与节圆内部的温差随冷却的进行而减小。齿轮平放时先接触介质的端面率先降温，造成了不同端面之间存在温差，其温度梯度大概是30 ℃。

薄壁齿轮淬火过程中，平放时齿顶、齿根、节圆内部应力最大达到355.87、478.09和425.17 MPa，180 s后残余应力分别为150.6、255.56和191.73 MPa；吊装时齿顶、齿根和节圆内部应力最大达到346.91、384.39和370.11 MPa，180 s后残余应力分别为150.6、227.31和178.77 MPa。薄壁齿轮在不同的装炉方式下淬火后，吊装时的变形量小于平放，平放时齿顶、齿根、节圆内部变形量分别为0.066、0.069和0.068 mm；吊装时齿顶、齿根和节圆内部的变形量分别是0.054、0.058和0.056 mm。吊装相对于平放，齿顶、齿根和节圆内部的变形量分别减少18.2%、15.9%和17.6%。为减小薄壁齿轮淬火变形建议装炉方式采用吊装。