飞机前轮随滑行速度限偏的分析研究

唐瑞琳

（航空工业第一飞机设计研究院飞控系统设计研究所，西安710089）

0 引 言

飞机起飞降落进行滑跑时，虽然可以使用差动推力和差动刹车纠正飞机滑跑轨迹［1］，但这种方式会加大起飞降落滑跑距离，滑跑纠偏通常采用偏转前轮的方式。随着滑跑速度的逐渐增大，前轮偏转过大会引发飞机侧翻，从而导致飞机损毁。为了避免滑跑时侧翻现象的发生，通常会对前轮的偏转极限角度随速度变化进行限制［2］，速度越大对前轮偏转角度限制越大，前轮可偏转的角度也就越小。但并不是对前轮偏转极限角度限制越大越有利于飞机滑跑安全，对前轮偏转限制过大会降低飞机的滑跑纠偏能力，纠偏能力的降低有可能会致使飞机在起飞降落滑跑时冲出跑道［3］，因此合理地随速度变化限制前轮偏度可避免侧翻的同时最大保留飞机的滑跑纠偏能力。

国内外通常采用经验或者参考同类型飞机确定前轮随速度变化的限偏，理论研究相对较少。王孝英等［4］考虑了飞机在滑跑过程起落架受到的支反力和摩擦力，但是忽略气动效应；鲁胜等［5］考虑了滑跑过程中所受的气动力，但由于飞机侧翻体现为相对侧翻轴的外力矩，因此侧翻分析中需同时考虑到气动力和气动力矩；郭杰等［6］、刘刚等［7］、苑强波等［8］通过建立起落架动力学模型在不同速度下进行前轮不同偏转的数值仿真，得到临界侧翻时前轮偏转角，但是由于起降滑跑阶段飞机速度急剧变化，该方法不能反映出飞机加减速时的气动特性（特别是螺旋桨飞机起飞的大滑流特性和着陆时的刹车特性），因此采用起落架动力学模型仿真的方法也不能准确地得到飞机起降时前轮随速度的限偏；P.Sharpe［9］采用随速度指数衰减的形式限制前轮偏转范围，但指数衰减的限制形式及其参数没有具体的来源和方法。

本文通过研究飞机滑跑发生侧翻的原理，分析重力、气动、动力、刹车、前轮偏转对飞机侧翻的影响，计算起飞和降落状态下每个速度的侧翻临界前轮偏度和中立位，得到前轮随速度的限制范围。

1 侧翻分析

1.1 侧翻原理

滑跑时，当前轮偏转后，前轮轮轴地速方向很快改变并跟随前轮滚动方向。当达到稳态时，飞机转弯中心如图1所示，图中O为转弯中心，R为重心的转弯半径。由于转弯时，飞机是向心运动，飞机重心处受到离心力；起降滑跑阶段也是飞机加减速的阶段，飞机轴向上有惯性力，同时飞机重心还受到重力作用。滑跑时飞机有速度，气动参考点还受到气动力和力矩（即升力、阻力和侧力以及俯仰力矩、滚转力矩和偏航力矩）作用。起飞时发动机有最大的拉力，着陆时刹车相对重心受到低头力矩作用。

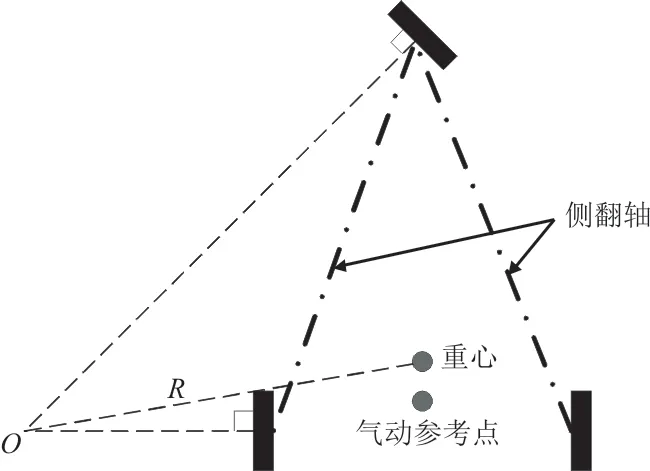
图1 转弯中心及转弯半径示意图［10］Fig.1 Diagram of turn center and turn radius［10］

所有这些力相对于前轮和主轮触地点连线（即图1中的点划线，以下简称为侧翻轴）的力矩与合力矩在侧翻轴方向的分量之和称为侧翻力矩，如果侧翻力矩不导致任一主机轮脱离地面，则不会发生侧翻，反之就会侧翻。

1.2 侧翻临界状态

根据侧翻原理的分析，飞机滑跑时发生侧翻主要是由于转弯产生的离心力相对侧翻轴的力矩过大，因此转弯半径越小、速度越大、重心高度越高越容易侧翻。计算不同速度下导致飞机即将侧翻（侧翻临界状态）的前轮偏度，可确定前轮随速度变化的限偏。

在滑跑过程中，随着飞机升力的增大，起落架的压缩量逐渐减小，重心高度是逐渐增大的。但机场跑道实际不是完全平整的，滑跑过程中飞机可能被颠起来，这种情况下重心的高度也会增加，因此按照各速度下所有起落架刚接地且没有压缩行程并即将发生侧翻认为是侧翻临界状态，取该状态的起落架尺寸进行计算。

2 侧翻轴的力矩

侧翻临界状态时，飞机相对侧翻轴合力矩为0，其中构成侧翻轴合力矩的分别有重力、气动力和力矩、动力、刹车、离心力。在不同速度下，可根据合力矩为0的关系求出侧翻临界状态的离心力，从而得到各速度下的前轮限偏。

定义机体构造坐标系，以飞机鼻锥为原点，x轴沿机身轴线向后为正，y轴垂直于飞机对称平面向右为正，z轴垂直于x-y平面向上为正，如图2所示。

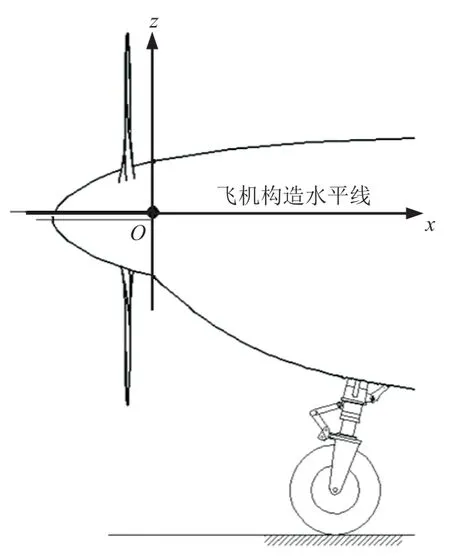
图2 机体构造坐标系示意图Fig.2 Diagram of engine construction system

2.1 重 力

重力对于侧翻轴而言，能提供一个抑制侧翻的力矩。重心相对于侧翻轴的力臂如图3中的实线所示，可根据起落架尺寸先求得前起落架轮轴到主起落架轮轴与前起落架轮轴到重心之间的夹角τ，再根据重心相对前起落架的位置求得重力相对于侧翻轴的力臂LG，如式（1）所示。

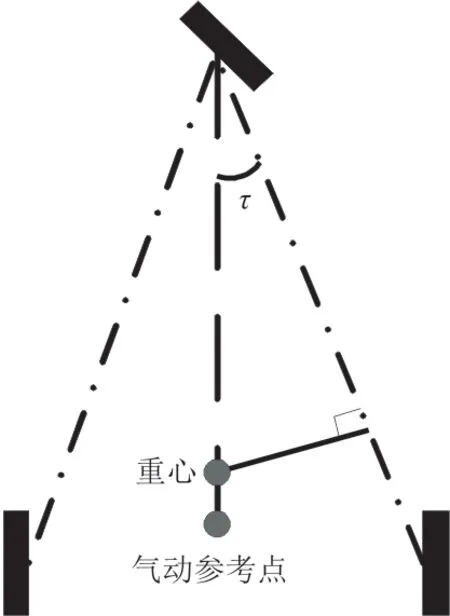
图3 重心相对侧翻轴力臂示意图Fig.3 Diagram of gravity center arm relative to cartwheeler axis

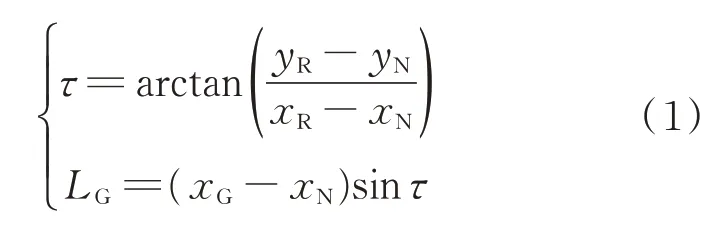
式中：（xR，yR，zR）为右主起轮轴在缓冲器没压缩时的机体构造坐标系坐标；（xN，yN，zN）为前起轮轴在缓冲器没压缩时的机体构造坐标系坐标。

因此重力相对于侧翻轴的力矩MG为

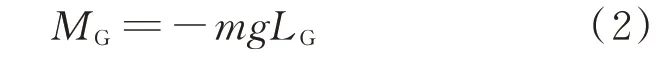
式中：m为起飞/降落质量；g为重力加速度。

2.2 气动力和力矩

气动力包括升力、阻力和侧力。其中升力提供促进侧翻的力矩；阻力提供抑制侧翻的力矩；侧力对于同侧侧翻轴提供一个抑制侧翻的力矩，而对异侧提供促进侧翻的力矩（理想转弯中，侧滑角都为0，但螺旋桨飞机由于滑流不对称，侧滑角为0时也有侧力）。

升力相对于侧翻轴的力臂L L如图4的实线所示，求取方法与重力力臂一致，如式（3）所示。

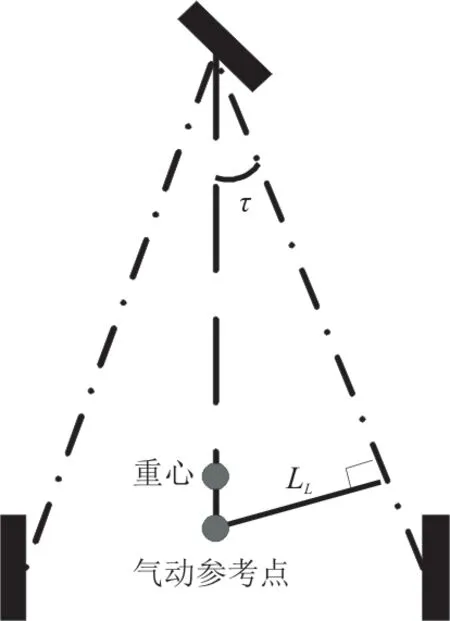
图4 升力相对侧翻轴力臂示意图Fig.4 Diagram of lift force arm relative to cartwheeler axis

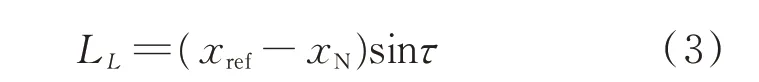
阻力和侧力相对侧翻轴的力臂L D、L Y是气动参考点距离地面的高度，即：

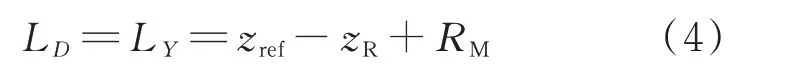
式中：RM为主起落架机轮半径。

气动力矩包括俯仰力矩、滚转力矩、偏航力矩。其中正俯仰力矩（抬头力矩）提供一个抑制侧翻的力矩，反之亦然；正滚转力矩对于右侧翻轴提供一个促进侧翻的力矩，对于左侧翻轴提供一个抑制侧翻的力矩，反之亦然；偏航力矩由于垂直于侧翻轴，所以对于侧翻不提供任何力矩，但其影响前轮的中立位。

俯仰力矩和滚转力矩可根据在相应侧翻轴方向的分量，将全机力矩转换到相对侧翻轴上。因此气动力和力矩相对于侧翻轴的总力矩Maero为

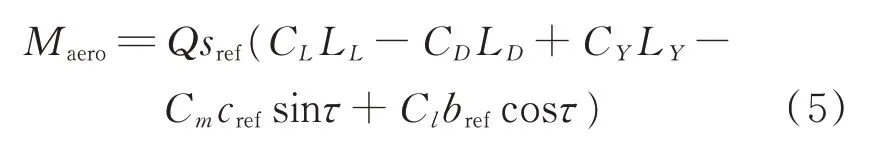
式中：Q为动压；sref为参考面积；cref为参考弦长；bref为展长；CL、CD分别为升力系数和阻力系数；CY、Cm、Cl为起飞/降落时的气动系数，即起飞时为满油门（大拉力系数）、降落时为小油门（小拉力系数）。

2.3 动 力

动力相对侧翻轴力矩示意图如图5所示。由于算例飞机的发动机位于机头，因此提供一个促进侧翻的力矩。

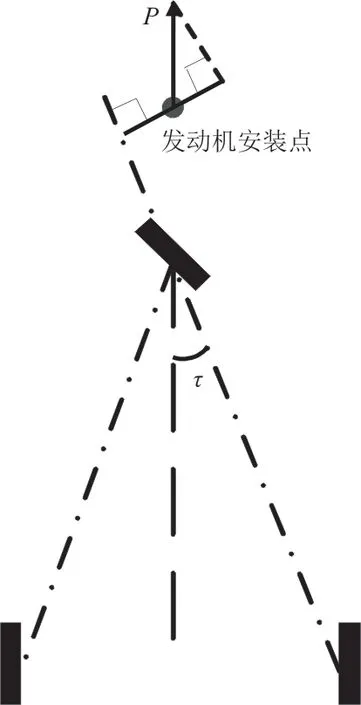
图5 动力相对侧翻轴力矩示意图Fig.5 Diagram of power arm relative to cartwheeler axis

由于发动机的力不垂直于侧翻轴，因此先根据起落架尺寸求取动力在垂直于侧翻轴方向的分力，而力臂为发动机安装点距离地面的高度，两者乘积为动力相对于侧翻轴的力矩M P。

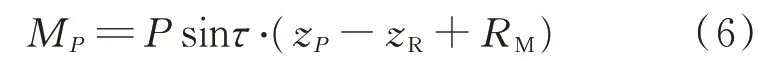
式中：P为发动机拉力；（x P，y P，z P）为发动机安装点在机体构造坐标系的坐标。

2.4 刹 车

只在降落滑跑过程中考虑刹车对侧翻轴的力矩。刹车时，机轮与地面的摩擦力增大，该摩擦力相对于重心产生低头力矩，因此提供了一个促进侧翻的力矩。轮胎正压力为重力与升力的差，刹车形成的机轮与地面的摩擦力是正压力与刹车摩擦系数的乘积，刹车力臂为重心距离地面的高度。将刹车力矩投影到侧翻轴方向，即可得到刹车相对侧翻轴的力矩MB。

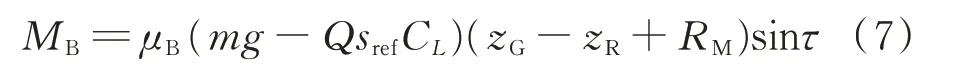
式中：μB为刹车时的轮胎摩擦系数。

2.5 离心力

重心处的离心力相对转弯外侧的侧翻轴提供了促进侧翻的力矩。离心力相对侧翻轴的力矩解算示意图如图6所示，重心处离心力方向与重心到转弯中心（如图6中的R所示）的方向一致，求取其相对侧翻轴的力矩Mc可先将其分解成垂直于飞机轴向和飞机轴线两个方向的力矩，然后进行叠加。

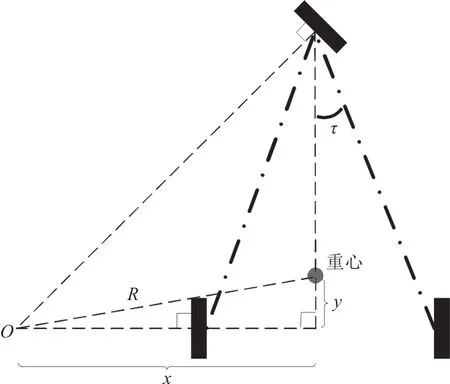
图6 离心力相对侧翻轴的力矩解算示意图Fig.6 Diagram of centrifugal force arm relative to cartwheeler axis

离心力相对侧翻轴的力矩Mc满足以下关系式：

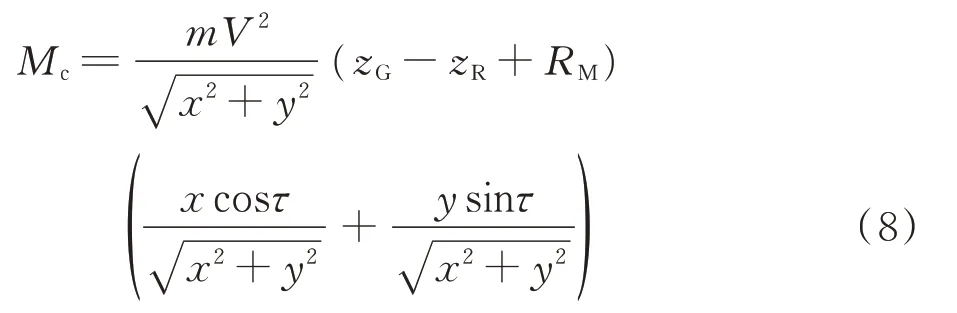
式中：

2.6 临界转弯半径及临界转向偏度

由侧翻临界条件可以得到：

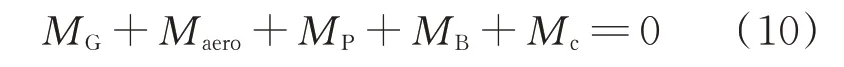
在各速度下，式（10）只有Mc中的x是未知量，为求得x，将式（10）改写为下列形式：

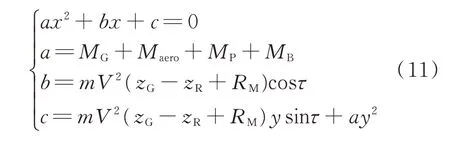
当升力小于重力，且x有正实根解时，可得临界转弯半径R。由一元二次方程通解可知，当

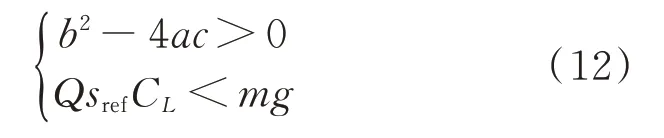
临界转弯半径：

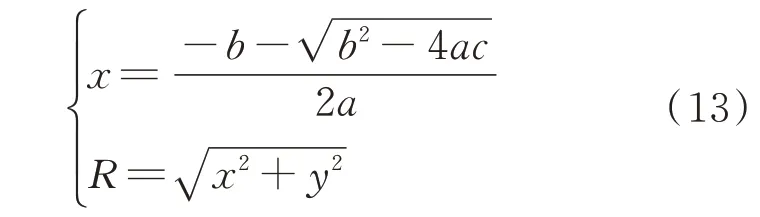
由此可得临界转向偏度δng：

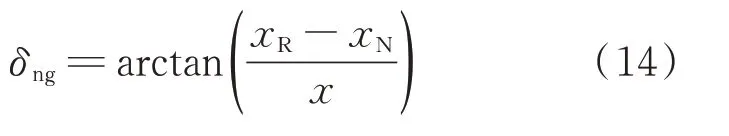
3 前轮偏度与滚动偏度的关系

如果前起落架转轴平行于机体构造坐标系的z轴，则滚动偏度和前轮偏度相等，而飞机前起落架一般有前倾角，因此前轮偏度和滚动偏度大致相同，但不完全一致。

机轮只受摩擦力作用时，保持在机轮轮廓平面内滚动，在机轮轮廓平面内垂直于轮轴到机轮触地点的向量在地面的投影就是机轮滚动方向，因此在求取前轮偏度与滚动偏度的关系前，需先求得前轮触地点。

建立机轮构造坐标系，以机轮轴心为原点，x轴在机轮对称面内平行于机体构造系x-y面向后为正，z轴在机轮对称面内垂直机体构造系x-y面向上为正，y轴垂直于轮胎对称面向右为正，机轮轮廓可由极坐标方程表示，如图7所示。

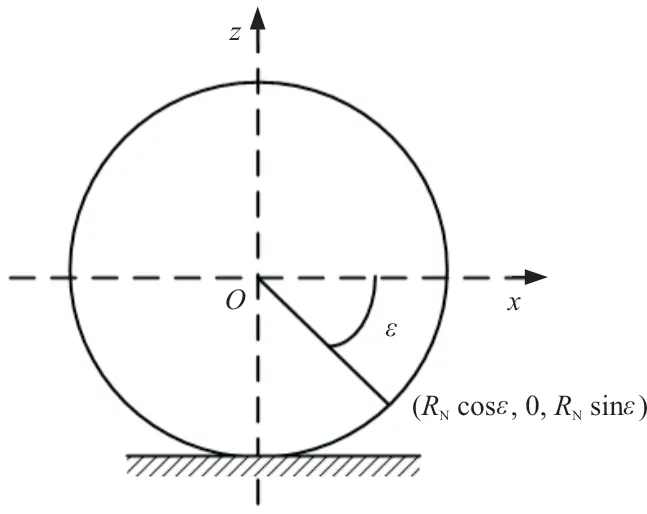
图7 机轮构造坐标系示意图Fig.7 Wheel structural coordinate system

将机轮构造坐标转换到相对于地面坐标，将机轮构造坐标系的z轴旋转与前起落架转向轴重合，经前轮偏转后再转换回机轮构造坐标系。因此机轮外轮廓坐标转换到地面的过渡矩阵为

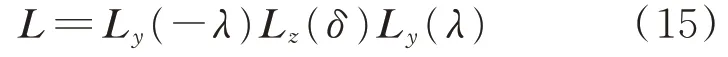
式中：δ为前轮偏度；λ为前起落架前倾角；L i(σ)为绕i轴旋转σ角的转换矩阵。

将机轮轮廓坐标转换相对地面坐标后，z坐标对极坐标因子ε进行求导，令其为0，可求得触地点的极坐标因子。

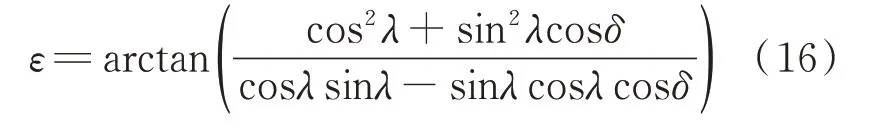
因此垂直于轮轴到机轮触地点的向量可定义为(-sinε，0，cosε)，滚动方向δng为

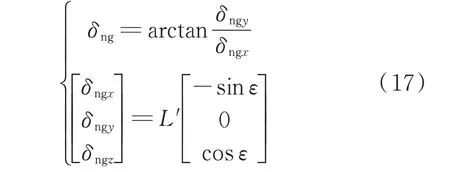
若起落架前倾角λ=12°，前轮偏度与滚动偏度的关系如图8～图9所示。

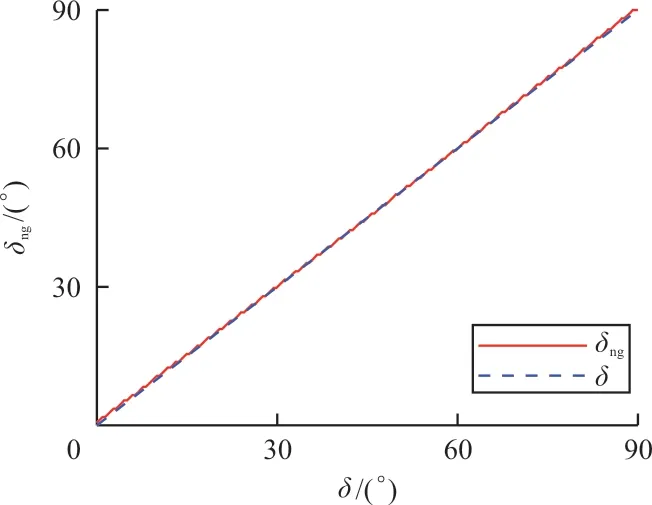
图8 前轮偏度与滚动方向的关系示意图Fig.8 Relaction diagram of nosewheel deflection with rolling direction

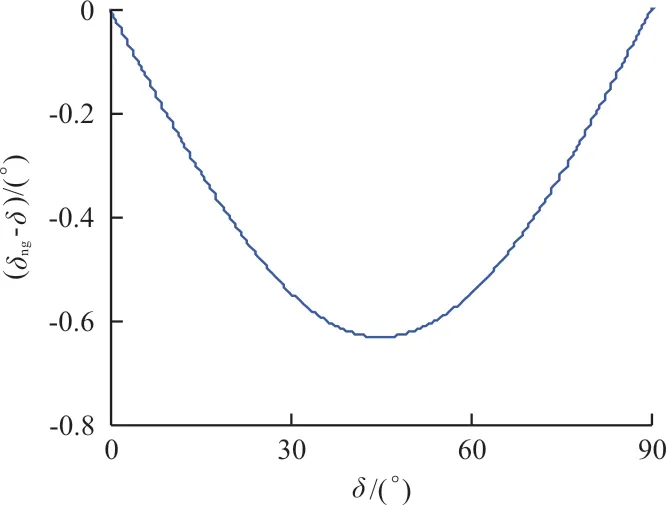
图9 前轮偏度与滚动方向的差Fig.9 The difference of nosewheel deflection with rolling direction

根据式（15）～式（17）可以求得δng，但通过式（14）得到的δng反推出δ的公式过于复杂。为了简化计算，根据式（15）～式（17）先计算出每个δ角度对应的δng，形成δ-δng插值表（如图8所示），再根据该插值表进行线性插值可由滚动方向偏度δng得到前轮转向偏度δ。

4 偏度随速度变化限制

根据前轮偏度与滚动偏度的关系，可求得前轮随速度变化的限偏，如图10所示。

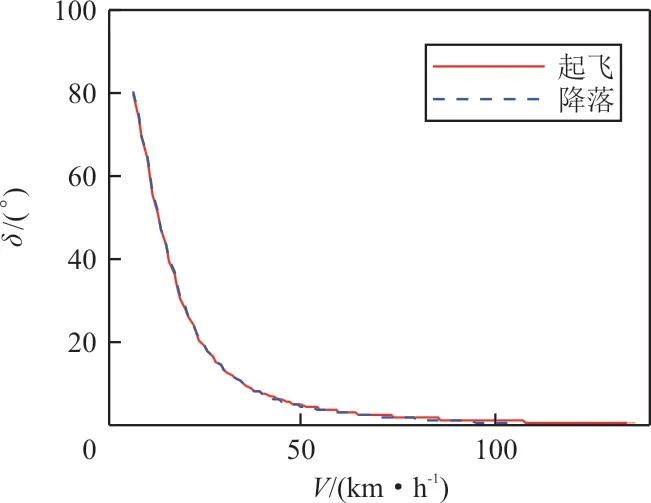
图10 前轮随速度的限偏Fig.10 Nosewheel deflection limit according to speed

从图10可以看出：前轮限偏角度与速度大致呈反比的关系，这与侧向过载一定时转弯半径与速度平方成反比相一致。

由于前轮机械极限偏度有限，低速时前轮偏度受机械极限的限制，因此考虑机械限制的前轮随速度变化的限偏如图11所示，其中起飞/降落构型的最大速度分别是抬前轮速度和着陆触地速度。

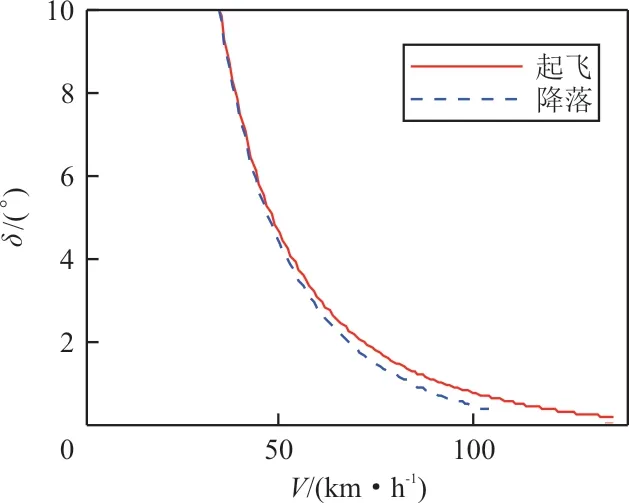
图11 机械极限限制下前轮随速度的限偏Fig.11 Nosewheel deflection limit according to speed base on mechanical limit

从图11可以看出：起飞/降落时在飞机离地前，前轮限偏都大于0，都保留一定程度的纠偏能力；同等速度下，由于降落构型的升力大，因此降落构型的限偏比起飞构型大；低速时，由于两种构型升力差距减小，限偏角度接近一致。

5 中立位的计算

由于飞机在滑跑过程中受不对称滑流或侧风的影响，气动偏航力矩和侧力不为0。这种情况下，上述限偏是相对中立位的增量值，而中立位不为0，前轮需要额外的偏度以平衡气动偏航力矩和侧力相对于重心的力矩。

令前轮支反力为FN，主起落架支反力为FM，根据力和力矩相等的关系，可求得各速度下的FN：

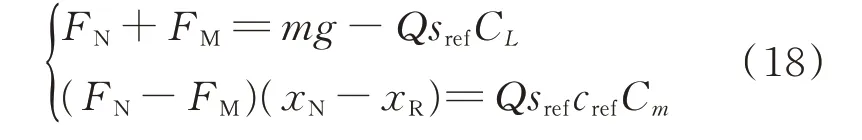
而前轮侧向力fN平衡气动偏航力矩，根据平衡关系：

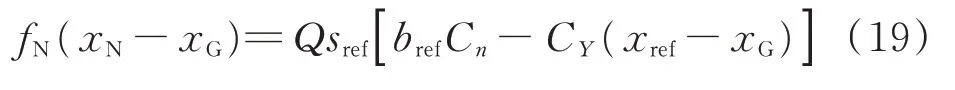
根据计算出的FN和fN，由轮胎试验曲线或者轮胎侧向力模型［11-12］可求得中立位，如图12所示。

图12 前轮中立位随速度变化的示意图Fig.12 Diagram of nosewheel neutral position according to speed

从图12可以看出：由于起飞时油门最大，不对称滑流更为严重，因此起飞构型下前轮的中立位比着陆构型更加偏置。

将中立位与限偏极性叠加即可得到前轮随速度变化的偏转范围，如图13所示。

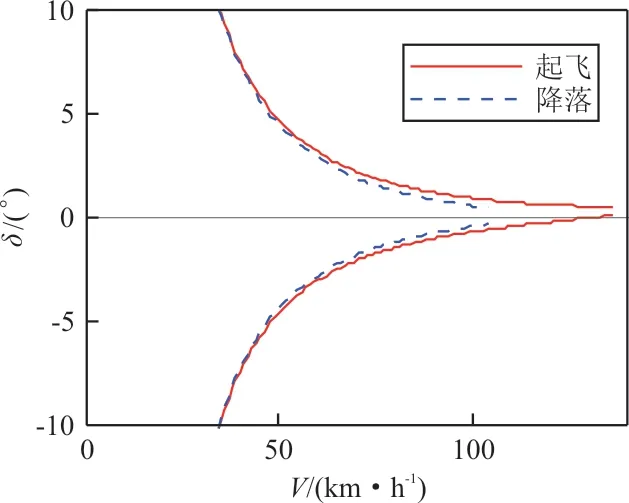
图13 前轮偏转范围随速度变化的示意图Fig.13 Diagram of nosewheel deflection range according to speed

6 结 论

（1）本文通过对飞机滑跑时相对侧翻轴力矩的分析计算，得到了前轮随速度的限偏及其中立位，计算结果符合前轮在不同速度下的偏转特性。

（2）由于升力相对于侧翻轴提供了利于侧翻的力矩，因此相同速度下，降落构型的前轮限制偏度更小。

（3）飞机在起降阶段的全滑跑速度范围内（起飞时小于抬前轮速度，着陆时小于触地速度）都具有不导致侧翻的前轮偏转范围，因此起降滑跑的全过程都可使用前轮进行纠偏。

（4）根据本文得到的前轮随速度的限偏范围，可以在防止侧翻的同时，保留飞机滑跑时最大的纠偏转弯能力。