倾转旋翼机连续倾转过渡状态数值模拟

2021-06-28吴伟伟马存旺张练孙凯军

航空工程进展 2021年3期

吴伟伟，马存旺，张练，孙凯军

（中国航天空气动力技术研究院彩虹无人机科技有限公司，北京100074）

0 引言

倾转旋翼机融合了直升机和固定翼飞机的特点，具有直升机垂直起降和固定翼飞机高效巡航的优势，在军事民用领域应用前景广阔。国外较早开展了倾转旋翼机的研究［1-3］，并成功研制了XV-15、V-22、BA-609，其中V-22大量装备部队。鉴于倾转旋翼机在军事领域优良的作战效能，美国在V-22基础上正在开展新一代倾转旋翼机V-280的研制［4］。近年来，倾转旋翼机在国内逐渐成为研究热点，多家科研院所及高校开展了关键技术研究和原理样机研制［5-9］。

倾转旋翼机在垂直飞行时，气动特性与横列式直升机类似，旋翼与机翼气动干扰严重［7，10-12］，在高速巡航时，气动特性与固定翼螺旋桨飞机类似［12-13］。倾转过渡是倾转旋翼机区别于直升机和固定翼飞机的主要特点，倾转过渡中倾转旋翼机的构型、重心不断变化，气动特性具有强非线性特点。倾转过渡状态的气动特性研究方法主要包括试验研究［12，14-15］和数值模拟［13，16］两种方法。试验方法获得的气动数据结果较为准确，但成本高、周期长。随着数值仿真技术的不断发展，数值计算结果与试验结果的误差逐渐减小，又由于成本低，因而获得了广泛应用。

国内外对倾转过渡的数值模拟研究主要采用稳定来流速度、固定总距角或固定倾转角度的方式进行计算［17-19］，而对倾转旋翼连续过渡状态的气动特性进行模拟的研究鲜有报道。基于此本文发展一套适合于模拟倾转旋翼机连续倾转过渡状态非定常流场的CFD方法，并对某型无人倾转旋翼机的连续倾转过渡状态进行模拟。

1 计算方法

1.1 运动嵌套网格

采用嵌套网格方法模拟旋翼和机体的运动。以某型无人倾转旋翼机［20］外形为例建立嵌套网格系统。受计算条件限制，为降低网格数量，采用半模结构，同时去除了尾翼、外翼、起落架及倾转短舱，计算模型网格由旋翼网格、机体网格及背景网格组成，如图1所示。模拟加速过程所需背景网格流场区域尺寸较大，为降低背景网格数量，采用1 m的网格尺寸。同时机体网格采用内密外疏，机体附近网格较密，与背景网格交界面处网格尺寸与背景网格尺寸一致。

图1 机体模型Fig.1 Plane model

桨叶网格为结构网格，附面层第一层厚度为5×10-5c（c为桨叶弦长），单个桨叶网格数量为446 232个；机体网格为非结构网格，网格数量为3 013 387个，旋翼旋转区域及尾流区域网格尺寸为0.2c；背景网格为结构网格，网格数量为158 400个，总网格数量为4 064 251个。采用主频2.2 GHz工作站20核并行计算，每个时间步旋翼旋转3°，迭代6次，单个时间步迭代计算时间约58 s。

为模拟机体和旋翼的加速平移运动，采用机体网格和旋翼网格整体同时作加速运动，旋翼网格在加速的同时作倾转、旋转、变距运动，可以真实地模拟倾转旋翼机连续倾转过渡状态的加速前飞运动。背景网格边界条件为自由来流，对称面处为对称平面。

1.2 控制方程

流场控制方程采用三维非定常RANS方程，其积分形式为

式（1）中符号意义及计算设置详见参考文献［21］。

1.3 旋翼和机体的运动

连续倾转过渡过程中，旋翼运动包括两部分，一部分是旋翼整体运动，如整体前飞加速、整体倾转；另一部分是旋翼自身运动，如旋翼旋转、变距、挥舞、摆振。机体运动包括前飞加速、俯仰、滚转、偏航以及舵面操纵。为降低运动模型的复杂度，在数值模型中旋翼模型忽略了挥舞和摆振，主要模拟旋翼整体前飞加速、倾转和旋翼桨叶旋转、变距运动，机体主要模拟前飞加速运动。连续倾转过渡参数线性变化时其运动方程为

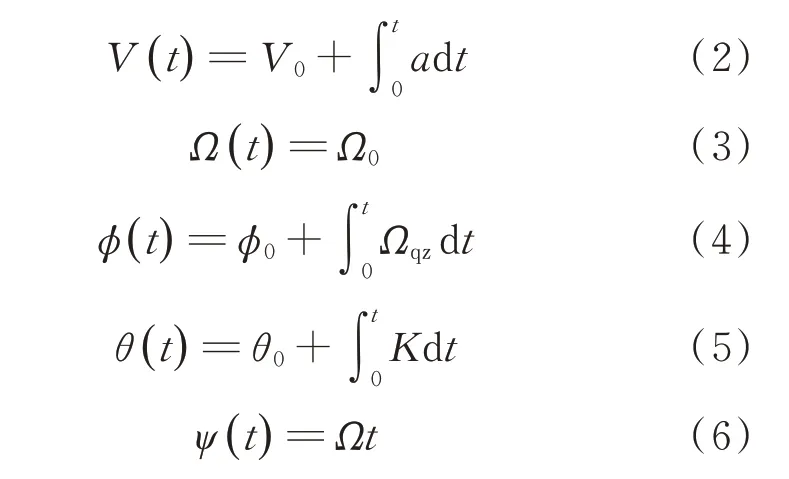
式中：V为机体和旋翼前飞速度；V0为机体和旋翼初始前飞速度；a为机体和旋翼前飞加速度；t为物理时间；Ω为旋翼旋转角速度，Ω0为倾转初始时的旋翼旋转角速度，在倾转过程中，旋翼旋转角速度保持不变；φ为旋翼倾转角（旋翼竖直状态为0°，水平状态为90°）；φ0为旋翼初始倾转角；Ωqz为旋翼倾转角速度；θ为总距角；θ0为桨叶安装角；K为总距角增加角速度；ψ为桨叶方位角。

倾转旋翼机在开始倾转过渡前，首先以直升机模式加速到初始速度，然后开始倾转过渡。

1.4 坐标系

倾转旋翼机在倾转过程中运动较为复杂，为便于描述机体和旋翼的运动采用局部坐标系，包括基本坐标系L（x，y，z），局部坐标系L1（x1，y1，z1），局部坐标系L2（x2，y2，z2）以及局部坐标系L3（x3，y3，z3），如图2所示。

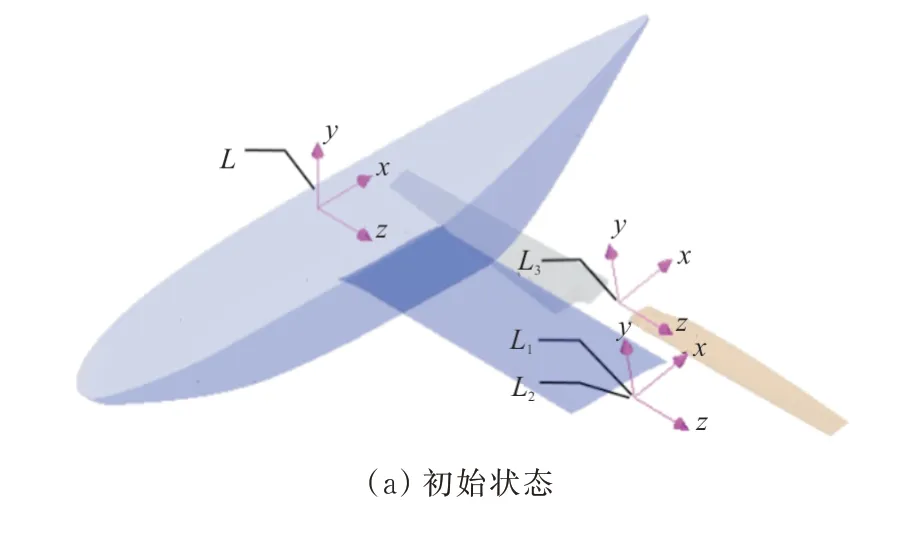
图2 坐标系Fig.2 Coordinate system

坐标系初始位置：基本坐标系L（x，y，z）原点位于机体对称面处，其z轴通过旋翼倾转轴线；局部坐标系L1（x1，y1，z1）由基本坐标系为L（x，y，z）沿z轴平移至旋翼轴，并绕z轴旋转至y轴与旋翼轴重合；局部坐标系L2（x2，y2，z2）与局部坐标系L1（x1，y1，z1）一致；局部坐标系L3（x3，y3，z3）由局部坐标系L2（x2，y2，z2）沿y轴平移至桨叶变距轴线。

坐标系运动：基本坐标系L（x，y，z）固定，机体和旋翼沿基本坐标系L（x，y，z）的x轴作加速平移运动，加速度为a；局部坐标系L1（x1，y1，z1）沿基本坐标系L（x，y，z）的x轴平移运动，运动速度与机体及旋翼运动速度相同，旋翼绕局部坐标系L1（x1，y1，z1）的z轴作倾转运动，倾转角速度为Ωqz；局部坐标系L2（x2，y2，z2）随坐标系L1（x1，y1，z1）运动并绕其z轴倾转，倾转角速度为Ωqz，旋翼绕局部坐标系L2（x2，y2，z2）的y轴作旋转运动，旋转角速度为Ω；局部坐标系L3（x3，y3，z3）随局部坐标系L2（x2，y2，z2）运动并绕其y轴旋转，旋转角速度为Ω，旋翼绕局部坐标系L3（x3，y3，z3）的z轴作变距运动，变距角速度为K。

2 算例验证

由于缺乏旋翼连续倾转过渡状态的相关试验数据，采用某型无人倾转旋翼机小角度倾转试验缩比桨［22］以及有试验数据可供对比的前飞状态的7A旋翼作为算例［23］验证本文方法。

1∶2.5缩比桨模型吹风试验在南京航空航天大学串置开口回流风洞进行，如图3所示。缩比桨可以俯仰偏转±10°。计算旋翼转速Ω=2 100 rpm，旋翼总距角θ=7.6°，风速V=9 m/s，缩比桨拉力系数计算值与试验值对比如图4所示，可以看出：拉力系数计算值与试验值基本一致。

图3 缩比桨风洞试验Fig.3 Wind tunnel test of scaled rotors

图4 Ct计算值与试验值对比Fig.4 Comparison between Ct calculation values and test values

7A旋翼半径R=2.1 m，桨叶弦长c=0.14 m［24］。计算状态：前进比λ=0.167，拉力实度比Ct/σ=0.08［23］。

旋翼拉力实度比Ct/σ每圈计算平均值和试验值对比如图5所示，可以看出：计算第5圈已收敛，Ct/σ=0.079 9，误差为-0.05%；计算第10圈，Ct/σ=0.080 2，误差为0.26%，误差较小。

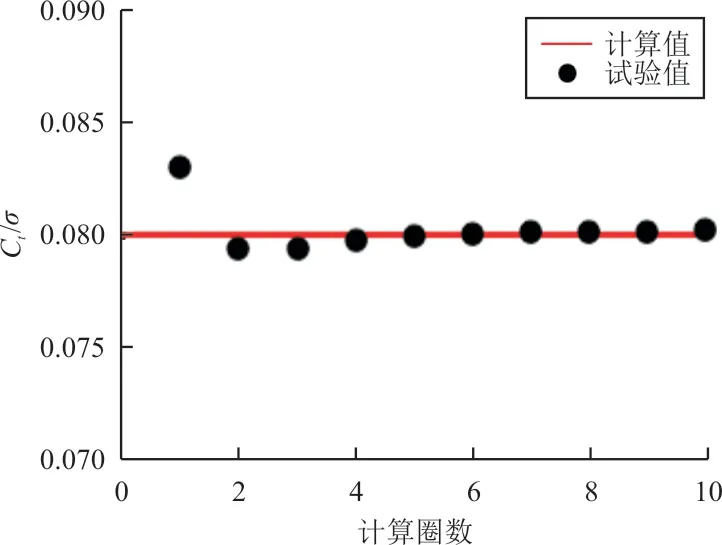
图5 Ct/σ计算值与试验值对比Fig.5 Comparison between C t/σcalculation values and test values

桨叶0.82R和0.92R截面处的压力系数在90°方位角和180°方位角计算值与试验值对比如图6～图7所示，可以看出：计算值与试验值吻合较好。

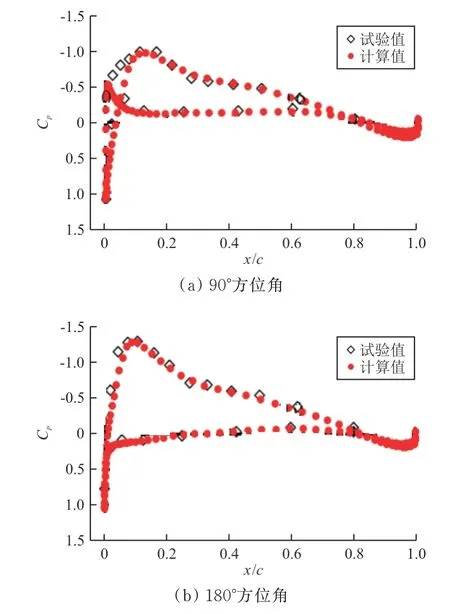
图6 0.82R处压力系数计算值与试验对比Fig.6 Comparison between pressure coefficient calculation values and test values at 0.82R

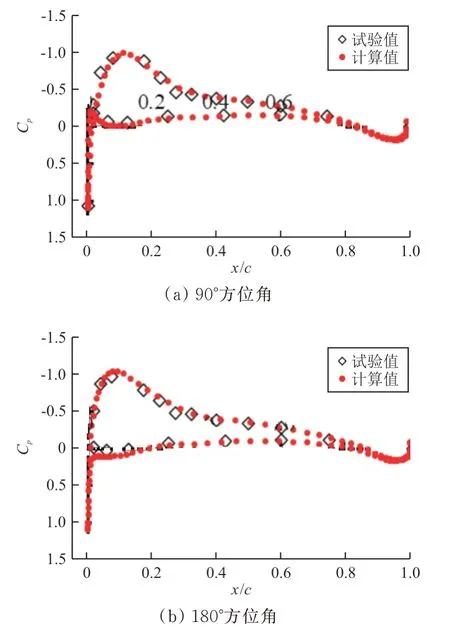
图7 0.92R处压力系数计算值与试验值对比Fig.7 Comparison between pressure coefficient calculation values and test values at 0.92R

上述算例验证说明本文方法所得计算结果与试验结果吻合良好，表明该方法合理，适合于倾转旋翼机气动特性的数值模拟。

3 连续倾转过渡过程模拟

3.1 不同过渡时间线性变化

由于连续倾转过渡迭代步数较多，连续倾转过渡时间越长，所需计算时间越长，对于计算资源要求越高。受计算条件限制，连续倾转过渡时间分别设定为1 s和2 s，连续倾转过渡参数线性变化，对比连续倾转过渡时间对气动特性的影响。

某型倾转旋翼机连续倾转过渡计算参数设置如表1所示，前飞速度、旋翼倾转角及总距角线性变化。在旋翼开始倾转前，先计算倾转初始状态流场，并达到收敛。初始状态流场如图8所示，并以此为初始条件，开始连续倾转过渡流场模拟。图中机体压力系数Cp机体=P/（1/2ρV2），桨叶压力系数Cp桨叶=P/（1/2ρΩ2R2）。

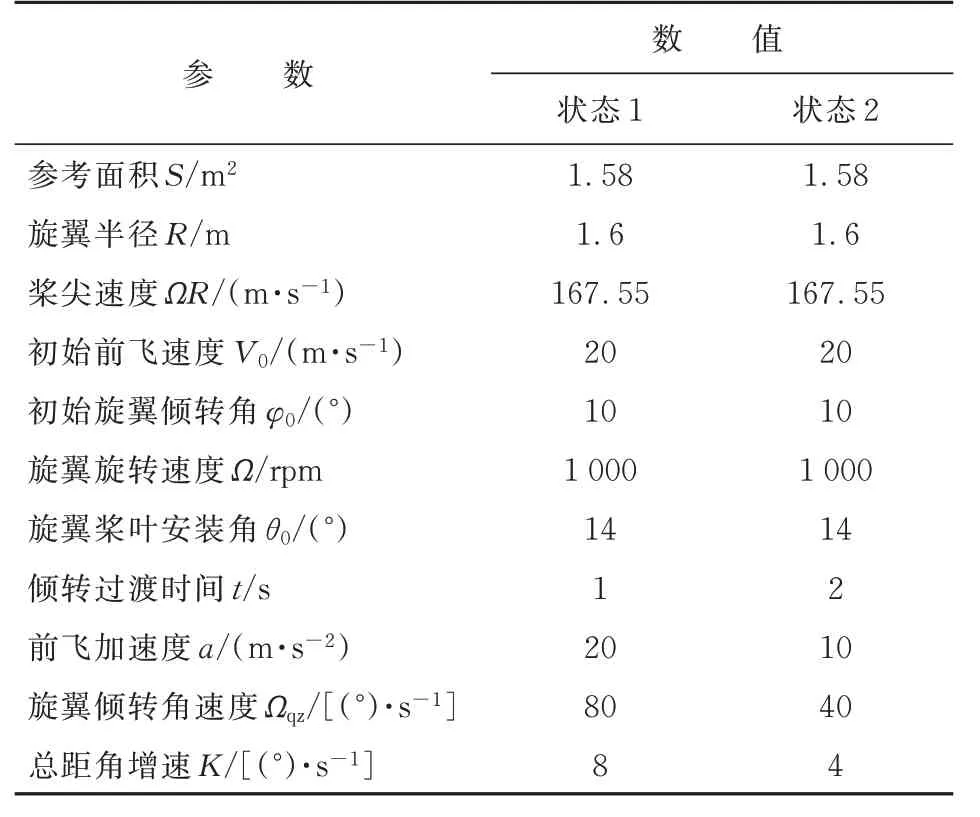
表1 连续倾转过渡参数Table 1 Parameters of continuous tilting transition

图8 开始倾转时压力分布和流场Fig.8 Pressure contour and flow field at the beginning of tilting

由于倾转旋翼机在连续倾转过渡中速度一直在增加，旋翼拉力系数Ct、扭矩系数CQ以及机体升力系数CL、阻力系数CD计算公式为

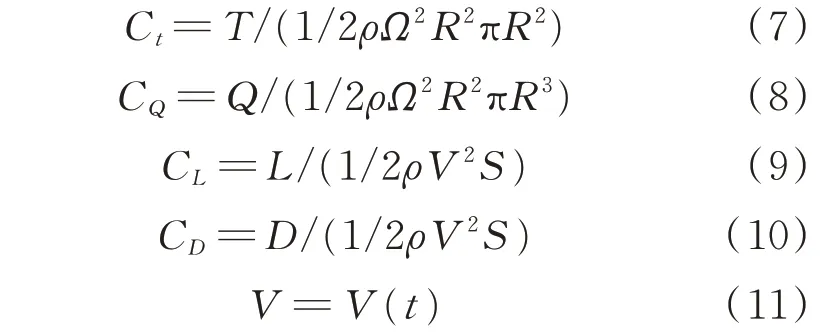
式中：T为旋翼拉力；Q为旋翼扭矩；L为机体升力；D为机体阻力；V为各时刻对应的倾转旋翼机飞行速度。

旋翼拉力系数随旋翼倾转角变化曲线如图9所示。

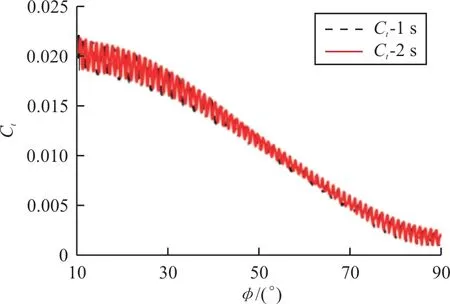
图9 旋翼拉力系数随旋翼倾转角变化曲线Fig.9 Curve of Ct varied withφ

从图9可以看出：连续倾转过渡时间为1 s和2 s时的旋翼拉力系数Ct随旋翼倾转角φ变化趋势一致，均随旋翼倾转角φ增加呈现逐渐减小的趋势，但连续倾转过渡时间2 s时的旋翼拉力系数Ct周期性变化频率是连续倾转过渡时间1 s时的旋翼拉力系数Ct周期性变化频率的2倍。这是由于随着来流速度增大及旋翼前倾角增加，虽然桨叶总距角同时增加，但其增加值小于桨叶迎角减小值，桨叶迎角减小。也可以看出：旋翼在倾转过程中，旋翼拉力系数Ct周期性变化幅值先减小后增大。这是由于旋翼在前倾过程中由于前行桨叶和后行桨叶气流不对称造成的旋翼拉力系数Ct周期性变化逐渐减小，而机翼对旋翼的气动干扰逐渐增加。

旋翼拉力系数垂向分量Ctc和前向分量Ctq随旋翼倾转角变化曲线如图10所示。

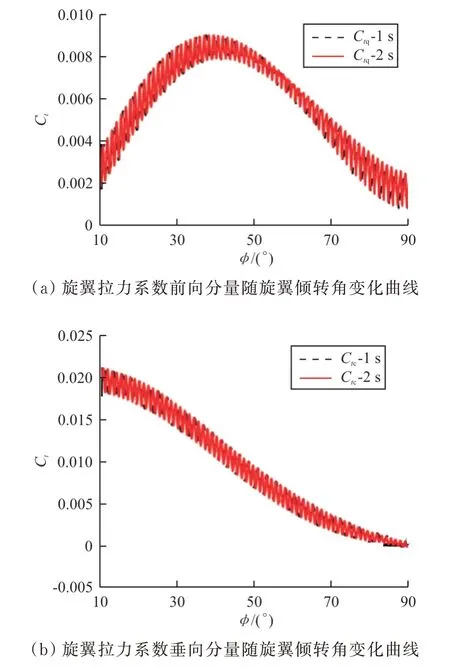
图10 旋翼拉力系数垂向分量和前向分量随旋翼倾转角变化曲线Fig.10 Curve of vertical component and forward component of Ct c and Ct q varied withφ

从图10可以看出：连续倾转过渡时间为1 s和2 s时的旋翼拉力系数垂向分量Ctc和前向分量Ctq旋翼倾转角φ变化趋势一致。随着旋翼倾转角增加，随旋翼拉力系数垂向分量Ctc逐渐减小至0，这是由于旋翼拉力系数Ct随旋翼倾转角增加逐渐减小，同时旋翼与垂向的夹角逐渐增大，而旋翼拉力系数垂向分量Ctc与旋翼拉力系数Ct近似成cosφ的关系，因此旋翼拉力系数垂向分量Ctc逐渐减小；旋翼拉力系数前向分量Ctq先增大后减小，在40°附近达到最大，这是由于旋翼与垂向的夹角逐渐增大，而旋翼拉力系数前向分量Ctq与旋翼拉力系数Ct近似成sinφ的关系，因此旋翼拉力系数前向分量Ctq先增大，随着旋翼拉力系数Ct进一步减小，旋翼拉力系数前向分量Ctq逐渐减小。

旋翼扭矩系数随旋翼倾转角变化曲线如图11所示，可以看出：连续倾转过渡时间为1 s和2 s时的旋翼扭矩系数随旋翼倾转角变化趋势一致，均随旋翼倾转角增加呈现先增大后减小的趋势，在40°附近达到最大。这主要是由于桨叶总距角线性增大，而旋翼入流增加较慢，因此桨叶迎角增加导致旋翼扭矩逐渐增大，但随着前倾角及前飞速度继续增大，旋翼入流增加加快，桨叶迎角减小，旋翼扭矩逐渐降低。

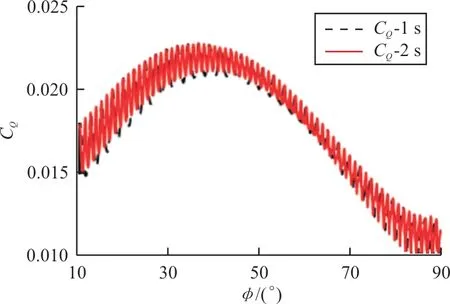
图11 旋翼扭矩系数随旋翼倾转角变化曲线Fig.11 Curve of CQ varied withφ

机体升力系数和阻力系数随旋翼倾转角变化曲线如图12所示，可以看出：连续倾转过渡时间为1 s和2 s时的机体升力系数CL和阻力系数CD随旋翼倾转角变化趋势一致。机体升力系数CL先增大后逐渐缓慢减小，在旋翼倾转角40°附近时达到最大，相比初始状态及平飞状态增大约30%。主要是由于随着旋翼前倾角度及前飞速度增大，旋翼下洗气流对机翼干扰逐渐减小，同时旋翼对气流有加速作用，旋翼加速气流随着旋翼前倾角增大对机翼的作用增强，但随着前飞速度增加，旋翼加速气流对机翼来流的影响逐渐降低，因此综合作用下来机体升力首先逐渐增大，在旋翼前倾角40°附近时达到最大，随后逐渐降低。机体阻力系数CD随着旋翼倾转角增加首先逐渐增大，在倾转至40°附近后变化较为缓慢，这是由于随着旋翼前倾角度及前飞速度增大，旋翼加速气流对机翼干扰逐渐增大，但随着前飞速度增加，旋翼加速气流对机翼的干扰逐渐降低。

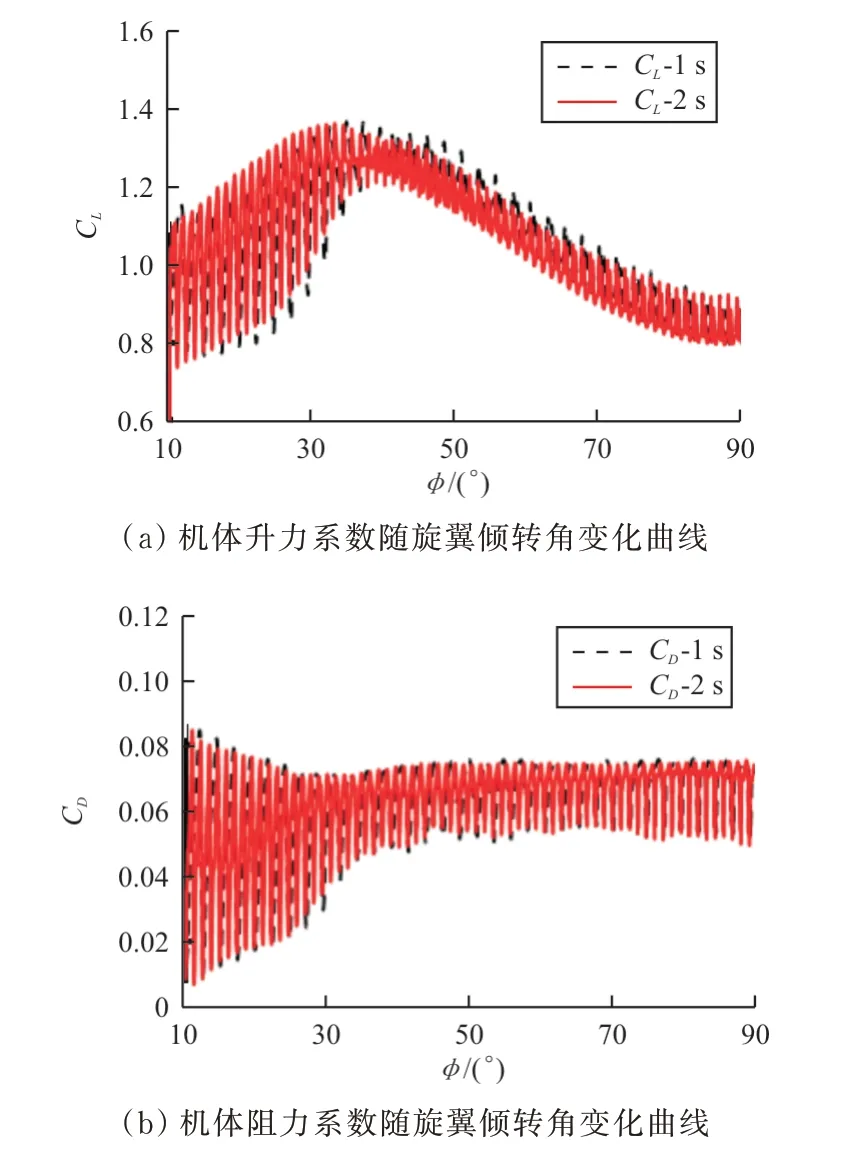
图12 机体升力系数和阻力系数随旋翼倾转角变化曲线Fig.12 Curve of CL and CD varied withφ

倾转过渡时间为2 s时，旋翼处于不同倾转角时机体和桨叶表面压力分布如图13所示，旋翼与机翼均处于平行状态。机体和桨叶表面压力相差较大，采用压力系数表示，机体表面压力系数Cp机体=P/（1/2ρV2），其中V为不同倾转角对应的前飞速度，桨叶表面压力系数Cp桨叶=P/（1/2ρΩ2R2）。

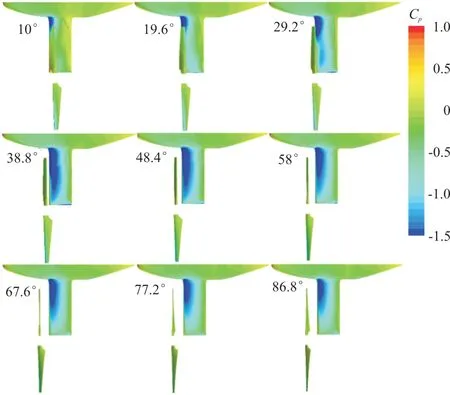
图13 不同旋翼倾转角机体和桨叶表面压力Fig.13 Pressure distribution on airframe and blade surface in different tilting angles

从图13可以看出：随着旋翼倾转角增大，机翼上表面负压区面积逐渐增大，在旋翼倾转角38.8°时达到最大，然后逐渐减小，说明旋翼对机翼的影响在38.8°附近时达到最大，这也解释了机体升力系数先增大后减小的变化趋势。

倾转过渡时间为2 s时旋翼处于不同倾转角时的全机流场如图14所示，旋翼与机翼均处于平行状态，可以看出：随着旋翼倾转角及前飞速度增加，旋翼桨尖涡向下倾斜角度逐渐降低，说明旋翼下洗流与来流速度的比值逐渐降低，旋翼下洗气流对机翼的干扰逐渐减弱。也可以看出：随着旋翼倾转角及前飞速度增加，两片桨叶的桨尖涡之间的距离逐渐增加。

图14 不同旋翼倾转角全机流场Fig.14 Flow field in different tilting angles

3.2 总距角非线性变化

倾转旋翼机在实际倾转过渡中总距角等参数不是线性变化，本文采用总距角非线性变化进行倾转过渡过程模拟，使得机体升力和旋翼拉力垂直分量之和（飞机总升力）变化尽量平缓，并与总距角线性变化进行对比。从倾转初始流场收敛后开始连续倾转过渡模拟，计算参数如表2所示，总距角非线性变化曲线如图15所示，其中状态2的总距角增速为非线性。

图15 总距角随时间变化曲线Fig.15 Curve ofθvaried with t

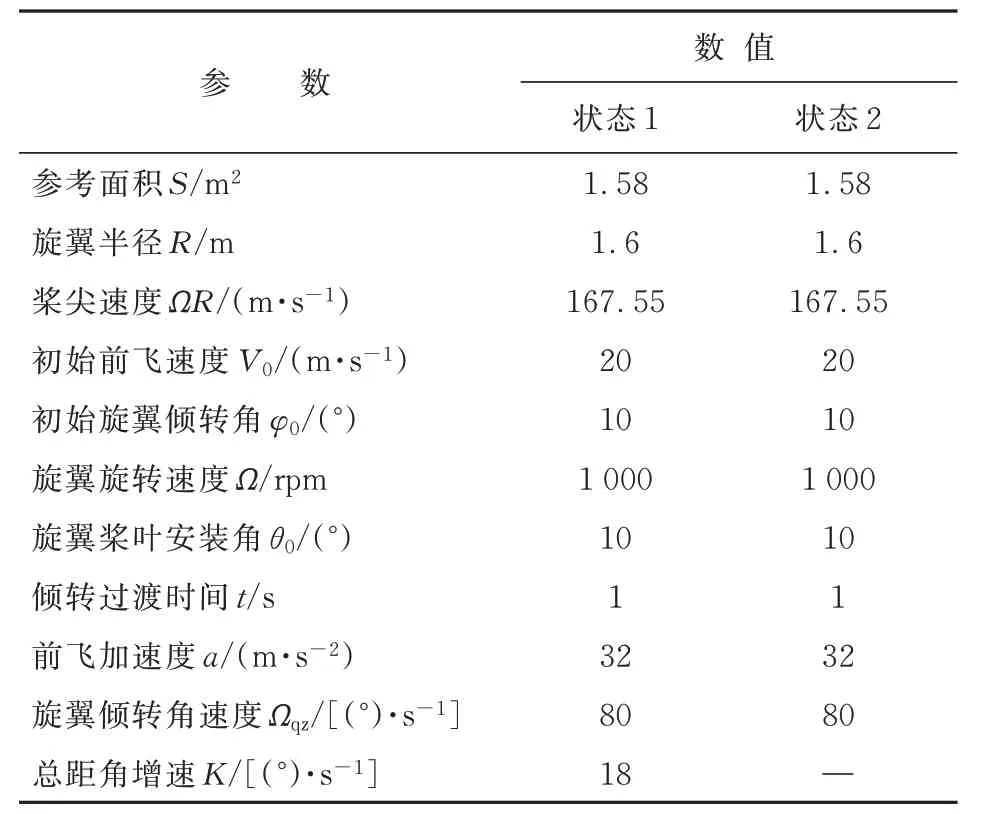
表2 连续倾转过渡线性及非线性变化参数Table 2 Linear and nonlinear parameters of continuous tilting transition

总距角非线性变化方程为

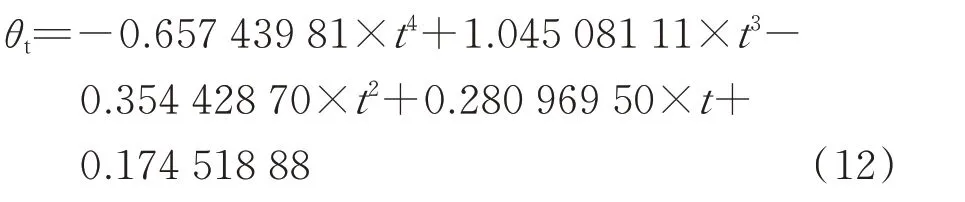
式（12）中，t从倾转开始时计时。

连续倾转过渡时总距角线性变化和线性变化气动特性对比如图16所示。

图16 总距角线性变化和非线性变化各气动参数对比Fig.16 Comparison of various aerodynamic parameters between linear and nonlinear changes in collective pitch angle

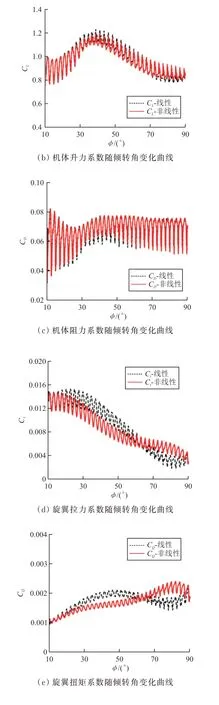
从图16（a）可以看出：总距角非线性变化时，倾转旋翼机的总升力随旋翼倾转角变化更为平缓，通过设计总距角非线性变化曲线，总升力可以保持在目标值附近；从图16（b）和图16（c）可以看出：总距角非线性变化和线性变化时的机体升力系数、阻力系数随旋翼倾转角变化趋势基本一致，机体升力系数均在旋翼倾转角40°附近达到最大值，相比初始状态及平飞状态增大约30%；从图16（d）～图16（g）可以看出：旋翼拉力系数及其前向分量和垂向分量、旋翼扭矩系数随旋翼总距角变化而变化，其变化趋势与总距角线性变化和非线性变化参数有关。