基于CFD耦合DEM并行算法的旋翼飞行器桨叶沙盲现象模拟分析

文韬，程党根

（1.长沙航空职业技术学院航空机电设备维修学院，长沙410124）

（2.空军航空维修技术学院 湖南省飞机维修工程技术研究中心，长沙410124）

0 引 言

旋翼飞行器在沙漠地区、雪地等具有离散相（Dispersed Phase）颗粒物的特殊环境中地效悬停IGE（In Ground Effect）或低速前飞时，会由旋翼下洗流带动并卷起大量沙尘或雪花，造成严重遮挡飞行员视线的现象被称为“沙盲（Brownout）”［1］。沙盲会极大地威胁飞行安全，还会对旋翼桨叶、发动机或机身本体造成严重的机械磨损［2-5］。

目前，研究旋翼飞行器沙盲现象采用的实验方法主要有粒子图像测速法（Particle Image Velocimetry，简称PIV）、半经验公式法、涡量输运模型法、黏性涡粒子法等。T.E.Lee等［6］基于PIV方法，在室内环境条件下，对缩比旋翼进行实验观察，发现了气动影响下近地附近沙尘扩散的过程、湍流的形成；B.T.Hance［7］对增加了机身的全机缩比模型进行沙盲实验分析，研究在沙盲环境下机身对旋翼桨尖涡所产生的影响；胡健平等［8］通过实验观察缩比旋翼模型在各种悬停高度时涡的状态，测量结果显示悬停高度在中间值时，桨尖涡的伸展现象明显超过耗散现象，但在增大悬停高度时，这种趋势则发生了逆转，同时采用雷诺平均方程和剪切应力输运湍流数值模型，通过碰撞接触模型的离散元模型，基于“多球法”构建了用于直升机地效飞行沙盲现象模拟的CFD-DEM耦合计算方法，对直升机在多种高度悬停下产生沙盲现象时沙尘颗粒的受力状态进行了分析，并对不同时间的沙尘运动形态和规律进行了计算，其研究结果表明，流场中大部分沙尘颗粒是不能形成沙尘云的，且外层空间的沙尘浓度比内层高，桨盘平面的上、下层区域的沙尘颗粒运动方向、切向速度各异，并与可得到的试验结果进行对比分析，验证了数值计算方法的有效性；朱明勇等［9］基于非结构网格技术和动量源模型的旋翼计算流体力学（CFD）方法，模拟贴地飞行时直升机旋翼非定常气动特性，且考虑了实际飞行环境下旋翼的运动操纵和旋翼配平特性，提出并建立了基于遗传算法和拟牛顿法的高效混合迭代算法，计算了特殊环境中地效悬停作用下的桨叶拉力增益、功率变化，有效解决了涡流理论方法较难模拟的“小速度前飞旋翼需用功率突增”问题。虽然上述方法能够较为精确地给出旋翼飞行器沙盲时沙尘的运动细节，但却很难采用全尺寸机身、桨叶进行实验，并且无法对多参数影响进行分析，相比之下，数值模拟则容易的多。然而，大多数数值计算方法都存在一些非常难以解决的问题，主要集中在以下三点：

（1）桨尖涡需要经过很长的时间才能传至地面，而在这个过程中涡极易耗散掉，而要减小耗散会极大地增加计算开销，尤其当旋翼距离地面较高时。

（2）要解决地面边界层以及边界处的湍流问题是极其困难的，尤其是采用非CFD方法。

（3）要很好地模拟流场和颗粒的相互作用也是具有极高难度的，颗粒的受力模型非常复杂，这也是目前的研究热点之一。

而且，当使用全尺寸的气动计算模型和颗粒形状各异、粒径分布广泛、受力复杂的沙尘颗粒进行耦合计算时，会造成巨大的计算资源消耗。

本文假设颗粒体积分数远小于流场计算域的10%，并且沙尘颗粒全部采用球体模型进行简化以控制计算开销。采用基于雷诺平均N-S方程及k-ω（SST）湍流模型，结合计算流体力学（Computational Fluid Dynamics，简称CFD）与离散元（Discrete Element Method，简称DEM）耦合并行算法，使用Fluent软件进行流场连续相计算沙尘的完整运动轨迹和颗粒分布。

1 流场计算方法

在沙尘颗粒所有的受力中，流场对其作用力是最为显著的，因而流场计算的准确性决定了沙尘颗粒运动的准确性。目前，研究两相流的观点主要有两种，一种观点认为流体是连续介质，颗粒群为离散体系；另一种观点认为流体是连续介质，颗粒群是拟连续介质或拟流体［10］。在有两种聚合物的混合体系中，离散相是被包围的聚合物，其对混合物机械性能的影响较小。连续相是对黏附、渗透、扩散、导热等性能参数影响较大的另一种聚合物。本文引入以变形后瞬时坐标为自变量的欧拉（Eulerian）坐标系，流场是建立在欧拉模型下的连续相。

1.1 物理模型

为了平衡计算精度和计算开销，采用的桨叶为缩比的单片NACA 0012翼型矩形桨叶，弦长0.1 m，根切16.67%，距离地面高度为0.3 m，半径为0.6 m，转速为200 rad/s，桨距为12°。

设置沙尘颗粒于桨盘正上方0.4 m处固定产生，以模拟桨盘吸入沙尘后随流场到达地面附近重新被流场卷起的过程。沙尘颗粒的物理特性及受力状态对于其在流场中的运动状态至关重要，作用于单个沙尘颗粒上的作用力非常复杂。从理论上分析，流场中运动的颗粒主要受到曳力、重力、Saffman升力、Magnus力、黏结力、附加质量力、Basset力、浮力等影响。通常，黏结力、浮力、Basset力和附加质量力由于相较其他力都非常小可忽略不计，而对于本文中颗粒体积分数远小于10%，从而可以忽略其对流场动量的影响，并且沙尘颗粒粒径微小，从而只考虑曳力和重力对颗粒移动速度和运动轨迹的影响。曳力采用不考虑孔隙率的Free steam模型［11］，计算公式如下：

式中：A为颗粒的投影面积；Cd为曳力系数。

式中：Re为雷诺数。

Saffman升力［12］是在有速度梯度的流场中颗粒两侧流场速度不一致而由低速侧指向高速侧的力：

式中：B为实验常数；ρ1为气相密度；η为气体黏性；Rd为颗粒半径；v1为气相速度；v2为离散相速度；∇为哈密顿算子。

Magnus力是由粒子自身旋转而产生的力，其表达式为

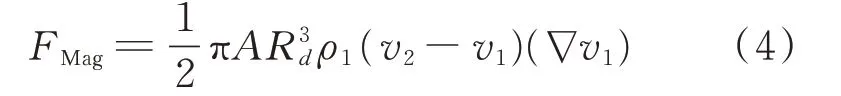
式中：A为经验常数。

对于沙尘或者粉尘这类颗粒极其微小的离散相，颗粒与颗粒之间的接触碰撞模型适合使用无滑移Hertz-Mindlin with JKR模型。为了节约计算资源而将其简化为球体模型，沙尘颗粒的物理参数设置如表1所示，其中，恢复系数用碰撞前法向相对速度与碰撞后法向相对速度的比值表示；滚转系数用滚动摩擦力矩与支持力的比值表示；静摩擦系数用最大静摩擦力与接触面间面积的比值表示［6］。

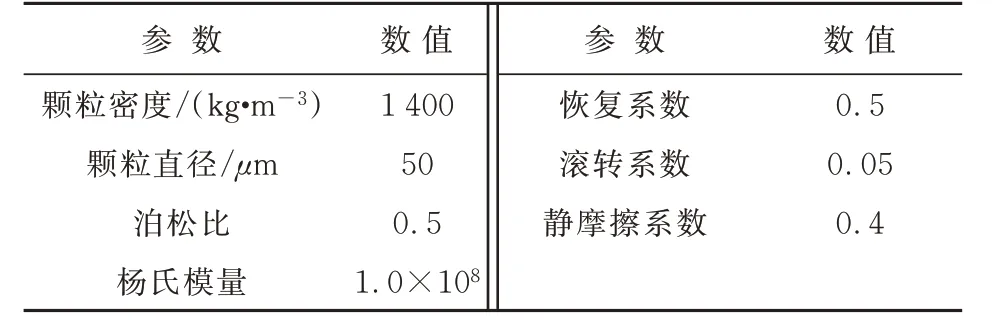
表1 沙尘颗粒的物理参数Table 1 Physical parameters of dust particles

沙尘颗粒初始状态的分布情况如图1所示，沙尘颗粒分布域为1.8 m2的正方形区域，平铺厚度为一层，颗粒数量为30 000颗，且为均匀分布、静止生成的球形颗粒。

图1 沙尘颗粒初始状态的分布情况Fig.1 Distribution of initial state of dust particles

采用ANSYS-Fluent软件计算连续相的悬停流场，采用EDEM软件计算离散相的灰尘颗粒，动量信息采用C++语言编译的API（Application Programming Interface）耦合接口进行数据传递，使用能从机理上反映连续相和离散相之间相互作用，并能真实反映出耦合特征的单向耦合模型Lagrange-Euler进行并行耦合计算。

1.2 网格系统

本文采用SMM（Sliding Mesh Method）技术，将计算域划分为桨叶附近的旋转区域和地效流场的静止区域进行瞬态求解，计算域之间通过Interface进行数据交换，旋转区域网格对于捕捉流场细节至关重要，弦长雷诺数为0.5×106，y+≈1，计算出第一层网格厚度约为4×10-6m。为了在保证计算精度，减小截断误差的同时控制计算开销，网格附面层增长率设置为1.2，并且采用桨叶表面网格以四边形为主和三角形混合的技术，在附面层使用各向异性的六面体网格具有比三棱柱网格更好的精度，而且还能在曲率较大的曲面很好地控制网格数量。在外层，六面体网格和四面体网格通过金字塔形网格进行连接。桨叶表面以及旋转区域网格如图2所示，计算域网格的剖面形态如图3所示。

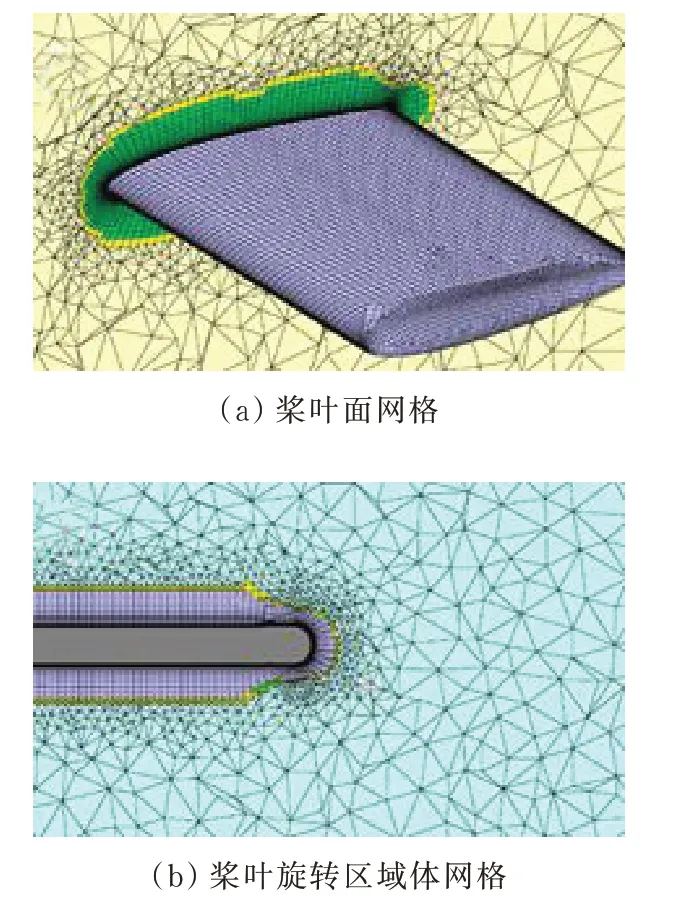
图2 桨叶网格模型Fig.2 Blade mesh and rotating area volume mesh

图3 计算域剖面网格［13］Fig.3 Calculation domain section grid［13］

静止区域的地面边界第一层厚度同样设置为4×10-6m，设置增长率为1.2，并且对桨盘直径长度附近的垂直地面方向的背景网格进行加密，以平衡计算精度和网格数量。

1.3 数值方法

DEM方法能够对处于流场中的每一粒沙尘颗粒的受力建立数学模型，准确地给出每一粒沙尘在每个时间步的运动状态以及受力情况，因而每一粒沙尘受到流场影响的空间扩散方式、运动轨迹等细节都能够详细呈现。

在CFD耦合DEM数值计算中，采用基于雷诺平均N-S方程的压力基求解器作为计算流体力学（CFD）软件的求解器［14］，使用Phase coupled SIMPLE算法求解，湍流模型选用能更好捕捉壁面速度梯度变化的k-ω（SST）两方程模型［15］，位于桨盘上部2R位置的顶部边界设置为压力进口，圆柱形远场侧面边界条件设置为压力出口，所有壁面条件设置为无滑移，对流相采用二阶迎风格式，扩散相采用中心差分格式，非稳态相采用二阶隐式格式求解［3］。

2 悬停流场与沙尘运动规律分析

2.1 悬停流场分析

旋翼飞行器利用地面效应悬停IGE状态具有和非利用地面效应悬停OGE（Out Ground Effect）完全不一样的流场，如图4所示。桨尖处的诱导速度在近地面处受到地面的阻碍，从而形成极大的滞止涡。康宁等［16］采用N-S方程对近地飞行的旋翼流场进行了数值模拟，分析了桨盘处诱导速度随各参数的变化规律，结果表明，在地面涡出现的飞行高度和速度范围内，桨盘前缘处下洗速度显著增加。在OGE状态下，桨根处流场直线向下，而在IGE状态下，流场受到地面阻挡形成高压区，流场方向与OGE状态相反，这与R.Sambaraju等［17］采用PIV的测试结果完全符合。

图4 计算域剖面速度场Fig.4 Velocity field of calculation domain section

2.2 沙尘颗粒运动轨迹的分布规律

流场稳定之后的近地面速度场是影响颗粒运动速度与轨迹的最重要因素，影响着颗粒在空间的分布状态以及运动轨迹。稳定后的流场速度分布如图5（a）所示，颗粒受流场影响刚到达地面的空间分布情况分别如图5（b）和图5（c）所示，此时的流场并未完全稳定，并且颗粒主要受到重力和诱导速度的影响于0.09 s到达地面附近，但是颗粒已初现受流场影响而呈现的螺旋型分布。

图5 近地流场速度分布以及沙尘颗粒刚接触地面后的分布Fig.5 Velocity distribution of near ground flow field and distribution of dust particles just after contacting the ground

随着流场进一步发展以及沙尘颗粒受到流场持续的影响，在空间呈现新的分布状况。0.17 s时沙尘空间分布状况如图6所示，可以看出：此时的沙尘已经开始受到桨根和桨尖处流场的影响，由于曳力比重力大而开始向空中卷起；桨根与桨尖之间由于并没有法向与地面的速度而部分开始向桨根中心移动，部分向桨尖处移动，这和流场计算的结果完全吻合。图6（c）定量地给出了中心—半径方向的颗粒数量分布，大量的颗粒分布集中于距离旋转中心1 400～1 900 mm的半径上，且桨根处也聚集了较高浓度的颗粒。

图6 0.17 s时沙尘颗粒分布Fig.6 Dust particle distribution at 0.17 s

当流场继续发展至0.3 s时，沙尘颗粒空间分布状况如图7所示，可以看出：桨根附近的沙尘颗粒已被流场卷起到了相当高度，如果在试验时飞行器有机身，则必然在机身贴壁面形成沙盲现象；同时，在大约2.5R之外处会有从地面卷起的扬尘，从颗粒数量统计可以看到，桨根处和桨尖处会将其间的沙尘向两端带动，在流场作用下沙尘颗粒被卷起形成沙盲现象。

3 结 论

（1）本文所提方法能够对旋翼飞行器利用地面效应悬停流场进行精确模拟，模拟结果与用PIV测试的结果完全符合。

（2）在对悬停流场进行模拟的同时，采用离散元计算方法能够对受流场持续影响的沙尘颗粒的空间分布状态及受力运动轨迹进行较好地模拟。

（3）相比较其他实验方法和半经验方法，本文方法能从形成机理上，多参数化地了解地效流场发展规律、细微沙尘颗粒受力运动和沙盲形成因果。

本文仍存在不足及需要改进的地方，例如流场远场计算域给定为4R，而颗粒运动计算域给定为正方形边长3R，从而导致很多粒子并没有形成扬尘就离开了计算域。而有些粒子会在壁面处沉积，这不符合物理现象，对于沙盲形成的整个过程的沙尘颗粒捕捉是不足的。其次，地效时的沙尘数量及其庞大，本文只给出一层沙尘设置在桨盘上方，这对于从地面卷起的现象模拟并不完全具有代表性，而对地面附面层的处理具有极高的难度。