三元锂电池模块热仿真风冷优化设计
2021-06-27王晓慧杨向前滕淑珍
王晓慧,吴 锋,杨向前,滕淑珍
(1.浙江工贸职业技术学院,浙江 温州 325000;2.浙江大学,浙江 杭州 310058;3.温州交运集团,浙江 温州 325000)
1 引言
锂离子电池具有比能量高,自放电率低,寿命长,无记忆效应等优点,已得到广泛应用。但是其所产生的热问题依然不可忽视。如果热量不能及时散失,便在有限空间累积,最终导致电池的温度升高,持续温升超过电池最大承受能力时,将产生热失控现象。故模块的散热设计显得尤为关键。这是因为锂离子电池的电化学性能、内阻和容量等均与温度密切相关,一旦模块内部的不同单体之间出现较大的温度差异,则必然体现出不同的性能并导致一致性的降低,进而影响电池组的循环寿命[1]。
因此,需要结合计算流体力学,针对不同的冷却介质选型,通过计算机仿真分析的手段进行模块热仿真的研究,准确地模拟不同环境与工况下模块的温度分布,从而为科学而高效[2-3]的模块热管理技术开发奠定基础。
2 模块热仿真模型
模块热仿真分析是建立在电池单体热仿真基础上的,然而电池单体的精细化建模必然意味着巨大的计算机开销,倘若简单地将精细化网格剖分的电池单体加以复制并放大至模块和系统层次,以现有的数值计算技术条件难以满足计算开销的需要。因此,必须对单体电池热仿真模型进行合理简化,这里是以简化后电池单体模型为基础而就建立的模块热仿真模型。
2.1 数学模型
建立笛卡尔坐标轴下的模块传热微分方程如下:

式中:x,y,z—空间三维各方向;λ—材料的导热系数;t—材料的温度;Φv—电池单体的产热功率;ρ—材料的密度;c—材料的比热容;τ—时间;Sh—对流传热量。
电池充放电过程的产热主要包括电芯和极耳这两大区域,前者包括电化学反应热和焦耳热,而后者仅为电流流经极耳和连接片产生的焦耳热。对电芯部分的产热,统一由Bemardi电池生热速率方程[5]给出:

式中:I—电流;V—电芯体积;Eoc—电池平衡电动势;U—电池工作电压;T—电池初始温度取298K;—电池电压随温度变化的温度系数,一般取0.22mV/K。Eoc和U的数值可由充放电曲线计算得到。
电池与外界主要通过对流散热,其传热速率遵守对流传热公式:

式中:A—暴露于环境中的电池外表面面积;h—对流传热系数,与
随着对农业面源污染研究的深入,可以发现,仅靠单一的控制措施无法彻底防控农业面源污染,因而对农业面源污染防控措施的研究开始从单一措施演变到多方法、多角度、多层次的综合措施,即通过建立污染控制措施体系进行控制。在这方面,美国最具代表性,其在20世纪70年代提出的“最佳管理措施”(Best Management practices, BMPs)是典型代表。BMPs使得农业面源污染控制摆脱了单一手段难以应对的困境,它已由一种确定的手段、方法演化成一种思想、理念。目前,BMPs是一个日趋完善的关于预防、应对、控制农业面源污染的措施集对于具体区域和问题的响应[6]。
环境空气流速、温度和壁面粗糙度等有关,可通过计算流体力学分析依据怒塞尔准数等进行计算;Δt—电池外壳与环境的温差,其取值随着放电过程中电池的温度的变化而改变。
冷却介质流动过程遵守质量、动量和能量三大守恒规律,可以写成通用控制方程:

其中,从左至右分别代表瞬态项、对流项、扩散项和源项,其中模块充放电过程中的产热功率以源项的形式均匀加载至单体内电芯的网格区域。
2.2 实体模型与有限元网格
以2P10S模块为研究对象,在Icepak软件平台建立实体模型并划分网格,如图1、图2所示。

图1 2P10S模块实体模型Fig.1 2P10S Module Entity Model

图2 2P10S模块计算网格中截面Fig.2 2P10S Module Calculation Grid Section
2.3 边界条件与初始条件
根据前文所述数学模型并结合实际情况,设置的边界条件如下:
(1)按照式(2)的计算结果以热量体积源项的方式在所有电池单体内部的电芯网格区域均匀施加产热功率,其大小与充放电倍率和时间有关。
(2)外界环境冷却空气从图2计算域除底面以外的五个面分别进出计算域,考察的环境温度为22℃,底面与环境之间始终存在换热,取换热系数为2W/m2·℃。自然冷却时,上述五个面均为自由边界条件;强制风冷时,计算域的左右两个小面和上表面为自由边界条件,前后两个大面则为冷却空气的速度入口,根据实测结果设置空气流速0.2m/s,温度15℃,空气流动方向与前后两个大面垂直。
(3)初始条件方面,设置整个模块的初始温度与环境温度保持一致,为22℃;计算域中空气有着竖直向上的大小为0.01m/s的初始流动,空气温度也与环境温度一致,为22℃。
3 不同冷却条件下的模块热仿真分析
3.1 自然冷却条件下的模块热仿真分析
自然冷却条件下,模块从满电态开始1C恒流放电至截止电压3.0V,放电结束时刻整个计算域(模块及其周围空气环境)的垂直中截面温度分布,如图3所示。

图3 自然冷却条件下计算域中截面的温度分布Fig.3 Temperature Distribution of the Cross Section in the Calculation Domain Under Natural Cooling Conditions
图3中,空气区域的温度基本保持在(22~26)℃(295~299)K之间,模块正上方空气温度比其他区域略高;而模块的温度则大大超过周围环境的空气温度。选取模块区域的电池单体及单体间隔离片,得到其温度分布,如图4所示。

图4 自然冷却条件下模块中截面的温度分布Fig.4 Temperature Distribution of the Cross Section in the Module Under Natural Cooling
图4中可以更为细致地观察到组成模块的各单体电池的温度分布,除了最外端2pcs单体的温度比中心单体高1.5℃左右,总体来看模块整体的温度差距控制得较好,温度最高的中心处和温度最低的角部温差控制在2℃以内。从左至右各单体中心点位置的温度比较,如图5所示。图中横坐标为位置,纵坐标为温度值。

图5 自然冷却条件下模块各单体中心点的温度分布Fig.5 The Temperature Distribution of the Center Points of Each cell of the Module Under Natural Cooling
模块附近的空气流动情况的流线图,如图6所示。图中可见冷空气被模块加热而上浮,但上升的速度不高于0.02m/s,故对模块的冷却效果比较有限。

图6 自然冷却条件下模块附近空气流线图Fig.6 Air Flow Diagram Near the Module Under Natural Cooling
模块的热流(温度梯度)矢量分布图,如图7所示。图中进一步可以证实自然冷却条件下模块向周围环境的散热速率较小,更多的是通过底面固体接触来进行传导散热。

图7 自然冷却条件下模块的热流矢量分布图Fig.7 Distribution of Heat Flow Vectors of the Module Under Nnatural Cooling
3.2 强制风冷条件下的模块热仿真分析
3.2.1 模型的建立与合理性验证
使用空调制冷对模块进行强制风冷,测试空调出风口温度约15℃,冷空气垂直吹向模块的两个大面,流速约0.2m/s。基于上述参数建立强制风冷条件下模块的热仿真模型。
为验证模型的合理性,将模块充满电并以1C倍率恒流放电至单体截止电压3.0V,放电过程采集若干电池单体的壳体表面温度以及室温(Room Temperature,RT)变化,同时采集总负起第1节串联单体的电压,如图8所示。

图8 强制冷却下模块内单体温度随放电时间的变化Fig.8 The Temperature Variety of the Monomer in the Module with the Discharge Time Under Forced Cooling
计算得到放电结束时刻,模块内部各单体表面的温度分布,如图9所示。与自然冷却相比,强制风冷工况下模块的最高温度降低了约3℃,但模块内部的温差由1.5℃左右急剧扩大至5℃以上。故对高比能体系模块进行散热设计时,既需要保证电池的温度不至于过高,又必须充分注意提高温度分布的一致性。

图9 强制冷却条件下模块中截面的温度分布Fig.9 Temperature Distribution of the Cross Section in the Module Under Forced Cooling
1C放电结束时刻不同位置电池单体温度分布的计算值与测量值对比,如图10所示。图中的编号从总负开始。图中可见尽管计算值与测量值存在最大约1.5℃的差距,但二者总体相符,尤其是体现出几乎相同的马鞍形温度分布趋势[7]。模块端部的电池单体温度显著低于模块主体,最大差值在3℃以上,故可适当考虑对端部进行一定的保温隔热处理。
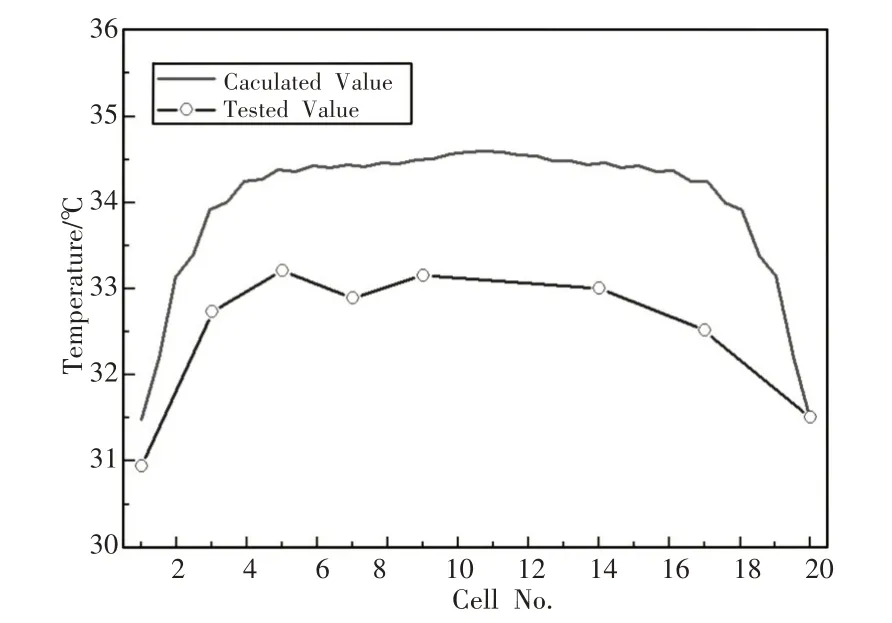
图10 强制冷却条件下各单体温度分布的对比(实验值VS计算值)Fig.10 Comparison of Temperature Distribution of Each Monomer Under Forced Cooling(Experimental Value VS.Calculated Value)
选取总负端起的第3颗电池单体(3#),计算得到的单体温度瞬态变化与实测值的对比,如图11所示。图中计算值和实测值相符的比较好,计算得到的最终温升仅比实测值高1℃。放电中前期计算值温度略高于测量值,这可能是由于采温探头与电池外壳壁面的贴合性不好,不能及时准确地反映壳体的实际温度。

图11 强制冷却条件下3#单体温度分布的对比(实验值VS计算值)Fig.11 Comparison of Temperature Distribution of 3# Monomer Under Forced Cooling Conditions(Experimental Value VS.Calculated Vvalue)
3.2.2 强制风冷的效果分析
取整个计算域的中截面,从不同视角观察模块的温度分布及周围空间冷却空气的流线分布,如图12所示。冷却空气流速矢量图,如图20所示。图12和图13从不同视角直观地显示了强制风冷工况[8]下模块周围冷却空气通过模块表面并经结构件形成绕流的情形,模块的温度分布尤其是角部的温度高低与冷却空气流场密切相关,故针对风冷方式进行合理地优化设计以形成良好的流场分布有助于提升模块的热管理能力。强制冷却条件下模块的热流矢量分布图,如图14所示。与自然冷却条件下相比,散热速率增加了100%以上;且模块除了向底面传热以外,还大量地通过与冷却空气热交换向周围及顶部空间散热。
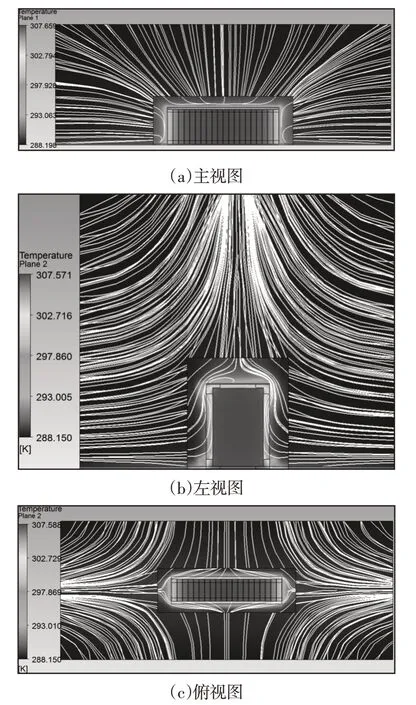
图12 强制冷却条件下模块温度分布及空气流线图Fig.12 Module Temperature Distribution and Air Streamline Diagram Under Forced Cooling

图13 强制冷却条件下模块周围空气流速矢量分布图Fig.13 Air Velocity Vector Distribution Around the Module Under Forced Cooling

图14 强制冷却条件下模块的热流矢量分布图Fig.14 Distribution of Heat Flow Vectors of the Module Under Forced Cooling
3.3 自然风冷和强制风冷的比较以及风冷效费比
研究的2P10S模块1C放电过程的平均产热功率为44.8W,则理想绝热情况下对应的总温升约19.8℃。自然冷却条件下平均总温升约15℃,由此推断平均冷却功率为10W。而考察的强制风冷条件,模块平均温升约11℃,比自然冷却条件降低4℃;平均冷却功率约20W,比自然冷却条件增加了1倍。自然冷却条件下模块内部温差较小,最大温差约1.5℃左右;而考察的强制风冷条件下模块内部的温度一致性显著恶化,最大温差升至5℃以上。上述比较列表,如表1所示。

表1 自然冷却与强制风冷的效果对比Tab.1 Comparison of Natural Cooling and Forced Air Cooling
故如何在提高冷却效果的同时保证各电池单体的温度一致性,是风冷设计最重要的技术关注点之一。
尽管强制风冷比自然冷却能实现更高的模块散热速率,但强制风冷本身也不免需要消耗模块储存的能量。本研究提出强制风冷效费比率的计算公式如下:强制风冷效费比率=100%*(风冷冷却功率-自然冷却功率)/风机耗电功率,其内涵是衡量使用强制风冷手段增加的模块散热能力与风机的电耗之比。模块实际运行过程中的风冷效费比率跟环境温度、充放电倍率(产热功率)、流道设计、风速和风机机械效率等因素相关,同等情况下应追求尽可能高的效费比率。此外,还必须密切关注温度均匀程度,以及客户需求是否要尽可能地控制模块的温度上限。
4 模块风冷技术的优化设计
模块热设计的主要目的是控制温度上限并尽可能地提高各单体之间的温度均匀程度[6]。对风冷而言,最为可行和常用的热设计方式是优化冷却空气的流速、温度和吹入角度[9],故需要合理地设计模块结构并优化风机的控制策略。以流速和温度为例对所研究的2P10S模块进行优化设计研究。
4.1 冷却空气流速的优化
计算得到不同冷却空气流速下模块温度的最大值和最小值变化,如图15所示。总体说来随着冷却空气流速的升高,模块温度不断降低,但最大值和最小值的差距也呈不断增加趋势。由于高比能电池的内阻很小,发热量可以有效地控制在较低的水平,故本例中使用0.5m/s的冷却空气流速就可以将模块的最高温度控制在36℃(309K)以内,最大温差仅为4.5℃左右。在满足模块冷却需要的前提下,选取较小的冷却空气流速,有助于减小风机能耗并降低工作过程的噪音。

图15 冷却空气流速与模块温度分布的关系Fig.15 Relationship Between Cooling air Flow rate and Module TemPerature Distribution
4.2 冷却空气温度的优化
在确定冷却空气流速为0.5m/s的基础上,研究冷却空气温度对模块散热性能的影响。考察的冷却空气温度范围为(17~22)℃(环境温度22℃),计算得到不同冷却空气温度下模块温度的最大值和最小值变化,如图16所示。图中可见,冷却空气温度的降低,有助于减小模块的温升,但同时也不可避免地造成了模块内温差的加大。相对而言,冷却空气为环境温度22℃时,尽管会带来相对更高的温升,但最高温度仅比17℃的冷却空气增加不到1.5℃,同时温差也相应地降低了2℃左右。考虑到使用自然空气进行冷却省却了额外的制冷环节,有利于设备和结构的大大简化,故在本例中推荐直接抽取周围环境内的空气进行风冷,而不必引入车内空调冷风等手段进行散热。

图16 冷却空气温度与模块温度分布的关系Fig.16 Relationship Between Cooling air Temperature and Module Temperature Distribution
经上述不同工况筛选得到的最佳工况条件是冷却空气流速为0.5m/s,温度为环境温度22℃,在该工况条件下,可以在保证模块散热需要的前提下得到尽可能高的电池单体间的温度一致性。
5 结论
(1)使用模块热仿真分析模型对比计算了2P10S三元高比能电池模块不同工况下的冷却效果:自然冷却工况下1C放电结束时刻温升约15.5℃,单体间最大温差在2℃以内;强制风冷工况下温升比自然冷却工况降低约3℃,但单体间最大温差扩大至5℃以上。(2)通过开发的模块热仿真技术对2P10S三元高比能电池模块的强制风冷技术进行了优化设计研究,发现使用流速为0.5m/s、温度为环境温度的冷却空气就可以满足散热的需要,且有助于保持较好的电池单体间温度一致性。
