高墩桥梁施工期风荷载数值模拟计算
2021-06-27刘梦捷蒋明敏
刘梦捷 蒋明敏
(中建路桥集团有限公司,河北 石家庄 050001)
胭脂河大桥位于河北省阜平县胭脂河河谷上,地形的起伏容易使某个区域的风速增大,胭脂河桥址地区为峡谷地形,地形起伏,风环境复杂,风场受地形影响较大。有必要模拟桥址地区的风场并分析。桥梁在施工期,最大悬臂状态下的刚度最小,风对桥梁影响最大,故本文选取研究了桥梁施工期的最大悬臂状态。运用Fluent软件计算胭脂河桥址地区的风场环境数值。通过改变风攻角和得到胭脂河桥梁周围的风场特性,并计算胭脂河桥主梁断面静力三分力系数。
一、数值模拟
(一)静力三分力系数
三分力无量纲化就是三分力系数。静力三分力分为阻力、升力和静力矩。体轴坐标系下的三分力形式,如图1所示。
图1是以桥梁主梁截断面建立坐标系来定义风荷载三分力,但是在桥梁节段风洞试验时,是按照风的来流方向建立坐标系。为了方便,需要将体轴下的静力三分力系数转换到风轴之下,如图2所示。
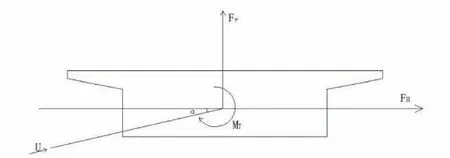
图1 体轴坐标系下三分力
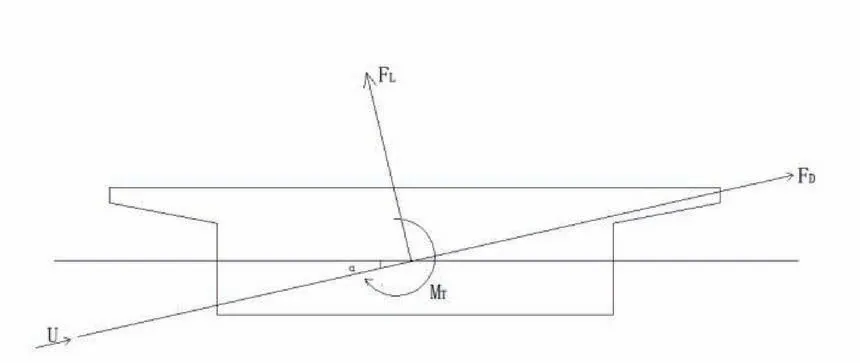
图2 风轴坐标系下三分力
对比发现静力矩在两个坐标系下相同,将风轴坐标系下的三分力表示为升力、阻力和静力矩。那么两个坐标系下的转换关系如式1所示,式中α为瞬时风攻角。

三分力系数转换为单位长度的静力风荷载计算方法如下。
(1)体轴坐标系:
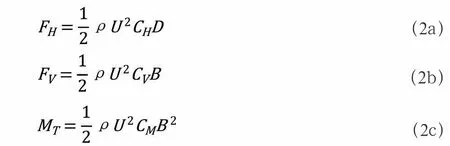
(2)风轴坐标系:

式中U为平均风速;D为主梁断面高;B为主梁断面宽;ρ为空气密度;CH、CV、CM为体轴坐标系下对应的三分力系数;CD、CL、CM为风轴坐标下对应的三分力系数。
(二)数值模型的建立
将地形图文件经过软件处理成可以导入Gambit中的地形曲面,并通过Gambit建立的桥梁模型与之融合。模型建立过程如图3所示,最终得到的桥梁和地形融合模型如图4所示。

图3 模型建立过程
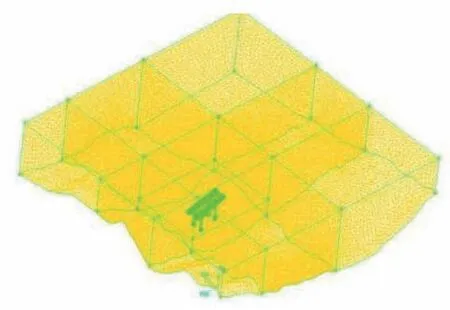
图4 桥梁和地形融合模型
(三)网格划分
考虑到模拟的精确性,经过多次尝试,最终确定了计算域的取值为(1000×1000)m。将计算域划分为9部分,桥梁位于中心块,将中心区域分为上下两层,如图5所示。

图5 网格生成结果
网格划分情况,如表1所示。
表1 网格划分情况
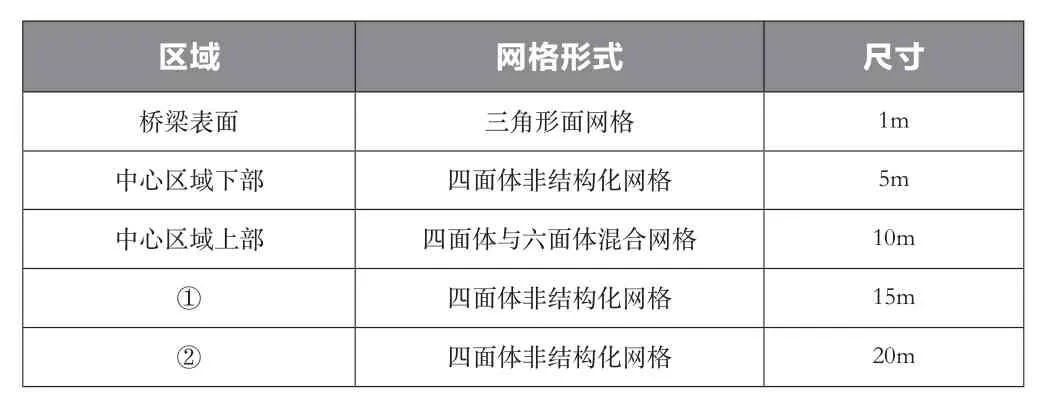
表1 网格划分情况
(四)边界条件
计算域的边界条件设置类型,如表2所示。
表2 边界条件
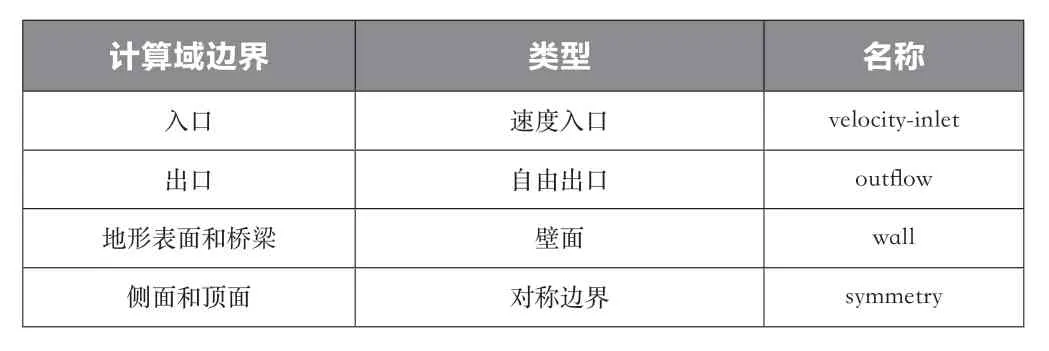
表2 边界条件
二、计算结果分析
通过查询《公路桥梁抗风设计规范》可知河北保定地区的施工阶段设计基准风速22.764m/s。现以22.764m/s的风速作为入口风速模拟风场。通过变化来流风攻角分别为-5°、-3°、-1°、0°、1°、3°、5°,基于Fluent软件研究7种工况下的桥梁主梁截面位置处的风场特性。由于篇幅所限,以悬臂端和悬臂根部为例说明。
(一)压力分布云图分析
悬臂端位置处主梁截面在不同风攻角工况下的风压分布云图,如图6所示。

图6 悬臂端-5°~5°攻角风压云图
如图6所示,主梁悬臂端迎风面承受正压力,上下表面与背风面均为负压。主梁翼缘的右上角,主梁底板右下角流场的回旋区产生较大吸力,主梁背风面和下表面会因为悬臂端风场的绕流形成的漩涡而产生较大的吸力;对比-5°~5°的压力分布云图可以看出,风场会在上表面形成负压区,负压区面积和压力会随着攻角的增大逐渐减小,攻角为-5°时,负压区面积很大,压力最大为-754.131N。当攻角为5°时,负压区面积减小,压力最大为-352.211N。随着攻角由负到正变化,迎风面附近的正压区面积和风压在不断增大,攻角为-5°时迎风面风压最大为589.361N,攻角为5°时迎风面风压最大为901.400N。
悬臂根部位置处主梁截面在不同风攻角工况下的风压分布云图,如图7所示。

图7 悬臂根部-5°~5°攻角风压云图
如图7所示,主梁悬臂根部截面迎风面承受正压力,上下表面与背风面均为负压,由于桥墩对风场的阻挡作用,流场的绕流作用会在桥墩周围形成很多漩涡,在悬臂根部截面周围形成范围很大的负压区。主梁翼缘的右上角,主梁底板右下角及主梁背风面会因为流场的回旋区产生较大吸力;对比-5°~5°的压力分布云图可以看出,风场会在上表面形成负压区,负压区面积和压力值会随着攻角的增大逐渐减小,攻角为-5°时,负压区面积很大,压力最大为-704.233N。当攻角为5°时,负压区面积减小,压力最大为-312.371N。随着攻角由负到正变化,迎风面的正压区面积和风压在不断增大,攻角为-5°时迎风面风压最大为563.702N,攻角为5°时迎风面风压最大为841.233N。
(二)速度流线图分析
悬臂端位置处主梁截面在不同风攻角工况下的风速流线图,如图8所示,风场在主梁悬臂端截面表面速度较小,流线在迎风面的棱角处分散,产生了漩涡,形成回旋区,对上翼缘板产生吸力。悬臂根部截面从迎风面到背风面的风场呈现不断衰弱的变化趋势,在背风面留下范围很大的尾流区,而且风速很小,尾流区气流在移动过程中不断有漩涡脱落。

图8 悬臂端-5°~5°攻角风速流线图
对比悬臂端截面不同攻角下速度流线,流线在迎风面处出现分散现象后,攻角为负时气流会较早在箱梁顶板上附着。不同攻角下最大风速均出现在迎风面的上翼缘板右上角,当攻角为-5°时风速最大,为33.253m/s。这是由于攻角为正时,翼缘对风速有阻挡作用而导致风速有所减小。
悬臂根部位置处主梁截面在不同风攻角工况下的风速流线图,如图9所示,风场在主梁悬臂根部截面表面速度较小,流线在迎风面的棱角处分散,产生了漩涡,形成回旋区,对上翼缘板产生吸力。悬臂根部截面从迎风面到背风面的风场呈现不断衰弱的变化趋势,由于桥墩对风的阻挡作用,在背风面留下范围很大的尾流区,而且风速很小,尾流区气流在移动过程中不断有漩涡脱落。

图9 悬臂根部截面-5°~5°攻角风速流线图
对比悬臂根部截面不同攻角下的速度流线,流线在迎风面处出现分散现象后,攻角为负时气流会较早在箱梁顶板上附着。不同攻角下最大风速均出现在迎风面的上翼缘板右上角,当攻角为-5°时风速最大,为28.350m/s。这是由于攻角为正时,翼缘对风速有阻挡作用而导致风速有所减小。
(三)静力三分力系数计算
悬臂端和悬臂根部在不同风攻角下的静力三分力系数值如表3所示。
表3 不同风攻角下静力三分力系数
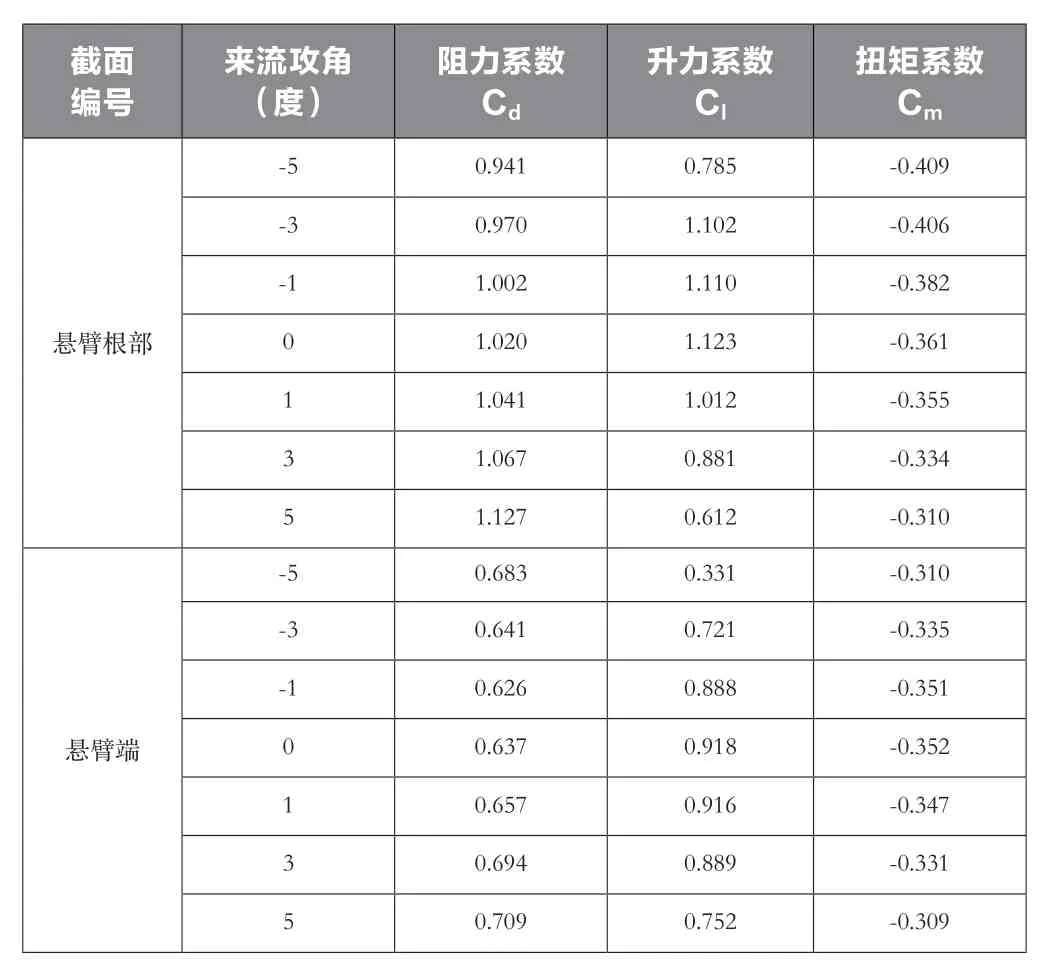
表3 不同风攻角下静力三分力系数
运用Matlab软件拟合三分力系数与攻角关系,悬臂根部三分力系数对比图,如图10所示,悬臂根部截面的阻力系数随着攻角由-5°~5°变化不断增大。悬臂根部截面的升力系数在风攻角由-5°~0°变化时随着风攻角的增大而增大,然后在风攻角为0°附近取得最大值,风攻角由0°~5°变化时升力系数随着风攻角的增大而逐渐减小。悬臂根部截面扭矩系数随着攻角由-5°~5°变化不断增大。
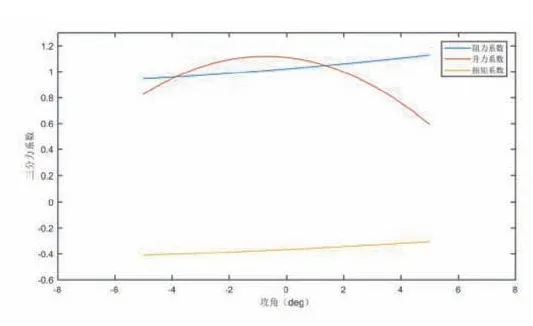
图10 悬臂根部三分力系数对比图
由图11可以看出阻力系数随着攻角由-5°~5°变化,先是不断减小,在0°攻角附近取得最小值,然后再逐渐增大;升力系数在风攻角由-5°~0°变化时随着风攻角的增大而增大,然后在风攻角为0°附近取得最大值,风攻角由0°~5°变化时升力系数随着风攻角的增大而逐渐减小;扭矩系数随着攻角由-5°~5°变化而不断增大,悬臂端截面扭矩系数在攻角-5°~0°不断减小,在攻角0°取得最小值,在攻角0°~5°不断增大。将CFD模拟值与拟合曲线对比发现拟合结果较准确。

图11 悬臂端三分力系数拟合图
经过对比8个节段的截面三分力系数发现,升力系数随风攻角的变化较大,阻力系数和扭矩系数随风攻角变化不大。阻力系数受梁截面高度影响较大,截面高度高会使得截面与风的接触面积较大,承受的风荷载也较大,阻力系数值也相对较大。梁高的变化对升力系数和扭矩系数影响较小,所以两个截面的升力系数和扭矩系数也相对较为接近。
三、结语
本文通过模拟计算,得出相关结论:
1.风场会在箱梁的上下表面及背风面形成负压区,且上表面的负压区随着攻角的增大而不断减小。
2.风攻角为5°时,箱梁迎风面风压最大,最大风压出现在箱梁截面右上角。
3.三分力系随攻角的变化规律大致符合一元二次函数,悬臂根部截面与最大悬臂端截面的三分力系数随着风攻角变化的规律是相近的,升力系数随风攻角的变化较大,阻力系数和扭矩系数随风攻角变化不大。
4.对比不同箱梁节段截面的三分力系数发现,阻力系数受梁高影响较大,随着梁高的增大而增大。
