城市旧房改造初期居民与政府的演化博弈分析

■ 吴伟东 张琳 景奕杰 姚灿 许博浩

西南石油大学土木工程与测绘学院 成都 610500

0 引言

在城市化建设发展过程中，由于土地资源的稀缺，导致我国走外延式城市发展道路存在很大的局限性[1]，另一方面，又因为城市老旧住宅可通过加固结构性能、完善基础设施和修复环境功能等措施[2-4]，从而实现城市土地资源的节约、城市功能布局的完善、城市形象的提升、群众居住条件的改善以及居民生命财产的安全[5,6]。另外，在国家层次方面，党中央从2018年到2020年相继召开的“第十三届全国人大一次会议、二次会议和三次会议”也指出，旧房改造是改善居民居住环境条件、扩大城市内部需求以及促进城市经济发展的重要举措[7-9]。然而，随着我国旧房改造的落地实施，政府面临的资金压力、部分居民对旧房改造表现出的消极态度等问题日益突显，这也是我国未能快速推动旧房改造的重要原因[10]。因此，如何在减轻政府经济压力的同时，提升居民的积极性和实现政府与居民的利益平衡，是目前推进旧房改造落地实施的重要问题。

在1991年，国务院公布了我国首部实施旧房改造的依据—《城市房屋拆迁条例》，旧房改造便引起了建筑领域研究学者的关注，同时，也有相关学者开始对旧房改造进行研究。通过对这部分相关学者的研究成果进行收集，发现该部分研究主要集中在“改造前”与“改造后”两个维度：（1）对于“改造前”的相关准备工作，陈科迪总结了未进行改造的旧建筑所存在的问题及解决办法[11]；冉浩然和李峻峰、周松柏等人分别分析了影响旧住宅区进行改造的关键社会因素和环境适宜性因素[12-14]；任绍斌提出了在遵守公平性、全局性和伦理性的基础上进行城市更新的规划策略[15]；（2）对于“改造后”的相关评价研究，汪达尊、陈庆玲和王建认为旧房改造后的房屋建筑更具有经济性，符合我国的可持续发展战略[16-18]；Li 提出了经过旧房改造后的建筑在结构安全性、建筑外观、室内舒适性方面均得到不同程度的提高[19]；杜新栋则认为组合加固技术与老旧建筑的稳定性更为契合[20]。

通过以上研究可以发现，各学者仅对影响旧房改造的某一客观因素进行了研究分析，却没有考虑到在城市旧房改造初期，在有限理性且能够考虑到的各种客观因素的共同作用下，居民与政府要达到怎样的利益平衡，才能够推动旧房改造的进行。因此，本文以旧房改造相关主体的利益关系为背景，使用演化博弈的方法，建立“政府-居民”的动态演化博弈模型，通过仿真模拟对模型进行验证，并对演化路径进行分析，最终提出解决政府在旧房改造初期所面临的资金压力、部分居民的消极态度、利益分配不平衡等问题的稳定策略，以期提升群众对政府的信任感和实现政府与居民的利益共赢，为政府推进城市旧房改造的发展提供理论支持。

1 旧房改造初期演化博弈模型构建

1.1 演化博弈理论

博弈论又称为对策论，是研究博弈主体行为策略选择以及策略在受到其他主体影响时达到均衡状态的一门社会学分支理论。演化博弈论是以经典博弈论为基础，将博弈思想和动态演化现象相结合，研究有限理性的群体在重复的博弈过程中不断模仿和学习来调整自身策略，最终达到最优策略的动态均衡[21]。

1.2 政府-居民的演化博弈

1.2.1 模型假设

以下假设均满足以上条件：①文中的“该区域”特指达到国家颁布的“旧房改造”政策条件的区域；②若要进行改造，居民需要出小部分资金（本文特指建筑物内的部分共用部位和公用设施），政府出大部分资金；③文中的“居民”是指待改造区域的“绝大部分居民”。

（1）政府在考虑所在区域大环境下的经济、社会等方面的需求的情况下可将该区域规划为旧房改造区域的概率为y（意味着政府要耗费大量资金在旧房改造的项目上），则不将该区域划分为旧房改造的概率为1-y；居民在考虑自身经济或心理生理接受程度等情况下，若居民有意愿对该区域进行改造的概率为x，则无意愿改造的概率为1-x。

（2）对居民-政府演化博弈的相关参数做出假设，具体含义如表1所示。

表1 政府-居民演化博弈中的参数假设

1.2.2 演化博弈模型分析

依据上述假设条件，可得出政府-居民的博弈矩阵模型，如图1所示。

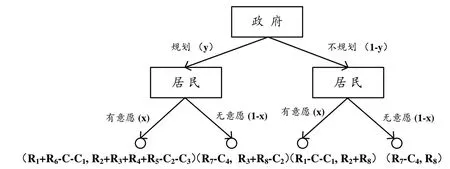
图1 政府-居民模型博弈树

政府把该区域规划为旧房改造区域和不规划为旧房改造区域的期望U(y1)和U(y2)，以及政府的平均期望收益(y)分别为：

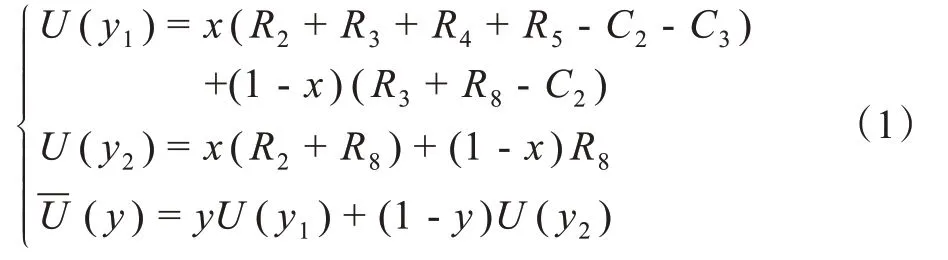
居民对旧房改造有意愿和无意愿的期望U(x1)和U(x2)，以及居民的平均期望收益(x)分别为：

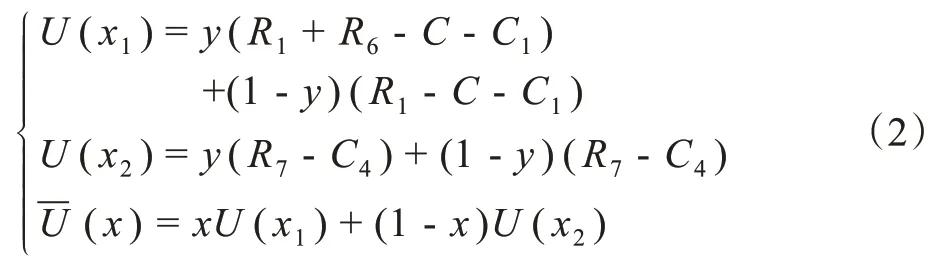
如上方程（1），（2）可得到政府将该区域规划为旧房改造区域与居民对旧房改造有意愿的复制动态方程为：

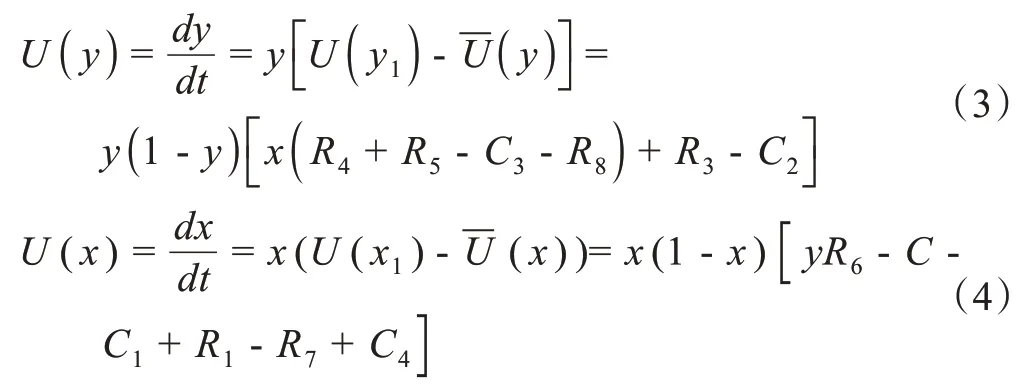
若要使居民和政府在博弈中稳定的进化，方程式（3），（4）必须满足：

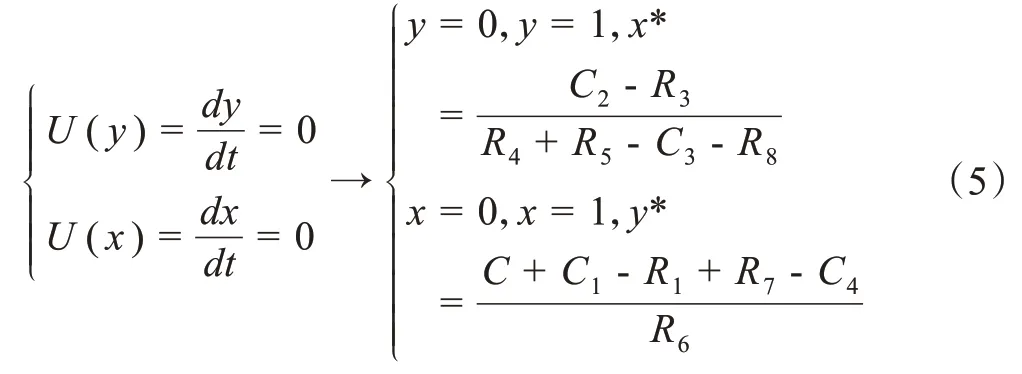
则可得出政府和居民博弈矩阵的5 个局部平衡点为：

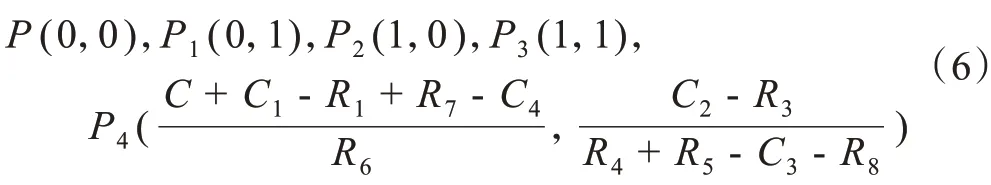
根据演化博弈动态方程的稳定性原理和性质，该演化均衡策略的动态方程应满足：U(x) = 0,U'(x) < 0。政府和居民复制动态分表如表2和表3所示。

表2 政府复制动态分析表

表3 居民复制动态分析表

1.2.3 结果分析

若要使政府把该区域规划为旧房改造区域的情况下，居民也对旧房改造有意愿，使其达到最优均衡状态，就应使和y* =尽可能取最小值。则可以有效的增大：①政府的社会效益R3、经济效益R4和生态效益R5；②居民提升的心理、生理舒适度R1；③居民获得的老旧房寿命价值增长效益R6；④未改造前居民的原有基础设施使用成本C4。也可以减小：①居民进行改造的部分共用部位与公共设施的费用C和改造后居民的基础设施使用成本C1；②政府的组织建设与宣传成本C2和政府对待改造区域所要支付的设计、施工和临时占地费用C3。

2 旧房改造实施策略的仿真模拟分析

本文使用MATLAB8.1.0对“政府-居民”演化博弈模型进行仿真模拟，预测政府和居民在面对不同程度的收益与支出情况下的选择策略效果，并对模拟出来的结果进行分析。

以横轴为时间轴，用t表示，设定其时间范围为0～10。以纵轴表示可进行旧房改造的概率Q，设定其时间范围为0～1。设政府与居民一开始就达成同意旧房改造的一致性意见的概率Q为0.4，模拟分析的初始参数如表4所示。在对某个参数进行相应的变化讨论时，除特别指定外，其余参数均不发生改变。

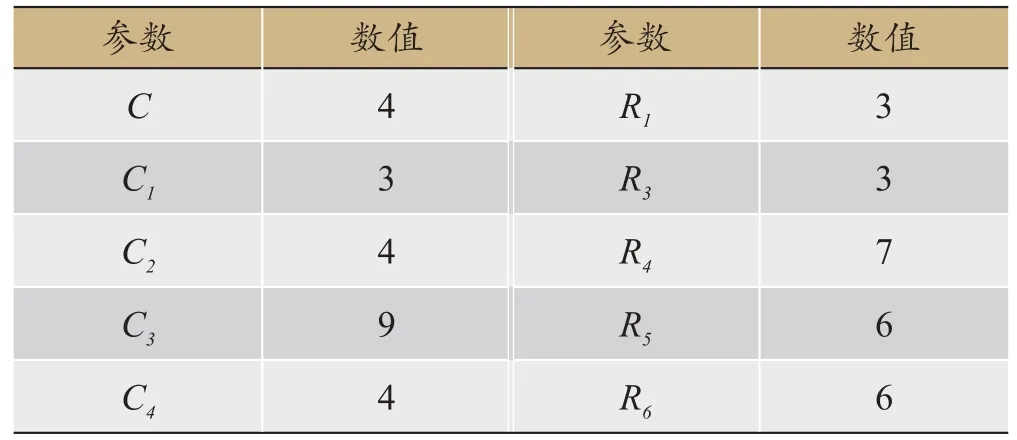
表4 参数初始值

（1）政府在旧房改造时获得的社会效益R3、经济效益R4和生态效益R5的变化对演化路径的影响。

当初始值R3=3，R4=7，R5=6,再对R3取值为1,5；R4取值为4,10；R5取值为4,7时，对该区域进行旧房改造策略选择的演化路径进行模拟，结果如图2所示。

由图2可以看出，当R3从1→5，R4从4→10，R5从4→7时，政府对旧房改造的演化路径从走向“0”的趋势逐渐走向“1”，说明政府对旧房进行改造可获得的社会效益、经济效益和生态效益越高，政府对该区域进行旧房改造的概率越高。当1＜R3＜3，4＜R4＜7，4＜R5＜6时，各均存在一个平衡点，使得政府对该区域从“不改造”走向“改造”的演化。

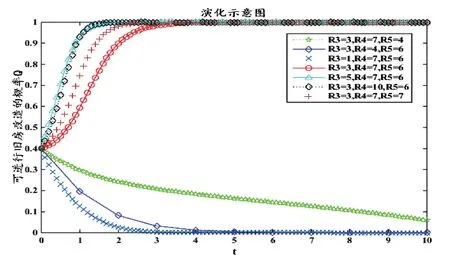
图2 R3、R4和R5值变化影响仿真模拟图

（2）政府把该区域划分为旧房改造区域时，政府需对该次旧房改造的政策宣传与组织建筑的成本C2和对该区域支付的设计、施工和临时占地费用等的费用C3的变化对演化路径的影响。

当初始值C2=4和C3=9，再对C2进行取值为2,6；C3取值为4,14时，对政府是否将该区域划分为旧房改造区域策略选择的演化路径进行模拟，结果如图3所示：

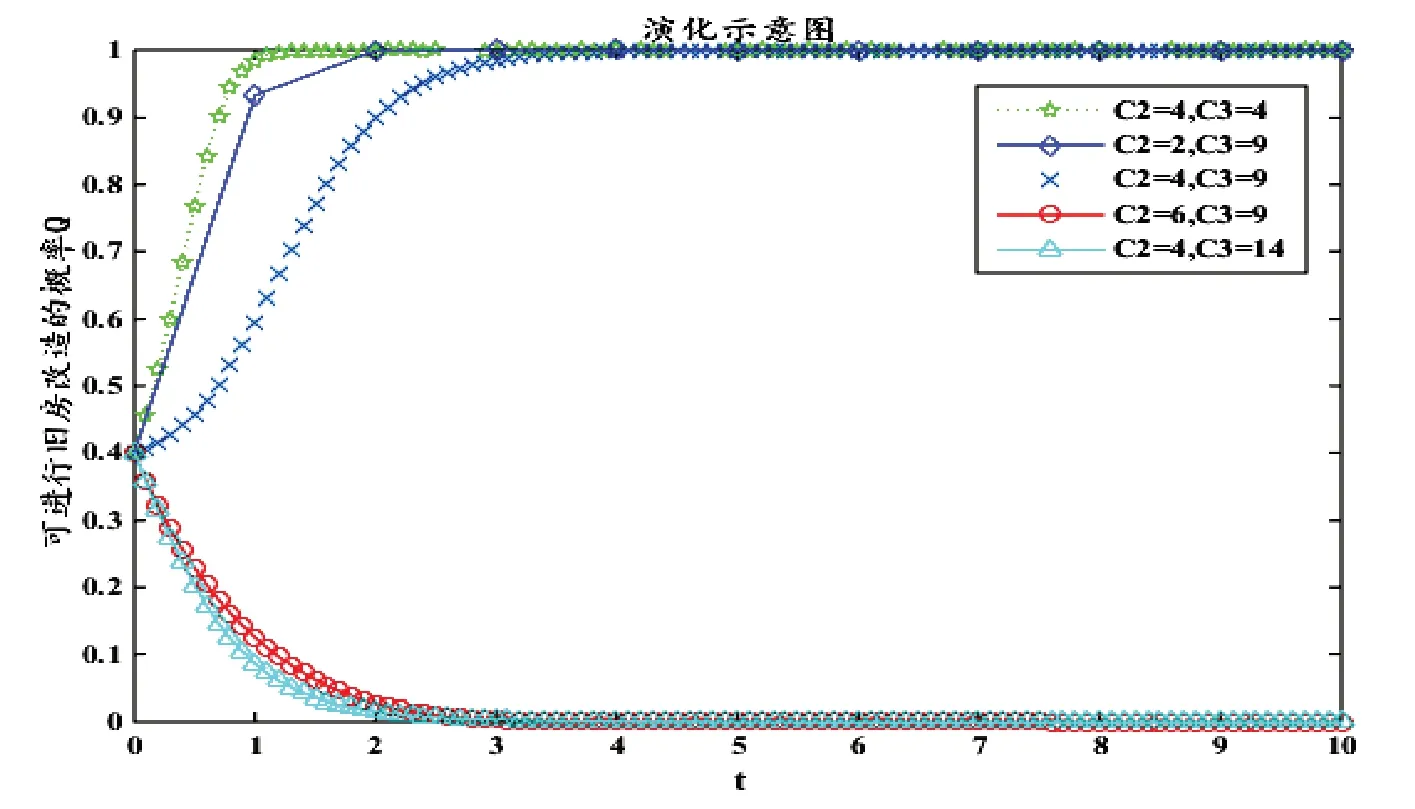
图3 C2、C3值变化影响仿真模拟图

由图3可以看出，当政府对组织建设、政策宣传和设计、施工与临时占地等的成本C1、C3越低，政府对该区域进行旧房改造的概率Q越高。当C2=2和C3=4时，政府对该区域进行改造的演化路径走向“1”的速度快于当C2=4和C3=9时。当4＜C2＜6、9＜C3＜14时，各均存在一个平衡点，使得演化路径从不改造“0”走向改造“1”的演化。

（3）居民对旧房改造有意愿时，需承担的共用部位与公用设施的费用C和改造后建筑体内的生活基础设置使用成本C1的变化对演化路径的影响。

当初始值C=4和C1=3，再对C进行取值为1,7；C1取值为1,5时，对居民是否有意愿进行旧房改造策略选择的演化路径进行模拟，结果如图4所示：

由图4可以看出，若居民需要对旧房改造建筑体内的共用部位和公用设施的费用C和改造后生活基础设施使用成本C1越高，则居民对旧房改造的意愿越低。当C=7、C1=5时，演化路径最终走向“0”。

图4 C、C1值变化影响仿真模拟图

（4）政府将该区域规划为旧房改造区域，且居民对旧房改造有意愿时，居民的心理、生理舒适度提升的价值R1和居民可获得的老旧房寿命增值的效益R6的变化对演化路径的影响。

当初始值R1=3和R6=6，再对R1进行取值为0.5,5.5；R6取值为1,11 时，对居民是否有意愿进行旧房改造策略选择的演化路径进行模拟，结果如图5所示：

由图5可以看出，当居民对旧房进行改造可获得的心理、生理舒适度提升价值R1和老旧房寿命价值增长的效益R6越高，居民对旧房改造的意愿越强烈，则演化路径向“1”的方向演化的越快。当0.5＜R1＜3、1＜R6＜6时，各存在一个平衡点，使得演化路径从“不改造”走向“改造”。

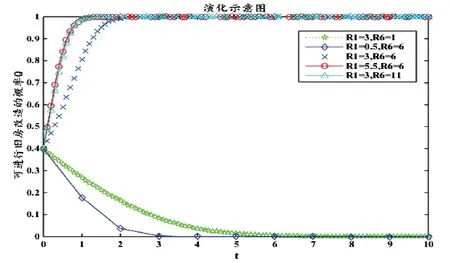
图5 R1、R6值变化影响仿真模拟图

（5）居民对旧房未进行改造时，原有的基础设施使用成本C4的变化对演化路径的影响。

当在C4=4的初始值基础上分别再取值为0.5,2,6,7.5时，对居民是否改变意愿进行旧房改造策略选择的演化路径进行模拟，结果如图6所示：

由图6可以看出，当未进行改造的原有旧房基础设施使用成本C4越高，为了减少长期支出，则居民进行旧房改造的概率Q便会越高。当2＜C4＜4时，存在一个居民从无意愿改造走向有意愿改造的平衡点，若C4越大，居民向着旧房改造的方向演化速度越快，当C4=7.5时，演化速度最快，且最终走向“1”。

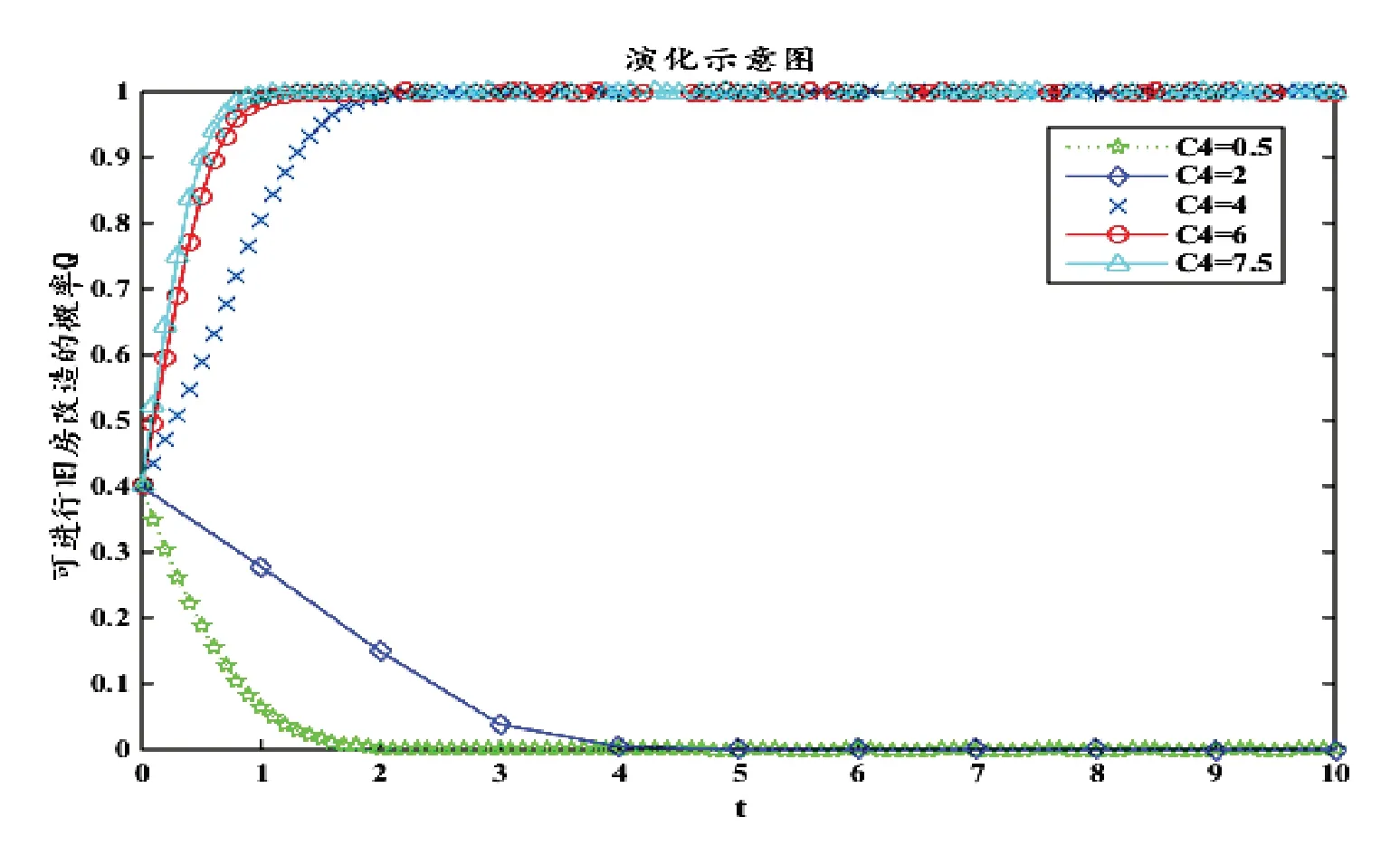
图6 C4值变化影响仿真模拟图

3 结论与对策建议

3.1 结论

本文创新性的运用演化博弈方法探索旧房改造初期居民与政府的策略选择，并对所选策略的演化路径进行仿真模拟分析，通过研究得出：

（1）政府与居民通过旧房改造获得的利益越高，则政府和居民进行旧房改造的概率就越大；

（2）政府与居民对是否进行旧房改造的决策选择受到“原始成本”（不进行旧房改造时需付出成本）和“改造成本”（进行旧房改造时需付出的成本）的影响，即“原始成本”越高，则政府与居民进行旧房改造的概率就越大；“改造成本”越高，则政府与居民进行旧房改造的概率就越小。

（3）考虑到政府与居民资金投入量大与资金有限性的矛盾（尤其是政府），资金成本的投入只需满足从“不改造”走向“改造”的平衡点便可以实现旧房改造，这样既可以满足旧房改造的顺利进行又能节约成本，实现资金的有效利用；

（4）居民对旧房改造的意愿受到心理因素（主观认识）和生理因素（客观需求）的影响。

3.2 对策建议

基于以上结论，为最终实现帕累托最优均衡和政府与居民的利益共赢，本文主要提出如下几个方面的对策建议：

3.2.1 加强资金有效投入，做好成本规划控制

（1）政府应当充分利用待改造区域还能正常运作的原有市政设施（如市政排水管道、天然气管道、电力、通讯等设施）和配套设施（中小学、幼儿园、医院等场所），减少政府市政工程及配套项目的费用支出，减轻经济负担。

（2）政府作为旧房改造资金来源的主要供给者却不得不面临资金支出的有限性，因此，扩大社会资金来源是解决该问题的有效措施，如政府对居民旧房的主体结构工程进行修护、加固和美化的同时引导企业或金融机构参与到该区域绿化环境建设改造和配套设施改善、新增修建中，以改造后该区域的经济收入按一定份额给予社会资本作为成本支出的补偿等。

（3）政府应当为居民制定高效的资金投入计划，并表明资金使用期间给予居民资金流向清单说明，做到“一分钱一分货”，让居民充分意识到该部分资金投入的合理性与必要性，以此提升居民出资意愿的积极性。

3.2.2 建立健全信息机制，促进改造“软性”管理

（1）政府应当适当有效的对旧房改造政策进行组织宣传、设立听证会，使得居民对旧房改造的计划与相关政策有足够的了解和有权表达合理的意见（如后期可通过问卷调查的方式回收居民的对旧房改造的理解、意愿与建议），提升居民的社会责任感与对政府的信任度，从而避免旧房改造过程中可能造成的社会矛盾。

（2）更新旧房改造区域服务体系，为居民带来更为便捷的生活环境，提升居民的生理和心理的满意度与幸福度。

3.2.3 完善改造规章制度，加强过程监督管理

（1）加强对旧房改造规章制度的完善和对各部门的职能明确划分，做到有法可依，提升工作执行效率，改善改造程序繁琐和改造周期长的弊端，最终实现高效工作、缩短工期以达到政府和居民成本节约的目的。

（2）主动接受人民群众监督，使得改造过程透明化，有效提高政府行政管理水平和工作效率，将人员安全、房屋财产安全及国家社会利益放在第一位，赢得居民的信任，促进旧房改造的顺利进行。