An image encryption algorithm based on improved baker transformation and chaotic S-box∗

Xing-Yuan Wang(王兴元), Huai-Huai Sun(孙怀怀), and Hao Gao(高浩)

School of Information Science and Technology,Dalian Maritime University,Dalian 116026,China

Keywords: image encryption,improved baker transformation,chaotic S-box,chaotic sequence

1. Introduction

With the continuous development of computer network technology,the confidentiality of network information has attracted more and more attention. Because digital images have the advantages of long-term preservation,multiple replication,and easy transmission, they have gradually become the main way for people to obtain information on the network. However, there are also hidden dangers. Mainly because the image involves a lot of information, it is easy to be stolen in the transmission of the network, thereby bringing great trouble to people. Due to the rapid development of the network,it is possible for one to collect the digital image information in the network.[1]Therefore,it is extremely important to transmit digital image information over the network to ensure its security. Nowadays, many image protection schemes have been proposed, such as encryption, watermarking, steganography,and other methods.[2–4]For image encryption,designing a safe and effective encryption algorithm has become an inevitable option. Since the classical encryption algorithm does not take into account the inherent characteristics of large data capacity and high redundancy of images,these algorithms are not suitable for image encryption. Chaos is not only a new form of existence in nonlinear dynamic systems, but also closely related to fractals in nonlinear science. It can be said that chaos is the fractal of time, and fractal is the chaos of space.[5–7]In the chaotic image encryption algorithm used cleverly are the initial conditional sensitivity, pseudo-randomness, ergodicity, and reproducibility of the motion law of the chaotic system. These properties can meet the requirements for the security sensitivity characteristics of encryption algorithms.Based on this, many researchers home and abroad have proposed many efficient and secure chaotic image encryption algorithms. Chaos-based image encryption algorithms have become a research hotspot.

In general, chaotic-based image encryption algorithms mainly include two steps: scrambling of image pixel positions and diffusion of image pixel values. At present,common image scrambling methods cover scrambling methods based on Arnold transform, magic square transform, and baker transform. The baker transformation method is a transformation technique that stretches and folds continuous planar regions.[8]Applying the traditional baker transformation method to the image scrambling, if the number of transformations is unreasonable,it will get a bad scrambling effect. In addition,when the continuous plane area processed by the conventional baker transformation method is too large, there is a disadvantage that the transformation randomness is poor and the transformation time is long. Therefore, this article proposes an improved method of applying the baker transformation to the image scrambling stage. The encrypted image is divided into 16 small blocks on average, and the image is scrambled by using a conventional baker transform method for each block,and the number of transformations is controlled by the chaotic sequence,so that the scrambling effect is more random. In addition,the S-box is a module that plays a central role in a block cipher system, and mainly plays a role of confusion and proliferation. The security strength of the S-box determines the security of the encryption algorithm. Traditional cryptography uses algebraic methods to construct the S-box. Although a high degree of nonlinearity can be obtained, the differential performance is relatively weak due to the simplistic structure and cannot resist algebraic attacks.[9,10]The application of chaotic systems to the design of nonlinear S-box is more effective. Based on this, this paper cites the chaotic S-box designed in Ref.[11]to process the encryption key of the algorithm. Therefore,the main contribution of this paper lies in proposing a new chaotic image encryption algorithm. In the algorithm,the improved baker transformation and chaotic Sbox are utilized. Experimental results prove that the algorithm proposed in this article is more efficient and safer.

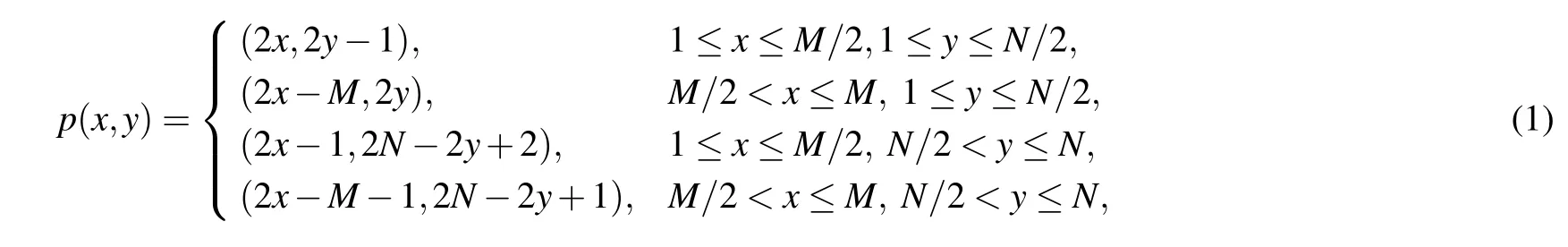
The rest of this article is organized as follows. In Section 2 presented is the initial preparation,describing the theoretical knowledge and chaotic systems used in the algorithm.In Section 3 given is an algorithm description that describes the encryption process of the algorithm and comes with an encryption flowchart. In Section 4 the results of the simulation experiment are provided. Several digital images are selected and the simulation results are presented. In Section 5 analyzed is the security of the algorithm from various attack methods.In Section 6,some conclusions are drawn from the present study and the direction of future work is also suggested.

2. Initial preparation work

2.1. Improved baker transformation

In fact,the baker transformation can produce stretch-like and folding effects in the state space,just like a baker rubbing a piece of dough.Imagine that adding a blue food colorant to the dough,which is repeatedly stretched and folded by the baker,the blue color is evenly mixed in the dough. The stretching and folding mechanisms cause adjacent points to eventually separate in an exponential manner,creating a sensitive dependence on the initial state. Therefore,the baker transformation has chaotic dynamic characteristics,and thus very much suits an image scrambling method.[12]

In this paper,a baker discrete transformation method for data dot matrix scrambling of digital images is designed and described as follows:

where the plain imageAM×Npixel value is represented byp(x,y). An example of a traditional baker transformation is shown in Fig.1.

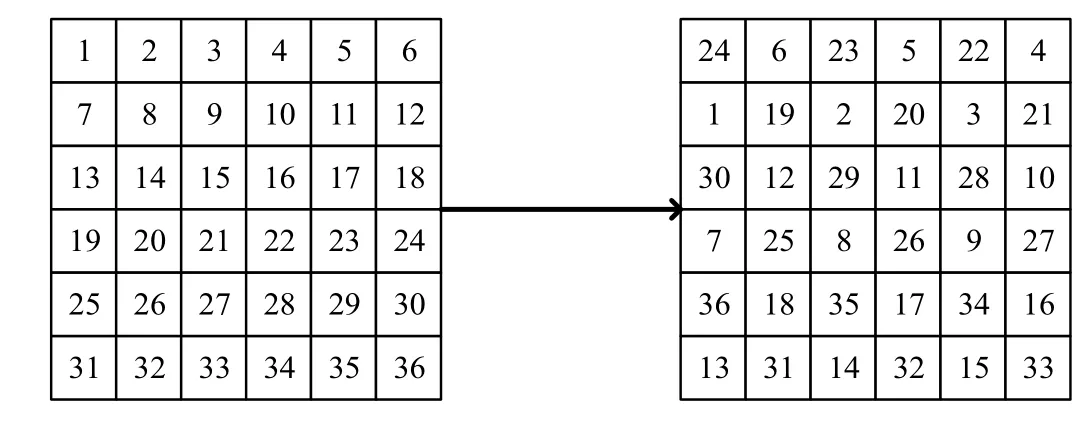
Fig.1. Traditional baker transformation process of 6×6 matrix.

It can be seen that there are certain limitations to applying the traditional baker transformation to the image scrambling.On the one hand, when the number of transformations is too small,the visual scrambling effect is not good. In Ref.[12],it was proved experimentally that the original image is unrecognizable when the number of transformations exceeds 4 times;on the other hand, the continuous plane area of processing is very large,and there will be disadvantages such as long timeconsuming and poor randomness of scrambling. Therefore,in this paper the traditional baker transformation is improved to some extent. On the one hand, the original image is divided into multiple blocks,and each small image is separately transformed into a traditional baker, and finally each small image after being scrambled is spliced into a scrambled image.In addition,the number of times the Baker transforms is controlled by the chaotic sequence, so that the number of times of each small image transformation is different,so the scrambling randomness is better.

2.2. S-box description

In general, the S-box is also known as the replacement box. It is a nonlinear transformation tool. There are three main methods of constructing the S-box. They are stochastic construction methods,mathematical construction methods,and a combination of the two methods.[13,14]In actual use, it can be considered that the S-box is a Boolean map, and the S-box of sizeM×Nhas the formFM2→FN2,that is,the data of the number of bitsMare input to the S-box,and the data of theNbits are output. TheM-bit data change nonlinearly and can become seemingly randomN-bit data.[15]

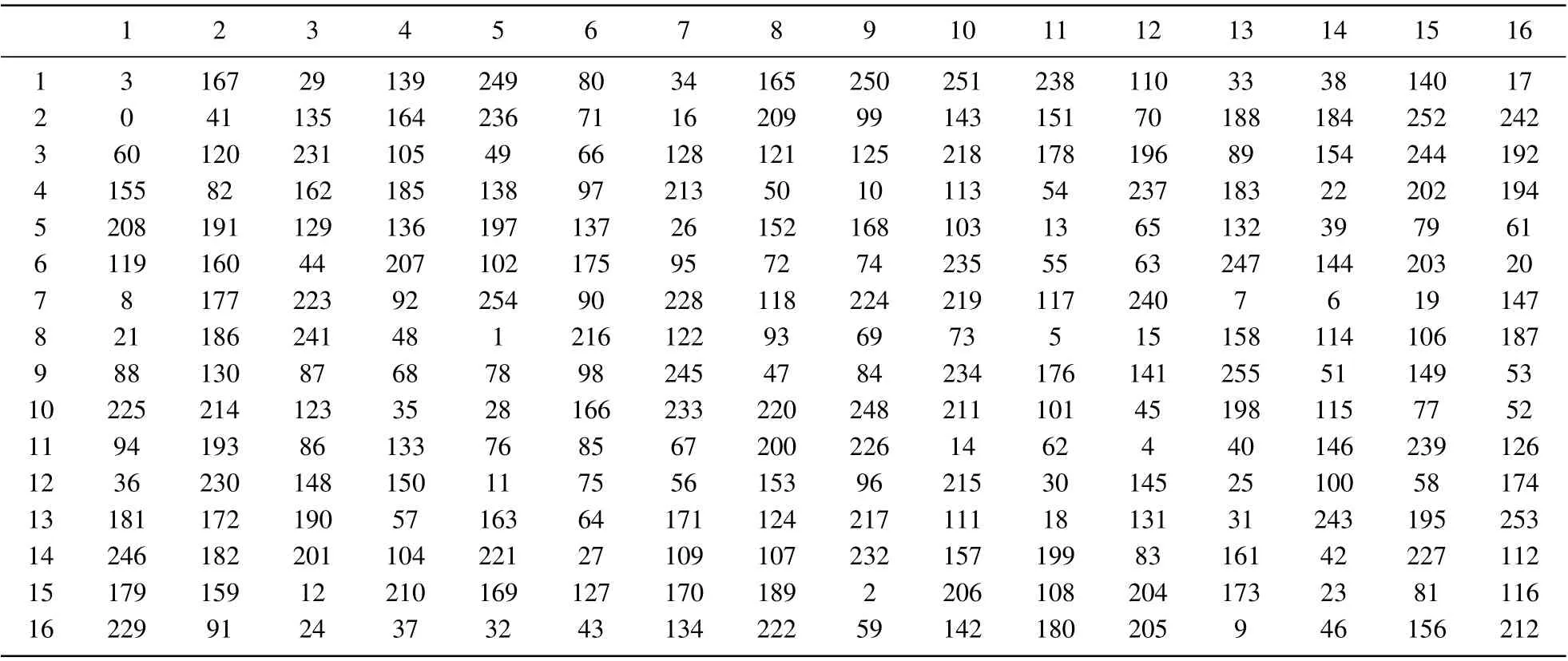
Table 1. 16×16 matrix representation of S-box.

In addition,applying the chaotic system to the design and generation process of the S-box will achieve more desirable results. Khanet al.[11]proposed a robust S-box construction technique based on the chaotic Lorenz system.This S-box can effectively eliminate the need of using a separate key in the scrambling diffusion structure, and the generated S-box has an ideal nonlinear performance. Simulation experiment analysis shows that the S-box has a good encryption performance.The chaotic S-box discussed in Ref.[11]is cited in this paper,and its compositions are shown in Table 1.

2.3. Chaotic system

The one-dimensional logistic mapping is a typical nonlinear iterative equation. The equation is as follows:

where the logistic mapping system is in a chaotic state when 3.5699＜u ≤4,xkrefers to the iterative state value, defined between consecutive real fields from 0 to 1,andx0is the iteration initial value.For a given initial valuex0,the sequence generated under the action of Eq.(2)is aperiodic,non-convergent and sensitive to initial conditions. Because the logistic mapping is a simple nonlinear one-dimensional discrete iterative mapping, it is easy to implement in hardware. So it has become one of the most widely used chaotic maps in digital chaotic systems.[16–18]

3. Algorithm description

The encryption algorithm proposed in this paper has the same encryption steps as most of previous algorithms,that is,image processing, scrambling and diffusion of images. Because the security and effectiveness of the proposed algorithm should be strengthened, different encryption keys are used in different image encryption stages. Aiming at the encryption algorithm proposed in this paper,the specific implementation process is presented as follows.

3.1. Image processing

The image encryption algorithm proposed in this paper and most of previous algorithms have the same requirements for image sizes,that is,the original encrypted image is in the form of a square matrix.In other words,for a pair of grayscale digital images of sizeM×N,M=Nis required.IfM/=N,the method of zeroing the original image is taken,so that the number of rows and the number of columns of the original image are equal.

3.2. Scrambling process

Step 1 Enter the keysa0andu1, and substitute the two into the formula of the logistic chaotic map. The 1000 iterations eliminate the transient effects. After 16 consecutive iterations, the obtained chaotic sequence is recorded asai(i=1,2,...,16). The substitution of a chaotic sequenceaiof length 16 into Eq. (3) yields a one-dimensional sequencea＇i(i=1,2,...,16).

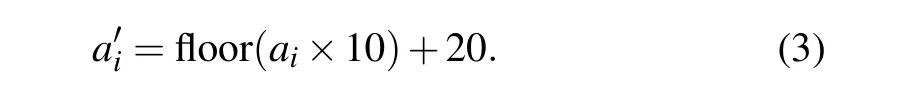
Step 2 The original imagePis divided into 16 subimages according to the rank and column average. The sub-image obtained after the division is recorded aspi(i=1,2,...,16).The baker transformation is performed separately for each small image, and the number of baker transformations is controlled by the one-dimensional sequencea＇i.The 16 small images obtained by the baker transformation are sequentially spliced into a large decrypt image,which is recorded asP1.

Step 3 Similarly,the keysb0andu2are substituted into the formula of the logistic map. The 1000 iterations eliminate the transient effects. After continuing to implementM×Niterations, the obtained chaotic sequence is recorded asbi(i=1,2,...,M×N). And the substitution ofbiinto Eq. (4)yields

where sort(·) represents the sorting function. Using the sorting function,the corresponding subscript of each value in the sequenceb＇in the sequencebis stored as the sequenceD. A scrambled arrangement in whichDis a sequence of integers from 1 toM×Ncan be obtained. The imageP1,from the first pixel point to establishP1itoPDimapping. The positions are exchanged from the first element to the last element one by one. After that, imageP1is converted into imageP2with a size ofM×N.

At this point, the scrambling process for the encrypted image is completed.

3.3. Diffusion process

Step 1 First,enter the keysx0andu3,and substitute the two keys into the logistic chaotic mapping formula. The 1000 iterations eliminate the transient effects. ThenM×Nconsecutive iterations are implemented. The chaotic sequencexi(i=1,2,...,M×N) is obtained and substituted into the following formula:

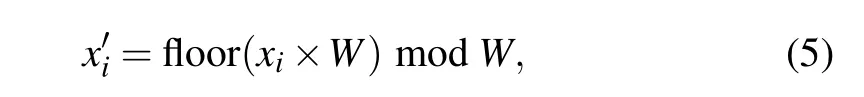
whereW=max(M,N). Thus,a one-dimensional sequencex＇iis obtained,and the sequence length isM×N.

Step 2 Let key0=floor(Pmean)+R,where key0refers to an initial key in the encryption process,Pmeanrepresents an average pixel value of the imageP,andRis a given integer. The initial key key0converted from a decimal number to an 8-bit binary number is still denoted as key0.

Step 3 Take the 3rd to 6th digits of the 8-bit binary number key0and record it as key01. Convert these 4-bit binary numbers into decimal numbers. Then take the first 2 bits and the last 2 bits of the 8-bit binary number key0and record it as key02. Convert these 4-bit binary numbers into decimal numbers. Enter the chaotic S-box for nonlinear transformation.The specific operation is indicated by the following formula:

Here, the bin2decc(.) function converts binary numbers into decimal numbers. The key is the value obtained by processing the initial key key0into the chaotic S-box. It is a decimal number.

Step 4 Use the left shift operator. For the decimal number key,the respective loops are shifted leftward by 2 bits and 5 bits. The specific operation is as shown in the following formula:

Step 5 Expand the two-dimensional image matrixP2with a size ofM×Ninto a one-dimensional vectorAi(i=1,2,...,M×N). Then use the following formula to operate:

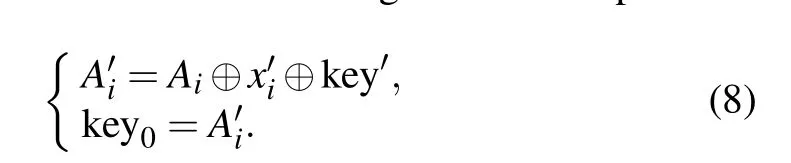
The obtained one-dimensional vectorA＇i(i=1,2,...,M×N)is converted into an imageM×Nand referred to asP3.

Step 6 Enter the keysy0andu4, and substitute the two keys into the logistic chaotic mapping formula. The 1000 iterations eliminate the transient effects. Implement the selectedM×Niterations again. The chaotic sequenceyi(wherei=1,2,...,M×N) is obtained. The chaotic sequenceyiis substituted into the following formula to obtain the processed one-dimensional sequencey＇i:

Fig.2. Flowchart of encryption process.

Step 7 Convert a one-dimensional sequencey＇iinto a twodimensional arrayBwith a size ofM×N. The adjacent-side XOR operation is performed with the encrypted imageP3obtained from the first step of diffusion. The specific description is as follows:

whereEirefers to thei-th element of imageP3.

In summary, the diffusion process for the encrypted imageP2ends. And the diffused image is denoted asC.

Thus,the cipher imageCis obtained.The encryption flow chart of the algorithm is shown in Fig.2.

4. Results of simulation experiment

The simulation experiments in this paper are performed with the software Matlab R2017a. The computer configuration used is a 2.80-GHz CPU,8 GB of memory and Microsoft Windows 10 operating system. In order to verify the effectiveness of the above algorithm,in this paper,Lena,Girl,and House gray digital images with a size of 256×256 are selected as the plain images in the simulation experiment.

Fig.3. Four image encryption/decryption experiment results: (a)Lena,(b)cipher image,(c)decoding image,(d)Girl,(e)cipher image,(f)decoding image,(g)House,(h)cipher image,(i)decoding image,(j)Lena2,(k)cipher image,(l)decoding image.

The encryption and decryption results of Lena,Girl,and House grayscale images are shown in Fig.3. In addition, the chaotic image encryption algorithm is also suitable for the encryption of color images. We only need to decompose the color image into three grayscale images,and then use the algorithm to encrypt the three grayscale images, and finally combine them into a color cipher map.Experiments are performed using a Lena color image, and the results are still shown in Fig.3.

5. Security analysis

5.1. Exhaustive attack analysis

5.1.1. Key space analysis

The key is the core of the entire cryptosystem. Usually,the more the parameters and the larger the key space,the higher the difficulty in deciphering is and the more secure the encryption system. The key space analysis in the algorithm is mainly to prevent possible exhaustive attacks.[19,20]The key of this paper is as follows: the chaotic initial value and control parameters of the logistic chaotic mapping formula in the scrambling and diffusion stage of the plain image; and key0,specifically,a0,b0,x0,y0,u1,u2,u3,u4,and key0. If the computing precision of the computer is 10−14, the key space of the algorithm proposed in this paper is 10126. In Refs.[21,22]proposed was the algorithms with key spaces of 1089and 1098respectively. Therefore, the algorithm proposed in this paper has a larger key space value,and this value meets the security requirements of the key space.

5.1.2. Key sensitivity analysis

In order to test the sensitivity of the key, the initial valuesx0andy0of the chaotic system are increased by 10−14respectively,with the other keys unchanged. The image is decrypted using the correct key and a slightly altered key. The experimental object is a Lena grayscale image.Figure 4 shows the test results. Figure 4(a) shows that using the correct key for decryption,the original image can be correctly decrypted.Figure 4(b) shows the use of the keyx0=x0+10−14for decryption. Figure 4(c)shows the use of the keyy0=y0+10−14for decryption. It can be clearly observed that the two images obtained by being decrypted with the wrong key have no information containing the original image at all. Therefore,the algorithm is very sensitive to encryption keys and has high confidentiality.

Fig.4. Key sensitivity test: (a)decrypt with the correct key,(b)decrypt with wrong key,(c)decrypt with wrong key.

5.2. Statistical attack analysis

5.2.1. Histogram analysis

The histogram statistics of the encryption system is mainly the area that reflects the distribution of image pixel values. After the image is encrypted, the image is not recognized after encryption,and its statistical characteristics will also change accordingly. Generally,the histogram distribution of the plain image is concentrated. After processing by the encryption algorithm, the more uniform the pixel value distribution of the cipher image, the more ideal it is. That is,the more uniform the histogram looks, the better the image is.[23–25]Figure 5 shows the histograms of the plain and cipher images of Lena, Girl, and House, respectively. The experimental results show that the pixel values of the plain image are unevenly distributed,and the pixel values of the cipher image obtained by the algorithm are evenly distributed in the whole pixel space,and the pixel gray value appears in a range of [0, 255]. The probabilities are almost equal, and it can be analyzed that it is difficult for an illegal attacker to use the statistical properties of image pixel values to recover the original image.

Fig.5. Histogram of plain and cipher images: (a)Lena plain histogram,(b)Lena cipher histogram,(c)Girl plain histogram,(d)Girl cipher histogram,(e)House plain histogram,(f)House cipher histogram.

5.2.2. Adjacent pixel correlation analysis

The high correlation of adjacent pixels of an image is an essential feature of digital images. In order to resist the statistical attacks,the correlation of adjacent pixels must be reduced,and the smaller the correlation coefficient,the better the encryption performance is.[26,27]In order to analyze the correlation of adjacent pixels, taking the Girl gray image for example, 104pixel points are randomly selected for correlation analysis. Their correlation coefficients are calculated according to Eqs. (11) and(12).[28]Table 2 shows the correlation coefficients of the three grayscale images in three directions before and after encryption.Figures 6(a), 6(c), and 6(e) show the distribution of adjacent pixel correlations of the plain image of Girl in three directions.Figures 6(b),6(d),and 6(f)show the adjacent pixel correlation distributions of the cipher image of Girl in three directions.

Table 2. Correlation of adjacent pixels.

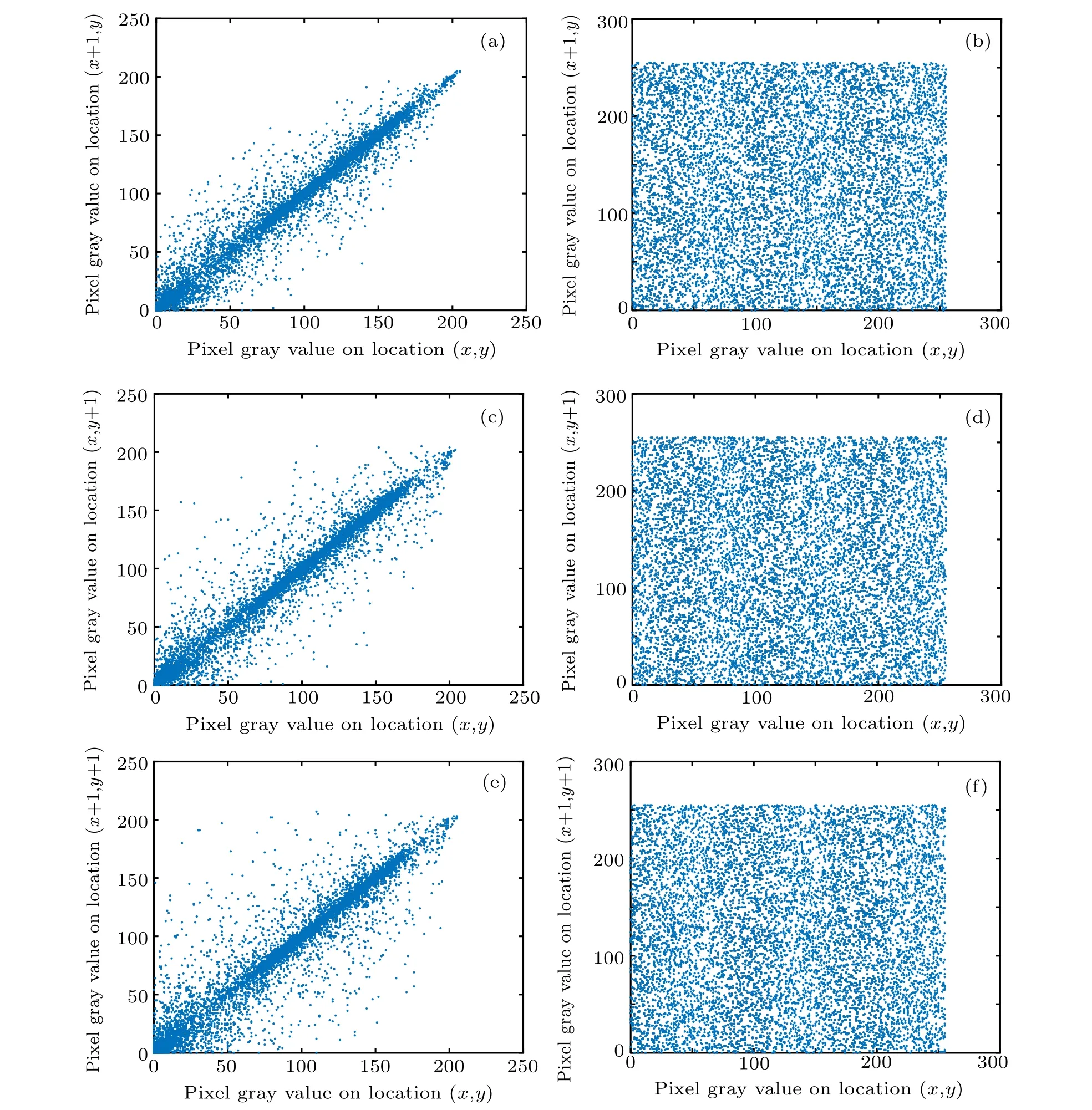
Fig.6. Adjacent pixel correlation between pre-encrypted and encrypted images: (a)horizontal correlation of Girl image,(b)horizontal correlation of cipher,(c)vertical correlation of Girl image,(d)vertical correlation of cipher,(e)diagonal correlation of Girl image,(f)diagonal correlation of cipher.

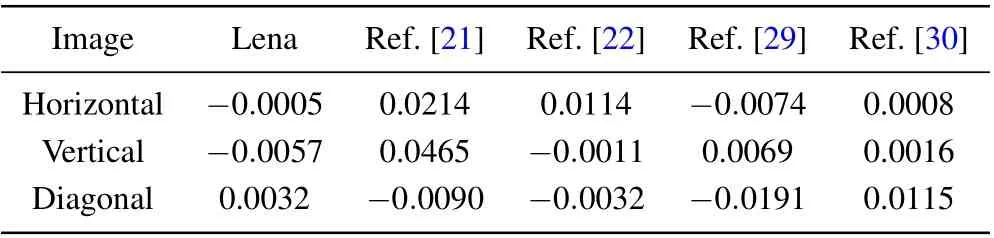
Table 3. Comparisons among correlation coefficients of images.

In addition,in Table 3 the gray-scale image Lena is taken for example,and the experimental results of its adjacent pixel correlation with other algorithms are compared. All experimental results prove that the cipher image correlation is greatly reduced after encryption by the algorithm,which can better resist statistical attacks based on correlation analysis.

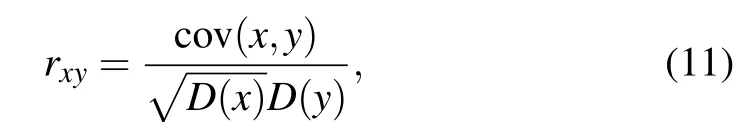
where

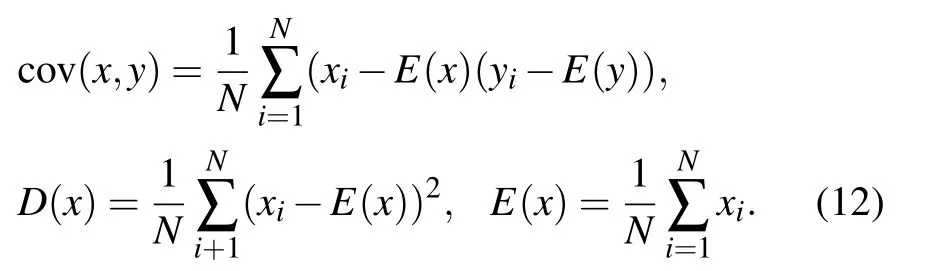
5.2.3. Information entropy

In this subsection the information entropy analysis in security analysis is conducted. It is a measure of the order of information. The closer to a uniform distribution the probability distribution of image pixel values, the larger the information entropy is and the smaller the information entropy. In particular,When there is a probability that the pixel values are equal, the image information is the largest.[31,32]The image information entropy is given by Eq.(13). In Table 4 listed are the information entropy of the plain and cipher maps of the three grayscale images. The experimental results show that the information entropy of each plain image is significantly different from the theoretical value,and all pixel values of the cipher image appear with almost equal probability. In Table 5 the gray-scale image Lena is taken for example to compare the results of the information entropy experiment with those from other algorithms. This proves that the algorithm proposed in this paper is effective.

Table 4. Information entropy of plain images and cipher images.

Table 5. Comparison among results of information entropy.

5.3. Cropping attack analysis

Cropping attack is also a common attack method for an attack to image encryption,launched exerted by an illegal attacker.[33]Therefore, in order to test the resistance of the image encryption algorithm to the cropping attack, proposed in this paper, the cipher graph of the experimental object House in four degrees is cut, then the correct encryption key is input to execute the decryption program, and the decrypted image is observed. Figure 7 shows the experimental results. It can be seen that even if the cipher image is cropped by 1/2 degrees, the plain image can still be recognized after being correctly decrypted. Therefore,the chaotic image encryption algorithm proposed in this paper possesses a certain resistance to cropping attacks.

Fig.7. Recovery after tailoing attacke at different degrees: (a)1/16-degree cropping and decrypting image,(b)1/8-degree cropping and decrypting image,(c)1/4-degree cropping and decrypting image,(d)1/2-degree cropping and decrypting image.

5.4. Noise attack analysis

In a real-time transmission channel,there is often noise that affects the plain image. Noise attacks are also a way to verify the robustness of cryptosystems.[34–36]In order to evaluate the ability of the encryption algorithm to resist noise in this paper,different salt and pepper noise are added to the House cipher image,and the correct key is used for decryption. The experimental results are shown in Fig. 8. The experimental results show that the encryption algorithm of this paper has better resistance to noise attacks.

Fig.8. Cipher image adds different degrees of noise and corresponding decryption maps: (a)cipher and decrypted image with noise intensity of 0.01,(b)cipher and decrypted image with noise intensity of 0.05, (c)cipher and decrypted image with noise intensity of 0.1.

6. Conclusions

In this work, a new image encryption algorithm is proposed. It is based on an improved baker transform and chaos S-box. In the image scrambling phase, the plain image is manipulated primarily using an improved baker transform method. On the other hand, in the image diffusion stage, the chaotic S-box is referenced and the initial key is processed.It also performs XOR operations on image, key, and chaotic sequences. The experimental results and security analysis prove that the digital image encryption algorithm proposed in this paper is effective in resisting multiple attacks; in other words, the image encryption algorithm proposed in this paper is highly secure and excellent encrypted randomness. In addition,in the future direction of work,we can not only starting from the existing encryption methods,improve or propose new encryption methods for chaotic image encryption,but also starting from the chaotic system, improve or propose a more efficient chaotic system, which can be applied to the image encryption algorithms.