A secure image protection algorithm by steganography and encryption using the 2D-TSCC*

Qi Li(李琦) Xingyuan Wang(王兴元) He Wang(王赫) Xiaolin Ye(叶晓林)Shuang Zhou(周双) Suo Gao(高锁) and Yunqing Shi(施云庆)

1School of Information Science and Technology,Dalian Maritime University,Dalian 116026,China

2Guangxi Key Laboratory of Multi-source Information Mining&Security,Guangxi Normal University,Guilin 541004,China

3Dalian Hongwen Middle School,Dalian 116000,China

4School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China

5Department of Electrical and Computer Engineering,New Jersey Institute of Technology,Newark NJ 07102,USA

Keywords: 2D-TSCC,steganography,image encryption,mod diffuse,chaos

1. Introduction

Due to the openness and sharing of the network, the protection of information has become particularly important.Currently, in the era of full coverage of 5G networks, images are one of the important information interaction tools,and privacy-protecting images have gradually become popular research content.[1-3]Preventing the leakage of image information has gradually become a hot research topic.[4-7]Many image protection methods have been proposed,[8-11]such as steganography,zero watermark,image encryption,and so on.[12-17]

Because chaotic systems have the characteristics, such as long-term, sensitive to parameters, sensitive to initial values unpredictable,pseudorandomness,and so on.[18-20]Therefore,the encryption algorithm combined with chaotic systems have received widespread attention.[22,23]Many scholars have proposed encryption algorithms.Ye and Wanget al.,proposed a new Chua’s chaotic system with a higher complexity and the system was simulated by hardware. A nonlinear diffusion encryption algorithm was proposed using the system and Arnold mapping.[24]In order to protect the transmission of medical images, Liu and Kadiret al.used a high-dimensional chaotic system on the Galois field and a new image protection scheme with faster encryption speed was proposed.[25]Hau and Jinetal., proposed a new two-dimensional (2D) chaotic system,which has better dynamic behavior than the past system, and used this system to propose an encryption algorithm with higher encryption efficiency.[26]Parvaz and Zarebnia maked a new system through three common one-dimensional (1D)chaotic systems, and use this system for the protection of binary images and grayscale images.[27]Many algorithms are not resistant to selected plaintext attacks. Zhu and Sun proposed an enhanced algorithm to solve this problem.[28]Ullah and Jamalet al.,used the substitution box and chaotic system in image encryption.[29]Wang and Gao proposed the Boolean network encryption base on chaotic systems,and then used the Boolean network to make the secret key in the chaotic image encryption.[30,31]

Unlike image encryption, steganography not only hides the content of the message,but also hides the communication process itself. Steganography requires a normal digital carrier as a cover to transmit secret information. Steganography have been proposed by many researchers recently. For example, Baluja hides the color image in the same size image.[32]Xie and Changet al., proposed a data hiding scheme which is reversible with a high embedding ability.[33]Ma and Liet al.,proposed the reversible information hiding based on CDM(Code Division Multiplexing).[34]

So far, the image protection algorithms proposed are all single, single encryption algorithm, or single steganography algorithm. In this paper, the two protection algorithms are combined,and the comparative experimental results also show that with the addition of the steganography,the ciphertext image obtained is closer to the theoretical value in various test indicators.Even if the attacker intercepts the ciphertext image,only the carrier image carrying the secret information can be obtained through the decryption algorithm. If attackers want to get a secret image, they must crack the steganography algorithm. This is undoubtedly more difficult than cracking a single steganography algorithm or encryption algorithm.

Many chaotic systems have been proposed.[35-37]The one-dimensional chaotic system is simple in form,the chaotic trajectory of the 1D chaotic system is relatively simple and can be easily destroyed. The destroyed system loses randomness and it is not suitable for image encryption. Chaotic systems with more than two dimensions or spatiotemporal chaotic systems have better chaotic properties, but the efficiency in generating chaotic sequences is low. Therefore,many 2D chaotic systems have been proposed,such as 2D logistic map,[38]2DSLMM,[39]H´enon map,[40]and so on. These systems have some problems, such as the small parameter space in the hyperchaotic state and the uneven distribution of chaotic sequences. This paper proposes a new 2D-TSCC system. The system has a larger parameter space,which allows the system to enter a hyperchaotic state, the chaotic sequence is evenly distributed,and most of the values in the window can be taken.Hence,it is very suitable for image encryption.

In this paper,a new image protection scheme in combination with 2D-TSCC.This solution includes steganography and encryption. Compared with a single steganography or encryption algorithm, the image protection scheme is more secure,because it is very difficult for an attacker to obtain secret information to crack two encryption methods. In the steganography stage,the sequence generated by the 2D-TSCC is used to determine the position of the secret information embedded in the cover image. The sequence generated by the 2D-TSCC is used in the encryption stage for scrambling and diffusion.

2. The 2D tan-sin-cos-coupling map

First, a new chaotic system which is called 2D-TSCC is proposed. Then, the chaotic trajectory, Lyapunov exponents,and NIST test of the system are analyzed. Finally, the 2DTSCC is compared with some other 2D systems.

2.1. Definition of 2D-TSCC

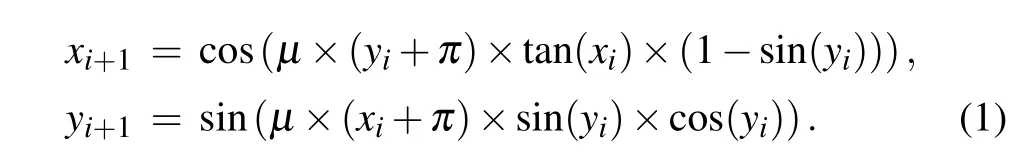
Due to the small parameter range of low-dimensional chaotic systems, the chaotic sequence is not uniformly distributed. Therefore,this paper proposes a 2D chaotic system In Eq.(1),x ∈[−1,1]andy ∈[−1,1]. Whenµ ∈[2.051,10],the system is in a hyperchaotic state,at this time the sequence distribution of the system is uniform,and the periodic behavior is difficult to predict. The chaotic sequence under this parameter is selected for steganography and encryption.

2.2. Chaos trajectory

The chaotic trajectory represents the path of the sequence output. If the trajectory of a chaotic system fills the entire interval,the output of the chaotic system has a better pseudorandomness.

The trajectories of the 2D-TSCC system are shown in Fig.1.The parameters areµ=2.05,µ=4,µ=6,andµ=10.

Fig. 1. Chaos trajectories of the 2D-TSCC, (a) chaos trajectory with µ =2.05, (b) chaos trajectory with µ =4, (c) chaos trajectory with µ =6, (d)chaos trajectory withµ =10.

The chaos trajectories of the 2D-TSCC system is compared with the chaos trajectories of some classic 2D chaotic systems.

(i)2D logistic map is proposed by Wuet al.,[24]

The chaotic trajectory of 2D logistic map(x0=0.5724,y0=0.603, andα=1.18), 2D-SLMM (x0=0.5724,y0=0.603,β=0.9,andε=3),and H´enon map(x0=0.5724,y0=0.603,ξ=1.4,andτ=0.3)are shown in Fig.2.

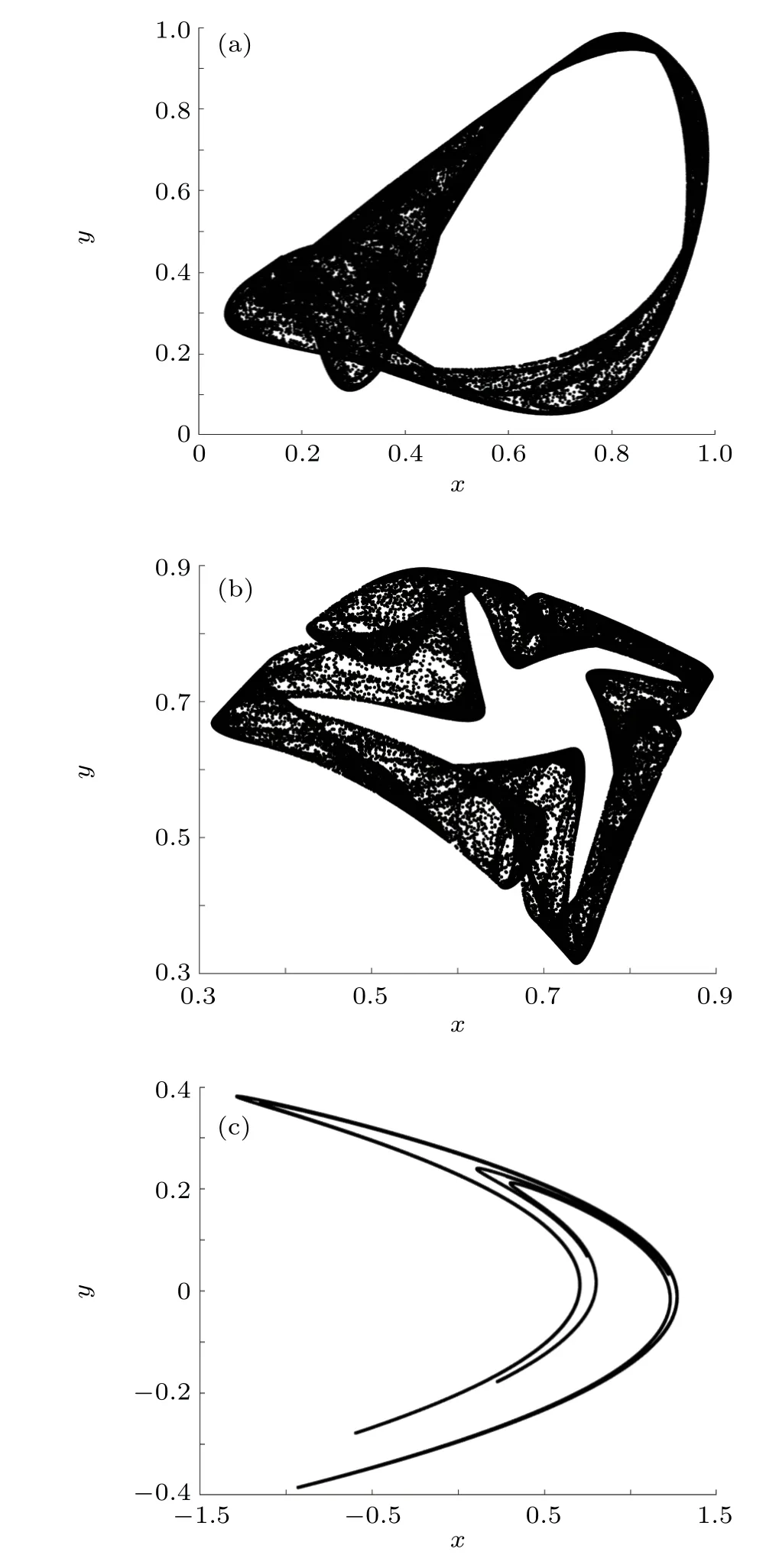
Fig.2. Trajectories of three 2D chaotic maps: (a)2D logistic map, (b) 2DSLMM,and(c)H´enon map.

From Figs.1 and 2,the trajectories of the 2D-TSCC system fills the entire space, while the trajectories of the systems (i), (ii), and (iii) do not fill the entire space. The 2DTSCC system has a wider range of values,which can take all the values in the interval, while the systems (i), (ii), and (iii)can only take part of the values in the interval. Therefore,the value of the 2D-TSCC system is more random,which is more suitable for steganography and image encryption.

2.3. Lyapunov exponents

Lyapunov exponent is an important index that characterizes the dynamic behavior of the system.[41-43]The dynamic system with a positive Lyapunov exponent is chaotic.A high-dimensional chaotic system may have multiple positive Lyapunov exponents. When a dynamic system has two or more positive Lyapunov exponents, the system is hyperchaotic. Hyperchaotic systems have better chaotic characteristics and more complex dynamics.It is defined as follows:[24]

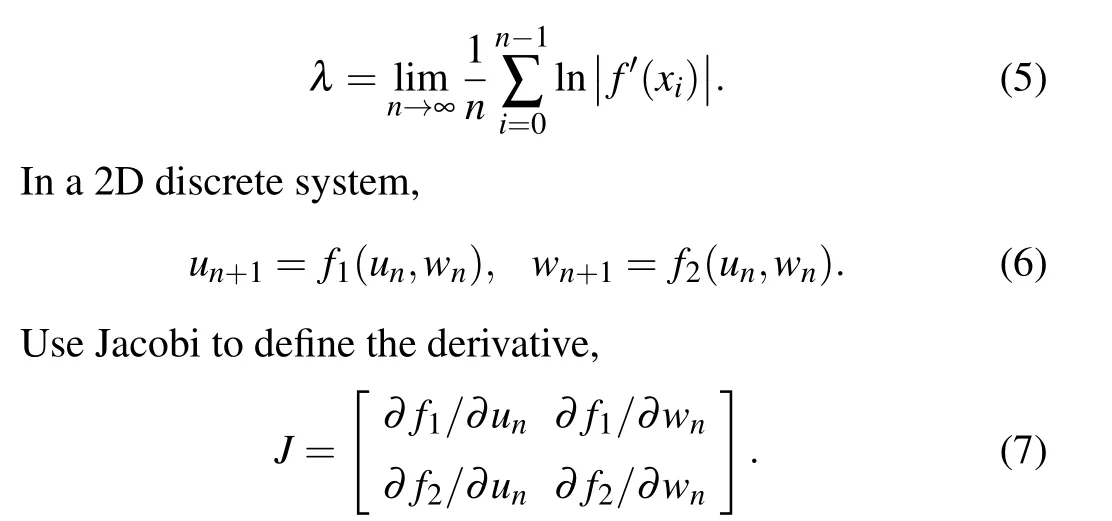
Fig. 3. Lyapunov exponents of 2D-TSCC, (a) Lyapunov exponents withµ ∈[0,10], (b) Lyapunov exponents with µ ∈[1.2,2.8], and (c) Lyapunov exponents withµ ∈[3.4,4.3].

It can be seen from Fig. 3, whenµ ∈(1.33,1.425) andµ ∈(1.435,1.53), the system is in a chaotic state. Whenµ ∈(1.56,1.59),the system switches between chaos and hyperchaos. Whenµ ∈(2.051,10], the system is in a hyperchaotic state. This paper selects the parameters in a hyperchaotic state, and generates a chaotic sequence for steganography and encryption.

The Lyapunov exponents of systems(i),(ii)(ε=3),and(iii)(τ=0.3)are shown in Fig.4.

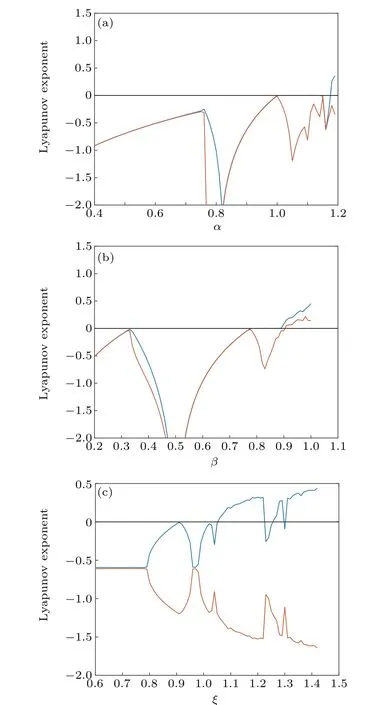
Fig.4. Lyapunov exponents:(a)Lyapunov exponents of 2D logistic map,(b)Lyapunovs exponents of 2D-SLMM,and(c)Lyapunov exponents of H´enon map.

Comparing the Lyapunov exponent of systems (i), (ii),and (iii), the 2D-TSCC has a wider range of parameters in a hyperchaotic state, so the 2D-TSCC system is more suitable for steganography and image encryption.

2.4. NIST test

In this section,the randomness of the sequence generated by the chaotic system is tested by NIST,and the test results are shown in Table 1.

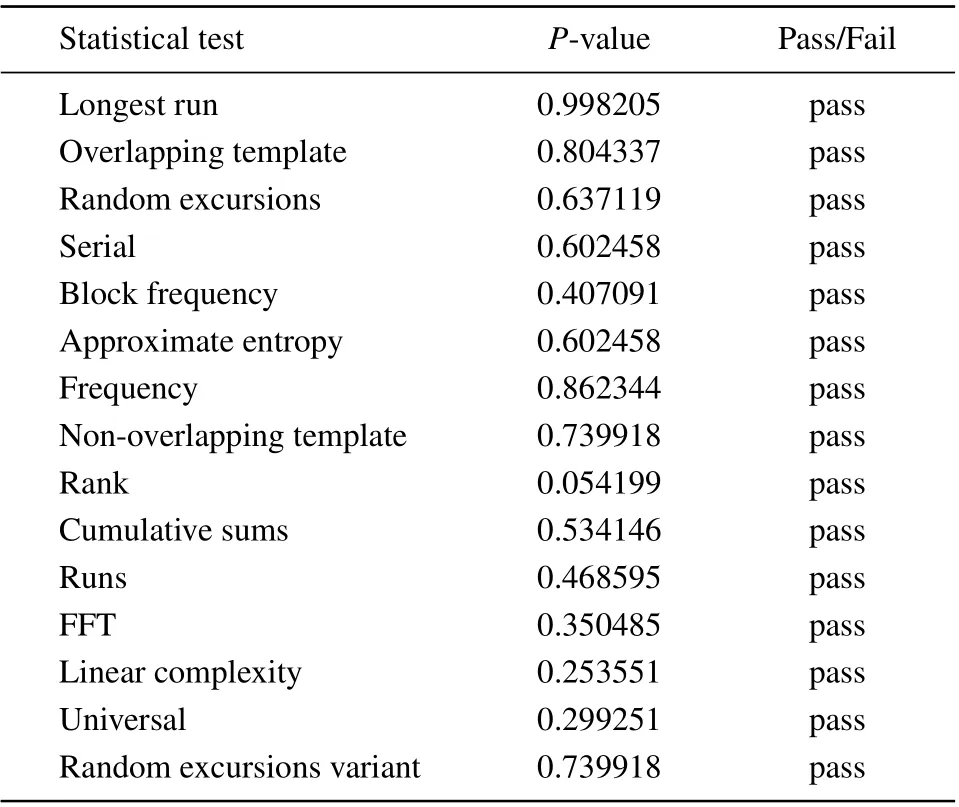
Table 1. NIST test of the chaotic sequence.

The chaotic sequence generated in this paper has passed 15 tests,so it can show that the sequence generated by the 2DTSCC has good randomness.

3. Steganography and encryption algorithm

This section proposes a safe method of protecting images,which includes steganography and encryption. First,an image that needs to be protected is steganographically written in a carrier image, then combined with the 2D-TSCC, the carrier image embedded in the secret image is encrypted,and the ciphertext is obtained,thereby playing the role of double protection of the image.

3.1. Steganography

Steganography is a way of hiding information. Steganography focuses more on making people unable to perceive the existence of secret image. The plaintext is hidden in the cover image by substitution. Suppose the secret image isHS×Tand the cover image isPM×N. The steganography algorithm is as follows.

Step 1 Convert the cover image to a binary image, and each pixel value includes 8-bit values. Each bit can form an image,

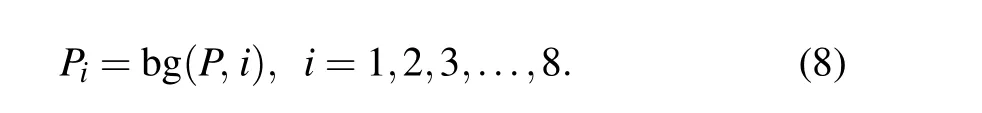
In Eq. (8), bg(x,y) represents the extraction of they-th from the binary numberx. Two examples are given as

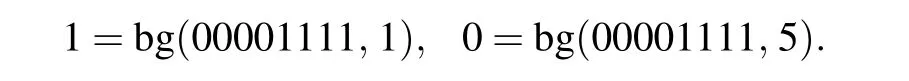
Take the Lena as an example. According to the above steps,8 images can be obtained in Fig.5.

The 1 in the first bit only represents 1 (20), but in the eighth bit, it represents 128 (27). Therefore, use the following formula to describe the amount of information contained in each bit:[44]It can be seen from Table 2 that the 1st bit,the 2nd bit,and the 3rd bit contain the least amount of information, so the secret image is hidden in these three bits of the cover image.

Table 2. Information of different bits.

Fig.5. Image at each bit, (a)image of the 1st-bit, (b)image of the 2nd-bit,(c)image of the 3rd-bit,(d)image of the 4th-bit,(e)image of the 5th-bit,(f)image of the 6th-bit,(g)image of the 7th-bit,and(h)image of the 8th-bit.

Step 2 Convert the secret image to a binary,a key stream is generated by the 2D-TSCC system,and determine the position of the secret image inserted into the cover image according to this key stream. Each pixel value of the cover image can carry one bit of the secret image.The cover image carrying the secret image is obtained.

According to the rules, the relationship of the secret imageHU×Tthat the cover imagePM×Ncan carry is

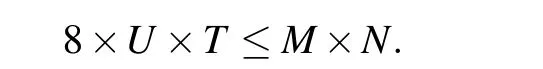
3.2. Steganography and encryption base on chaos

The secret image isHU×Tand the cover image isPM×N,the carrier image containing the secret information isPH. The algorithm is described as follows.

Start Input the cover imagePM×Nand the secret imageHU×T.

Step 1 The secret keyhis generated from the cover image through SHA512,

Step 6 Convert the secret image to a binary image, the size of the bit stream contained in secret image is 8×U×T.Take the first 8×U×Telements of the cover image and convert them to bits. Then the secret imageHis steganographically written in the cover imagePand the new cover imagePHis obtained as

Step 10 Find the point with the same number inA3, and recordA4as

Step 11 Scrambling the cover imagePHaccording toA4,the scrambling method is

In Eq.(19),CS(a,b)is the displacement function,an example ofCS(a,b):

For a better understanding, the following shows the scrambling process with an example,as shown in Fig.6.

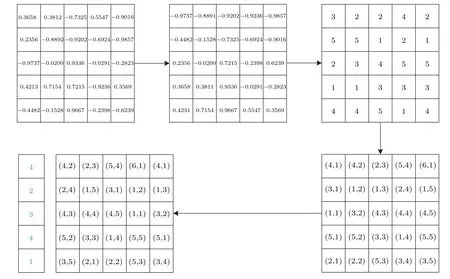
Fig.6. An example of scrambling.

Step 12x0=d3,y0=d4,andµare brought into the 2DTSCC system to get the chaotic sequencesXandY,

Step 13 Process the scrambling matrixSto get the ciphertextC:

The reverse operation of this process is

End Output ciphertextC.

4. Performance analysis

Some experimental results of the algorithm are given in this section. Some tests are performed on the experimental results to verify safety,including statistical tests and robustness analysis.

4.1. Experimental results

Fig. 7. Experimental results: (a) secret image, (b) cover image, (c) cover image carrying secret image,(d)scrambling of image(c),(e)encrypted image of panel(d), (f) decryption of cover image containing secret image, (g)decrypted cover image,and(h)decrypted secret image.

4.2. Key space analysis and key sensitivity analysis

The secret key in this article is generated by SHA512,as shown in Step 2 of Subsection 3.2. Select the first 384 bits of SHA512. The key space size is:

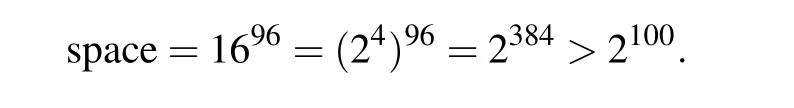
When the key space is greater than 2100, it is considered that this algorithm can resist brute force attacks. The key space of this article is 2384, so an attacker cannot crack the algorithm by brute force attacks.

Fig. 8. Key sensitivity analysis: (a) restore through the correct key, (b) restore through the key of b1+10−15,(c)restore through the key of b2+10−15,(d) restore through the key of b3+10−15, (e) restore through the key of b4+10−15,(f)restore through the key of b5+10−15,and(g)restore through the key of b6+10−15.

Experiments show that the algorithm proposed in this paper is sensitive to the secret key, and the decryption key is unique. The algorithm can only get the plaintext information through the secret key provided by the sender,so the algorithm is safe.

4.3. Histogram analysis

The histogram analysis is an indicator to describe the distribution ofpixelvalues,whichisto countthe frequency of the same pixelvalue inthe image.[45]Usually thepixel value distribution of the plaintext is not uniform, but after a secure encryption algorithm, the number of times the same pixel value of the ciphertext appears is almost equal. Uneven histograms can cause information leakage, and attackers can crack the algorithm based on statistical analysis. The secret image Mangray 128×128 is hidden in the cover image Lenagray 512×512,the histogram analysis of Man gray,Lena, Lena-Man, and the ciphertext of Lena-Man are shown in Fig.9.

Fig.9. Histogram analysis: (a)secret image of Man,(b)histograms of Man,(c)cover image of Lena,(d)histograms of Lena,(e)cover image carrying secret image of Lena-Man,(f)histograms of Lena-Man,(g)ciphertext of Lena-Man,and(h)histograms of ciphertext.

The distribution of the histogram of the cover image carrying secret image is not uniform,but after the encryption algorithm in this article,the distribution of the histogram of the ciphertext is uniform. A attacker cannot infer the information of the cover image from the ciphertext,so the algorithm has a better ability to resist statistical attacks.

4.4. Adjacent pixel correlation

The adjacent pixel correlation is another indicator of resistance statistics. The adjacent pixel correlation analyzes the adjacent pixel correlation(horizontal,vertical,diagonal).Normally, the adjacent pixel correlation of the plaintext is very large. After a secure encryption algorithm,the adjacent pixel correlation of the ciphertext is very small. A attacker cannot infer the distribution of the plaintext through the ciphertext. The calculation formula of adjacent pixel correlation is described as follows:[46]

where,

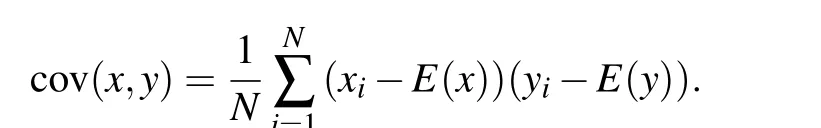
This article analyzes the adjacent pixel correlation (horizontal, vertical, diagonal) of this algorithm from two angles. (I)Test the ciphertext obtained by the encryption algorithm on the carrier image,and test the correlation between adjacent pixels of the ciphertext. (II) After the test carrier image is embedded with the secret information Man,a new carrier cover-Man is obtained, and the new carrier is encrypted , Test the correlation between adjacent pixels of the ciphertext. Figure 10 shows different cover images.Table 3 shows the adjacent pixel correlation.

It can be seen from Table 3 that the correlation of the cover image is large, but after the encryption algorithm, the correlation of the ciphertext is small. The ciphertext of the cover image containing secret image and the ciphertext of the cover image not containing secret image have little fluctuation in correlation. Therefore, it can be shown that the algorithm has a good ability to resist statistical attacks.

Table 3. Adjacent pixel correlation.

Fig.10. Cover images.

4.5. Information entropy

Information entropy is an important indicator for detecting the distribution of image pixel values, it is calculated as follows:

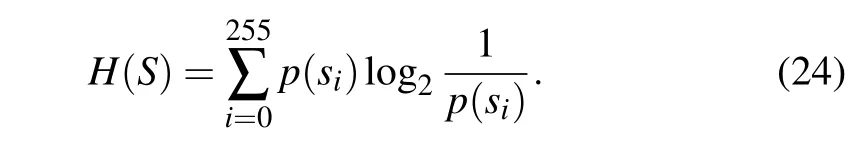
The value of information entropy is closer to 8,indicating that the information contained in the image is confusing, and the attacker cannot find useful information on the image. On the contrary,the value is far away from 8,indicating that the possibility of information leakage is high,and the attacker can find the key information cracking the algorithm.

The information entropy of the algorithm is analyzed from two perspectives. One is to test the ciphertext information entropy of the cover images in Fig. 10, and the other is to test the ciphertext information entropy of the cover images who is embedded with the secret image of Man.Table 4 shows the information entropy of the two ciphertexts.

The following conclusions can be drawn from Table 4.The information entropy of the ciphertext obtained by the algorithm is close to 8. When only the encryption algorithm is used, the maximum value of the algorithm is 7.99943, the minimum value is 7.999925,and the average value is 7.99932.When the secret image is embedded in the carrier image to obtain the ciphertext image. The maximum value is 7.99941,the minimum value is 7.99920,and the average value is 7.99932.The ciphertext of the cover image containing secret image and the ciphertext of the cover image not containing secret image have little fluctuation in information entropy. Therefore,it can be explained that the attacker cannot obtain the key information to estimate the distribution of the plaintext pixel value,so the algorithm is security.

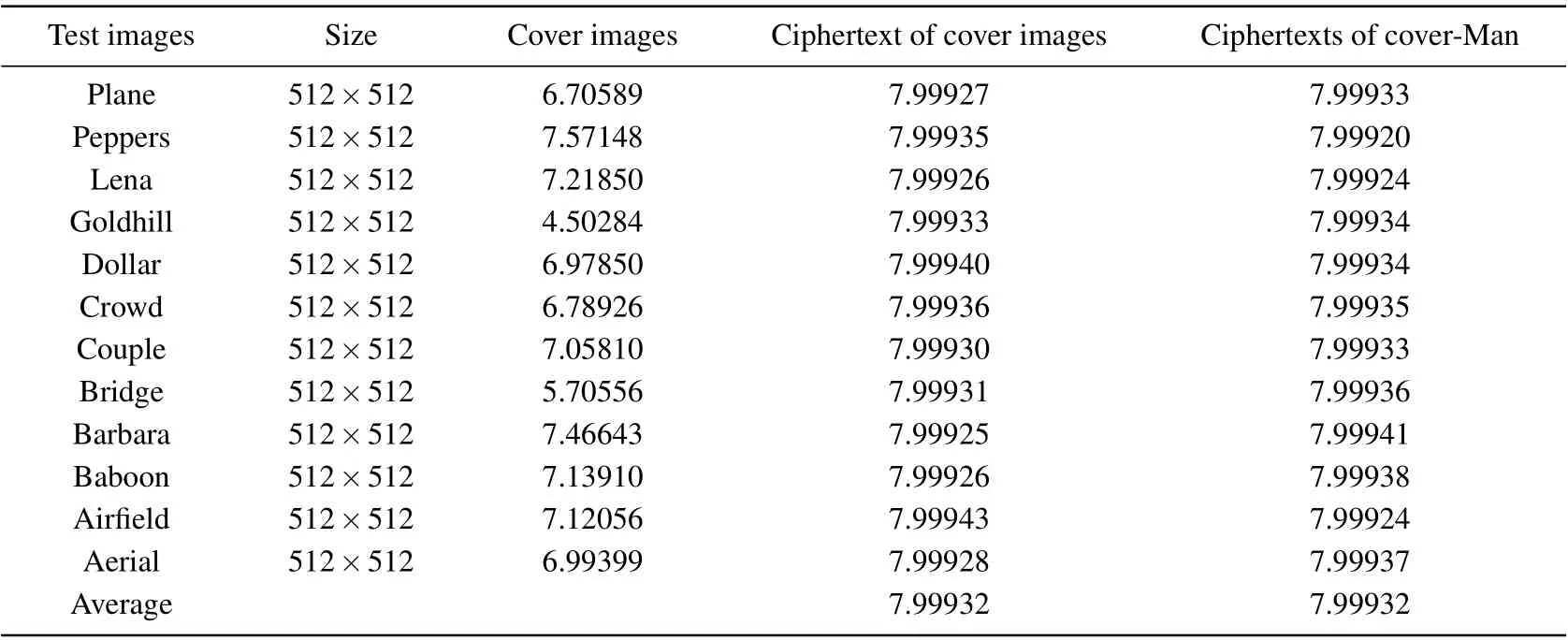
Table 4. Information entropy.

4.6. Differential attack

The number of pixels changing rate(NPCR)and unified averaged changed intensity (UACI) are important indicators of the differential attacks. A attacker observes the difference between the two ciphertexts by making a small change to the plaintext. A secure algorithm,even if a small change is made to the plaintext, the ciphertexts are different. The NPCR and UACI are defined as In Eq.(25),D(i,j)=0 ifC1(i,j)=C2(i,j),andD(i,j)=1 ifC1(i,j)̸=C2(i,j).

The NPCR and UACI are analyzed from two perspectives. One is the ciphertext of the cover image and ciphertext of the cover image change one bit, and the other is the ciphertext of the cover image containing the secret image and the ciphertext of the cover image containing the secret image change one bit. Each image randomly selects 50 groups of points for testing,and the average value is shown in Table 5.

When only the encryption algorithm is used, the maximum values are 99.6368 and 33.5284,the minimum values are 99.5789 and 33.4185,and the average values are 99.6074 and 33.4704.When the secret image is embedded in the carrier image to obtain the ciphertext image. The maximum values are 99.6151 and 33.5561, the minimums value are 99.5853 and 33.3931,and the average values are 99.6024 and 33.4722.

The experimental data in Table 5 show that the NPCR and UACI are very close to the theoretical values,so it is possible to show that the algorithm proposed in this paper has the ability to resist the differential attack.

Table 5. NPCR and UACI.

4.7. Robustness analysis

In general, information will suffer some interferences during transmissions, such as loss of some information and noise attacks. Even if a secure algorithm is subjected to these attacks, it can still get some information of plaintext through decryption algorithm. In this subsection,we perform different levels of cropping attacks and noise attacks on the ciphertext.Cove image and secret image are obtained through the decryption algorithm which are shown in Figs.11-14.

Fig. 11. Decryption results after 1/8 cropping attacks: (a) 1/8 block attack,(b)decrypted of cover image,and(c)decrypted of secret image.

Fig.12. Decryption results after 1/16 cropping attacks:(a)1/16 block attack,(b)decrypted of cover image,and(c)decrypted of Secret image.

Fig.13. Decryption results after 0.1 salt&Pepper noise: (a)0.1 salt&Pepper noise,(b)decrypted of cover image,and(c)decrypted of secret image.

Fig. 14. Decryption results after 0.01 salt & Pepper noise: (a) 0.01 salt &Pepper noise, (b)decrypted of cover image, and(c)decrypted of secret image.

The experimental results show that even if the ciphertext has been attacked,partial information can still be obtained by decryption. Therefore,the algorithm has better robustness.

4.8. NIST test

This section uses the NIST test to test the randomness of the ciphertexts,and the test results are shown in the following Table 6.

Table 6. NIST test of the ciphertexts.

The test results show that the ciphertext obtained by the algorithm has good randomness.

4.9. Comparing with other algorithms

The proposed algorithm is compared with some classic encryption algorithms(Refs.[7,47-50]),including the information entropy,the adjacent pixel correlation,the NPCR,and UACI,the results are shown in Table 7.

Table 7. Compare with other algorithms.

5. Conclusion

A safe image protection scheme is proposed in this paper.The highlight of this paper are as follows:

(I)This paper proposes a new 2D chaotic system,i.e.,2DTSCC.Compared with other 2D chaotic systems,this system has a larger parameter space and the chaotic trajectory spreads over the entire window, so it is more suitable for image encryption and image steganography.

(II)Combined with 2D-TSCC,a dual protection scheme for images is proposed. The program includes image steganography and image encryption. The design of this algorithm can ensure the security of the image during transmission.

(III) Compared with other algorithms, including information entropy,NPCR,UACI,adjacent pixel correlation,and other indicators,this algorithm has better security.

The proposed algorithm can be applied to the protection of trademarks and some design drawings. In order to prevent these commercially valuable information from being stolen during transmission. In the transmission process, the algorithm proposed in this paper is used for protection to achieve the role of information protection.

In this paper, the algorithm is a new attempt to combine steganography and encryption. Although the embedding ability of the algorithm is low,the experimental results show that the ciphertext is more secure. In future work, we will design algorithms that combine steganography and encryption with higher embedding capabilities.