基于无限元方法的直升机外部噪声仿真分析

曹荣富，吴林波，吴裕平

（中国直升机设计研究所，景德镇333001）

在直升机广泛应用的今天，其噪声问题日益突出。民用直升机由于其经常在人口稠密的城区作业，噪声污染严重，而军用直升机也因其隐身需求，对机外噪声不断提出新的要求。《航空器型号和适航合格审定噪声规定》[1]对民用直升机适航取证过程中的噪声水平提出了明确要求。随着社会发展，其限制要求也越来越高。直升机机外噪声主要由旋翼和尾桨等产生的中低频噪声以及发动机等产生的中高频噪声组成。机外噪声评估主要采用声学类比法，即将计算流体力学和计算气动声学相结合进行远场噪声求解。以计算流体力学（Compu‑tational fluid dynamics,CFD）计算得到的流场结果作为声学评估的输入，再采用各种声学算法计算流体产生的噪声源以及声音的传播特性。目前，国内已开展了较多关于孤立旋翼和尾桨的气动噪声研究,韩忠华[2]、段广战[3]、王阳等[4]学者先后在各自的领域将CFD方法用于孤立旋翼的气动噪声仿真分析，仲唯贵[5]则基于神经网络建立了直升机适航噪声预估方法，张勇勇等[6]对轻型民用直升机的适航审定状态气动噪声仿真进行了探索，总体上对直升机实际机外噪声研究较少。直升机机外噪声的主要影响因素、影响程度和影响机理不甚明确。

直升机流场仿真是采用声学类比法进行气动噪声仿真的基础，但由于直升机存在旋翼/尾桨/机身等部件的耦合干扰，其气动环境极其复杂，国内已有较多的学者开展了直升机非定常气动环境的仿真分析研究，樊枫等[7]采用CFD方法对直升机旋翼/尾桨的非定常气动干扰进行了计算，谭剑锋等[8]基于自由尾迹的方法开展了旋翼/机身非定常气动干扰数值分析，叶舟等[9]对直升机旋翼/尾桨/垂尾气动干扰进行了研究。常规的孤立旋翼/尾桨远场噪声主要采用FW‑H方程进行评估，直接选取流场中物面或者空间虚拟面进行噪声分析，该方法适用于自由场分析，难以考虑机身声散射和大气声衰减等物理特性,同时也无法给出机身附近的声场分布。杨瑞梁[10]、吴国荣[11]、王超等[12]学者通过研究发现声学无限元法可以有效地解决声波在介质中的传播和衰减问题。基于该特点，无限元法已在列车[13]和船舶[14]等行业的声学仿真和设计中得到应用。

直升机飞行过程中，作为直升机主要远场噪声源的旋翼和尾桨气动噪声经过机身声散射和大气声衰减后向远场辐射。因此，只要能够成功地将考虑了旋翼和尾桨复杂运动的直升机流场与考虑声波在介质中传播和衰减的声学有限元方法相结合，就能有效地用于直升机远场噪声预测，同时给出直升机机身附近的声场分布，为直升机舱内噪声评估与设计提供气动噪声源。

本文引入声学有限元/无限元模型，考虑固体边界的声散射效应和大气传播中的声衰减特性，建立了耦合旋翼/尾桨/机身等部件的直升机全机噪声预测方法。依托AC311A直升机平台，依据噪声适航规范要求，开展该型机通场飞越噪声的计算和分析。进行同状态直升机飞行噪声的外场试验，通过数值计算和试验结果的误差分析，为后续机外噪声评估算法和仿真模型的进一步优化提供基础。

1 声学无限元算法及仿真模型

1.1 无限元法

声学无限元算法本质上是以近声场采用有限元算法，辐射声场采用无限元的方式将有限的几何空间进行无限延展。将CFD计算得到的流场结果用有限元算法来模拟近声场，用基于无反射边界条件的无限元来模拟辐射声场。以有限元模型构建的人工边界作为无限元的基单元，以基单元和相应的无限几何空间构成无限元，从而实现有限元与无限元的耦合。

以椭球坐标系（r，θ，Φ）的无限元法为例，r表示椭球面上任一点到坐标原点的距离，0≤θ≤π，0≤Φ≤2π，对应的笛卡尔坐标方程为

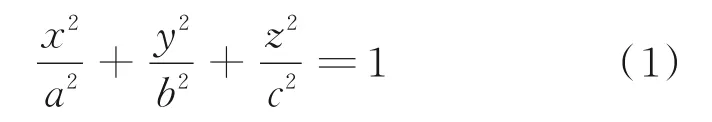
式中：a、b、c分别表示椭球的长轴、中轴和短轴半径；将无限元网格沿r、θ、Φ三个方向进行离散为一系列面元，声场中的声压表示为

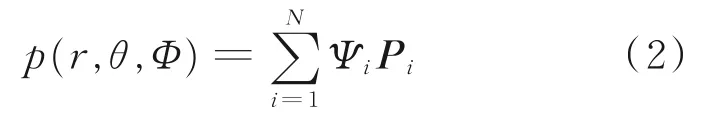
式中：Ψi为无限元的形函数，Pi为边界声压向量。

1.2 无限元模型

由于直升机旋翼桨叶具有挥舞、摆振和周期变距等复杂运动，声学网格难以跟随旋翼/尾桨桨叶相位进行实时变化。常规的孤立旋翼气动噪声仿真分析过程中，常采用基于空间虚拟面的FW‑Hpds方程计算旋翼的远场总噪声，该方法不用直接捕捉旋翼的实时运动轨迹以及旋翼附近的流场信息。借鉴该方法的思想，如图1所示，考虑旋翼和尾桨周期运动形成的包络，在包络外引入封闭曲面代替旋翼和尾桨形成的声源信息；面声源外层为包含了直升机机身的体声源区域，采用有限元来仿真机身附近的声场。在整个有限元的外边界包裹的球形面作为无限元面，声波从无限元面往远场辐射。在此假设直升机机身对声波无吸收，即声波能在机身表面100%反射。声场计算采用频域分析方法，将CFD的流场结果加载到声学网格上，作为气动噪声源，再将时域结果通过傅里叶变换转化为频域结果，根据声波波动方程并引入大气声衰减和机身声散射等声学特性进行声学辐射场计算。

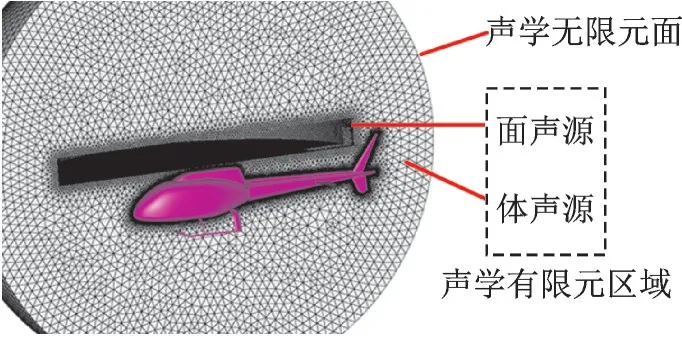
图1 声学计算模型Fig.1 Acoustic computational model

1.3 声学控制方程

本文噪声计算采用声学仿真软件Actran，其采用的无限元法是基于Lighthill声类比法结合格林函数进行的声场仿真，其控制方程为

式中：ρ为当地密度，ρ0为环境密度，（xi，xj）为当地坐标，（vi，vj）为当地速度矢量的分量，Ω为有限元单元体积分域，Γ为有限元单元的表面，ni为Γ的表面法向矢量分量，Tij=ρ0vi vj，∑ij=vi vj+(pp0)δij-τij。式（3）等号右边第1项为体积分，第2项为面积分，分别与图1声学计算模型中的体声源和面声源相对应。

2 UH‑1验证算例

本文中采用UH‑1旋翼悬停算例为例，进行评估分析，并与文献[15]所提供的数据进行对比。UH‑1旋翼基本参数如表1所示。

表1 UH‑1旋翼基本参数Table 1 Basic parameters of UH‑1 rotor

对该旋翼采用结构化运动嵌套网格系统进行网格划分，以RANS方程为控制方程，进行旋翼流场计算，并将流场计算结果作为噪声计算输入数据，进行噪声计算。对于UH‑1旋翼，文献[15]中监测点频谱数据计算总声压级为107.7 dB，仿真分析的总声压级为106.9 dB。图2给出了本文与文献[15]在监测点处声压级对比结果。从图2中可以看出，监测点处频域结果吻合较好，说明本文建立的仿真分析方法及分析模型可以用来评估直升机噪声水平。

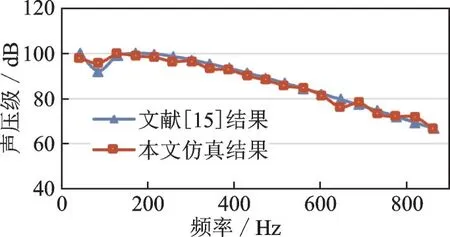
图2 监测点声压级Fig.2 Comparison of sound pressure levels at monitoring points

3 AC311A直升机机外噪声评估

3.1 全机流场计算

3.1.1 流场计算方法

全机流场计算以RANS方程为控制方程。在求解过程中，空间离散格式采用MUSCL+Roe的二阶逆风格式，时间推进则使用双时间法和隐式LU‑SGS格式，湍流模型采用k‑ω两方程模型。

3.1.2 流场计算模型及输入参数

为模拟直升机飞行过程中旋翼的旋转、挥舞及周期变距等运动，基于运动嵌套的混合网格系统对AC311A直升机旋翼/尾桨/机身以及主桨毂整流罩等部件进行了仿真建模，其中旋翼和尾桨采用结构化网格，背景网格为包含了机身和主桨毂整流罩的非结构化网格，流场网格示意图如图3所示，整机流场计算模拟的网格量为5 200万个。

图3 整机流场计算网格Fig.3 Computational fluid grids of full fuselage

为对水平飞越状态下整机流场进行仿真，对直升机全机进行六力素配平[16]，得到机身姿态角和旋翼/尾桨的运动规律，作为流场仿真的参数输入，主要输入参数见表2。

表2 流场计算主要输入参数Table 2 Main input parameters of flow field calculation

3.1.3 流场计算结果

采用本文的流场计算模型和计算状态，进行了AC311A直升机水平飞越状态的流场评估，最终全机升力为22 800 N，该升力结果与AC311A的最大起飞重量一致。气动噪声是压力脉动在空气中的传播，图4给出了尾桨分别与主桨、平尾以及主桨尾涡干扰导致的压力脉动，从图中可以看出，主/尾桨在特定的相位下会产生强烈的气动干扰，与旋翼尾涡之间也存在干扰，但干扰相对较弱，同时，由于尾桨与平尾较近，尾桨气流会击打在平尾上。

图4 主/尾桨以及平尾之间气动干扰引起的压力脉动Fig.4 Pressure fluctuation caused by aerodynamic interference of main/tail rotor and horizontal tail

3.2 机外噪声计算

3.2.1 远场辐射模型

机外噪声计算分为近场计算模型和远场辐射模型，其中近场计算采用图1中给出的声学模型，网格量为500万个。远场辐射计算时，考虑到直升机实际飞行过程中，常采用地面固定测量站的方式测量声压时间历程，该方式在仿真分析中比较难以实施。为此在直升机下方150 m，沿直升机飞行方向前后各500 m，每隔6.19 m布置声学监测点，捕捉直升机声压级随距离和方位变化。远场辐射模型示意图如图5所示。图5中尺寸为示意，不成比例。根据各监测点与直升机的相对位置，换算成直升机飞越过程中，中心监测点（即测量试验过程中的地面麦克风，在下文中两者统一成为中心监测点）的声压级时间历程，再依据《航空器型号和适航合格审定噪声规定》[1]的要求，进行声暴露级求解。

图5 声场计算示意图Fig.5 Schematic diagram of sound field computation

3.2.2 声学计算结果

直升机旋翼和尾桨除了会引起强烈的远场辐射噪声外，同时也是舱内噪声的重要组成部分。图6给出了旋翼桨盘及机身附近声压级分布云图，该声压级能够作为声载荷用于舱内噪声评估。图6中显示，相较于机身，旋翼为直升机的主要噪声源，前行侧声压强度明显强于后行侧，主要是由于前行侧上桨叶实际来流马赫数较大；在机身的桨毂中心及塔座附近噪声最为强烈，机头和垂尾附近较为强烈，尾梁附近和机腹下方最弱。结合图4气动干扰形成的压力脉动分析，旋翼尾涡与桨毂整流罩、尾桨和垂尾之间形成了强烈的气动干扰。

为直观显示直升机声学辐射特性，图7给出了半径为3R的声压级球状分布云图。从图7中可以看出，在直升机前进方向下方30°左右的方位噪声最为强烈为124 dB，直升机的后下方噪声次之，其声压级为116 d B，直升机两侧噪声最弱，其中旋翼前行侧略强于后行侧，其声压级分别约为105 d B和100 dB。

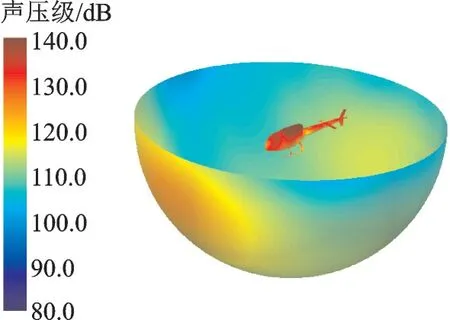
图7 声压级球状分布云图Fig.7 Spherical distribution nephogram of sound pressure level

4 飞行试验验证

4.1 飞行试验

民用直升机在进行适航取证过程中，必须评定其噪声水平。对于最大审定起飞质量不大于3 175 kg的直升机可以仅采用水平飞越状态下的声暴露级来表明直升机的噪声符合性。为此，2015年10月27日在景德镇罗家机场，进行了AC311A直升机水平飞越状态的机外噪声测量飞行试验[17]。该飞行试验是在地面离地高度1.2 m处布置测量麦克风，用以测量直升机飞越经过麦克风期间的声压时间历程。试验机的质量为2 250 kg，正常重心，飞行速度为真空速223 km/h，飞行高度为150 m。图8给出了测试现场的图像，图中铁框用于捕捉直升机水平飞越经过地面测量站上方时的航迹偏差。

图8 AC311A噪声测量飞行试验Fig.8 AC311A noise measurement flight test

直升机机外噪声的适航审定状态比较简单，但为确保试验结果的可靠性，适航规章对试验场地、气象条件、飞参稳定性以及飞行航迹等均有严格的要求。经过对10次飞越过程中（顺风和逆风各5次）的气象条件、飞行速度、旋翼转速、发动机功率、飞行航迹偏差以及地面测量站噪声信号等数据的有效性判定，从中选取了6次飞越结果（顺风和逆风各3次）用于直升机声暴露级（Sound exposure level，SEL）评定，SEL的评定公式为

式中：T0为1 s的基准求和时间；（t2-t1）为求和时间间隔；LA(t)为随时间变化的A计权声级；n为每秒采样数。

4.2 仿真结果对比分析

由于飞行试验仅在地面布设了1组麦克风，无法通过该飞行试验反应直升机的实际辐射特性，本文采用图5的声场计算模型得到的A声级时间历程与飞行试验的A声级时间历程进行仿真结果验证。图9给出了10 d B降区间的仿真分析结果与飞行试验结果的A声级偏差以及偏差量相较于飞行试验结果的百分比。图9显示，在10 dB降区间内偏差较小，最大偏差量为-2.9 d B，偏差百分比为3.8%。将时间历程结果按适航规定进行声暴露级计算，考虑到机外噪声中存在的由旋翼/尾桨等产生的中低频旋转噪声和涡流噪声以及发动机等产生的高频噪声[18]，而本文建立的方法主要适用于中低频噪声评估，对仿真结果进行高频噪声修正，得到SEL仿真分析结果比飞行试验结果低1.13 d B。

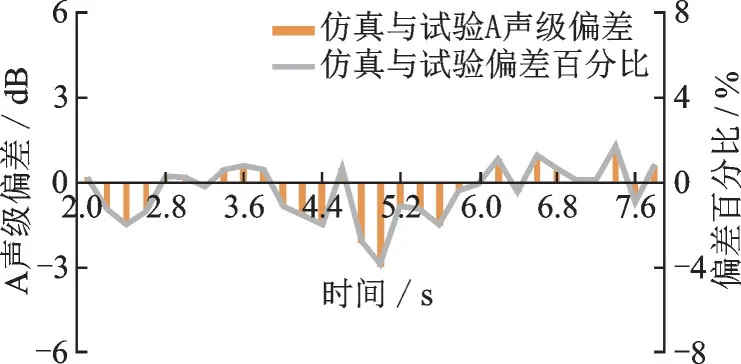
图9 飞越过程10 d B降区间Fig.9 10 dB descending range during over flight

本文基于无限元法建立的直升机机外噪声计算方法和模型，能够有效地进行直升机机外噪声评估分析，其结果能够满足工程应用需求，但仿真结果与试验结果仍有一定误差，对此主要有如下可能因素：

（1）配平数据与实际飞行的差别。飞行试验无法获得直升机旋翼/尾桨的运动规律，虽然进行了直升机六力素配平，但配平得到的直升机姿态、旋翼/尾桨的运动规律等不可避免地会与实际状态下存在差距。

（2）仿真模型与实际测量的差别。实际测量过程中地面麦克风是实时测量直升机飞越过程中的时间历程，仿真算法则是在直升机下方布设一系列监测点，通过对空间的离散来代替时间的离散，根据流场和声场多个周期仿真结果得到的等效声压级。

5 结 论

本文建立了耦合CFD/CAA的直升机机外噪声预测方法，以AC311A直升机为例，进行了水平飞越状态下飞行噪声的仿真分析，并与飞行试验结果对比验证，获得结论如下：

（1）仿真分析结果与飞行试验结果吻合较好，本文基于无限元方法建立远场噪声计算方法及模型，可以用于工程中直升机机外噪声仿真分析工作。

（2）本文计算得到的机身附近声压级结果，可以作为声载荷用于舱内噪声分析。

（3）直升机机身表面噪声分布不均匀，桨毂中心及塔座附近噪声最为强烈，机头和垂尾附近次之，尾梁和机腹下方最弱。

（4）直升机外部噪声具有明显的辐射特性，前下方30°方向噪声最为强烈，后下方次之，旋翼后行侧的噪声最弱。