螺钉装配应力及应力松弛对压力伺服阀零位影响
2021-06-26江裕雷朱玉川葛声宏周振锋
江裕雷,朱玉川,葛声宏,周振锋
(1.南京航空航天大学直升机传动技术国家级重点实验室,南京210016;2.中航工业南京机电液压工程研究中心航空机电系统综合航空科技重点实验室,南京210061;3.中航工业南京伺服控制系统有限公司,南京210032)
电液伺服阀因可将微弱电信号转换、比例放大为大功率液压动力输出,且具有体积小、动态响应快、控制精度高等显著特点,广泛应用于航空航天、舰船与兵器等国防装备电液伺服系统中[1]。作为电液伺服系统中的核心控制元件,其输出性能往往直接决定整个系统的静动态性能以及工作可靠性。
电液伺服阀具有电⁃磁⁃机⁃液多物理场耦合的复杂结构与性能耦合特性,且输入电驱动结构、磁路结构、先导液压放大结构和输出功率滑阀机械结构均具有对称结构特征,这种对称结构的对称精度与对称性的保持程度,直接决定伺服阀零位特性与零位稳定性,也是决定伺服阀及其系统可靠性的重要因素,由于伺服阀工作点始终位于零位附近,因此伺服阀输出性能和可靠性很大程度上需要依靠其零位稳定性加以保证[2]。
影响伺服阀零位稳定性的因素很多,诸如伺服阀零件加工误差、装配误差、装配应力、应力松弛、温度变化和振动冲击等[3],针对这些影响因素,国内外学者做了相关研究。
北京交通大学秦嘉言等[4⁃5]定量分析了温度对气隙磁阻和磁钢极化磁动势的影响,得到气隙长度随温度线性变化,极化磁动势接近线性变化。同济大学訚耀保等[6]通过建模分析得到一维离心环境下射流管伺服阀零偏值与离心加速度之间的正相关关系,并通过实验进行验证。武汉工程大学的熊仝[7]就射流管伺服阀零偏机理进行研究,发现零偏与伺服阀内应力有直接关系,而内应力产生的主要原因是焊接以及衔铁、支撑杆和螺钉等零件的装配。日本学者URATA[8⁃9]针对因加工和装配造成的工作气隙不对称情况,数学建模分析气隙左右不对称、垂直不对称和相对倾斜3种情况下的伺服阀零位变化。同济大学訚耀保等[10⁃11]在此基础之上,更为全面研究了射流管伺服阀气隙左右对称、上下对称、中心对称和单个气隙存在误差4种情况下伺服阀压力增益和流量增益变化。电液伺服阀具有结构对称特点,但由于零件加工误差、安装螺钉的应力松弛、安装螺钉的松动和温度变化等因素导致伺服阀工作气隙发生变化,造成结构不对称,甚至产生零偏,直接影响压力伺服阀的工作特性[12]。
这些研究表明影响伺服阀零位稳定性的因素具有多变量、非线性以及时变等特性,其中时变非线性特性的典型表现之一是伺服阀在加工完成搁置仓库一段时间或者服役一段时间后,常会发生零位变化,严重影响伺服阀的输出稳定性,这种变化的主要原因在于伺服阀部分零件与整体装配应力松弛[13],但是针对这种具有时变特性的研究,尤其定量研究,尚不多见。
本文以某型号压力伺服阀力矩马达的4个紧固螺钉为切入点,数值模拟螺钉装配应力以及装配应力松弛对力矩马达零位气隙的影响,进而建立电液压力伺服阀数学模型与仿真模型,仿真分析零位气隙变化对压力伺服阀前置级零位及喷嘴腔压力输出特性的影响规律,为伺服阀螺钉装配工艺改进、伺服阀后期维护提供理论支撑。
1 螺钉装配及应力松弛对气隙影响
螺钉联接是通过施加预紧力将异质构件联接在一起,在施加预紧力的同时会产生装配应力,应力长时间的作用下使得金属材料发生蠕变、应力松弛,使得预紧力降低[14]。应力松弛是指在恒定总应变条件下,随时间推移,应力不断减小的过程[15],如图1所示。应力松弛通常分为两个阶段,呈现显著非线性时变特性,在初始阶段,应力下降很快,持续时间不长,称为应力松弛第1阶段。之后应力缓慢降低且趋向一稳定值,形成稳定应力松弛阶段,称为应力松弛第2阶段,该阶段是应力松弛的主要阶段[16]。该过程既可存在于高温条件下,也存在于常温条件下,振动、温度和初始应力均是影响应力松弛速率的因素,因此这是一个复杂、多因素耦合的过程。

图1 应力松弛曲线Fig.1 Stress relaxation curve
如图2所示,在伺服阀力矩马达装配过程中,通常采用对角预紧4个螺钉将上导磁体、下导磁体、磁钢和阀体紧固。伺服阀输出特性受零位气隙影响显著,如图3所示,4个零位气隙由4个螺钉安装后上导磁体、下导磁体和衔铁的相对位置形成。在伺服阀非工作状态,当4个气隙完全相等或者气隙Ⅰ、Ⅱ,气隙Ⅲ、Ⅳ分别相等时,伺服阀处于零位,否则就会发生零偏。显然,4个螺钉的装配情况及其应力松弛将直接影响上导磁体、下导磁体和衔铁的相对位置,进而影响伺服阀力矩马达零位气隙与伺服阀零位稳定性。本节将基于ABAQUS有限元软件对螺钉装配应力以及装配应力松弛引起的零位气隙变化进行量化分析。

图2 力矩马达结构示意图Fig.2 Schematic diagram of torque motor’s structure

图3 零位气隙示意图Fig.3 Schematic diagram of zero air gaps
1.1 ABAQUS有限元仿真模型与参数确定
在ABAQUS有限元仿真软件中,对伺服阀力矩马达进行建模,设置材料参数、网格划分、接触设置以及施加预紧力。关键零件材料参数如表1所示。4个螺钉规格为M 2.5,公司技术人员在实际装配过程中使用的拧紧力矩为1.2 N·m,故由式(1)计算得到仿真施加理想预紧力值为1 600 N。

表1 关键零件材料参数Table 1 Material parameters of key parts

式中:T为拧紧力矩;d为螺纹公称直径;F0为预紧力;K为拧紧力矩系数,取0.3[17]。
1.2 螺钉装配应力对伺服阀力矩马达零位气隙影响
在ABAQSU载荷设置中,对力矩马达4个M 2.5螺钉同时施加1 600 N理想预紧力,对装配后力矩马达的装配应力及变形进行分析,分析结果如图4所示。其中图4(a)表示的是力矩马达装配后的变形,图4(b)表示的是力矩马达装配后的应力分布,最大装配应力为478 MPa,最大变形为45.3μm,同时可以看出零位气隙在螺钉装配应力的作用下发生改变。

图4 力矩马达装配后应力与变形分布云图Fig.4 Nephogram of stress and displacement after torque motor assembly
由于力矩马达衔铁处的4个零位气隙与伺服阀的零位特性直接相关,因此对上、下导磁体左右端面边缘上的装配变形位移进行提取作进一步的分析,其变形位移提取路径如图5所示,包括提取的边线及位移方向。

图5 上、下导磁体左右端面边缘变形位移提取路径Fig.5 Displacement extraction path of upper and lower magnetic body left and right end face edge deforma⁃tion
图6和7分别是力矩马达装配后上、下导磁体左右端面(1~12号边)的位移变化情况,该位移直接关乎气隙大小。可以间接得出:在4根螺钉装配应力作用下,上导磁体处气隙Ⅰ、Ⅱ减小22.6μm,下导磁体处气隙Ⅲ、Ⅳ减小2.87μm。因仿真模型考虑装配前伺服阀结构完全对称,所以导磁体左右两侧的位移变化规律一致。

图6 力矩马达装配后上导磁体两侧位移分布Fig.6 Displacement distribution on both sides of upper mag⁃netic body after torque motor assembly

图7 力矩马达装配后下导磁体两侧位移分布Fig.7 Displacement distribution on both sides of lower mag⁃netic body after torque motor assembly
1.3 螺钉装配应力松弛对伺服阀零位气隙影响
电液伺服阀在仓库贮存或者服役过程中,螺钉会发生装配应力松弛,造成预紧力降低,宏观表现为螺钉松动。仿真得到螺钉预紧力与螺钉最大应力峰值之间呈近线性关系,如图8所示。因此,为方便研究,本研究以预紧力降低来等效应力松弛现象,以相对于应力松弛前理想预紧力降低百分比来定量反映应力松弛程度,并以此为基础来研究应力松弛对伺服阀零位气隙以及伺服阀前置级喷嘴腔压力输出特性影响规律。

图8 力矩马达螺钉预紧力与其装配应力峰值关系Fig.8 Relationship between preload of torque motor screw and assembly stress peak
预紧力降低值取初始理想预紧力(1 600 N)的-10%、-20%、-30%。图9表示的是导磁体处联接螺钉的位置,4个螺钉分布于矩形4个顶点处,螺钉B预紧力降低用于模拟任意一个螺钉应力松弛。螺钉B、C预紧力降低用于模拟矩形短边两个顶点处螺钉应力松弛、螺钉A、B预紧力降低用于模拟矩形长边两个顶点处螺钉应力松弛、螺钉B、D预紧力降低用于模拟矩形对角线两个顶点处螺钉应力松弛。螺钉A、B、C预紧力降低用于模拟任意3个螺钉应力同时松弛。因此,本节重点分析螺钉B,螺钉B、C,螺钉A、B,螺钉B、D和螺钉A、B、C应力松弛导致力矩马达工作气隙变化规律,以模拟可能出现的力矩马达螺钉应力松弛全部工况,在分析指定螺钉预紧力降低时,其他螺钉预紧力保持理想预紧力1 600 N不变。

图9 力矩马达螺钉装配位置分布示意图Fig.9 Schematic diagram of assembly position distribution of torque motor screws
考虑到空气磁阻远大于导磁体磁阻,磁通会优先通过相对较小的气隙,所以在仿真中提取上、下导磁体左右端面上的最大位移(对应最小的气隙,即对应图5中的2、5、8、11号边)可以反映整个倾斜气隙截面上的磁路工作情况。图10~14中的零位气隙变化量均指的是相对于理想预紧力为1 600 N时的气隙变化。零位气隙Ⅰ、Ⅱ设计初始值为350μm,零位气隙Ⅲ、Ⅳ设计初始值为250μm,伺服阀输入额定电流后,零位气隙改变量即为衔铁最大偏转位移,根据本文压力伺服阀结构参数与仿真模型,仿真得到实际衔铁最大偏转位移为15.7μm。
1.3.1 螺钉B应力松弛
螺钉B应力松弛可以用于代替任意一个螺钉应力松弛的情况,在螺钉B装配应力相对于初始装配应力发生应力松弛10%~30%时,力矩马达4个零位气隙变化情况如图10所示。螺钉B预紧力降低30%至1 120 N,零位气隙Ⅰ减小0.77μm,减小量相当于衔铁最大偏转位移5%,零位气隙Ⅱ增加2.83μm,增加量18%,零位气隙Ⅰ、Ⅱ差值从0增大至3.6μm。

图10 螺钉B应力松弛对零位气隙影响Fig.10 Effect of screw B stress relaxation on zero air gap
零位气隙Ⅲ减小0.11μm,减小量相当于衔铁最大偏转位移0.7%,工作气隙Ⅳ增加了0.37μm,增量2%,零位气隙Ⅲ、Ⅳ差值从0增大至0.48μm。
1.3.2 螺钉B、C应力松弛
螺钉B、C应力松弛可以用于模拟矩形短边两个顶点处螺钉应力松弛情况,结合图9所示,由于螺钉B、C位于右侧,所以上下导磁体右侧工作气隙Ⅱ、Ⅳ随预紧力降低线性增加,如图11所示。

图11 螺钉B、C应力松弛对零位气隙影响Fig.11 Effect of stress relaxation of screws B and C on zero air gap
螺钉B、C预紧力降低30%至1 120 N,零位气隙Ⅰ减小量相当于衔铁最大偏转位移9%,零位气隙Ⅱ增加量46%,零位气隙Ⅰ、Ⅱ差值从0增加至8.65μm;零位气隙Ⅲ减小量相当于衔铁最大偏转位移0.9%,零位气隙Ⅳ增加量5%,零位气隙Ⅲ、Ⅳ差值从0增大至0.99μm。
1.3.3 螺钉A、B应力松弛
螺钉A、B应力松弛可以用于模拟矩形长边两个顶点处螺钉应力松弛情况,由于螺钉A与螺钉B在空间位置上左右对称,当这两螺钉发生应力松弛,零位气隙Ⅰ、Ⅱ变化一致,零位气隙Ⅲ、Ⅳ变化一致,如图12所示。随螺钉A、B预紧力降低30%至1 120 N,零位气隙Ⅰ、Ⅱ增加量相当于衔铁最大偏转位移16%,其差值一直为0,零位气隙Ⅲ、Ⅳ增加量2%,其差值也一直为0。

图12 螺钉A、B应力松弛对零位气隙影响Fig.12 Effect of stress relaxation of screws A and B on ze⁃ro air gap
1.3.4 螺钉B、D应力松弛
螺钉B、D应力松弛可以用于模拟矩形对角线两个顶点处螺钉应力松弛情况,螺钉B与螺钉D在空间位置上中心对称,当两螺钉发生应力松弛,对上下导磁体左右两侧端面气隙影响一致,如图13所示。螺钉B、D预紧力降低30%至1 120 N,零位气隙Ⅰ、Ⅱ增量相当于衔铁最大偏转位移13%,其差值一直为0,零位气隙Ⅲ、Ⅳ增加量2%,其差值也一直为0。

图13 螺钉B、D应力松弛对工作气隙影响Fig.13 Effect of stress relaxation of screws B and D on ze⁃ro air gap
1.3.5 螺钉A、B、C应力松弛
螺钉A、B、C预紧力降低可以用于模拟任意3个螺钉应力同时松弛情况,随螺钉A、B、C预紧力降低30%至1 120 N,零位气隙变化如图14所示。零位气隙Ⅰ增加量相当于衔铁最大偏转位移11%,零位气隙Ⅱ增加量44%,零位气隙Ⅰ、Ⅱ差值从0增加至5.19μm;零位气隙Ⅲ增加量相当于衔铁最大偏转位移1.6%、零位气隙Ⅳ增加量5%,零位气隙Ⅲ、Ⅳ差值从0增加至0.53μm。
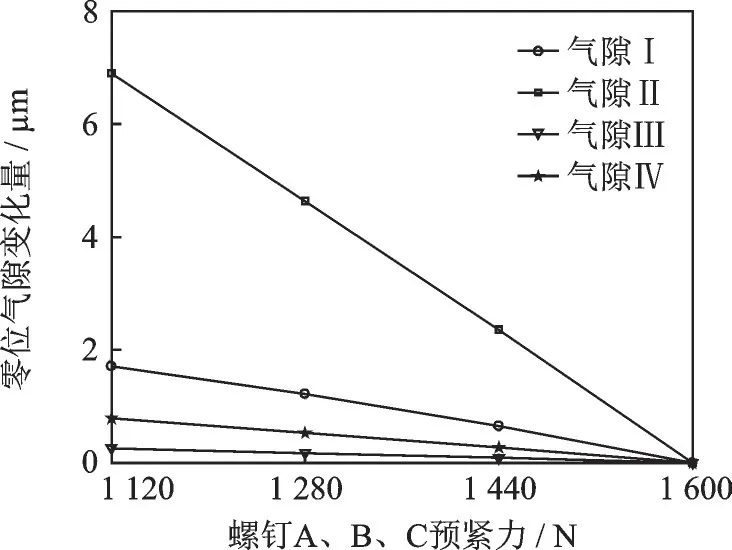
图14 螺钉A、B、C应力松弛对零位气隙影响Fig.14 Effect of screws A,B and C stress relaxation on ze⁃ro air gap
2 电液压力伺服阀数学模型建立
为进一步分析螺钉应力松弛导致的气隙变化对压力伺服阀零位特性与前置级喷嘴腔压力输出特性的影响规律,需要建立电液压力伺服阀数学模型。
2.1 力矩马达磁路数学模型建立
在伺服阀力矩马达的磁路特性研究中,一般采用简化磁路结合基尔霍夫定律进行分析,如图15所示。
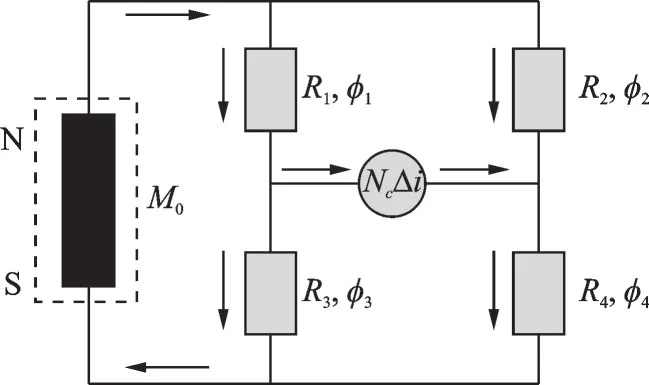
图15 力矩马达简化磁路Fig.15 Simplified magnetic circuit of torque motor

式中:Ri为气隙处磁阻;ϕi为气隙磁通量(i=1,2,3,4);M0为永磁体的极化磁动势;Nc为线圈匝数;Δi为控制电流,本文取9 mA。
气隙磁阻可以根据式(3)计算得到

式中:μ0为空气磁导率,值为4π×10-7;g为气隙长度;Ag为垂直磁通的磁极面积。
在电磁力的作用下衔铁受到的电磁转矩Td为

式中a为衔铁由转轴到导磁体工作面中心的半径。
2.2 衔铁组件运动学数学模型建立
随着挡板的移动,挡板逐渐偏离中位,喷嘴中心线挡板处的位移xf可表示为

式中:r为衔铁组件偏转中心至喷嘴中心的距离;θ为衔铁组件质心偏转角度。
挡板工作时受左右喷嘴液压力F1、F2作用而产生力矩Tnozzle[18],如图16所示。其中液压力可以分为两部分:(1)以喷嘴孔直径DN为圆的区域,可认为是静压,值为p1或者p2;(2)以喷嘴孔直径DN为内径,挡板直径为外径的环状区域,该部分压力呈对数分布,当喷嘴与挡板的距离很小时,可认为该部分的压力值是挡板腔的压力值p0。

图16 前置级喷嘴挡板示意图Fig.16 Schematic diagram of nozzle flapper
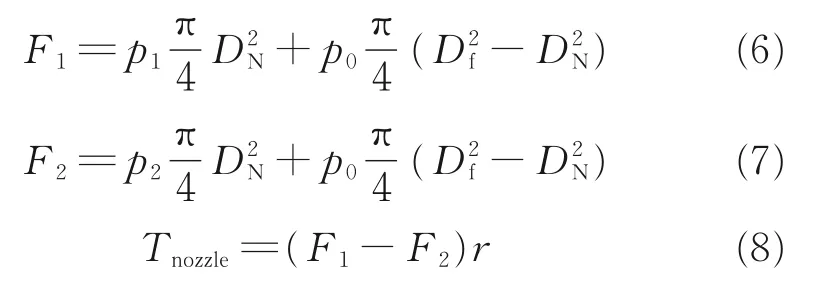
式中:p1、p2分别为左右喷嘴腔压力;p0为回油腔压力;DN为喷嘴直径;Df为挡板直径;Tnozzle为油液对挡板净作用力矩。
当然在衔铁的运动过程中,弹簧管发生弯曲,由于变形而产生的力矩为

式中ktube为弹簧管的扭转刚度。
对衔铁组件应用刚体定轴转动定律,假定挡板与喷嘴之间不会发生触碰,受电磁力作用,衔铁组件的运动学方程可表示为
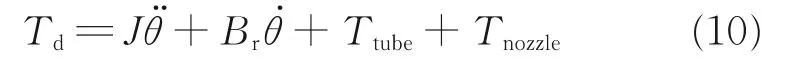
式中:J为衔铁组件转动惯量;Br为衔铁组件阻尼。
2.3 喷嘴挡板阀数学模型建立
喷嘴挡板阀由喷嘴、固定节流孔以及挡板组成,通过节流孔流量方程可推导该处流量与压力之间的关系,因此通过左右两个固定节流孔的流量Q1、Q2可以表示为
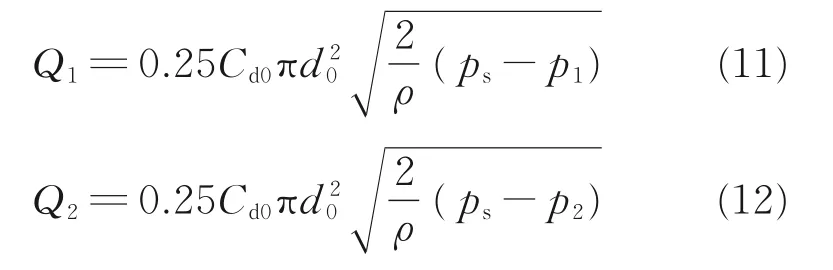
式中:Cd0为节流孔流量系数,本文取0.76;d0为节流孔的直径;ps为供油压力;ρ为液压油的密度。
同样,也可通过喷嘴流量方程推导该处流量与压力之间的关系,经过左右两个喷嘴的流量Q3、Q4可以表示为

式中:Cdf为喷嘴处流量系数,本文取0.76;xf0为挡板在中位时,喷嘴与挡板之间距离。
考虑到滑阀两端油液的压缩性以及阀芯处的内外泄漏,根据流量连续性方程,喷嘴挡板级的动态可表示为[19]

式中:Av为滑阀的端面积;Ci为阀芯内漏系数;Ce为阀芯外漏系数;V1、V2为左右喷嘴腔容积;βe为液压油有效体积模量;xv为阀芯位移。
2.4 滑阀数学模型建立
电液压力伺服阀的反馈机制是靠密闭容腔的压力作用在滑阀反馈端面上形成力反馈,进油口阀口流量为Qin,出油口阀口流量为Qout。

式中:Cf为滑阀节流边流量系数,本文取0.7;pf为反馈压力;Vf为密闭容腔体积;xl为滑阀工作点位置,当xv大于xl,阀口进油,否则出油;dv为滑阀直径。
滑阀的动态方程可表示为

式中:mv为阀芯及阀腔油液质量;cv为阻尼系数;kv为稳态液动力刚度;Af为反馈面面积。
3 伺服阀零位与工作特性分析
为了进一步分析4个零位气隙不均等变化对伺服阀前置级零位特性和工作特性的影响,结合电液压力伺服阀的数学模型,在MATLAB/Simulink中搭建整阀非线性集总参数仿真模型,如图17所示,分析力矩马达螺钉装配应力及不同位置螺钉装配应力松弛引起的4个零位气隙变化对伺服阀前置级两喷嘴腔压差影响,仿真参数如表2所示。

图17 压力伺服阀仿真模型Fig.17 Simulation model of pressure servo valve

表2 压力伺服阀仿真参数Table 2 Simulation parameter s of pressur e servo valve
3.1 螺钉装配对伺服阀零位及工作特性影响
力矩马达A、B、C、D 4个螺钉在1 600 N的预紧力作用下,气隙Ⅰ、Ⅱ、Ⅲ、Ⅳ同时减小,对伺服阀零位及工作特性影响如图18所示。文中所提及的零位压差指的是两喷嘴腔0电流时的输出压差,工作压差指两喷嘴腔额定电流工作时的输出压差。

图18 压差随仿真时间变化曲线Fig.18 Curves of pressure differential changing with simula⁃tion time
在0~0.05 s内,控制电流是0,对应压差是零位压差,0.05~0.1 s内,额定电流为10 mA,额定输入压力21 MPa,对应压差是工作压差。从图18中可知理想螺钉装配前后零位压差都是0,在没有施加预紧力之前,工作压差为2.485 MPa,施加预紧力之后,工作压差增大了0.363 MPa。由此可以看出在理想的装配应力下,不会产生零偏,但会影响工作压力增益。
3.2 螺钉装配应力松弛对零位及工作特性影响
第1节通过有限元仿真分析得到不同位置螺钉应力松弛下伺服阀气隙的变化规律,结合第2节建立的压力伺服阀集总参数模型,进一步分析螺钉B,螺钉B、C,螺钉A、B,螺钉B、D以及螺钉A、B、C应力松弛对伺服阀的零位特性以及工作压差的影响规律。
图19是不同位置螺钉应力松弛对零偏的影响曲线。零偏一般用为使伺服阀处于零位所输入的电流与额定电流的百分比表示。在螺钉B应力松弛30%,会导致1.9%的零偏,螺钉B、C应力松弛30%,导致4.6%的零偏,螺钉A、B、C应力松弛30%,导致2.8%的零偏。然而螺钉A、B及螺钉B、D预紧力变化未引起零偏,是因为螺钉A、B左右对称,螺钉B、D中心对称。

图19 螺钉应力松弛与零偏关系Fig.19 Relationship between screw stress relaxation and ze⁃ro position
不同位置螺钉应力松弛对工作压差的影响如图20所示,5种不同位置的螺钉应力松弛均会引起工作压差的变化。其中螺钉B预紧力降低30%至1 120 N,工作压差增加1.4%;螺钉B、C预紧力降低30%至1 120 N,工作压差增加3.2%;螺钉A、B预紧力降低30%至1 120 N,工作压差减少1.4%;螺钉B、D预紧力降低30%至1 120 N,工作压差减少1.1%;螺钉A、B、C预紧力降低30%至1 120 N,工作压差增加0.4%。

图20 螺钉应力松弛对工作压差影响Fig.20 Influence of screw stress relaxation on working pres⁃sure difference
4 结 论
通过在ABAQUS中建立压力伺服阀力矩马达有限元模型,仿真得到力矩马达螺钉装配及不同位置螺钉装配应力松弛导致的工作气隙变化规律,建立压力伺服阀非线性集总参数数学模型,在MATLAB/Simulink中仿真得到力矩马达螺钉装配应力及应力松弛导致的压力伺服阀零偏、前置级输出压差变化规律,为伺服阀制造工艺改进以及服役零位故障诊断提供理论支撑。
(1)压力伺服阀力矩马达螺钉装配应力导致4个零位气隙发生变化。由于力矩马达结构对称,4个零位气隙的变化也具有对称性,因此,如果伺服阀装配前处于零位,则螺钉装配不会使伺服阀发生零偏,但会使两喷嘴腔工作压差增大。
(2)压力伺服阀力矩马达4个矩形分布螺钉中,任意长边侧分布的两个螺钉松弛或任意对角线分布的两个螺钉松弛,将导致力矩马达4个零位气隙均增大,但增大的气隙具有左右对称相等的特征,不会引起零偏,但会使两喷嘴腔工作压差减小。
(3)压力伺服阀力矩马达4个矩形分布螺钉中,任意单个螺钉松弛,任意3个螺钉或者任意短边侧分布螺钉应力松弛将导致该螺钉所在侧零位气隙增大,非螺钉所在侧零位气隙减小,同时由于左右两侧零位气隙变化方向与数值均不同,所以会发生零偏,且会使两喷嘴腔工作压差增大。
(4)在所研究的5种螺钉松弛工况中,短边侧分布螺钉应力松弛造成的零偏最为显著,当其应力松弛30%,4个零位气隙中,最大增量相当于衔铁最大偏转位移46%,同时导致4.6%的零偏以及两喷嘴腔工作压差增加3.2%。
(5)研究结果表明,在压力伺服阀装配过程中尽量通过自动化拧紧设备保证4个螺钉预紧力与装配应力一致,在螺钉装配完成后有必要加速装配应力释放,并采取有效的螺纹防松工艺措施,以防止伺服阀服役过程中发生应力松弛导致伺服阀零偏。
