融合相似度图和随机游走模型的多标签短文本分类算法*
2021-06-25李晓红王闪闪马堉银马慧芳
李晓红,王闪闪,马堉银,马慧芳
(西北师范大学计算机科学与工程学院,甘肃 兰州 730070)
1 引言
传统的单标签分类学习是指每一个样本实例拥有唯一的一个类别标签,其中每一个标签属于一个互斥的标签集合L(|L|>1)。但是,在实际应用中,普遍存在一条数据可能同时属于多个不同类别的情况,这类数据被称作多标签数据[1],比如,一篇新闻报道可以同时属于“娱乐”类别和“科技”类别,一部影片可以同时属于“动作片”和“惊悚片”。和传统的单标签分类问题相比,多标签分类问题存在着显著的区别,类别间的相关性和共现性直接导致传统的单标签分类方法无法被直接应用到多标签分类问题中,多标签分类问题正逐渐成为当前的研究热点和难点,在文本分类、定向营销、基因功能分类和图像语义注释等领域中的应用尤为广泛。
多标签分类问题需要寻找最优的分类算法从而提高多标签数据的分类精度。目前,多标签分类最常见的思路有2种[2]。一种是问题转换,就是将多标签数据集转换成单标签数据集,然后用传统的单标签数据分类算法对转换后的数据进行分类。BR(Binary Relevance)[3]是一种典型的问题转换算法,它将每个标签的预测看作是一个独立的单分类问题,并为每个标签训练一个独立的分类器,用所有训练数据对每个分类器进行训练。但是,这种算法忽略了标签之间的相互关系,往往无法达到令人满意的分类效果。文献[4]提出了一种针对DBR(Dependent Binary Relevance)的修剪方法,使用Phi系数函数来估计标签之间的相关度,以去除不相关的标签。Liu等[5]提出一种基于动态规划的分类器链CC-DP(Classifier Chain-Dynamic Programing))算法和贪婪的分类器链(CC-Greedy)算法搜索全局最优的标签,弥补了CC(Classifier Chain)算法[6]对标签选择敏感的缺陷。另一种思路是改进算法,即改进已有单标签学习算法以解决多标签学习问题。如ML-KNN算法[7]通过统计得出每个标签的先验概率,对标签集合Y中的每个标签λ,分别计算样本x有标签λ和没有标签λ的概率,进而预测x是否具有标签λ。Tsoumakas等[8]提出RAkEL (RAndom k labELsets)方法将初始标签集分解为若干个小的随机子集,并利用Label Powerset算法[9]训练分类器。除此之外,其他研究者也利用各种方法进行多标签分类的研究[10,11]。
考虑到目前已有的多标签分类算法在数据预测训练模型过程中,要么忽略类别标签之间的相互依赖关系,要么忽略初始特征对预测值的重要影响,甚至把这些标签作为附加特征增加到原始特征集中,使得本来维数就很高的特征集更加复杂。即使考虑了类别标签之间的依赖关系,也往往不能充分利用这种关系,且多标签分类算法忽略标签集合与训练集合之间的初始预测值,使得多标签分类不准确。本文针对这些问题,提出一种融合相似度图和重启随机游走模型的多标签分类SGaRW (multi-label classification algorithm combining Similarity Graph and Random Walk)算法。一方面,利用相似度图充分计算文本与标签之间的关系,另一方面利用重启随机游走模型挖掘标签与标签之间潜在的语义联系,最后再进行合理的融合,使得多标签分类结果更准确。
2 相关工作
2.1 多标签分类
从本质上讲,多标签分类可被看作是一个标签排序问题[12]。根据测试样本与每个类别标签之间的相关度对其进行打分,然后按照分值的高低来决定样本所隶属的标签。
设X={x1,x2,…,xn}表示样本集合,Y={y1,y2,…,ym}表示标签集合,训练集合表示为D={(xi,Yi)|1≤i≤n},其中xi∈X为d维的样本向量(xi1,xi2,…,xid),而Yi⊆Y是样本xi所属的标签集合。因此,对样本x的标签预测可以表示成如下所示的向量H(x):
H(x)=(s1(x),…,si(x),…,sm(x))
(1)
其中,si(x)∈[0,1]描述样本x与标签yi之间的相关度。多标签分类就是从训练数据中学习得到一个多标签分类器h:X→2Y,对于给定的任意新样本x,分类器能预测该样本隶属的标签集合。
因此,多标签分类就是寻找较优的分类算法来构造高精度的分值向量H(x),从而达到准确分类的目的。本文提出了融合相似度图和重启随机游走模型的算法SGaRW实现文本的多标签分类,该算法分2个阶段实现:第1阶段创建相似度图,计算文本与标签集合之间的初始预测值向量H(x);第2阶段构建标签依赖关系图,在此图上执行重启随机游走算法,挖掘标签之间潜在的语义关系,算法收敛时即可得到文本隶属各个标签的概率向量。
2.2 基于语义网WordNet的相似度图
基于Wordnet3.0构建的相似度图[13,14]是一个有向加权图G1=〈V1,E1〉,用来计算图中顶点之间的语义相似度。其中,V1=itemsset∪senseset,itemsset集合由表示词项的节点item构成,senseset集合由表示含义的节点sense构成。含义节点之间、含义节点与词项节点之间以及词项节点之间连有向边〈vi,vj〉∈E1,边上的权重记为wij。如图1所示,itemsset={adventure,thriller,action},senseset={“document with 100 non-noise words ‘adventure’ appearing 2 times and the ‘Thriller’ appearing 1 time and the word ‘love’ appearing 1 time”,“a wild and exciting undertaking lawful”,“take a risk hope of…”,“something that people do or cause to happen” }。从节点“adventure”指向第1个含义节点的权值表示某人需要单词“adventure”的信息,那么他对该词的第1个含义节点感兴趣的概率是0.92。而由含义节点指向节点“adventure”的权值为1,即某人看到含义节点中的任意一个,一定会想到单词“adventure”。 所以,相似度图又可以称为概率图,边〈vi,vj〉反映了一种条件概率,表示看到当前节点vi的条件下联想到节点vj的概率。
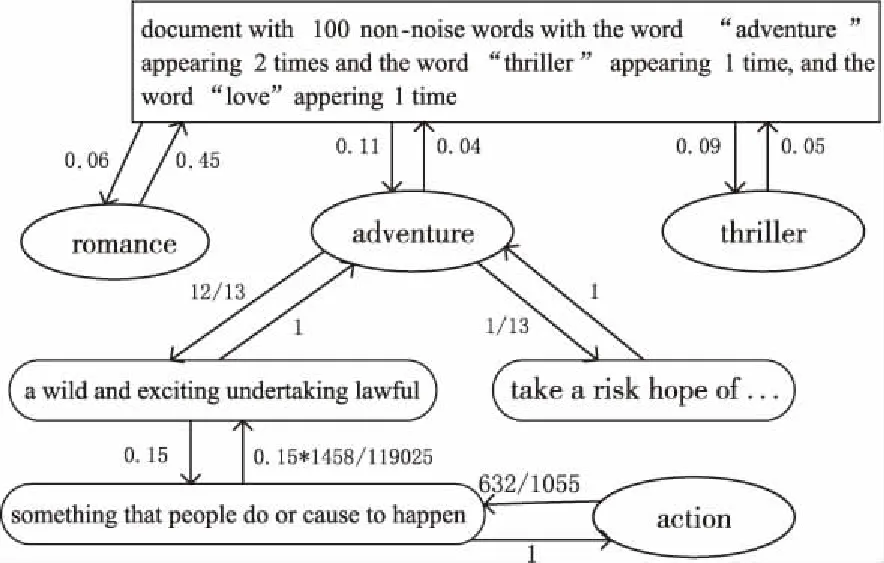
Figure 1 Similarity graph based on WordNet
2.3 重启随机游走模型
重启随机游走模型RWR(Random Walk with Restart)[15]是遍历图的一个随机过程,其基本思想是:从一个或一系列顶点开始遍历一个图,在任意一个顶点,遍历者将以概率1-α随机选择与该顶点相邻的顶点,或以概率α随机跳跃到图中的任何一个顶点,每次游走后得到的概率分布刻画了图中每个顶点被访问到的可能性,反复迭代这一过程直到收敛于一个稳定的概率分布。其数学表示为:
Pt+1=(1-α)·C·Pt+α·Q
(2)
其中,Pt表示第t步时达到的概率分布向量;C是概率转移矩阵;α是重启因子,即直接回到出发顶点的概率;Q是重启向量,本文对应为初始预测向量。
3 多标签文本分类算法设计
本文提出的多标签分类算法SGaRW分为2个阶段。第1阶段根据文本内容创建相似度图,计算文本与标签集合之间的初始预测值H(x);第2阶段构建标签依赖图,并在此图上进行随机游走,挖掘标签集合间的潜在关系。当游走概率趋于稳定时,即可得到文本的预测标签集合。
3.1 样本与标签集合之间的初始预测值
本文将一篇短文本看作一个含义节点,训练文本的各个标签映射为词项节点,创建相似度图,则任意短文本与标签之间的相似性可用式(3)和式(4)计算:
cor(vdoc,vlabel)=∑Apt(vdoc|vlabel)
(3)
Apt(vdoc|vlabel)=∏P(vi|vj)
(4)
其中,节点序列pt=〈vdoc,…,vi,vj,…,vlabel〉表示从vdoc到vlabel的一条有向简单路径,ppt(vi|vj)是相似度图上vi和vj之间边上的权重,用于计算2节点之间的亲密程度。Apt(vdoc|vlabel)表示vdoc到vlabel在简单路径pt上的亲密程度。根据马尔可夫模型,Apt(vdoc|vlabel)是该有向路径上所有相邻边上权值的乘积。所以,图中vdoc和vlabel的单向相关性就是从节点vdoc到节点vlabel的所有路径上Apt(vdoc|vlabel)之和。随着路径长度增加,条件概率的值将减小,路径越长,2个节点亲密的程度越小。
接下来,本文使用均值度量2个节点之间的相似性:
correlation(vdoc,vlabel)=
(5)
经过以上步骤,即可得到样本x与某标签yi之间的初始预测值,记为hi(x),即:
hi(x)=correlation(x,yi)
(6)
考虑所有的标签,即可得到样本x与标签集合Y的相关分数,如式(7)所示:
H(x)=[h1(x),h2(x),…,hm(x)]T
(7)
3.2 在标签依赖图上随机游走
3.2.1 标签与标签之间的依赖关系
本文使用图2所示的无向图来编码标签之间的依赖关系,记为G2=(V2,E2),其中,V2是数据集上所有标签构成的节点集合,E2是边集,若标签yi和yj同时标记文本x,则在yi和yj之间增加一条边。边上的权值记为wij,定义为同时拥有标签yi和yj的文本个数,如式(8)所示:
(8)

Figure 2 Label graph
无向图G2的邻接矩阵S是q×q的对称矩阵,如图3所示,q是标签依赖图中的顶点数。本文用式(9)对其进行非对称处理:
(9)
其中,sij是邻接矩阵S中的元素,sj是S中第j列所有元素之和。得到非对称化的邻接矩阵如图4所示。

Figure 3 Adjacency matrix

Figure 4 Asymmetric adjacency matrix
3.2.2 标签依赖图上的随机游走
由于每一个标签的预测在一定程度上能传播到其他标签上,因此,与样本有关的标签预测不仅由样本自身的特征决定,也会通过其他标签的预测被加强,标签的预测会经过多次更新而不是被预测模型直接决定。本文利用在PageRank中的简单策略重写式(2)得到式(10):
(10)
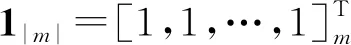
为了直观地说明本文算法分类的过程,以图1所示相似度图的一部分为例进行说明。
首先根据式(3)和式(7)可以计算预测样本doc与各个标签之间的单向相似性及标签的初始预测值:
cor(vdoc,vadventure)=0.11,cor(vadventure,vdoc)=0.04,hadventure(vdoc)=0.075。
同样可以得到:hthriller(vdoc)=0.07,haction(vdoc)=0.075,hraomance(vdoc)=0.06。
因此,样本doc与标签集合的相关分数H(doc)=(0.075,0.07,0.075,0.06)T。
然后再根据标签依赖图计算状态转移矩阵S(如图4所示)。若α= 0.15,P= (0.25,0.25,0.25,0.25)T。
按照式(10)迭代直至满足收敛条件,得到:
P(Y)doc=(0.68752828,0.3993173,0.1124934, 0.80029032)T
由此可知,样本doc最可能的标签是adventure和thriller。
4 实验结果与分析
4.1 数据集
为了验证本文算法的分类性能,使用2个多标签分类文本数据Movies 和 AAPD(Arxiv Academic Paper Dataset)进行实验,其中标签密度[1]表示每个样本的平均标签数。
Movies来自IMDB实验室人工采集的2 011条英文电影简介和对应的36个主题标签,标签密度为2.97。
AAPD数据集收集了计算机科学领域的55 840篇论文摘要和对应的54个主题标签,标签密度为2.41。
4.2 评价标准
传统的单分类算法性能评价指标,如查全率、查准率无法直接用于评价多标签算法的分类性能。因此,本文将采用以下3种指标来衡量所提算法的性能。
(1)汉明损失(Hamming Loss)。
汉明损失[16]是评估误分类的实例-标签对多少的一种评价指标,即属于该样本的标签未出现在该类标签集合中而不属于的标签却出现。该指标的值越小,表示分类性能越优,其值为零时性能最优(公式和实验部分简记为H_loss)。
(11)
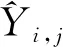
(2) 杰卡德相似系数(Jaccard Index)。
杰卡德相似系数[17]用来度量2个集合之间的相似性,它被定义为2个集合A和B交集的元素个数除以并集的元素个数。该指标取值越大,分类性能越优,当其取值为1时性能最优。
(12)
(3) 精确度(Accuracy)。

(13)
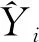
4.3 实验结果
为了评测本文算法在多标签文本分类方面的性能,精心设计了以下3个实验:(1)选择不同的随机游走收敛阈值α进行实验,验证不同的α得到不同的实验结果,并确定最优的α值;(2) 使用不同大小的训练数据和测试数据进行实验,验证数据规模对实验结果的影响;(3)将本文算法与其他不同的多标签分类算法进行对比。
实验1不同的α对实验的影响。
本实验在Movies数据集上采用留一法进行,验证不同的α会得到不同的分类性能。具体地,随机抽取1个样本作为测试集,剩余的2 010条数据全部作为训练集,总共抽取了600次测试数据,最后将得到的600组实验的平均值作为最后的结果进行分析。在每组实验中,参数α分别取0.000 1,0.000 07,0.000 04,0.000 01进行实验,结果如表1所示。
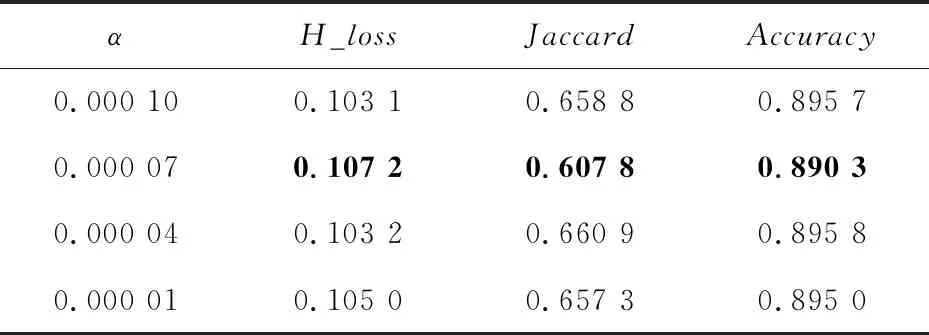
Table 1 Experimental results with different α
由表1可以看出,α=0.00007时H_loss和Jaccard这2个指标都达到了最大值,Accuracy略微低一点。总体来看,综合性能指标最优,因此在后面的2个实验中,α的值均设定为0.000 07。
由表2可以看出,当测试集的大小为500,训练集v的大小为1 500时,其H_loss和Jaccard均达到最好的情况,Accuracy略低。另外,为了表现其他指标的正比例增长趋势所反映的含义,在图5中绘制了1-H_loss的值来体现算法性能。 AAPD数据集上的实验结果如图5所示,随着训练集规模不断增大,1-H_loss的值不断减小,但是降低程度不明显。而杰卡德相似性系数和准确率不断增加。当训练集规模为40 000时,上升趋势趋于平稳。总体来看,测试集规模为1 000时得到的实验结果比测试集规模为3 000 时的实验结果好。

Table 2 Experimental results on Movies
实验2数据集的规模对实验结果的影响。
因汉明损失是用于量化基于单个标签的分类误差,该指标的值越小,表示分类性能越优。
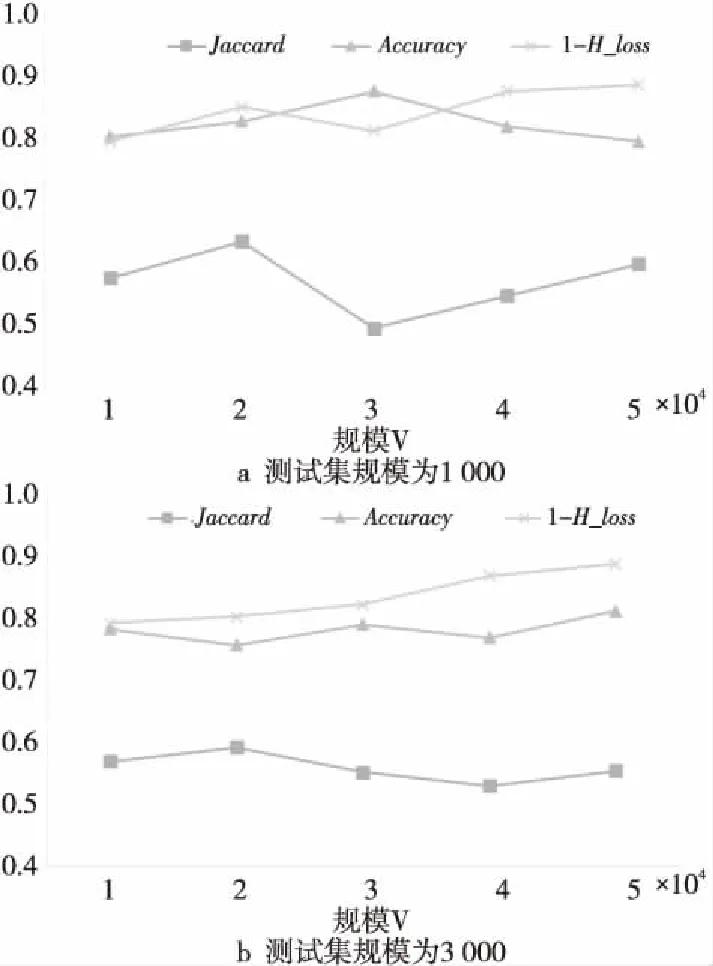
Figure 5 Experimental results on AAPD
实验3不同算法的性能对比。
本文选择与BR、ML-KNN、CC、CLLIFT[19]和LSFLC[20]等算法进行对比。其中,ML-KNN 中k=20,CLLIFT中比率参数δ设置为0.1,其他均采用算法的默认参数。各算法在AAPD数据集上的结果如图6所示。
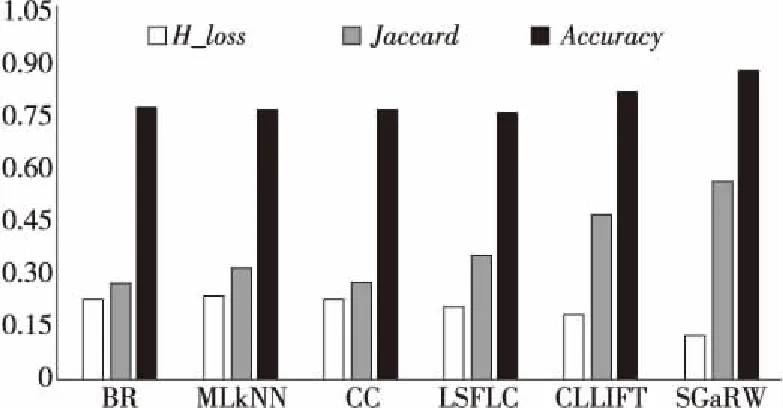
Figure 6 Performance comparison of each algorithm on AAPD
从图6可以看出,不论是Accuracy值,还是汉明损失值和杰卡德相似度值,SGaRW算法实现多标签分类的效果是最好的。CLLIFT尽管也考虑了标签信息,但仅仅作为辅助信息,而SGaRW则是通过在标签依赖图上进行随机游走,考虑了标签与标签之间潜在的语义联系。并且,SGaRW算法使不属于该文本的标签尽量少地出现在标签集合中,从而降低错误率。只是在AAPD数据集上,由于数据稠密的特性,SGaRW算法与BR、ML-KNN、CLLIFT等算法在Accuracy指标上的差异度略小。
5 结束语
本文提出了一种融合相似度图和随机游走模型的多标签分类算法SGaRW,能够有效解决短文本多标签分类问题。算法利用外部知识库WordNet提供的先验信息构建相似度图,在其上计算标签与文本之间的初始匹配值;然后基于数据的已有标签建立标签依赖图,并在图上执行重启随机游走,最终确定预测文本的类别标签。由于SGaRW算法中相似度图的构建只考虑了名词、动词和形容词这几种主要实例,造成部分辅助信息的丢失,学习过程加长,可能会降低最终的分类精度。下一步研究的重点将考虑增加数据集规模,引入短文本语义理解、句法分析等技术来提升短文本多标签分类性能,也会考虑进一步优化算法。
