PCA-FSA-MLR模型及在径流预测中的应用研究

2021-06-25郭存文崔东文

人民珠江 2021年6期

郭存文，崔东文

(1.云南省水文水资源局文山分局,云南文山 655000；2.云南省文山州水务局,云南文山 663000)

1 研究背景

研究提出具有较好预报精度的模型及方法一直是水文学领域研究的重点和热点。目前，用于径流预报的方法有BP[1-2]、GRNN[3]、Elman[4]、RBF[5]等人工神经网络法以及多元回分析法[6-7]、集对分析法[8]、灰色预测法[9]、支持向量机法[10-11]、投影寻踪回归法[12]、小波分析法[13]、随机森林法[14-15]、组合预测法[16-17]等，均在径流预测中获得较好的预测效果。多元线性回归(multiple linear regression，MLR)虽已在径流预测中得到应用[7]，但存在以下问题和不足：①MLR对异常值敏感，预测精度不高；②影响因子(变量)较多时难以精确估计MLR常数项和偏回归系数，目前普遍采用最小二乘法(least squares，LS)估计MLR相关参数，但LS求解方法复杂且精度不高。

为消除MLR受异常值的影响，精确估计MLR常数项和偏回归系数，提高MLR模型预测精度，本文提出建立基于主成分分析(principal component analysis，PCA)、未来搜索算法(Future search algorithm，FSA)、MLR多种策略相融合的PCA-FSA-MLR径流预测模型。首先利用PCA对样本数据进行降维处理，使数据样本简洁且更具代表性，以消除异常值对MLR的影响；其次选取8个标准测试函数在5维、10维、20维、30维、100维和500维条件下对FSA进行仿真测试，以检验FSA能否满足MLR常数项和偏回归系数的寻优要求；最后利用FSA对MLR常数项和偏回归系数进行寻优，建立PCA-FSA-MLR预测模型，并将该模型应用于云南省龙潭站年径流及同年枯水期12月月径流预测，预测结果与经PCA降维处理的PCA-LS-MLR、PCA-FSA-支持向量机(support vector machines，SVM)、PCA-SVM模型和未经降维处理的FSA-MLR、LS-MLR、FSA-SVM、SVM模型作对比，以检验PCA-FSA-MLR模型的预测性能和预测效果。

2 PCA-FSA-MLR预测模型

2.1 主成分分析法

主成分分析(PCA)是一种通过降维技术把多个变量化为少数几个主成分的多元统计方法。设具有n个变量(x1,x2,…,xn)、k个样本的数据矩阵为[18-19]：

(1)

式中，Xi=[x1ix2i…xki]T。

(2)

式中F1、F2、Fm——第一主成分、第二主成分、第m主成分；aij——主成分系数。

2.2 未来搜索算法(FSA)

2.2.1FSA数据描述

未来搜索算法(FSA)是M.Elsisi[20]于2018年通过模仿人类向往美好生活而提出的一种新颖搜索算法。该算法通过建立数学模型模拟人与人之间最优生活(局部搜索)和历史最优生活(全局搜索)来获得最优解。与其他算法相比，FSA具有调节参数少、收敛速度快、寻优能力强等优点。参考文献[20]，FSA数学描述简述如下：

a)算法初始化。FSA通过式(3)初始化当前解：

S(i,:)=Lb+(Ub-Lb)*rand(1,d)

(3)

式中S(i,:)——第i个国家/地区当前解；Ub、Lb——搜索空间的上、下限；rand——均匀分布随机数；d——问题维数。

b)局部解和全局最优解。FSA将每个国家/地区当前最优解定义为局部最优解LS，将所有国家/地区当前最优解定义为全局最优解GS，并通过迭代过程获得待优化问题最优解。FSA通过式(4)、(5)实现局部解和全局最优解的更新：

S(i,:)L=(LS(i,:)-S(i,:))*rand

(4)

S(i,:)G=(GS-S(i,:))*rand

(5)

式中S(i,:)L、S(i,:)G——第i个国家/地区局部解和全局最优解；LS(i,:)——第i个国家/地区局部最优解；GS——所有国家/地区全局最优解；rand——[0,1]范围内随机数。

c)定义新解。在获得第i个国家/地区局部解和全局最优解后，利用式(6)重新定义当前解：

S(i,:)=S(i,:)+S(i,:)L+S(i,:)G

(6)

d)更新随机初始值。FSA在更新局部最优解LS和全局最优解GS后，利用式(7)更新式(3)的随机初始值：

S(i,:)=GS+[GS-LS(i,:)]*rand

(7)

2.2.2FSA仿真测试

参考文献[21-23]，选取Spher等8个典型测试函数在5维、10维、20维、30维、100维和500维条件下对FSA进行仿真验证。单峰函数主要测试FSA的寻优精度，多峰函数主要测试FSA的全局搜索能力，并利用20次寻优平均值对FSA寻优性能进行评估，见表1。FSA参数设置：最大迭代次数T=1000，种群规模N=50，其他参数采用FSA默认值。

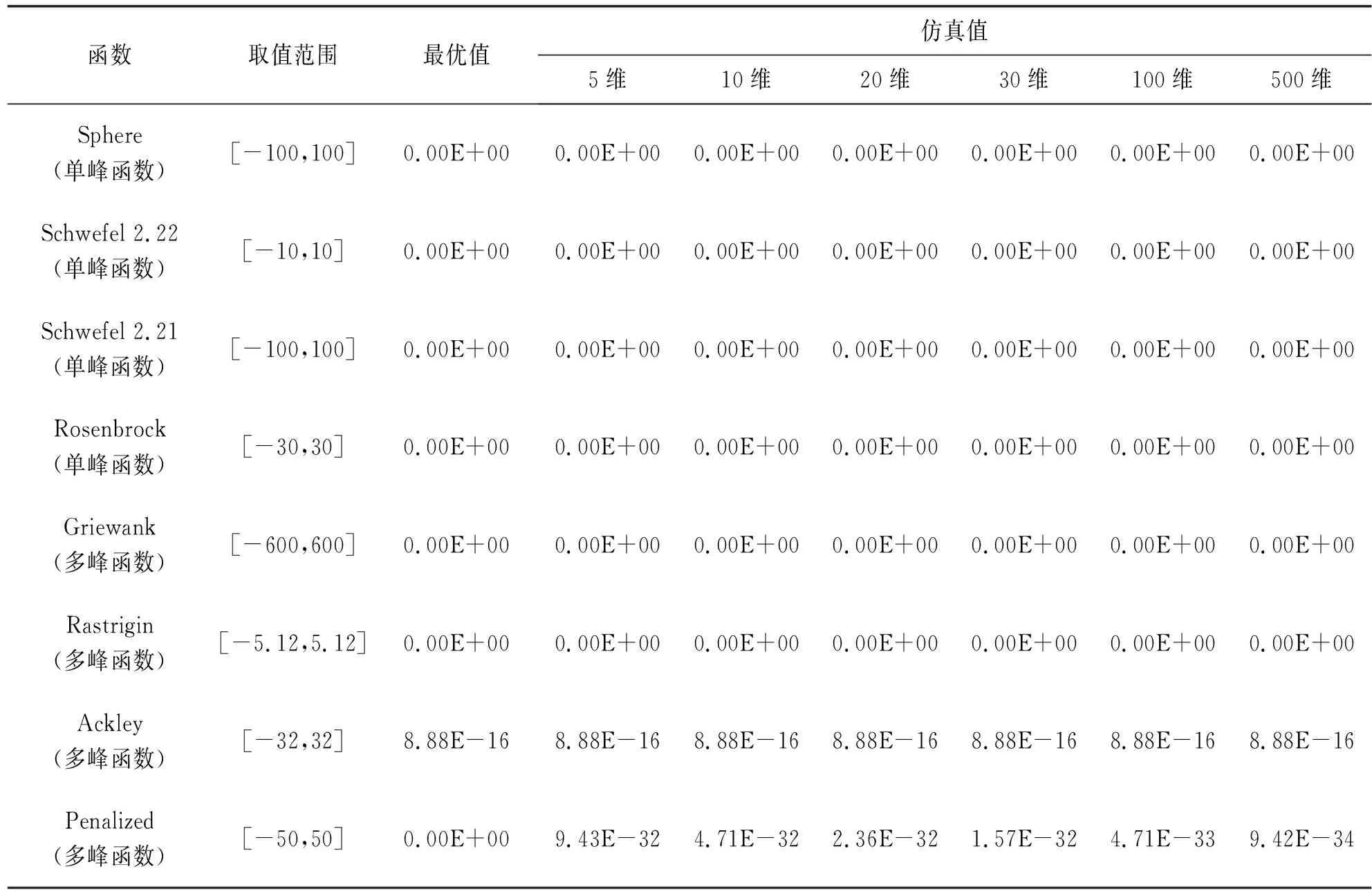
表1 FSA标准测试函数寻优结果

a)对于Sphere、Schwefel 2.22、Schwefel 2.21 3个单峰函数，FSA在不同维度条件下20次寻优均获得理论最优值0；对于极难极小化的多维病态二次函数Rosenbrock，FSA在不同维度条件下20次寻优同样获得理论最优值0。对于单峰函数，FSA表现出理想的寻优精度。

b)对于多峰函数Griewank、Rastrigin，FSA在不同维度条件下20次寻优均获得理论最优值0；对于Ackley多峰函数，FSA 20次寻优获得相对理论最优值8.88E-16；对于使用正弦函数产生大量局部极小值多峰函数Penalized，FSA在不同维度条件下20次寻优精度均在9.43E-32以上，且随着维度的增加，其寻优精度呈提高趋势。对于多峰函数，FSA具有较好的全局寻优能力。

综上，FSA在低维和高维条件下对上述8个测试函数均具有较好的寻优精度和全局寻优能力，将其用于MLR常数项和偏回归系数寻优是可靠的。

2.3 多元线性回归

多元线性回归(MLR)是指在相关变量中将一个变量视为因变量，其他一个或多个变量视为自变量，建立多个变量之间线性或非线性数学模型数量关系式并利用样本数据进行分析的统计分析方法[19,24]，关系式如下：

Q=β0+β1F1+β2F2+…+βmFm

(8)

式中Q——径流量预测值；β0——常数项；β1,…,βm——MLR偏回归系数；F1，F2，…，Fm——自变量，即第一、第二，…，第m个主成分或未经降维处理的径流预报影响因子。

2.4 预测实现步骤

步骤一利用SPSS17.0对实例原始数据进行降维处理，合理划分训练样本和预测样本，将处理后的数据作为FSA-MLR模型的样本数据进行输入训练。

步骤二采用相对误差绝对值之和作为适应度函数：

(9)

步骤三设置FSA最大迭代次数T、群体规模N等参数。利用式(3)初始化当前解，并令当前迭代次数t=1。

步骤四定义局部最优解LS和全局最优解GS；通过式(4)、(5)计算局部解和全局最优解。

步骤五利用式(6)定义新解；更新局部最优解LS和全局最优解GS。

步骤六利用式(7)更新式(3)的随机初始值，计算并保留全局最优解GS。

步骤七令t=t+1。判断当前迭代次数t是否等于最大迭代次数T，若是，输出全局最优解GS；否则重复步骤四至七。

步骤八输出全局最优解GS，GS即为待优化模型常数项及偏回归系数。将优化结果代入PCA-FSA-MLR模型对预测样本进行预测。

3 应用实例

a)数据来源及分析。利用云南省龙潭站1952—2005年实测水文资料为研究对象，分别利用实测1—10月月平均流量和实测1—11月月平均流量对同年度年径流和12月月径流进行预测。经分析，该水文站1—10月月平均流量与年径流的相关系数分别为0.455、0.441、0.333、0.486、0.497、0.519、0.616、0.822、0.782、0.798，具有较好的相关性；该水文站1—11月月平均流量与12月月径流的相关系数分别为0.189、0.192、0.220、0.463、0.245、0.180、0.348、0.596、0.511、0.680，最大相关系数仅为0.680，相关性并不十分显著。本文分别选取1—10月月平均流量和1—11月月平均流量分别作为年径流和12月月径流预报因子，1952—1991年实测数据作为训练样本，1992—2005年作为预测样本。

利用SPSS17.0软件对实例数据进行主成分分析降维处理。对于年径流和月径流预测预报因子，前5个特征值累计贡献率分别达89.063%和85.827%，根据累计贡献率大于85%的原则，故选取前5个变量代替原10、11个变量进行年径流和月径流预测。主成分分析结果及降维后的数据统计见表2、3，原始数据限于篇幅从略。

表2 年径流和月径流主成分分析结果

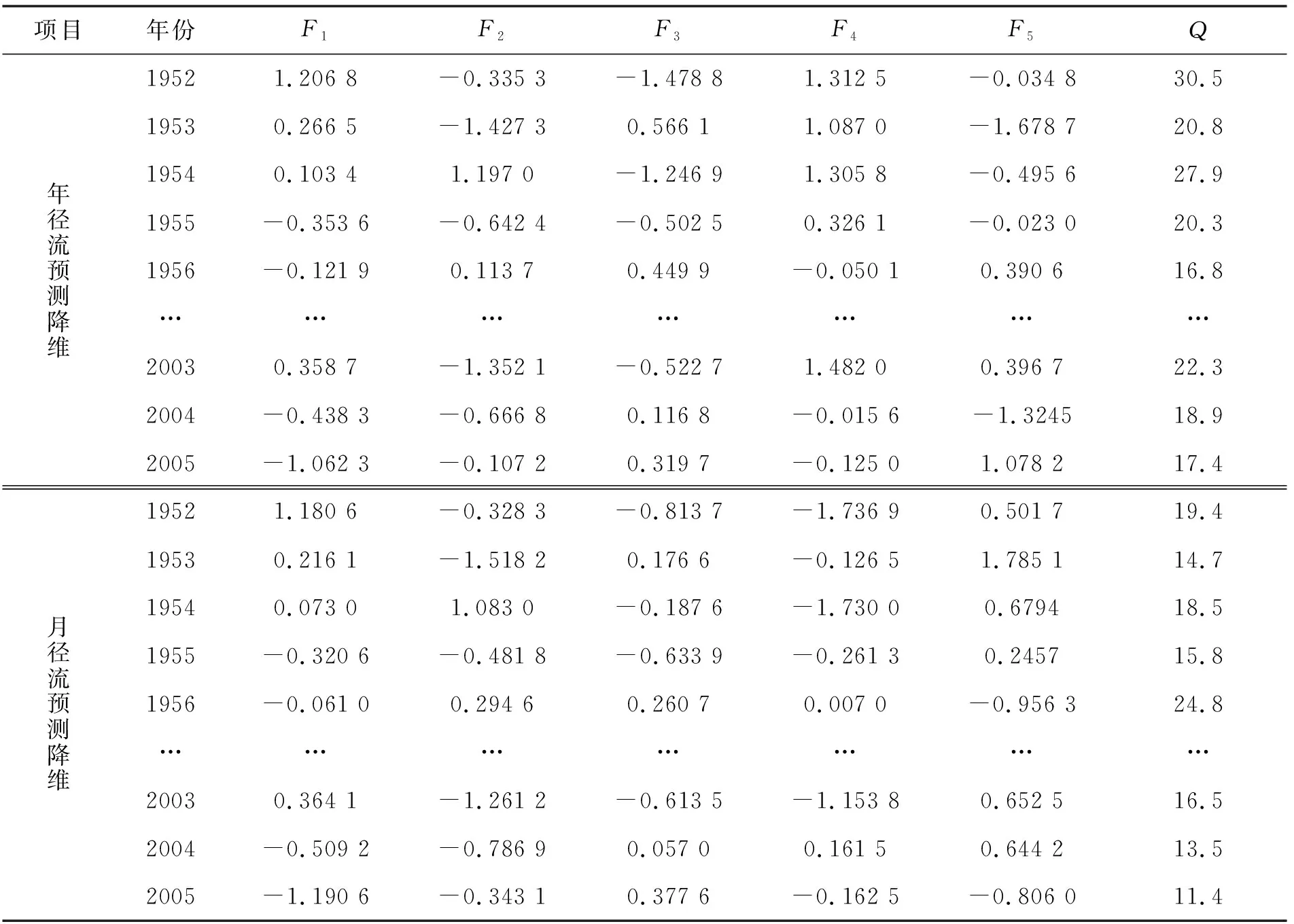
表3 年径流和月径流预测影响因子降维统计

b)参数设置。FSA参数设置同上；经PCA降维处理的MLR常数项、偏回归系数搜索范围∈[±50,±10,±5,±2,±2,±2]；未经降维处理的MLR常数项、偏回归系数搜索范围∈[-1,1]；SVM模型惩罚因子C、核函数参数g、不敏感系数ε搜索范围∈[10010-310-3;103100100]，交叉验证折数V=3，并采用[-1,1]对原始数据进行归一化处理；PCA-SVM、SVM模型最佳惩罚因子C、核函数参数g、不敏感系数ε采用试算方法获得。

c)预测及分析。建立PCA-FSA-MLR、PCA-LS-MLR、PCA-FSA-SVM、PCA-SVM、FSA-MLR、LS-MLR、FSA-SVM、SVM模型对年径流及枯水期12月月径流进行训练及预测。通过平均相对误差绝对值MRE(%)、最大相对误差MaxRE(%)、决定系数R2对上述8种模型的预测结果进行评价，结果见表4，相对误差效果见图1、2。

图1 年径流训练-预测相对误差

经FSA优化获得MLR径流与各主成分之间的最优线性回归函数关系式如下：

年径流：Q=25.5254+6.4556F1+2.9125F2-0.2639F3-0.7752F4+0.2170F5

(10)

12月径流：Q=17.2083+3.2128F1+2.3262F2-1.0993F3+0.8762F4+0.2058F5

(11)

图2 月径流训练-预测相对误差

依据表4及图1、2可以得出以下结论。

a)PCA-FSA-MLR模型对实例年径流、枯水期12月月径流预测的平均相对误差绝对值分别为1.63%、3.91%，预测精度略优于PCA-FSA-SVM、FSA-MLR模型，优于PCA-LS-MLR、FSA-SVM模型，大幅优于LS-MLR、PCA-SVM模型，远优于SVM模型，模型具有更高的预测精度和更强的泛化能力，表明PCA能对大量原始数据进行有效降维处理，FSA能有效优化MLR常数项及偏回归系数，PCA-FSA-MLR模型用于径流预测是可行和有效的。

b)从图1、2来看，PCA-FSA-MLR模型无论是拟合精度还是预测精度均优于其他模型；从预测样本决定系数和最大相对误差来看，PCA-FSA-MLR模型同样优于其他模型，表明采用多种混合策略改进的MLR模型同样具有，甚至优于SVM模型的预测精度。

c)对于同一模型，经PCA数据降维处理的模型的预测精度要优于未经降维处理的模型，说明数据降维处理可使数据样本简洁且更具代表性，能有效提高模型的预测精度和泛化能力。