n维不连续分段线性金融市场模型低周期轨道的存在性条件

顾恩国,李大洋

(中南民族大学 数学与统计学学院,武汉 430074)

越来越多的学者开始关注基于个体的金融市场模型,该模型通过突出参与者的交易活动来解释金融市场的动力学行为.该领域的开拓性贡献包括DAY and HUANG[1],KIRMAN[2]等.根据这类模型,依赖简单的交易规则,异质的有限理性投机者之间的相互作用会产生复杂的内生价格动力学行为.例如,泡沫和崩溃的出现.更多的方法可查看文献[3]. 近年来,在这一令人兴奋的领域,有几篇侧重于分段线性映射的文献[4-5].这类分段线性映射可以被看作是更复杂的非线性映射的近似.分段线性映射的优势在于它们通常允许对潜在的动力系统进行更深入的分析研究,从而提高对金融模型的动力学行为的理解. 具体例子可见文献[6-8]中资产价格的分段线性动力学模型.然而,n维金融市场模型直到现在未见相关报道.在本文中,所建立的模型代表了一个典型的投机市场,市场中图表分析师、基本面分析师和技术分析师相互作用,该模型是一个n维不连续分段线性映射.

因为最近发现分段不连续映射系统在许多领域有广泛的应用,例如:DC-DC 转换器[9], 和金融市场[10],所以用数学的方法研究不连续分段光滑映射是很重要的.在n维空间中存在一个(n-1)维流形(称为Poincaré 截面),若该流形两侧无限接近的两个点映射到相隔很远的两个点,就会产生不连续性Poincaré映射.关于一般n维不连续映射的一些与一周期和二周期轨道的存在的重要结果最近已经在文献[11]中给出.本文将根据DUTTA应用的方法对n维金融市场模型进行分析.

1 不连续的金融市场模型

在本文的模型中,假设金融市场上有三种类型的投机者.投机者的交易是由造市商进行调解的, 造市商们也会根据过剩的需求调整价格.造市商对价格对数(其中Pt为价格对数)线性调整如下:

(1)

μ为调价参数.在式(1)右侧的括号中的三项分别表示图表分析师、基本面分析师和技术分析师的交易量.显然,过度买入会推高价格,而过度卖出则会压低价格.图表分析师认为牛市和熊市可以持续.因此,将图表分析师的需求设置如下:

(2)

反应参数ca,cb,cc,cd均非负,如果价格处于牛市(熊市)图表分析师会积极买入(卖出),也就是说,如果价格的对数P高于(低于)它的基本价格的对数F,通常情况下图表分析师会买入.其中基本价格是一个常数,并且所有机构投资者、市场参与者都知道这一价格.ca和cc分别反映了一种普遍的乐观和悲观的情绪而cb和cd分别表明图表分析师根据他们感知到的价格信号进行交易的强度.

基本面分析师期望价格恢复到基本价格,因此将基本面分析师的需求设置如下:

(3)

同样,反应参数fa,fb,fc,fd均为非负的.因此,基本面分析师总是与图表分析师相反的方向进行交易.在金融产品价格高于基本价格时,他们卖出并在金融产品价格低于基本价格时买入.与图表分析师类似,基本面分析师的交易强度可能取决于市场环境:牛市中的价格偏差(资产价格与基本价格的差)可能引发比熊市中相同价格偏差更高或更低的交易强度，即fb≠fd.

技术分析师可以根据对历史价格规律(如趋势或周期)的观察,通过简单的技术进行预测.若预期当前价格高于历史价格的平均值时,他们将作出购买决定,以便在未来以更高的价格出售,以获得差额,其需求与价格上涨量成正比.相反,若当前的价格是低于以前的平均价格,他们出售金融产品,以尽量减少损失.因此,将技术分析师的需求设置为:

(4)

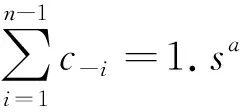
(5)

其中:

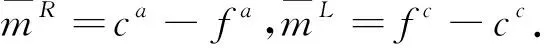
使用辅助变量xt=Pt-F得到:

(6)

其中:

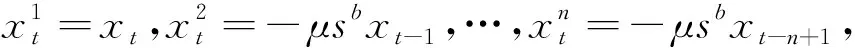
(7)

其中 ' 和T分别表示单位时间推进算子和矩阵转置,且:

i∈{L,R},

于是,该模型是一个n维不连续分段线性映射系统.

2 不动点的存在性

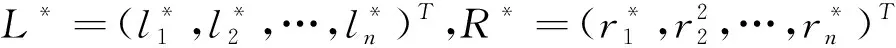
(8)

(9)

因此,假设I-AL和I-AR是可逆,可以得到:

(10)

其中Pl(1)是AL的特征多项式在1处的值.类似地有:

(11)

其中PR(1)是AR的特征多项式在1处的值.

pi(1)=-(μsb+μni)-μsbDn-1,i∈{L,R},

其中:

所以:

pi(1)=-μni,

(12)

adj(I-Ai)e1=[1,-μsb,-μsb,…，-μsb,-μsb]T,

i∈{L,R}.

(13)

将(12)和(13)代入(10)和(11)得到:

i∈{L,R}.

(14)

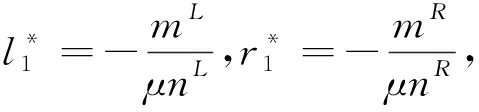
命题1

3 二周期轨道的存在性

PR=ALPL+mLe1,

(15)

PL=ARPR+mRe1.

(16)

用(16)式减去(15)式,得到:

ΔP=ARPR-ALPL+(mR-mL)e1,

(17)

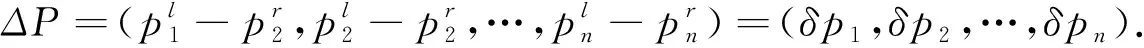
(I+AL)ΔP=[AR-AL]PR+(mR-mL)e1.

(18)

同样,在式(17)的两边加上ARPL再减去一个ARPL,得到:

(I+AR)ΔP=[AR-AL]PL+(mR-mL)e1.

(19)

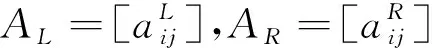
假设(I+AL)是可逆的,由(18)式可以得到:

(20)

同样,假设(I+AR)是可逆的,由(19)式可以得到:

(21)

其中:

n0=nR-nL,m0=mR-mL,

其中:

B0=adj(I+Ai)e1=[1,μsb,-μsb,…,(-1)n-1μsb,(-1)nμsb]T,i∈{L,R}.

(22)

把(20)和(21)式写成标量形式:

(23)

(24)

从(23)式和(24)式的第一个方程可以得到:

(25)

从方程(20)和(22)可以得到:

(26)

将(26)式带入(16)式,可以得到:

(27)

其中:

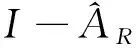
PR=αmR-βm0,

(28)

其中:

(28)式的第一个分量为:

(29)

并将(29)式代入(25),得到:

(30)

所以,有以下命题:

命题2

在映射(7)中,若满足以下两个条件:

(31)

(α1-β1)mR+β1mL>0.

(32)

则M存在一个二周期点.

4 在三维不连续分段线性金融市场模型中的应用

假设技术分析师仅关注近两个交易日的价格,即:

得到金融模型:

(33)

二周期轨道的存在条件可以从式(31)和式(32)中得到.首先要找到k1,k2的值,从第三节中知道:

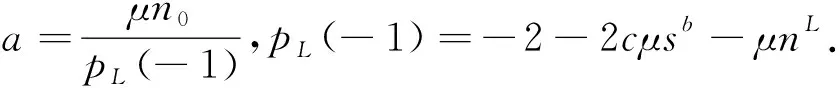
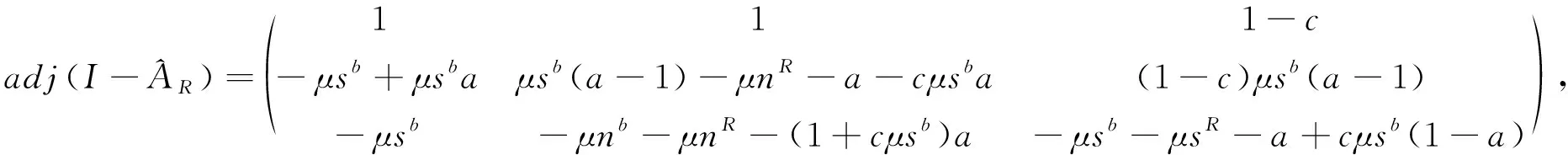
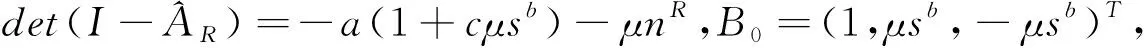
这里b=1+cμsb.利用上述等式, (31) 和 (32) 给出:

(34)

将pL(-1)=-2b-μnL,pR(-1)=-2b-μnR,n0=nR-mL代入式(34),得到二周期轨道的存在性条件:

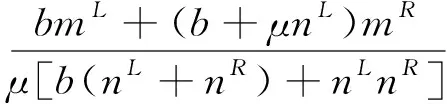
现在证明,这些确实是三维映射(33)中二周期不动点存在的条件.由于系统在边界的每一边是线性的,所以二周期(或更高周期)的周期点仅在L平面或R平面都不能存在.然而,在参数空间的一些区域中,可能存在一个二周期的周期点分别在L平面和R平面,通过求解

(35)

(36)

解上面两个方程,可以发现

这与从n维系统理论得到的结果相同.这意味着如果

nLnR>-(1+cμsb)(nL+nR).

(37)

当

(38)

则二周期轨道存在.

而且如果

nLnR<-(1+cμsb)(nL+nR).

(39)

当

(40)

则二周期轨道存在.

图1中的黑色区域给出了当参数取定μ=0.8,sb=0.5,c=0.6,nL=-2,nR=-3时，在参数平面nL-nR上的2周期存在区域，它们由条件(37)～(40)确定.

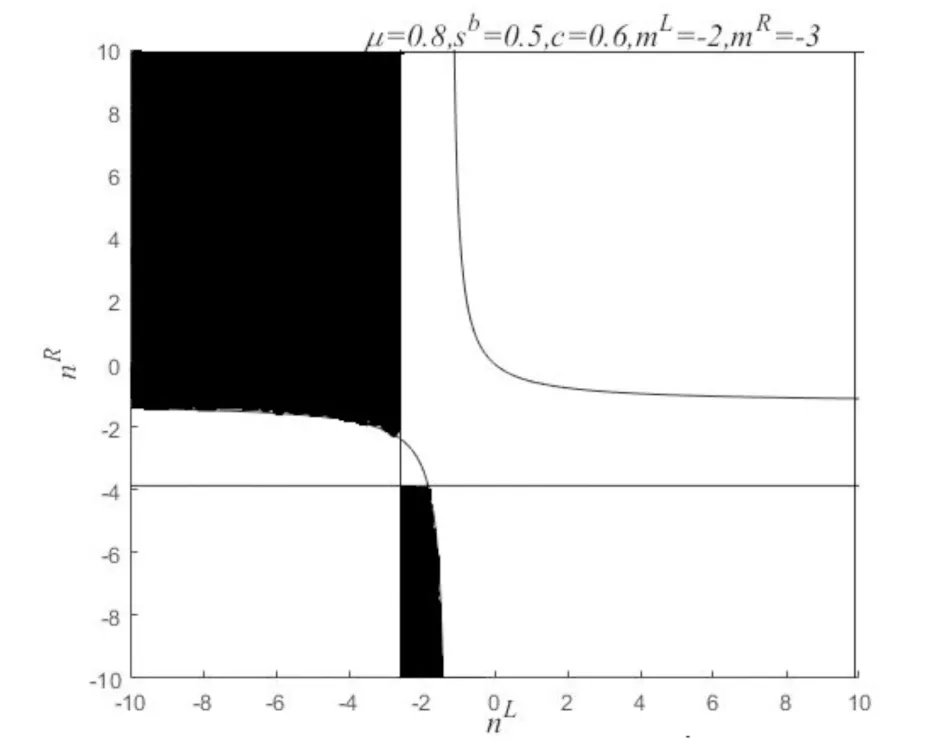
图1 nL-nR平面中2周期轨存在的区域Fig.1 The region in the plane nL-nRwhere a 2 periodic orbital exists

图2是参数设为μ=0.8,sb=0.5,c=0.6,nL=-2,nR=-3时关于两个参数(mL,mR)的分叉图,白色区域为共存吸引子存在的区域，浅灰色区域为不动点存在的区域，深灰色区域为二周期轨道存在的区域.

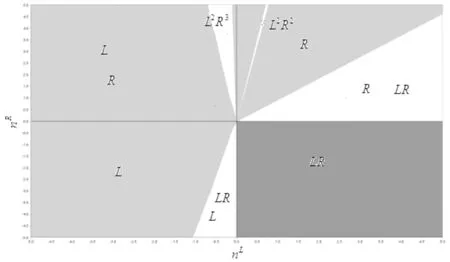
图2 关于两个参数(mL,mR)的分叉图Fig.2 Bifurcation diagram of 2-parameters (mL,mR)

5 结语

本文在TRAMONTANA 等[4-5]的基础上,建立了n维不连续金融市场模型,然后根据DUTTA应用的方法研究了该模型中低周期轨道的存在条件.最后,给出了这些方法在三维分段线性不连续金融市场模型中的实施过程. 研究发现，异质投机者间相互作用可以产生内生价格动态变化.