残差自回归模型在人工林红松树高生长规律预测中的应用1)

张毅 顾凤岐

(东北林业大学，哈尔滨，150040)

树高是森林调查中最重要的因子之一，与其它因子相比，树高测量比较困难，测量误差通常也较大。林业上比较常用的测量方法，除了直接测量法[1]之外，还经常使用模型预测法[2]进行预测，与直接测量相比，用模型预测的方式更为节省成本。现在常用的树高预测模型多是采用树高-胸径方程的混合效应模型[3-8]，是以胸径为自变量的预测树高方法。而以树龄为自变量的树高预测方法多使用传统的理论生长模型[9-12]，所以本研究以我国东北林区红松人工林为研究对象，依据实测的树高数据，将时间序列分析方法中的残差自回归模型与传统树木理论生长方程进行组合，对比组合后的模型和单独使用传统树木理论生长方程后的结果，以拟合程度和预测精度作为评判标准，选出合适的树高生长模型，可以为红松的生长状况和运营提供参考。

1 研究区概况

研究地区位于吉林省通化县三棚林场。三棚林场(125°17′～126°25′E，41°20′～42°7′N)于1958年建场，地处长白山腹地，是红松自然分布的原生地，属于北温带大陆性季风气候。冬季严寒漫长，夏季炎热短促，气温分布在-38.7～36.1 ℃，积雪厚度可达50 cm，降水量可达1 120 mm，海拔310～1 220 m。森林资源经营总面积3 198 hm2，其中林地面积为3 050 hm2，红松干果林总面积为1 119.6 hm2，森林总蓄积为28.6万m3。

2 材料与方法

2.1 试样解析

2018年10月，在通化县三棚林场中随机选取生长正常、无病虫害、不断梢的平均木1株，进行树干解析。将解析木伐倒后，按中央断面积区分方法将树干按1 m区分，在伐根处、每个区分段及1.3 m处截取解析圆盘，厚度为5 cm。每个圆盘截取完毕，立即装入塑料袋中，带回实验室。将各圆盘刨光后用扫描仪扫描后将图像输入计算机，使用数字年轮分析系统(WinDENDRO TM V6.5)测量南北东西4个垂直方向上的各圆盘年轮数和各年轮宽度。然后，采用树干解析计算程序，计算解析木的树龄(74 a)、胸径(35.1 cm)、树高(22.57 m)、树干材积(0.956 09 m3)，每个龄阶的树高生长量数据模拟见图1。

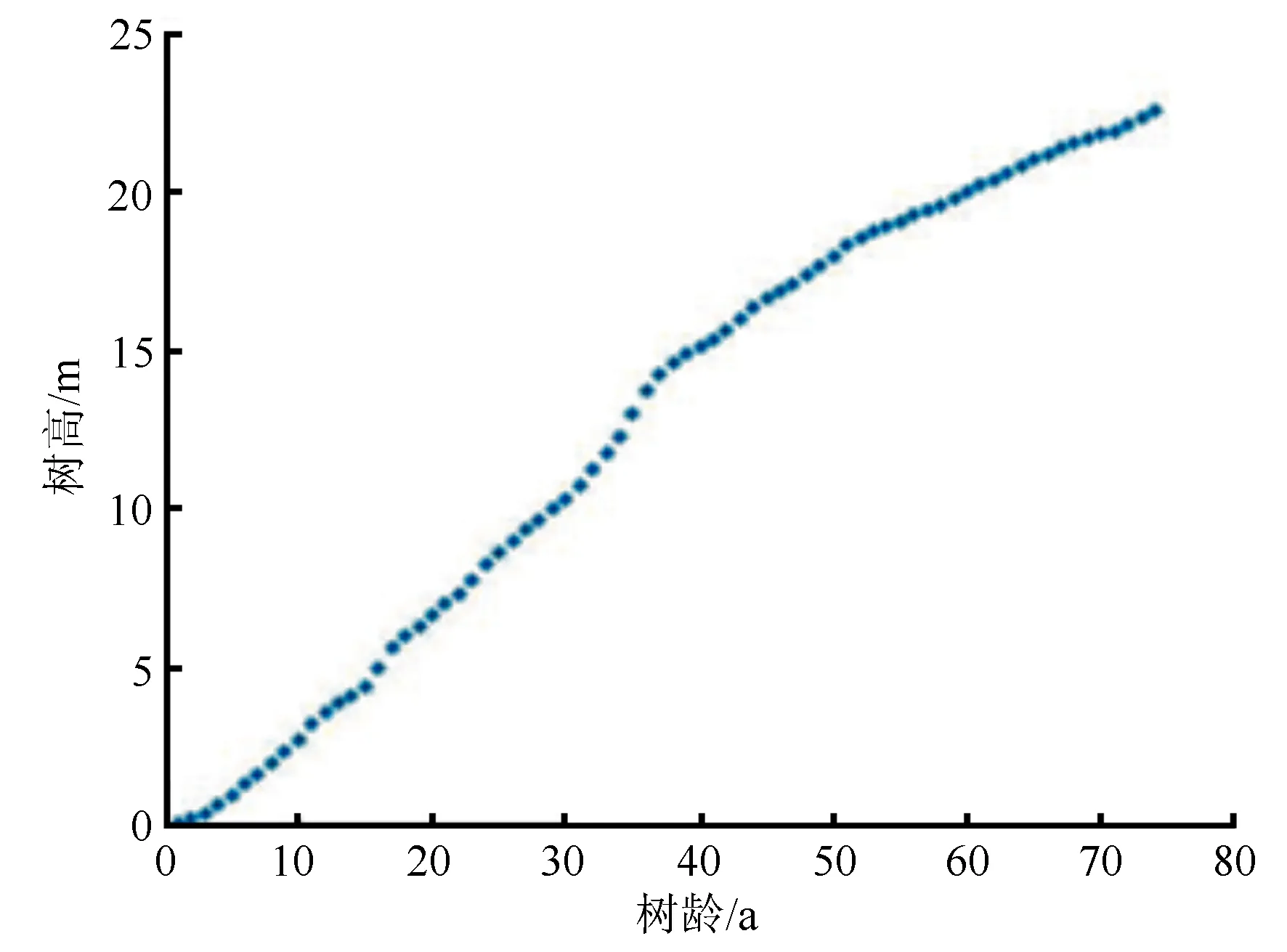
图1 树高生长与树龄关系的数据模拟

2.2 模型构建

2.2.1 传统树高理论生长模型

在树木生长模型研究中，根据生物学特性作出某种假设，建立关于树木总生长曲线的微分方程或微积分方程，求解后并代入其初始条件或边界条件，从而获得该微分方程的特解，这类生长方程叫理论方程。理论方程具有逻辑性强、适用性大、参数可独立进行检验、对未来的生长趋势进行预测等特点。在林业上，传统的一些理论生长方程，包括约翰逊-舒马赫(Johnson-Schumacher)生长方程、逻辑斯蒂(Logistic)生长方程、米切利希(Mitscherlich)生长方程、坎派兹(Gompertz)生长方程、理查德(Richards)生长方程等[13]，这些方程都可以很好地拟合树木生长趋势。所以选择这5种理论生长方程作为拟合树高数据的生长方程。

Johnson-Schumacher生长方程的一般形式为：y=Ae(-k/(t+a))，A、k、a>0。A为树木生长的最大值参数，A=ymax；k、a为方程参数，且k=1/r。

Logistic生长方程的一般形式为：y=A/(1+ce-rt)，A、c、r>0。A为树木生长的最大值参数，A=ymax；c为与初始值有关的参数；r为潜在的最大生长率。

Mitscherlich生长方程的一般形式为：y=A(1-e-rt)，A、r>0。A为树木生长的最大值参数，A=ymax；r为生长速率参数。

Gompertz生长方程的一般形式为：y=Aexp(-ce-rt)，A、c、r>0。A为树木生长的最大值参数，A=ymax；c为与初始值有关的参数；r为潜在的最大生长率。

Richards生长方程的一般形式为：y=A(1-e-rt)b，A、r、b>0。A为树木生长的最大值参数，A=ymax；r为生长速率参数；b为同化作用幂指数m有关的参数，b=1/(1-m)。

2.2.2 残差自回归模型

残差自回归模型的一般形式[14]为：yt=m(t)+ωt、ωt=α1ωt-1+α2ωt-2+…+αpωt-p+εt，t={1，2,…，T}，T为样本量；ωt为零均值平稳过程；εt为白噪声过程。第一个模型为确定性趋势模型，第二个模型为自回归(AR)模型。

残差自回归模型一般形式中的确定性趋势，实际上是数据增长的趋势，而树木生长一般呈“S”形增长，所以可以使用传统树木理论生长模型替代确定性趋势模型。生长数据一般都具备自相关性和异方差性，当对数据建模拟合时，这两种特性会干扰模型的拟合程度，降低预测精度。而自回归模型可以将数据中存在的自相关性去除，合适的自回归模型在去除数据自相关性的同时，也会削弱数据异方差性。

残差自回归模型由传统树木生长模型和自回归模型组合而成，所以同时具备两种模型的优点：既可以沿用传统理论生长方程关于树木生长的生物学性质，也可以对生长方程中未提取完的信息进行二次提取，同时去除数据自相关性和削弱异方差性，从而提高拟合程度和预测精度。

3 结果与分析

将74组数据分成拟合组和预测组，拟合组使用前71组数据建立模型并进行拟合程度比较，预测组使用后3组数据进行预测精度检验。

3.1 传统理论生长方程拟合模型

通过R软件代入拟合组数据，非线性最小二乘估计迭代参数得到5种理论生长方程参数的显著性检验(见表1)、5种树木理论生长方程的最终形式和拟合效果(见表2)。由表2可见，5种理论方程中最适合拟合数据的理论方程为Gompertz生长方程：y=23.93exp(-3.671e-0.051 19t)。

表1 5种理论生长方程参数的显著性检验

3.2 残差自回归模型

将Gompertz生长方程与原数据产生的残差使用Eviews软件建立自回归模型。①保证残差序列是平稳过程，对残差序列先进行一阶差分，再对差分后的序列进行单位根检验(扩张的迪基-福勒检验(ADF检验))，得到检验的t统计量值(见表3)。由表3可见，残差序列单位根检验值小于显著性水平在0.01下的t统计量值，认为序列是平稳的。②保证残差序列存在自相关性，对坎派兹(Gompertz)生长模型的残差进行残差Q统计量检验，比较不同滞后阶数下的残差序列自相关性，发现滞后1～10阶下的Q统计量检验显著，p<2.2×10-16。结果显示，Gompertz模型的残差序列存在自相关性，可以建立自回归模型。

从自相关图和偏自相关图(见图2)中可看出，残差序列的自相关拖尾、偏自相关拖尾，说明模型应建立自回归移动平均(ARMA)模型；综合考虑模型的赤池信息准则(AIC)值和施瓦兹准则(SC)值最小原则，建立模型(见表4)。

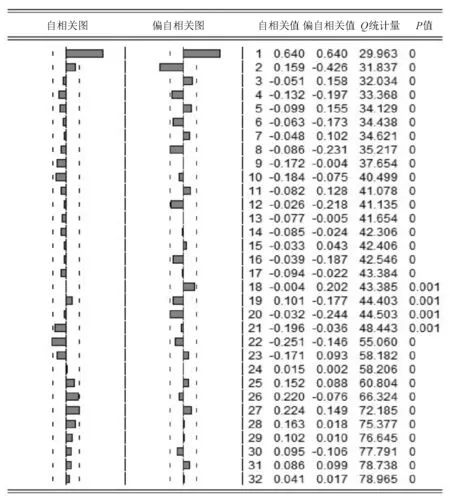
图2 树龄-树高残差自相关图和偏自相关图

表4 树龄-树高残差自相关模型结果

由表4可见，模型满足参数显著性。自回归系数多项式根的倒数为0.63、0.49和移动平均系数多项式根的倒数为0.99、0.99，均满足小于1，说明模型满足平稳可逆性。数据的纯随机性见图3，由图3可见，残差Q统计量对应的概率全部满足p>0.05，所以模型满足参数检验要求，自回归模型选用ARMA(2,(2))。检验残差序列的异方差性，使用怀特(white)检验，怀特检验的统计量nR2=1.953，对应的概率p=0.923 9，认为模型最后无异方差。

图3 树龄-树高残差Q统计量检验

在模型建立的过程中，虽然对残差建立的不是单纯的AR模型，但由于所有的ARMA(p,q)过程都可以通过在等式两端除以移动平均系数多项式得到AR(∞)过程[6]，因此综合得到最终的残差自回归模型为：

3.3 模型拟合

对上述2种模型拟合的树高数据情况进行汇总(见表5)，2种模型拟合后的数据见图4。

表5 2种模型拟合结果

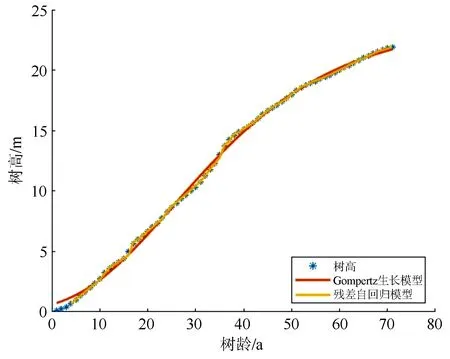
图4 树龄-树高模型拟合结果

3.4 模型预测

分别使用2种模型对预测组数据进行预测(见表6)，经计算得到2种模型的预测均方误差分别是0.186 4、0.072 1。

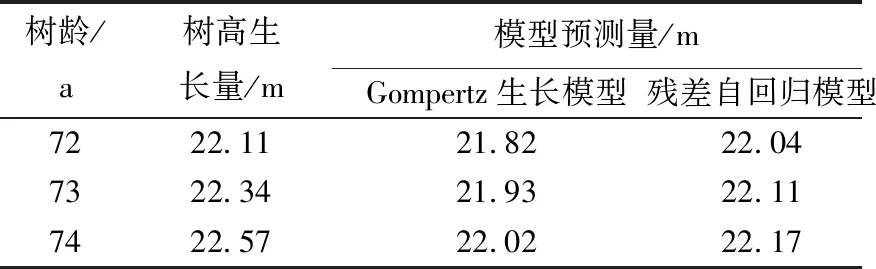
表6 2种模型预测结果

4 结论

在对树高生长数据的拟合上，Gompertz生长模型和残差自回归模型的拟合优度(R2)都很接近1，均方误差(MSE)都很接近0，但是相比之下残差自回归模型的拟合优度更高，均方误差更小，说明残差自回归模型的拟合程度更好；在对树高生长数据的预测上，残差自回归模型比Gompertz生长模型的均方误差更小，说明残差自回归模型的预测精度更高。综合模型拟合和预测结果，残差自回归模型比传统树木生长模型更适合描述人工林红松的树高生长过程。