多次短路工况下变压器内绕组辐向强度计算

邹德旭 钱国超 井永腾 王万超 张弛

（1.云南电网有限责任公司电力科学研究院 2.沈阳工业大学）

0 引言

随着电力行业的不断发展，对于电网中重要设备之一变压器受力情况的精确分析变得越发重要，其设计结构的可靠性直接影响电网的安全运行[1]。目前，一些学者已经对变压器抗短路强度问题进行了深入的研究，并且取得了许多成果[2-8]，特别是变压器绕组形变监测技术也日渐成熟[9-14]，但是对多次短路工况下变压器绕组强度的研究成果较少。

本文提出了一种多次短路工况下变压器内绕组辐向强度的数值计算方法，引入弹塑性材料特性解释多次短路冲击下绕组的力学特性。以试验变压器为研究对象建立有限元计算模型，采用电磁场-结构场耦合的方式，计算了变压器内绕组在多次短路工况下产生的辐向形变，对比分析了考虑弹塑性和弹性材料模型时，多次短路冲击下绕组形变规律。并且进一步研究了采用弹塑性材料模型时，在不同短路电流和冲击次数下绕组辐向累积形变变化规律。

1 原理分析

多次短路工况下绕组强度研究主要考虑短路电磁力载荷、绕组材料的力学特性和短路冲击次数三个方面。

图1所示为某时刻变压器绕组漏磁密分布及电磁力示意图。对于双绕组变压器而言，流过内绕组的短路电流比外绕组的短路电流大，而内、外绕组上的轴向漏磁密分布相似，因此内绕组上受到的辐向短路电磁力相对较大。并且在任意时刻，内绕组受到的辐向短路电磁力方向始终不变，因此，在多次短路工况下，内绕组的辐向短路强度会受到更加严重的考验。如图2所示，内绕组受到向内压力，外绕组受到向外拉力，内绕组电流大于外绕组电流，内绕组更易发生形变[1]。因此本文主要研究变压器内绕组辐向强度。

绕组材料的力学特性是影响绕组形变的重要因素。考虑到铜导线的弹塑性力学特性，当短路电磁力未能达到铜导线的屈服条件时，绕组处于弹性形变阶段，短路电磁力卸载后，绕组形变又会恢复。如图3的oa段所示。当短路电磁力足够大时，绕组就会发生塑性形变，即永久形变，如图3的ab段所示。当短路电磁力卸载后，绕组形变与电磁力满足胡克定律关系，曲线会沿着与oa段直线相平行的路径返回到短路电磁力零点，如图3的bc段所示。当短路电磁力为零后，导线仍存在形变量，即残余形变，如图3的oc段所示。当再次存在弹性形变时，应力应变关系如图3的cd段所示[15]。

变压器绕组短路时都会受到包括短路冲击和励磁涌流冲击在内的多次冲击。并且，对于单次短路工况，在断路器发生动作前，绕组仍遭受多个短路电流峰值的冲击。因此，多次短路工况下变压器内绕组辐向强度的研究可近似等效成多次冲击下变压器内绕组辐向强度的研究。

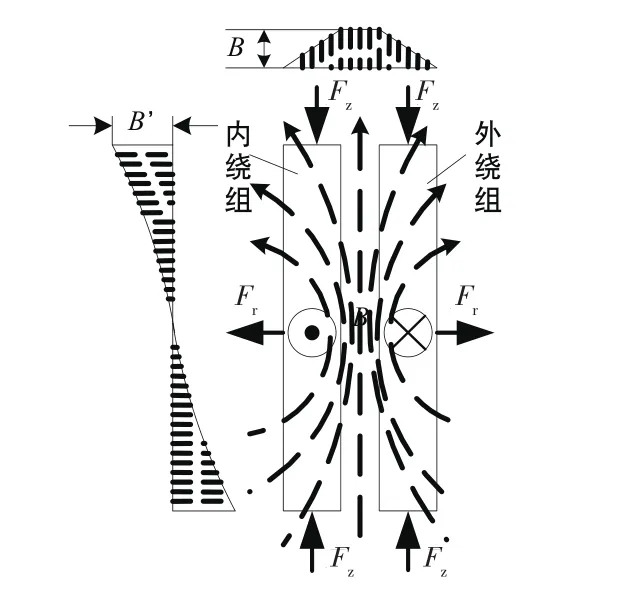
图1 某时刻绕组漏磁分布及电磁力示意图

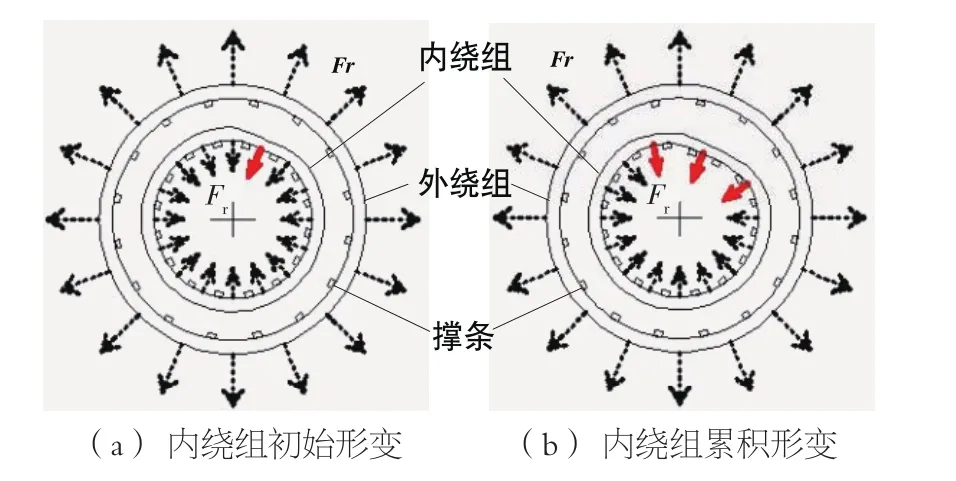
图2 累积形变示意图

图3 导线弹塑性形变曲线

2 计算方法

依留申理论[16]认为弹塑性应变是由弹性应变和塑性应变两部分组成，并且把等效应力假设成等效应变的单值函数。为了表达简明起见，这里采用指标符号。设在物体V内给定体力Fr，在应力边界Sσ上给定面力，在位移边界Su上给定位移，求物体内各点处的应力σij，应变εij，和位移ui。它们满足以下方程和边界条件：

（1）平衡方程

（2）几何关系

（3）全量本构关系

（4）边界条件

在应力边界上满足应力边界条件：

在位移边界上满足位移边界条件：

按位移求解弹塑性问题时，依留申给出了应力应变关系为：

式中，ω(εp)是与等效塑性应变有关的函数。

联立式（1）～式（6）可得：

式中，G为剪切弹性模量；K为体积模量。在弹性状态时ω=0，故上式右端为零而得到弹性解。将这个弹性解作为第一次近似解代入式（7）右端作为已知项，又可求出第二次近似解。重复以上过程，可以得到所求精度内的弹塑性解[3]。

3 有限元计算与试验验证

3.1 有限元计算方法

一般的弹塑性问题都是由变系数的偏微分方程表示，并且由于漏磁密度轴向分布不均，无法推导任意高度的辐向短路电磁力解析表达式。本文采用有限元法利用电磁场-结构场耦合的方式求解绕组的累积形变，计算方法如图4所示。通过控制给定的短路电流来模拟多次短路工况，从而计算多次短路工况下变压器绕组辐向强度。

图4 电磁-结构耦合计算流程

3.2 电磁场计算分析

本文针对一台模拟ODFPS-250000/500单相自耦电力变压器的短路试验模型进行电磁场计算分析。其中绕组按照产品大约1/6高度段数的线规和结构尺寸设计[4]。试验模型的基本参数如表1所示。忽略支撑件及匝绝缘等，建立电磁计算有限元模型如图5所示[5]。

图5 电磁计算有限元模型

表1 变压器短路试验模型参数

由于绕组漏磁通密度是随着线饼辐向距离和轴向高度变化的，因此绕组各处短路电磁力密度分布不均。图6～图7所示。由于短路实验模型没有铁心， 导致内绕组内侧的漏磁相对较大，因此，在内绕组内侧会产生与外侧相反的短路电磁力。

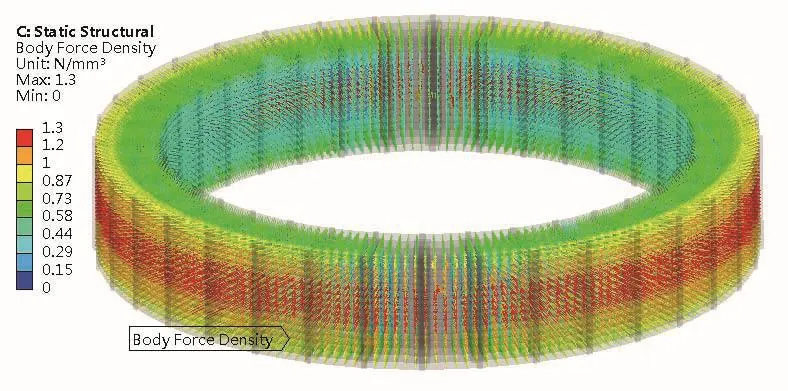
图6 电磁力密度

3.3 结构场计算分析

考虑到撑条和垫块等支撑结构件对变压器绕组结构场计算的影响，在建立有限元模型时，按照实际尺寸建立了内绕组的内外撑条和段间垫块，如图5所示。弹塑性材料模型参数如表2所示。实验测得铜导线塑性应力应变曲线如图8所示[6]。同时，为了对比分析，还对弹性材料模型进行了计算，其铜导线的应力应变关系为线性。

有限元计算满足以下假设：

1）忽略匝绝缘对绕组累积形变的影响；

2）短路电磁力的加载方式为简单加载。

在短路电流有效值为9437A的一次短路冲击下，对于弹塑性材料模型，变压器内绕组在辐向上发生的最大形变量为3.0mm，当撤去短路电磁力载荷后，即短路电流为零，采用弹塑性材料模型计算的绕组最大形变量为1.1mm，而弹性材料模型计算的形变量为0。证明利用弹塑性材料模型计算一次短路冲击时变压器内绕组辐向残余形变是可行的。

图7 辐向电磁力密度分布

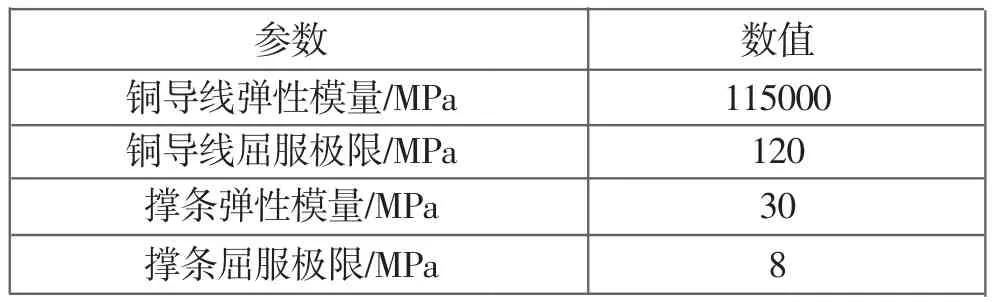
表2 仿真计算参数表

3.4 累积形变计算分析

累积形变计算涉及两个方面：一是对单次短路下残余形变的计算；二是计算多次短路工况下每次短路产生的残余形变的累积[17]。对于单次短路下残余形变的计算方法如前节所述，本节主要讨论变压器在多次短路工况下，绕组上产生累积形变的计算。

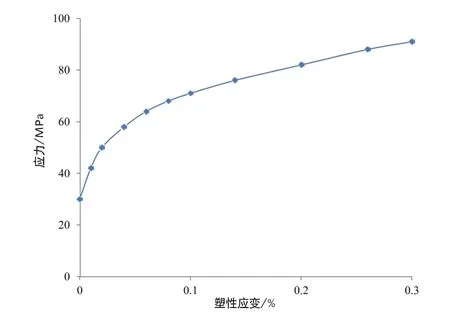
图8 铜导线塑性应力应变曲线

假设绕组遭受5次短路冲击，冲击短路电流有效值都为9437A，每次间隔时间10s[8]。由于变压器绕组模型无铁心并且每次冲击时间间隔很长，因此剩磁和温度对绕组累积形变的影响忽略不计。对于弹性材料模型来说，每次短路冲击时绕组都发生了3.0mm形变，表明绕组最大形变量没有累积，这与实际不相符。对于弹塑性材料模型来说，由于考虑了铜导线的塑性力学特性，每次短路冲击都会在上次残余形变的基础上产生新的形变，随着冲击次数的增加，绕组最大变形量逐渐增大，但并不是简单的叠加。如图10所示，第一次冲击时绕组最大形变量为3.0mm，由于铜导线的硬化，其累积速率呈减小趋势。在第5次短路冲击时，绕组最大形变量达到5.4mm[9]。如图11所示，当短路电流为4089A时，由于绕组上受到的短路电磁力还不足以使导线发生塑性形变，多次短路累积后，其最大形变量仍为0.6mm。

3.5 实测验证

激光传感器安置在内绕组的第8饼内侧，直接测量该线饼的辐向位移。加载冲击短路电流有效值依次为4089A，6737A，7415A，8408A，9437A，每次间隔时间10s，共进行5次短路冲击试验。对比如图12所示。绕组波形幅值统计如表3所示[18]。

绕组累积形变的有限元计算结果和实验数据对比如图12所示。绕组在第一次短路电流为4089A的冲击结束后，绕组残余形变为0，即绕组没有发生塑性形变。随着短路电流的增大，绕组累积形变增大，其增大规律与绕组材料的塑性应变规律相近。

表3 AI0通道测量波形幅值的变化

图10 不同模型的绕组形变

图11 不同载荷下的绕组形变

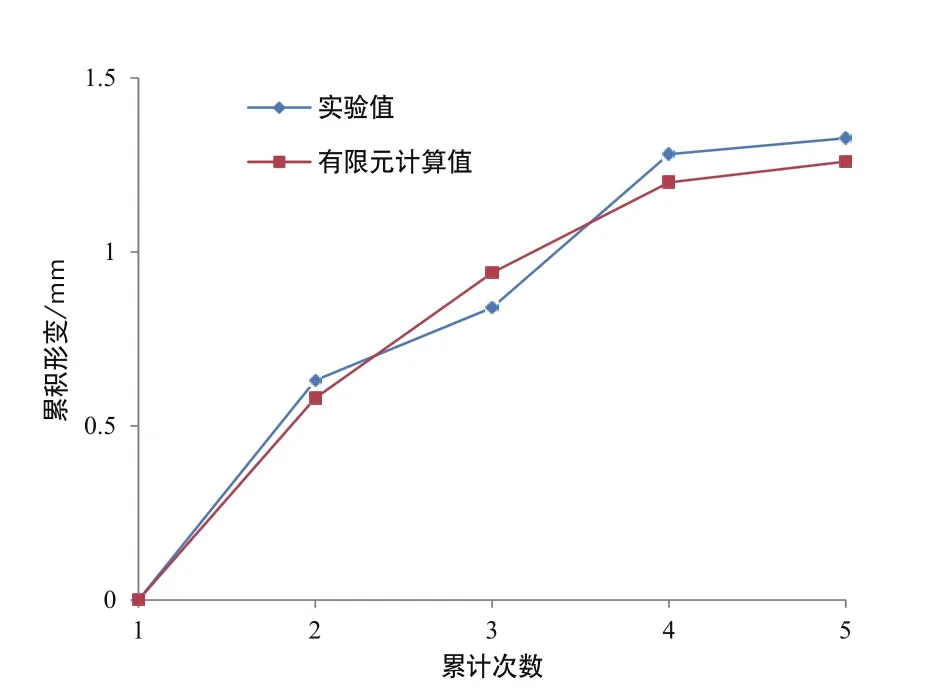
图12 实验值与计算值对比

4 结束语

本文针对变压器绕组在多次短路工况下发生辐向累积形变进行了理论分析和仿真计算，主要工作内容和结论可以归纳为以下几点：

1）通过对比计算，证明了以往文献中提出的弹性材料模型不能解决多次短路工况下变压器绕组强度问题。本文提出了利用弹塑性材料模型计算变压器绕组累积形变的方法可以有效解决多次冲击条件下变压器绕组抗短路强度问题，并且通过试验验证了该方法的可靠性。

2）计算和分析结果表明：变压器绕组在多次短路工况下产生的最大形变量与短路电流大小，冲击次数以及绕组材料特性三者的关系需分情况讨论。当短路电流较小时，绕组不产生塑性形变，冲击次数和材料特性对形变量无影响。当短路电流较大时，一次冲击下，材料特性对形变无影响；多次冲击下，弹性、弹塑性材料特性对应的计算结果有较大不同。当采用弹性材料模型时，短路次数对形变量无影响，当采用弹塑性材料模型时，形变量随冲击次数的增大而增大。

3）多次短路工况下，绕组辐向累积形变是每次短路冲击后绕组上产生的残余形变的累积。累积形变随累积次数的增大而增大，但并不是每次短路后残余形变的简单叠加。由于绕组多次短路后会进入硬化阶段，故其累积形变的增长率会减小，趋势与其塑性应变规律相近。