基于形态学滤波器与RF模型的棘波检测仿真实验

2021-06-24吴端坡王紫萌蒋铁甲刘兆霆

实验室研究与探索 2021年5期

吴端坡，王紫萌，蒋铁甲，董芳，冯维，刘兆霆

（1.杭州电子科技大学通信工程学院，杭州 310018；2.浙江大学医学院附属儿童医院，杭州 310052；3.浙大城市学院信息与电气工程学院，杭州 310015；4.浙江环玛信息科技有限公司，杭州 310052）

0 引言

随着经济的发展和社会的进步，人们对智慧医疗、智能医疗的需求日益增加，医学单一学科发展已无法满足人们的需求，随着人工智能技术、机器人技术和纳米载体技术等在医学方面的广泛应用，学科交叉与发展得到了加强，医工结合应运而生［1］。医工结合以医学为基础，以工学为手段，学科之间相互交叉与渗透，极大地推动了医疗水平发展［2］。

癫痫是大脑神经元突发性异常放电导致短暂的大脑功能障碍的一种慢性疾病，仅中国癫痫患者就有900百万人之多［3-4］。棘波是癫痫患者脑电信号（Electroencephalogram，EEG）中的典型特征波，其波形尖锐，突出于背景波，具有高幅和瞬变的特性［5-6］。Nishida等［7］首次用数学形态学的方法检测出EEG中的棘波，但没有考虑单一开-闭或者闭-开运算引发的统计偏倚现象。随机森林（Random Forest，RF）是贝尔实验室的Tin Kam Ho在1995年提出的一种机器学习算法，包含了多个决策树，其输出结果由这些决策树投票得到［8］。相对其他集成学习算法，RF具有极高的准确率，能够处理大量高维度数据，抗过拟合能力强，常用于EEG信号检测与分类研究［9］。

Matlab是矩阵运算与信号检测领域常用的数据分析平台，被科研技术人员、高校师生广泛使用［10-11］，《Matlab与仿真》是作者所在学院一直开设的专业必修课程，旨在培养学生的创新意识和规范编程的能力。本文在上述研究的基础上，根据癫痫棘波的波形特征，对脑电信号进行形态学滤波，并结合RF分类模型，通过Matlab仿真实验实现癫痫棘波自动检测，提高学生的动手能力和独立思考的能力。该实验对教学硬件要求较低，能够在高校大规模推广。

1 相关理论

1.1 数据描述与数据预处理

如图1所示，本文通过国际10-20电极分布系统采集真实病例的EEG信号［12］。该数据库中EEG信号的采样频率为1 kHz，所有数据都已经由专业医生进行了棘波放电标记。在EEG信号采集过程中，由于设备本身、肌肉活动和眨眼等因素容易产生噪声和伪迹，在本研究中采用5阶巴特沃斯带通滤波器对EEG进行预处理，滤波范围为1.6～70 Hz。

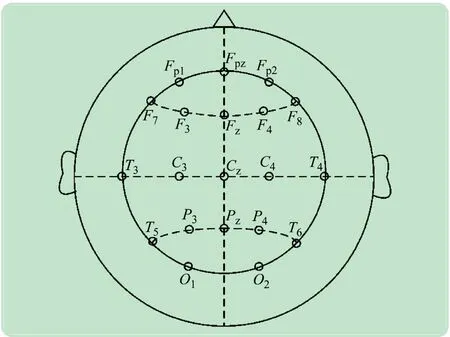
图1 国际10-20电极分布系统

本文采用了5例患者的EEG信号进行试验，分别命名为S1～S5。每个患者EEG信号的相关信息见表1。每个EEG数据中包含16个通道（Fp1、Fp2、F3、F4、F7、F8、T3、T4、T5、T6、C3、C4、P3、P4、O1和O2），本文分别使用其中能量最大的一个双极导联和平均导联EEG进行实验。图2显示了患者S1的部分癫痫棘波波形。

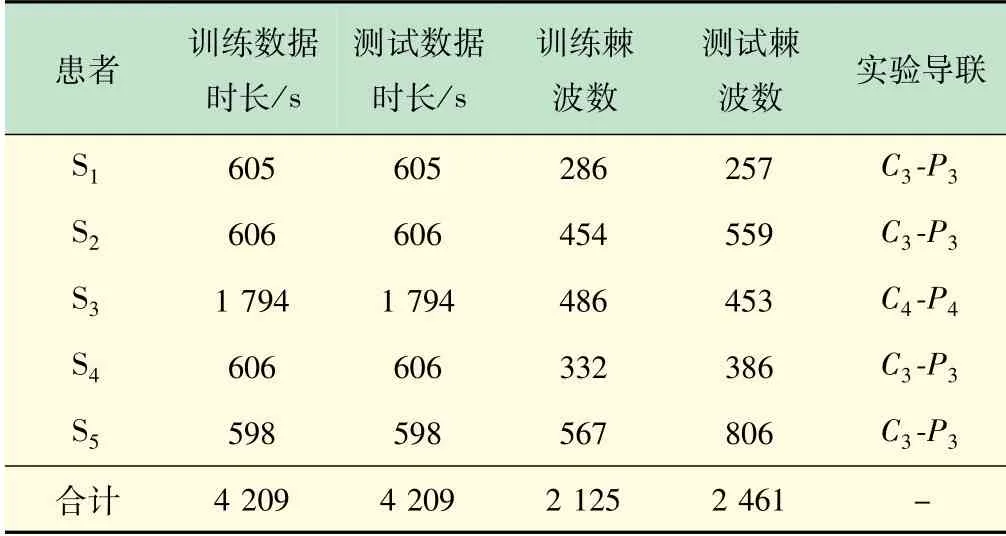
表1 训练／测试数据集的相关信息

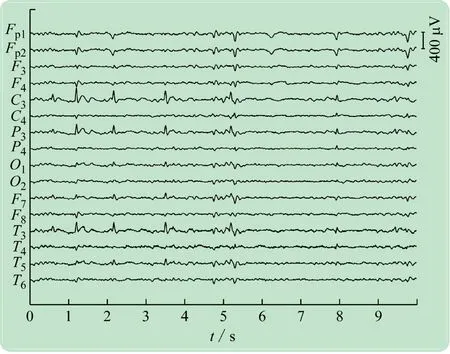
图2 癫痫棘波信号

1.2 形态学滤波器

形态学滤波器是一种非线性滤波器，它利用信号的几何特征将信号与预先设定的结构元素进行匹配，提取与结构元素相似的信号特征［13-14］。形态学滤波的基本操作包括腐蚀、膨胀、形态开运算和形态闭运算：

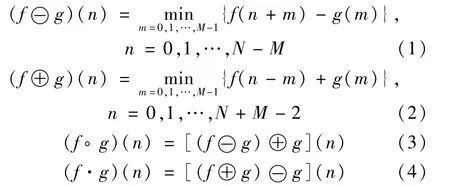
式中： f（n）为输入的时间序列；g（n）为结构元素；f（n）、g（n）的序列长度分别为N和M，并且N＞＞M；⊖、⊕、。、·分别为腐蚀、膨胀、形态学开操作和形态学闭操作。

2 癫痫棘波检测仿真实验设计

实验以Matlab为仿真平台，采用形态学滤波与RF模型的癫痫棘波检测算法，主要包括候选棘波检测、消除伪棘波、棘波形态特征提取和模型分类4部分，具体流程如图3所示。

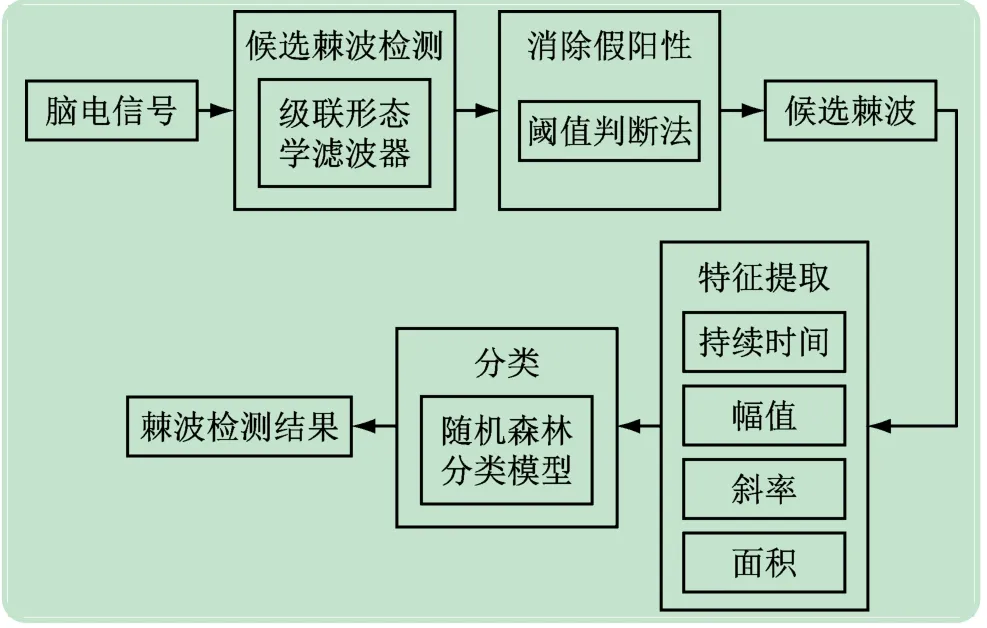
图3 癫痫棘波检测算法具体流程图

2.1 候选棘波检测

为提高癫痫棘波自动检测算法的准确性，采用形态学滤波的方法进行候选棘波检测，具体过程如下。

对单通道EEG信号进行候选检测的第1步就是选择一个合适的结构元素，选择能够最大程度反映棘波信号几何特征的三角形结构元素。三角形结构元素如图4所示，其中：A为结构元素的中心高度；2L为结构元素的宽度。

为提高棘波提取的准确率，进一步的抑制背景信号，使用了一种改良的形态学滤波方法，设置2个结构元素，根据数据集中所有数据的棘波持续时间来确定结构元素的宽度，经统计，由医生标记的癫痫棘波平均持续时间为60 ms，癫痫棘波最大波幅为结构元素高度A的范围为［130，150］。对EEG信号进行候选所用的2个结构元素表示如下：

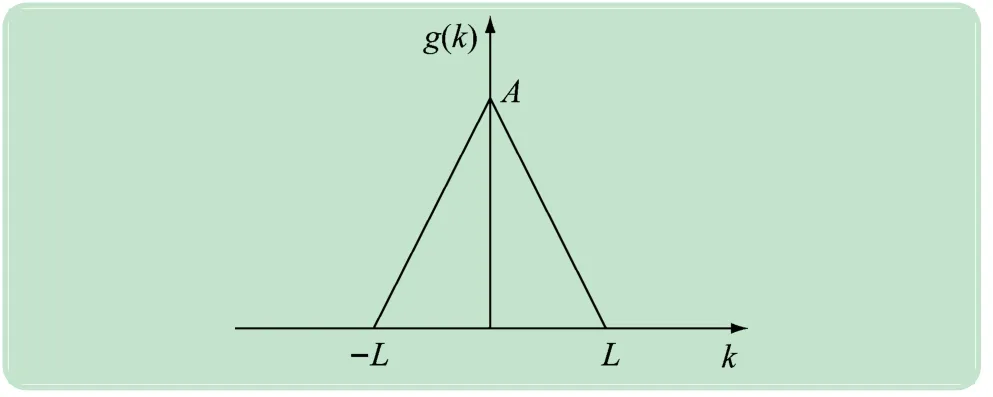
图4 三角形结构元素结构

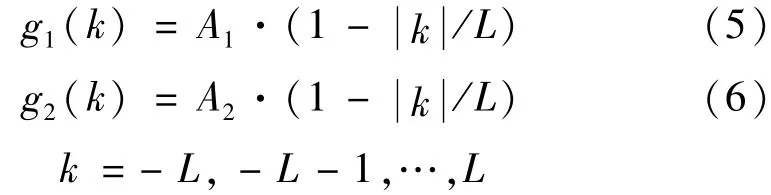
式中：A1和A2分别为130和150；2L的值为60 ms×1 kHz＝60，因此本实验中取L为30。

为同时去除信号中的正、负脉冲，消除误差偏倚，构建一个基于形态开-闭（Open-closing，OC）和形态闭-开（Close-opening，CO）级联的滤波器［15-16］：

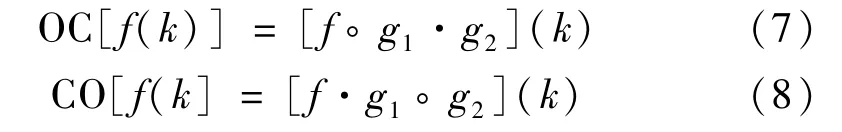
式中， f （k）为患者EEG信号。

由于开操作具有扩展性而闭操作具有反扩展性，因此单独进行OC操作或者CO操作会使结果出现统计偏倚现象。针对以上现象，使用平均加权的方法消除统计偏倚。EEG信号f（k）经过OC操作和CO操作的平均加权后，得到的输出信号即为背景信号：

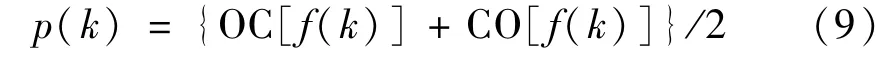
将原始EEG信号与背景信号p（k）相减得到候选棘波信号：

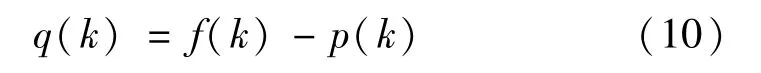
2.2 消除伪棘波

形态学滤波后得到的结果中具有很多伪棘波，对后面基于RF的棘波检测结果有很大的影响，因此使用阈值判断法消除候选棘波中的伪棘波。候选棘波EEG信号的阈值：

式中：μ为每一通道的候选棘波信号的平均值；σ为每一通道的候选棘波信号的方差。

2.3 棘波形态特征提取

消除伪棘波后，提取每个棘波10个形态学特征，以便进行模型训练和分类。这10个特征分为4类，包括持续时间、振幅、斜率和面积。持续时间特征包括：棘波左半波的持续时间Dl、棘波右半波的持续时间Dr和棘波持续时间Ds；振幅特征包括：棘波左半波的峰值Al、棘波右半波的峰值Ar和棘波峰值As；斜率特征包括：棘波左半波斜率Sl、棘波右半波斜率Sr和棘波的锐度Ss；面积特征为Areas，图5所示为特征提取的参考图。其中：Sl＝Dl/Al；Sr＝－Dr/Ar；Ss＝Sl－Sr；

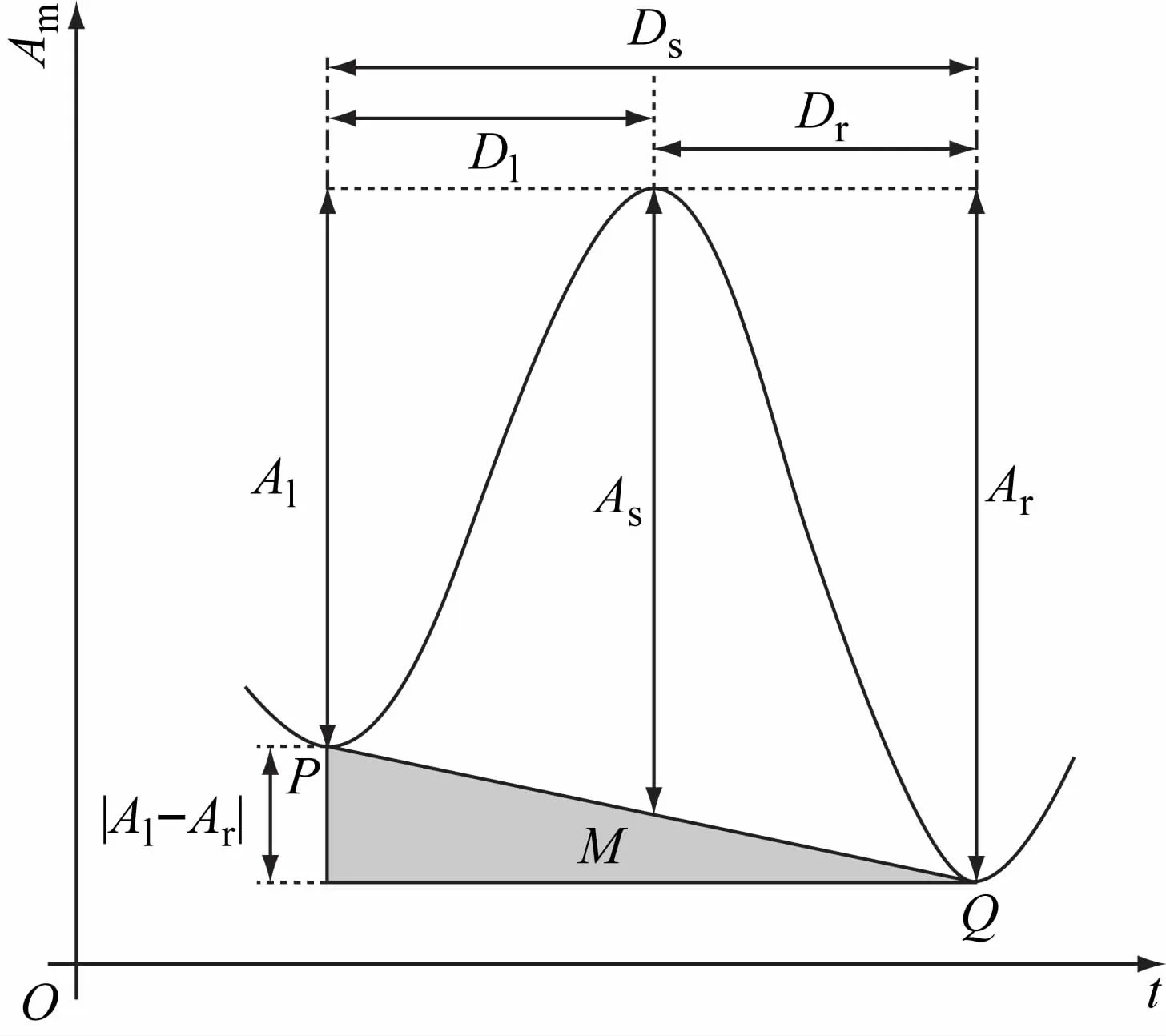
图5 特征提取参考图

2.4 随机森林分类

实验中，选择RF分类器进行棘波检测。RF中每棵树使用的数据集是随机采样的，对数据集的适应能力很强，可以减少数据不平衡的影响；对所有树的分类结果进行加权平均，得到RF分类器的最终预测结果，避免分类模型的过拟合。由Breiman提出的RF分类器包含多个决策树，其输出类别由所有树给出的最高票数决定。通过Bootstrap技术从原始训练样本集N中随机选择k个样本来生成新的训练样本集，从k个单独的决策树分类器中生成RF。RF分类器的本质是对决策树算法的改进。候选棘波的形态特征向量被输入到RF分类器中，所有可能的棘波被分为癫痫棘波和非棘波。基于RF的棘波检测流程如图6所示。实验中，将每个患者EEG信号的50%用于训练模型，剩余50%用于模型测试。

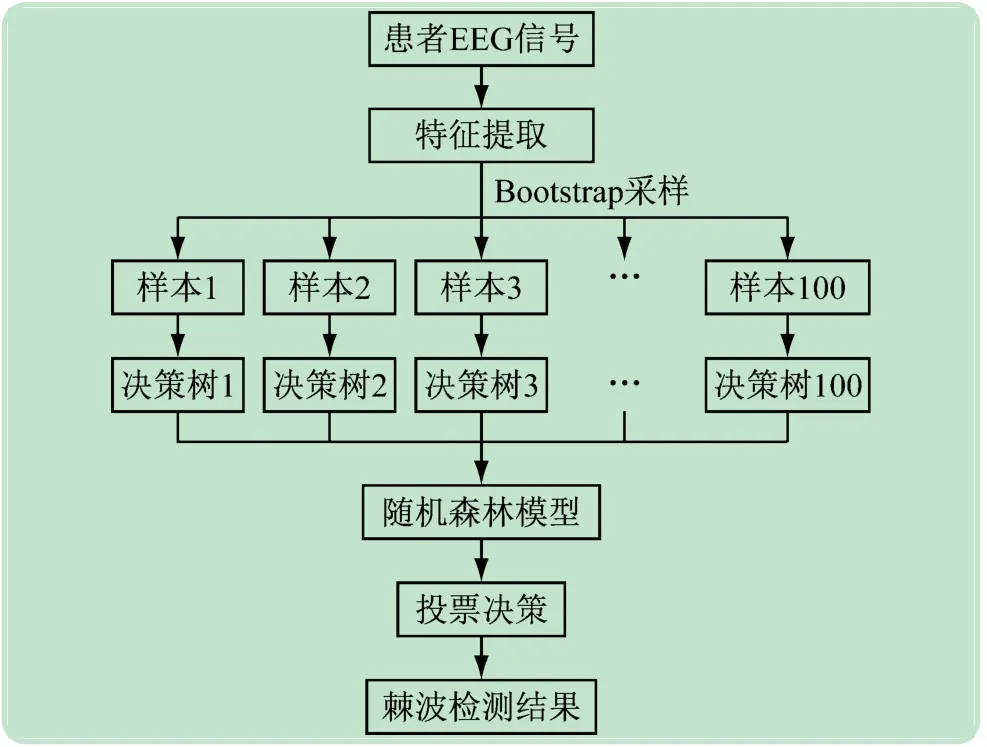
图6 基于RF的棘波检测

3 实验结果与分析

3.1 性能评估指标

为评估本实验所用方法的有效性和优越性，通过计算混淆矩阵来体现该算法得到的检测结果与专家标记结果之间的差异，混淆矩阵记为

式中：TN为检测正确的非棘波数；FN为漏检棘波数；TP为检测正确的棘波数；FP为误检棘波数。

准确性、敏感性和特异性是评估癫痫棘波检测算法性能的3个重要指标，分别记为AC、SE和SP，可由Cm计算得到，其中：AC为检测正确的样本数量与所有样本数量的比值。SE为检测正确的棘波数目与实际所有棘波数目之比，是衡量本文所提出方法对癫痫棘波的识别能力；SP为检测正确的非棘波与实际所有非棘波数目之比，是衡量分类器检验负样本的能力。

为保证仿真实验所验证的算法在实际医疗实践中具有较低的FP，采用FPM来更好地反映所提出的方法的性能。FPM每分钟的误检棘波数目：

式中：L为EEG信号记录的总持续时间。

3.2 结果分析

本实验是通过Matlab2016a软件实现的。根据不同的目的，使用表1所示的5份EEG数据进行实验。

图7所示为S1EEG数据经过形态学滤波候选检测的结果，图中t为EEG信号持续时间，Am为EEG信号的幅值。图7（a）是患者的真实EEG信号；图7（b）是经过形态学滤波后得到的背景信号；图7（c）是提取到的候选棘波信号。可见本实验使用的形态学滤波候选棘波检测方法得到的结果有较高的准确性。

为评价该仿真实验所用方法的通用性，使用AC、SP、SE和FPM对本文所提出的棘波检测方法的性能进行了评价。表2为每个患者基于单通道双极导联EEG信号的棘波检测结果。表中AC的值最小为90.7，最大为96.2。对于S1-S5的EEG数据，SE从71.8（S3）到97.2（S5），SP从93.4（S2）到97.3（S1），FP最低每分钟出现0.99个。从表3中可以看出，S3的FP远远大于其他患者，通过视觉分析，S3中未检测到的棘波的幅值与背景信号的幅值差距较小，因此易产生漏检。

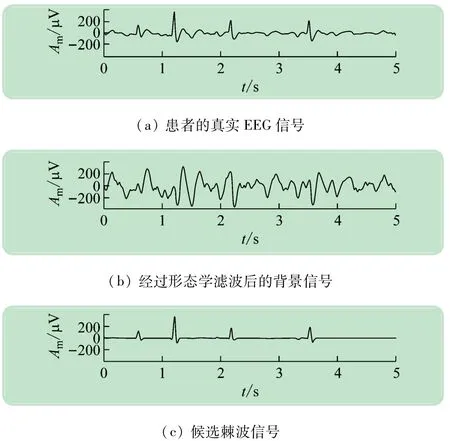
图7 形态学滤波各阶段结果

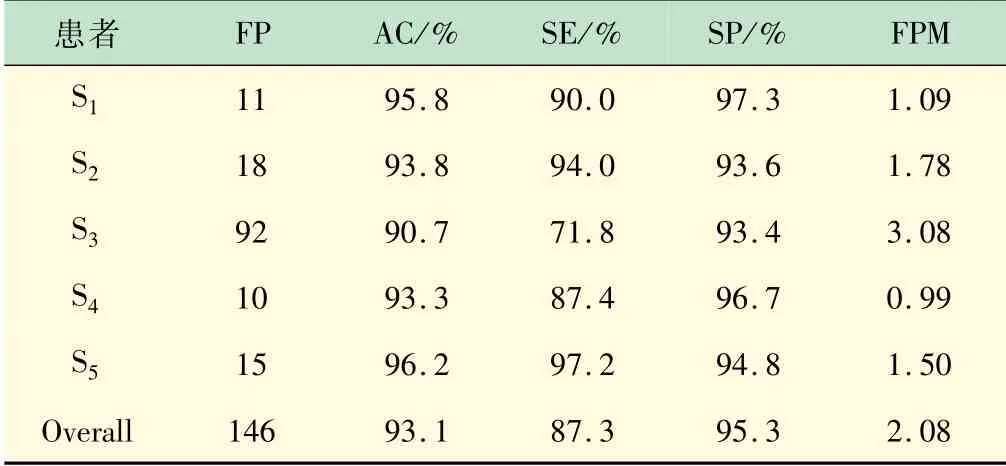
表2 基于双极导联EEG的癫痫棘波检测结果

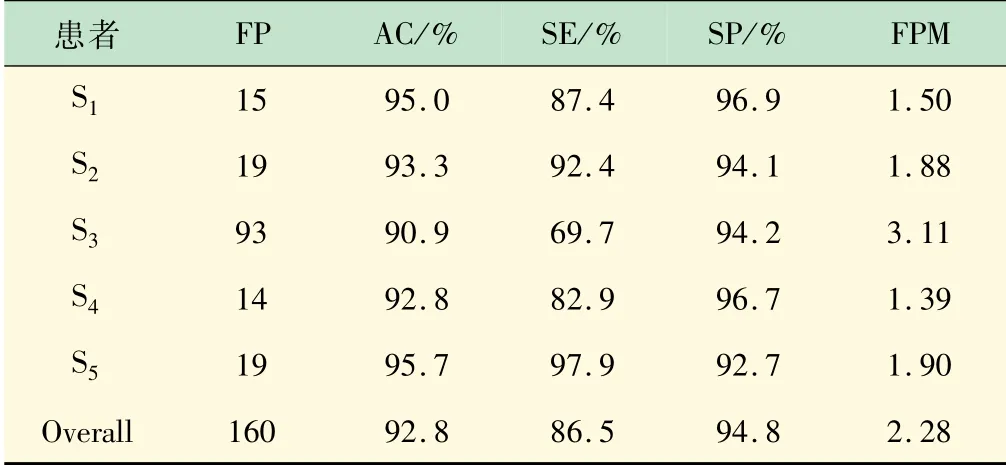
表3 基于平均导联EEG信号的检测结果

为验证本实验所用方法的可行性，表3给出了使用对应的平均导联EEG信号的棘波检测结果。比较表2、3的结果，发现使用双极导联EEG的棘波检测模型的性能优于平均导联EEG。经过分析，主要有以下2个原因：眼电图（Electrooculogram，EOG）的波形与棘波相似，双极导联EEG信号可以抵消平均导联上存在的EOG伪迹；癫痫患者的棘波放电通常出现在2个电极之间的区域，对平均导联EEG做差可以增强棘波幅值，使形态学滤波结果更加准确。

表4是本实验所用方法与其他方法性能指标的比较，所有方法均使用表1给出的5个数据进行验证。文献［17］中采用基于模板匹配的癫痫棘波检测方法，其SE低于本实验所用的方法。文献［18］中提出了一种基于人工神经网络模型的癫痫样放电检测方法，其SE仅有73.0，FPM比本实验所用方法高4.04。文献［19］中采用张量分解提取棘波特征，其性能略低于本实验所用的方法。由表4可见，文献［19］中的SE最高，为99.3，但SP仅为82.8。

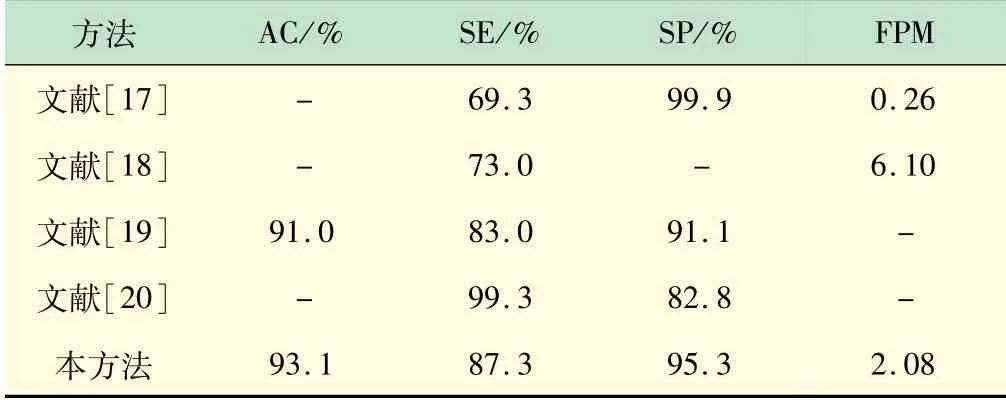
表4 本方法与其他方法的比较

文献［20］中的数据集包括健康人的EEG信号，本实验所用的数据集中仅包括癫痫患者的EEG信号，因此文献［20］中的SE会略高于其他方法。文献［17］中具有最优的SP值，但其SE只有69.3。文献［19］中的SE和SP差距较小，其性能指标低于本实验所用的方法。临床上，医生对SE的要求高于SP。因此，该方法在保证较高SE的同时，也大大提高了SP。