考虑车轮扁疤的轮轨磨耗演化及其对车线桥系统的影响分析
2021-06-24王相平丁旺才田毅吴步昊王红兵李国芳
王相平,丁旺才,田毅,吴步昊,王红兵,李国芳
(兰州交通大学 机电工程学院,甘肃 兰州 730070)
高架桥梁因不受地形限制、建造成本低、可有效防止线路沉降等优点而在高速铁路线路中得到广泛应用,但行车密度大、承受荷载高也导致其成为最易产生病害的高铁线路之一。XIN 等[1]采用概率密度演化法评估了列车−桥梁作用性能,表明桥梁上部结构变异和轨道不平顺对系统动力响应影响较大;LING 等[2]基于FE-MBD 耦合理论,分析了重载列车从箱梁桥上脱轨的动力学行为;XIAO等[3]基于概率密度演化方法,研究了车辆−轨道−桥梁时变系统的动力响应随伤损缺陷变化的随机特性;JABER等[4]分析了弹性垫层对桥梁跨中振动加速度、位移和弯矩的影响,提出了加装垫层以减小桥梁振动的方法;CHEN 等[5]计算了不同沉降幅值下车−轨−桥系统的动力响应,指出车体垂向加速度对桥墩沉降最为敏感;GOU等[6]模拟了列车运行时桥梁的动力特性,指出使用合适的设备和传感器布局可从振动响应中评估桥梁动力特性;JIN 等[7]基于Monte Carlo 可靠性分析法,提出了一种考虑车−轨−桥动力作用的综合算法,对轨道不平顺和地震作用下的车桥振动进行了模拟。轮轨磨耗作为一种轨道车辆运营过程中必然存在的现象,影响轮轨接触关系,甚至引起附加动载荷,对车线桥系统动力学性能造成严重影响。SMITIR‐UPA 等[8−9]将接触斑离散,采用半赫兹和改进的FASTSIM 算法计算了车轮磨耗分布;LUO 等[10]考虑磨耗参数的随机匹配,预测了高速列车车轮磨耗演变规律,探究了踏面磨耗对车辆动力学性能的影响;SUN 等[11]采用Kalker 变分方法研究了车轮凹磨对轨道动力性能的影响,结果表明凹磨轮对会引起轨道不均匀磨损,对车辆系统动力学性能产生较大影响;昌超等[12−13]基于非椭圆接触模型和改进的Archard 磨耗模型,研究了不同线路上的车轮磨耗演化规律。轮轨伤损缺陷引起的不平顺激励对桥梁结构服役安全产生了巨大威胁,探究外激励作用机理,揭示影响规律,提出有效的防治、监测措施已迫在眉睫。轮轨磨耗改变接触形貌,直接影响轮轨作用。实际运营过程中,轮磨和轨磨同时存在,然而当前研究主要集中在车轮磨耗上,对钢轨磨耗的研究较少,但相关研究普遍考虑了理想状态下的轮轨磨耗演化,对轮对安装偏角、初始微小踏面擦伤等非理想状态下轮轨磨耗演化极少涉及。在此,本文在考虑车线桥相互作用的基础上,采用Non-elliptical轮轨接触模型和Archard 材料磨损理论,探究了含微小扁疤车轮长期运行下的轮轨磨耗演化特征,分析了轮轨磨耗对接触特性的影响,揭示了含扁疤车轮轮轨磨耗对车辆−轨道−桥梁系统动力学性能的影响规律,为长期服役状态下轮轨伤损演化和高速铁路桥梁系统可靠性提供理论基础和技术支持。
1 计算分析模型
1.1 车线桥耦合系统
车线桥耦合系统由车辆子系统、CRTSII 型板式无砟轨道子系统和标准32 m 双线混凝土简支箱梁桥子系统组成。其中,车辆与线路依据车辆−轨道耦合理论匹配,线路与桥梁依据线桥关系耦合[14]。车辆采用CRH3型高速动车组,车轮踏面S1002CN,钢轨类型T60。轨道结构中,轨道板、支撑层采用Solid185单元模拟,CA砂浆层以弹簧−阻尼单元替代;为充分体现桥梁结构任意位置的应力应变及参振作用,同样以Solid185实体单元模拟桥梁结构。轨道、桥梁各子结构经Craig-Bamptom 模态综合法处理后组建的多体系统动力学模型中[12],轨道各层以共节点方式连接,轨道−桥梁接触关系以黏弹性力元模拟。
磨耗导致接触斑内型面曲率变化,轮轨发生非椭圆接触,故采用基于虚拟渗透的Non-elliptical轮轨接触模型[15]。该模型是一种基于“等效椭圆法”将轮轨法向接触和切向接触分开求解的方法。轮轨法向力为[15]:
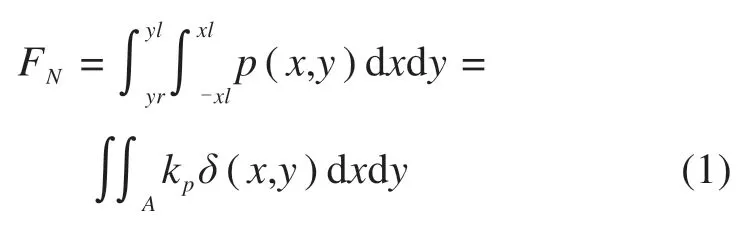
式中:p(x,y)为法向接触压力;xl,r和yl,r表示接触斑沿x 和y轴的前沿和后端;kp为比例因子;δ(x,y)为轮轨接触面上任意点(x,y)处的渗透量。蠕滑力等采用FASTSIM算法求解。
1.2 车轮踏面扁疤演化计算
圆周磨耗导致扁疤所在滚动圆半径变化,横向磨耗引起扁疤宽度改变,但由于扁疤激励主要体现在垂向,且小范围内扁疤宽度的变化对轮轨系统影响并不大[16],因此本文主要探究扁疤周向磨耗演化。
扁疤周向磨耗演化可分为新扁疤两侧棱角被磨圆演化为旧扁疤和轮轨磨耗引起的旧扁疤进一步扩展。演化过程数学模型如图1所示。

图1 扁疤演化数学模型Fig.1 Mathematical model of flat evolution
假定车轮踏面LP处出现扁疤,该处滚动圆半径R0,初始扁疤深度d0,则扁疤长度
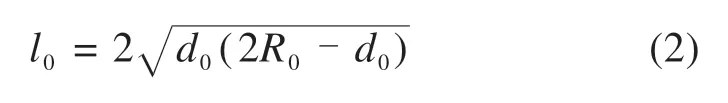
对旧扁疤,以三次抛物线f(x)模拟其两侧棱角被磨圆部分,则旧扁疤长度

若车轮周向磨耗深度Δh,则扁疤随运营里程演化的廓型函数可表示为:
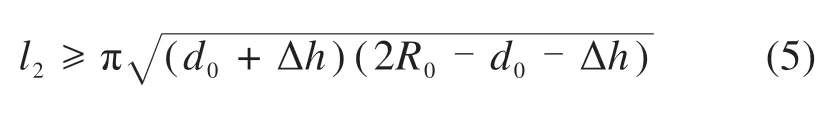
以离散点法模拟车轮踏面扁疤,如图2中扁疤模型所示,即假定扁疤在踏面Lp处,其与名义滚动圆距离为|LP|,以式(2)~(5)确定扁疤基本参数;再将扁疤长度l所在直线离散成N个等间隔的点,这些点可用坐标唯一表示,其中棱角处坐标(±xNi,f(xNi));最后将上述离散点集沿周向布置,生成踏面扁疤。小宽度范围内,可近似认为滚动圆半径未发生变化,以LP所在直线对称布置离散点,则扁疤宽度dw=2|LP|。
1.3 含扁疤车轮轮轨型面磨耗计算方法
含扁疤车轮轮轨型面磨耗计算流程如图2 所示,即基于Archard 磨耗理论进行含扁疤车轮轮轨型面更新,以1.2 节所述内容建立扁疤模型并对磨耗后的扁疤廓形进行修正,最后将修正的含扁疤车轮轮轨磨耗型面导入车线桥耦合大系统中,分析含扁疤车轮轮轨磨耗对轮轨接触特性及系统动力性能的影响。需要说明的是,由于钢轨硬度大于车轮,微小扁疤单次冲击引起钢轨伤损的可能性极小,且扁疤连续撞击钢轨同一位置的可能性也不大,故上述分析中未考虑扁疤对钢轨磨耗的影响。

图2 含扁疤车轮轮轨型面磨耗计算流程Fig.2 Calculation process of wheel and rail profile wear of wheel with flat
磨耗计算采用Archard材料磨损理论。Archard材料磨损理论是一种基于轮轨接触关系求解接触斑内磨耗深度分布的计算方法,接触斑内滑移区材料磨耗体积为
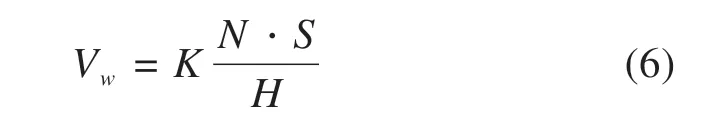
式中:K为磨耗系数;N为法向接触压力;S为相对滑移距离;H为材料硬度。磨耗系数分布如图3所示,由图3 知,踏面接触时磨耗系数为(1~10)×10−4;轮缘接触时磨耗系数取(1~40)×10−4或(300~400)×10−4,后者仅在接触压力大于0.8 倍材料硬度时选用。
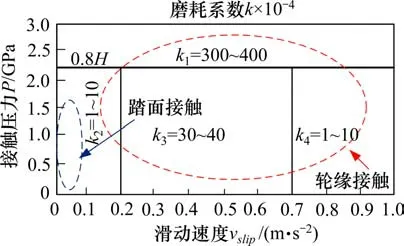
图3 磨耗系数分布Fig.3 Wear coefficient distribution
随着高速铁路技术的发展和车辆运营速度的提高,当前镟修周期的适用性尚需进一步研究[17]。选取CRH3型高速动车组轮对M2 级维护对应运行里程40万km 为研究范围,探究含扁疤车轮轮轨型面长期磨耗演化规律。不同运营里程/迭代次数下轮轨磨耗深度及廓形变化如图4所示,记相同迭代次数下对应钢轨型面为60N-0,60N-1,60N-2,60N-3和60N-4。
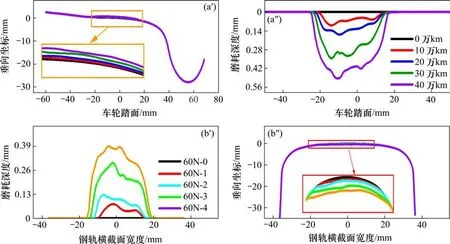
图4 不同运行里程对应轮轨型面及其磨耗分布Fig.4 Different mileage corresponds to wheel/rail profile and its wear distribution
初始扁疤深度0.05 mm,不同运营里程下扁疤尺寸变化见表1。

表1 磨耗引起的扁疤尺寸变化Table 1 Flat scar size change caused by abrasion
由表1可知,随磨耗里程增大,车轮踏面磨耗深度增大,扁疤长度增大但深度变化极小。磨耗深度增大引起扁疤长度增大而深度近乎不变,是因为扁疤磨耗以两侧棱角突出部位为主,两侧棱角的磨损导致扁疤长度扩展,而其深度变化主要受踏面磨耗影响。即初始型面含微小扁疤的车轮踏面,随运营里程增大,扁疤沿周向扩展速率大于沿径向扩展速率。
1.4 模型验证
文献[18]研究了CRH3型高速动车组在75%直线线路与25%曲线线路上运行时的车轮磨耗情况,并通过实测数据对模拟结果进行了验证。将本文模型与文献[18]进行对比,不同运营里程下一位轮对右侧车轮磨耗深度见表2。
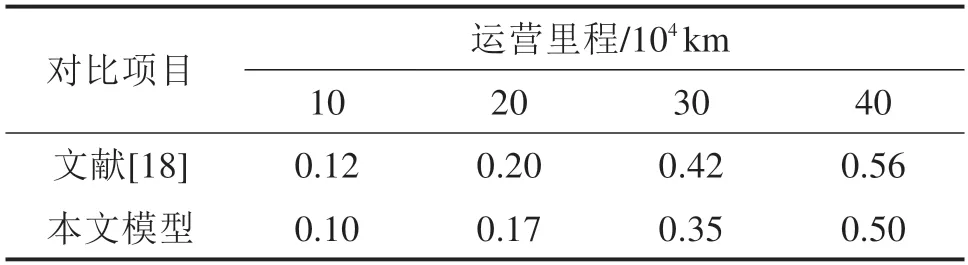
表2 磨耗深度对比Table 2 Wear depth comparison
由表2 可见,两者数值基本接近,文献[18]计算结果略大于本文模型,这是因为:1) 轨道不平顺:文献[18]不平顺幅值约为本文模型3 倍;2)线路类型:为满足高速运行条件,本文所用曲线半径普遍比文献[18]大;3)本文模型含0.05 mm 初始扁疤,初始磨耗阶段是新扁疤棱角被磨圆的过程,因此10 万km 内差别不大,但因扁疤存在一定宽度,旧扁疤磨耗并不能完全体现在名义滚动圆上,因此导致该处磨耗量偏小。
综上可见,本文模型能够较为准确地反映含扁疤车轮轮轨磨耗情况。
2 含扁疤的磨损轮轨磨耗演化对轮轨接触特性的影响
2.1 钢轨磨耗对轮轨接触特性的影响
引入接触角参数ε评估不同横移量下左右车轮接触角变化程度,接触角参数与横移量关系为[19]

以轮对横移范围内的线性函数拟合非线性接触角变化,则接触角参数

式中:S为左右车轮名义滚动圆横向跨距。
含扁疤车轮踏面与不同磨耗深度下的钢轨型面匹配时,对应轮轨接触关系(滚动圆半径差、接触角、接触角参数)的变化如图5所示。
滚动圆半径差与轮对横移量关系如图5(a)所示。由图5(a)知,全新钢轨廓形上,轮对横移量在7 mm 之内时左右车轮滚动圆半径差变化较小,最大为4.84 mm,但大于7 mm 时半径差突变至5 mm,之后随着轮对横移量的增大半径差迅速增大,轮对横移量10 mm 时滚动圆半径差约20 mm。较小的轮对横移量就会引起半径差突变,这是因为高速铁路线路钢轨磨耗普遍发生在轨头部位,轨头凹陷甚至会导致轮对横移过程中出现横向跳跃,从而加快轮缘接触进程。
轮对横移引起接触角变化如图5(b)所示。由图5(b)知,60N-0~3廓形轮对横移量小于−7 mm时接触角变化极为显著,但大于−7 mm 时变化相对较小,随着磨耗深度增加,轮对横移引起接触角变化越显著。不同轮对横移量对应接触角参数变化如图5(c),对比图5(a)和图5(c)可见,横移量在±10 mm之内时,轮对横移对应滚动圆半径差变化与接触角参数变化趋势基本一致,但超过10 mm 时,半径差增大,接触角参数反之。
2.2 含扁疤的磨损轮轨磨耗对轮轨接触特性的影响
初始踏面含微小扁疤车轮轮轨磨耗时,不同运行里程下轮轨型面匹配,其轮轨接触几何关系(滚动圆半径差、接触角、接触角参数)变化如图6所示。
图6(a)为不同轮对横移量对应左右车轮名义滚动圆半径差变化。由图6(a)知,随着轮轨磨耗深度增加,轮对横移越易引起半径差突变,但突变范围随磨耗深度增加而减小。初始型面轮对横移7 mm 会出现半径差突变,但对40 万km 运营里程的轮轨型面其横移量仅2.5 mm,与图5(a)对比可见,轮轨磨耗对接触关系的影响远大于仅钢轨磨耗对接触关系的影响。同时,磨耗深度越大,轮对横移引起半径差变化趋势也越平缓。

图5 钢轨磨耗引起轮轨接触几何关系的变化Fig.5 Change of wheel-rail contact geometry caused by rail wear
右侧车轮接触角变化如图6(b)所示。由图6(b)知,随着磨耗深度增大,轮对横移引起接触角变化幅度越大。对比图5(b)仅钢轨磨耗引起的接触角变化可见,轮轨磨耗会显著增大接触角突变时对应的轮对横移量,仅钢轨磨耗,0~40 万km 运营里程内轮对在−7~−5 mm 时接触角突变,而同时考虑轮轨磨耗时为−7~−2.5 mm。同时,仅钢轨磨耗时轮对横移量在−5~+7 mm 内不同磨耗深度对应接触角变化极小,但考虑轮轨同时磨耗时其在+4.0 mm左右出现凸起,这是因为+4.0 mm左右钢轨车轮磨耗深度同时出现极值,导致该处接触角相较于仅钢轨磨耗时有所增大。对比图5(c)和图6(c)可见,不同磨耗深度下,轮对横移引起接触角参数变化与左右车轮滚动圆半径差变化趋势相似,但同时考虑轮轨磨耗时,磨耗里程20万km 以上时其变化趋势明显增大。
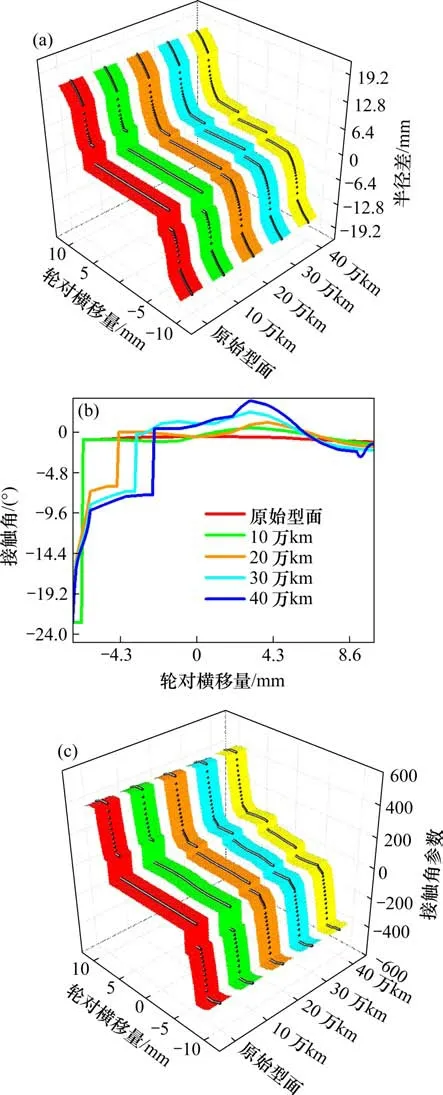
图6 轮轨磨耗引起轮轨接触几何关系的变化Fig.6 Change of wheel-rail contact geometry caused by wheel/rail wear
3 含扁疤的磨损轮轨磨耗对车线桥耦合系统动力学性能的影响
3.1 对车辆动力学性能的影响
由于考虑了扁疤的作用效果,因此相关评价指标最值受扁疤间歇性脉冲激励影响较大,故以其统计值描述。含扁疤车轮不同运营里程下轮轨磨耗引起车辆动力学性能变化如图7所示。
图7(a)为轮轨力变化曲线。由图7(a)知,随着运营里程增大,轮轨横向力总体呈增大趋势,但轮轨垂向力变化并不明显,这表明磨耗对轮轨横向作用大于垂向。对比不同磨耗里程下轮轨垂向力最大值可见,随着磨耗里程增大轮轨垂向力最大值逐渐减小。扁疤作用体现为垂向的间歇性脉冲激励,因此这个垂向力最大值实为扁疤冲击作用力,运营里程越大,垂向力最大值越小,结合扁疤形状变化可见,磨耗深度增大的同时削减了扁疤深度,导致扁疤深度变化极小而长度扩展迅速是垂向力幅值减小的主要原因。
车辆运行安全性指标如图7(b)所示。由图7(b)知,随着运营里程增大,脱轨系数和轮重减载率都呈增大趋势。不同运营里程下车辆关键部件垂向加速度变化如图7(c)所示。由图7(c)知,随着运营里程增大,构架垂向振动加速度略有增大,但车体垂向振动加速度并不明显。这是因为,磨耗引起的轮轨动力作用本身不大,经二系减振装置减振后传递给车辆的振动响应就更微弱,因此并不会影响车辆舒适性。

图7 含扁疤车轮轮轨磨耗引起的车辆动力学性能变化Fig.7 Changes in vehicle dynamics caused by wheel-rail wear of wheels with flat
3.2 对线路−桥梁系统动力学性能的影响
不同运营里程下,含扁疤车轮轮轨磨耗引起轨道−桥梁跨中垂向动位移变化的时间历程图如图8所示。
由图8知,随着运营里程增大,钢轨垂向动位移对应增大,轨道板、支撑层并未发生明显变化,且不同磨耗深度下钢轨、轨道板及支撑层垂向动位移变化趋势基本一致。钢轨垂向动位移能够直观反映不同轮对作用下钢轨变形情况;轨道板、支撑层垂向动位移时程曲线可直观反映不同转向架通过时的轨道结构垂向变形情况。不同磨耗深度下桥梁跨中垂向位移总体趋势基本一致,但局部存在明显的时间差,并非完全对应。

图8 轨道−桥梁跨中垂向动位移Fig.8 Track-bridge midspan vertical dynamic displacement
不同运行里程下,轨道−桥梁结构垂向振动加速度变化见表3。由表3可知,随着运行里程增大,轨道板、支撑层、桥梁垂向振动加速度也对应增大。对比不同磨耗深度下各结构垂向振动加速度变化情况可见,虽然桥梁跨中垂向振动加速度幅值较小,但磨耗深度变化引起的桥梁加速度变化率显著大于支撑层和轨道板,即桥梁结构对轮轨磨耗敏感程度远大于轨道结构,因此,可考虑以桥梁振动加速度间接检测轮轨磨耗状态。

表3 轨道−桥梁垂向振动加速度变化Table 3 Track-bridge vertical vibration acceleration change
4 结论
1) 扁疤车轮与磨损钢轨匹配,钢轨磨耗深度越大,轮对横移引起的滚动圆半径差、接触角变化越大,越易发生轮缘接触;含扁疤的磨损轮轨匹配,轮对横移引起的接触角、半径差变化也随磨耗深度增大而增大,且这种增大程度远比仅钢轨磨耗时的大。
2) 在扁疤车轮不发生二次擦伤情况下,随运行里程增加,扁疤长度增大深度几乎不变,对车辆−轨道−桥梁系统的冲击作用对应减弱。
3) 含扁疤的磨损轮轨,磨耗里程越大,轮轨横向力、轮重减载率和脱轨系数也越大,但轮轨垂向力变化较小,车辆平稳性几乎不变;扁疤车轮轮轨磨耗引起钢轨垂向动位移增大,但对轨道各层结构垂向动位移并无影响;桥梁结构对含扁疤的伤损轮轨磨耗演化较为敏感,建议以桥梁垂向振动加速度监测轮轨磨损状况。
