轮径差对车轮踏面磨耗和滚动接触疲劳的影响分析
2021-06-24王红兵丁旺才宋杨法李国芳吴步昊王相平
王红兵,丁旺才,宋杨法,李国芳, ,吴步昊,王相平
(1.兰州交通大学 机电工程学院,甘肃 兰州 730070;2.兰州交通大学 机电技术研究所,甘肃 兰州 730070)
随着列车运行速度的不断提高,轮轨病害对车辆运行品质的影响愈发显著。轮径差作为一种常见的车轮缺陷,不仅对车辆运行的稳定性和安全性产生一定的影响,而且会加剧车轮踏面磨耗,降低车轮服役年限。因此探究轮径差对车轮踏面磨耗和滚动接触疲劳的影响具有重要意义。国内外学者对轮径差和轮轨磨耗引起的系列问题进行了大量研究。池茂儒等[1]建立了车辆动力学模型,研究了轮径差对行车安全性的影响趋势,对比了转向架前后轮对同向轮径差与反向轮径差的影响程度。丁军君等[2]以C80型货车为例建立模型,分析了偏转角和轮径差对车轮磨耗的影响。ZOU 等[3]建立了由2 个(B0−B0)轴型机车和C80货车组成的列车模型,分析了在惯性滑行和动态制动条件下,轮径差对动轮−动轨接触关系的影响。CHENG 等[4]在SIMPACK 中建立了不同轮径的动力学模型,比较了不同轮径差下轨道车辆动态性能的仿真结果,提出了一种通过轴箱的振幅和频率来检测高速铁路车辆轮径差的新方法。陈嵘等[5−6]通过建立轮轨接触有限元计算模型和车辆−道岔耦合动力学模型,分析不同幅值和分布形式的轮径差对道岔区轮轨接触几何、轮轨法向接触性能和车辆通过道岔动力响应的影响规律,提出保证车辆通过道岔时的安全性和舒适性的轮径差限值。王璞等[7]基于Archard 材料磨损理论,建立了复杂运营条件下重载货车车轮磨耗发展的数值预测模型,通过多工况仿真并引入权重因子实现对实际复杂运营条件的模拟,进行磨耗分布计算。SUN 等[8]考虑车辆−轨道耦合动力学模型、Kalker的变分方法和谢菲尔德大学开发的材料磨损模型,建立了非均匀轨道磨损预测模型,分析空心轮对轨道磨损的影响。REN 等[9]基于考虑轨道柔性的车辆/轨道耦合动力学模型,开发了一种新的在线磨损预测模型,通过与刚性轨道进行比较,研究包括轨道柔性在内对磨损预测的影响。SHEBANI 等[10]构建了一种具有外源输入神经网络(NARXNN)的非线性自回归模型,研究了使用神经网络进行的轮轨磨损预测的准确性,并根据平均绝对百分比误差(MAPE)进行了评估。PRADHAN 等[11]在MBS 软件VI-Rail 中建立了欧洲铁路研究所(ERRI)的客车转向架模型,研究了车轮磨损和车速的变化对主动转向控制律的影响,提出了自适应转向控制律,以减缓车轮磨损。LUO 等[12]基于Archard 磨损模型和FASTSIM算法建立了非线性车辆系统动力学模型,通过考虑随机轮轨相互作用预测高速列车轮轨磨耗演变和相关的车辆动力学性能。综上所述,有关轮径差缺陷引起车轮踏面磨耗演变规律和滚动接触疲劳的研究较少。鉴于此,本文以CRH3型动车组为研究对象,应用UM 建立车辆系统动力学模型并计算全局接触参数,结合MATLAB 建立基于FAST‐SIM 算法的局部接触模型,得到接触斑内的黏着−滑移分布和切向应力分布,采用Archard 磨耗预测模型计算车轮踏面磨耗,分析存在轮径差时车轮踏面磨耗的分布变化规律。在此基础上,应用UM-RCF模块进行车轮滚动接触疲劳分析。
1 计算模型
1.1 车辆动力学模型
CRH3 型车辆动力学模型包括车体、构架、轮对和轴箱,轴箱取绕Y轴的旋转自由度,其余刚体取6 个自由度,共计50 个自由度。在动力学模型中,轮对和构架之间通过一系悬挂连接,主要是刚弹簧和一系垂向减振器,构架和车体之间通过二系悬挂连接,主要是空气弹簧、二系横向减振器,二系垂向减振器、抗蛇行减振器等。部分建模参数如表1所示。轨道部分考虑了钢轨的横向和垂向移动以及绕x轴的旋转。车轮踏面采用S1002CN,钢轨型面采用T60,轨底坡为1/40,轨距为1 435 mm,车−轨系统耦合动力学模型如图1所示。
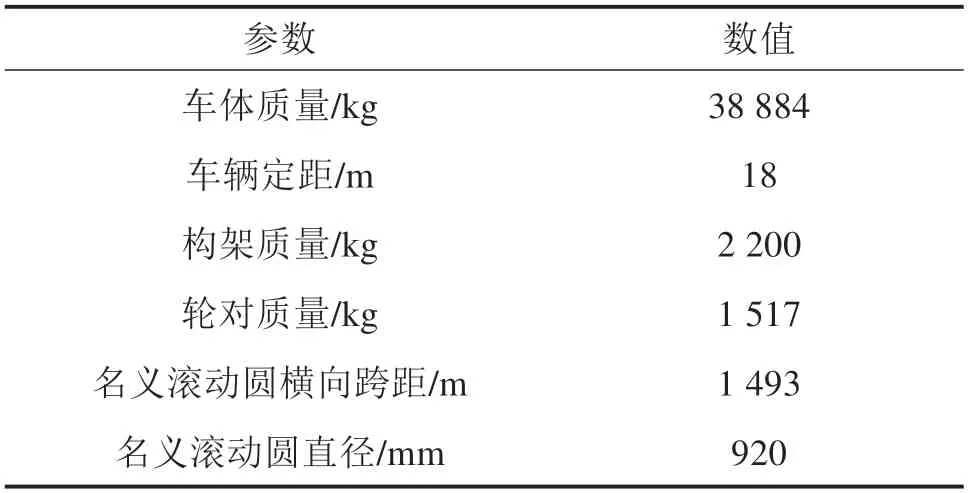
表1 模型结构参数Table 1 Model structure parameters
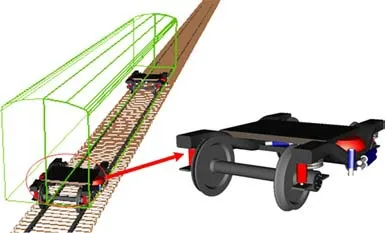
图1 车−轨系统耦合动力学模型Fig.1 Vehicle-rail system coupling dynamics model
为验证所建动力学模型的准确性,将车辆运行性能的仿真计算结果与运行在武广线上的部分试验测量结果进行对比,仿真计算采用中国高速无砟轨道谱,对比结果见表2。
由表2可知,车辆运行性能的仿真计算结果与试验测量结果接近,由于轨道不平顺的随机性,仿真结果存在略微差异,因此,本文所建立的动力学模型是可用的。

表2 计算结果对比Table 2 Comparison of calculation results
1.2 局部轮轨接触模型
尽管目前大多数动力学软件可以进行在线轮轨接触求解,但接触斑内部的应力分布及蠕滑−黏着区域的求解结果不便于进一步分析。因此,借助多体动力学软件UM 中的Kik-Piotrowiski 模型[13]进行轮轨接触计算,得到全局接触参数(等效椭圆接触斑长短轴、轮轨法向力、轮轨接触点位置等),然后输入由MATLAB 编制的局部接触模型,进行轮轨切向接触求解,得到接触斑内的轮轨接触应力分布及蠕滑速度。本文给出Kalker简化理论[14]关于切向接触的部分推导结果。
等效接触斑内每一单元的轮轨接触压应力分布为:
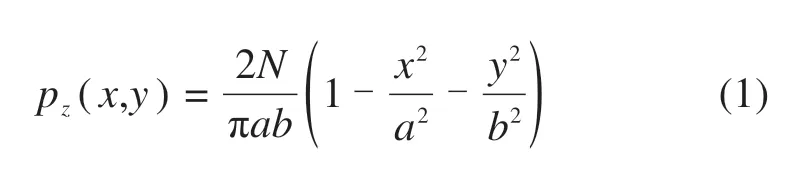
式中:N为轮轨法向力;a和b为等效椭圆接触斑的长短半轴,该参数由动力学软件输出。
假设接触斑内的弹性位移u(x,y)仅和同方向的力p(x,y)呈线性关系,即:
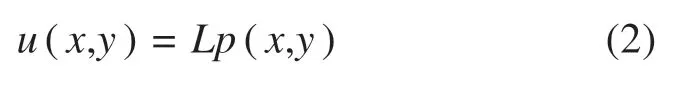
式中:L表示横向、纵向和自旋蠕滑的柔度系数。
对于每个单元节点处的切向应力由接触斑前沿向后沿差分,依次迭代求解:
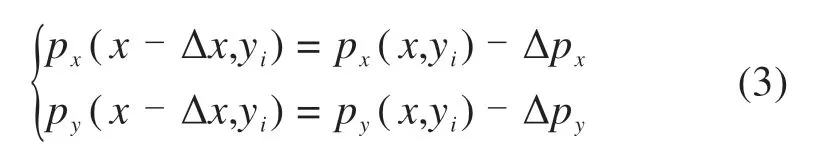
式中:Δp为相邻节点的切向应力增量。该点处的切向应力幅值为:
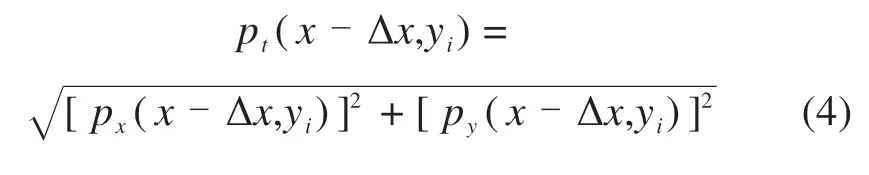
根据库伦摩擦定律,黏着−滑移区域的判断依据为:
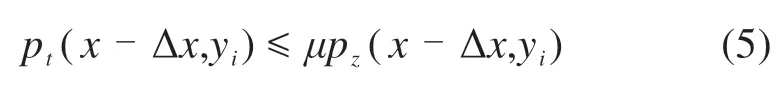
式中:μ为摩擦因数。当满足该方程,则该节点处于黏着状态;反之,则该节点处于滑动状态。对于滑动区域的节点,需要对切向应力分量进行缩减:
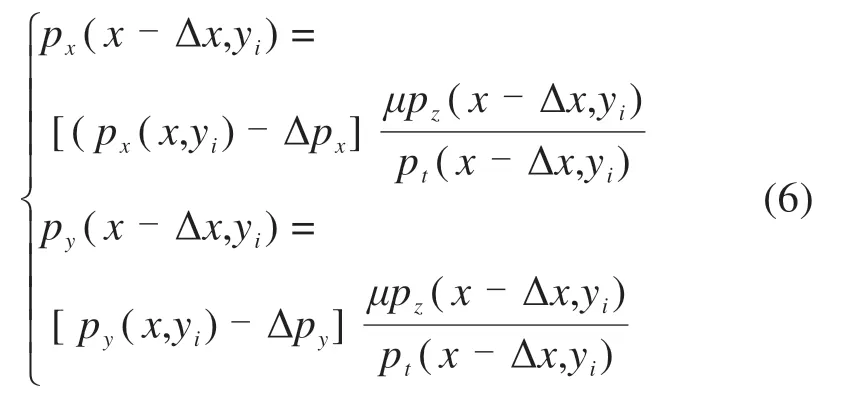
若处于黏着区,则该节点的蠕滑为0;若处于滑动区,考虑弹性变形对蠕滑的影响,滑动量的计算式如下:
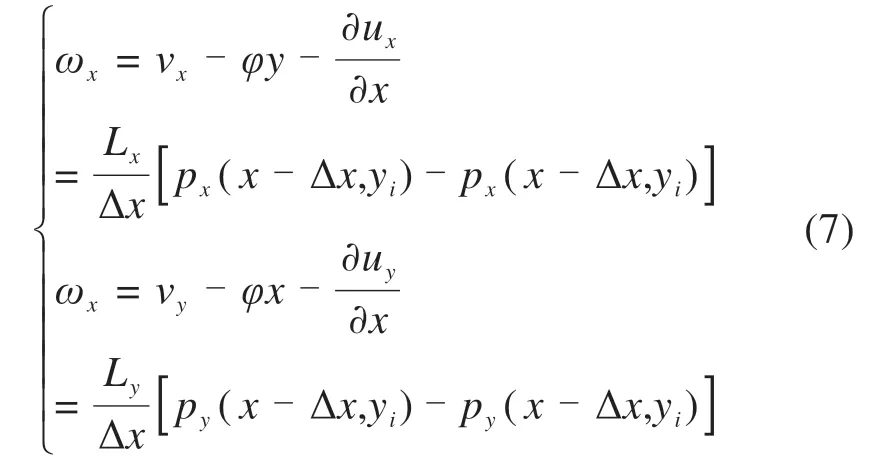
1.3 Archard磨损模型
在Archard 模型[15]中,材料的磨耗体积Vwear定义为:
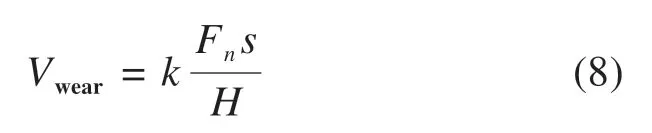
式中:Vwear为磨耗体积;k为磨耗系数,它与接触点的滑动速度和接触压力的大小有关;Fn为轮轨法向量;s为滑动距离;H为材料的硬度。
根据Archard 磨损模型,当踏面接触的情况下k大致在1×10−4~10×10−4范围内;当轮缘接触时,磨耗系数k的取值范围为1×10−4~400×10−4,如图2所示。

图2 Archard磨耗系数分布情况Fig.2 Distribution of archard wear coefficient
将轮轨局部接触模型求解结果输入Archard 磨耗模型中可计算得到接触斑内部的磨耗分布,将每个单元的磨耗量沿运行方向叠加,等效为该轮轨接触时刻的车轮踏面磨耗分布。
另外,还需要考虑车轮踏面更新策略和数据的平滑处理,根据文献[16],本文采用广泛接受的0.1 mm 踏面磨耗量作为更新的依据。且在磨耗量放大处理前和车轮踏面更新后分别采用移动平均滤波法进行一次平滑处理。
综上所述,车轮踏面磨耗的整体预测模型包含3个主要的模块:多体动力学仿真模型、轮轨局部接触模型和磨耗计算模型。整体磨耗预测模型的技术路线如图3所示。
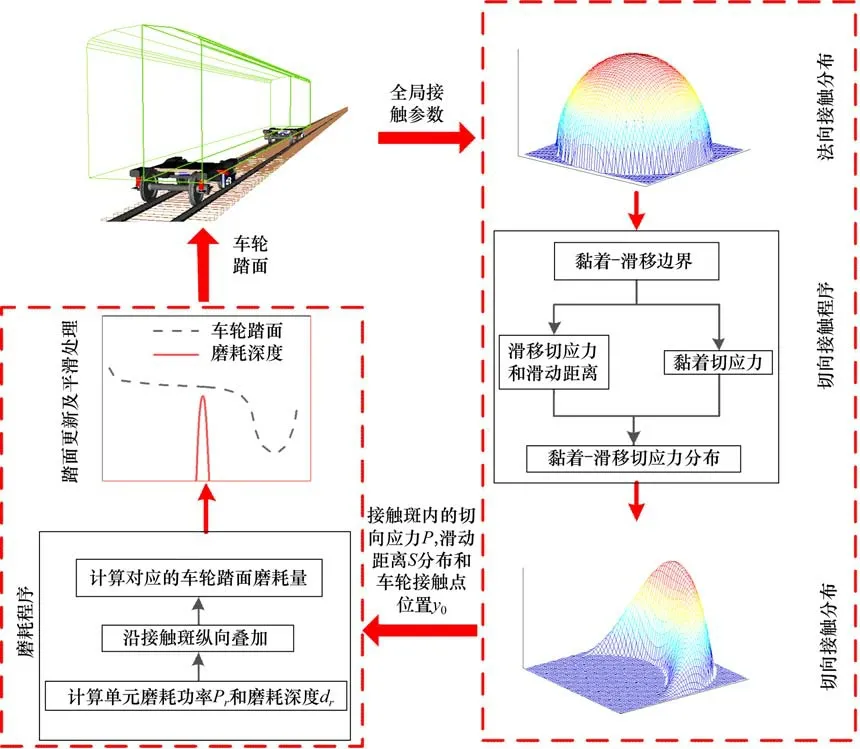
图3 整体磨耗预测模型的技术路线Fig.3 Technical route of the overall wear prediction model
2 轮径差对车轮踏面磨耗的影响
2.1 轮径差的表现形式
标准转向架4个车轮的名义滚动圆直径应完全相等,但在实际过程中由于各种因素的影响,转向架4个车轮的滚动圆直径往往不相等,即存在轮径差。轮径差的形式可能不计其数,但可以组合得到图4中转向架最典型的4种轮径差形式[1]。图4(a)的转向架前后轮对的同侧车轮直径相等,前后轮对的轮径差大小相等且正负号相同,称之为等值同向轮径差;图4(b)转向架对角线上的车轮直径相等,前后轮对的轮径差大小相等但正负号相反,称为等值反向轮径差;图4(c)只有转向架的前轮对有轮径差;图4(d)只有转向架的后轮对有轮径差。
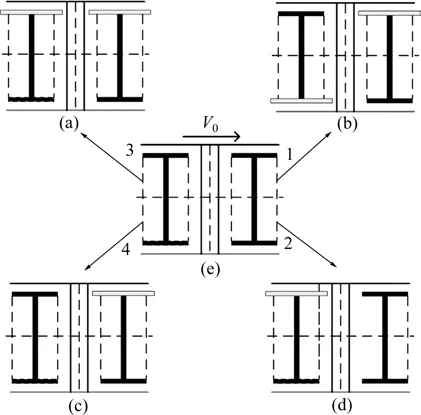
图4 4种典型轮径差的表现形式Fig.4 Expressions of four typical wheel diameter differences
为了方便统计和分析数据,依次规定车辆前转向架4个车轮的编号,即转向架沿前进方向从左至右,从前至后依次定义为1,2,3和4号车轮。
2.2 等值同向轮径差
本文以CRH3型车在直线上运行为例,运行速度为300 km/h,轨道不平顺为中国高速无砟轨道谱,分别仿真计算不同种类轮径差状态下车轮型面磨耗后廓形分布、磨耗深度和磨耗速率等。
车轮型面磨耗后的廓形分布、磨耗深度和磨耗速率随等值同向轮径差的变化情况如图5~6所示。
由图5 可知,当等值同向轮径差从的0 mm 增大到1 mm 的过程中,前转向架4 个车轮磨耗后的廓形分布和磨耗深度均越来越严重,当轮径差为0 mm 时,前转向架4 个车轮的磨耗深度最大值都为0.1 mm,当轮径差为1 mm 时,前转向架的2 号和4 号车轮磨耗深度最大值分别达到了0.38 mm 和0.32 mm,而1 号和3 号车轮磨耗深度的最大值也达到了0.23 mm 和0.27 mm,同时轮径差的存在使车轮踏面出现偏磨现象,当轮径差为0 mm 时,4个车轮的磨耗区域大致在−12~2 mm 范围内,当轮径差为0.5 mm 时,1 号、3 号车轮磨耗区域大致在−21~10 mm 和−20~10 mm 范围内,2 号、4 号车轮磨耗区域分别在−20~28 mm 和−20~25 mm范围内,当轮径差为1 mm时,1号、3号车轮磨耗区域分布范围分别为−28~12 mm 和−28~10 mm,而2 号、4 号车轮磨耗区域大致在−20~38 mm 和−18~36 mm范围内。从车轮磨耗深度分布曲线和磨耗区域分布范围可知轮径大的一侧以踏面磨耗为主,轮径小的一侧以轮缘磨耗为主。
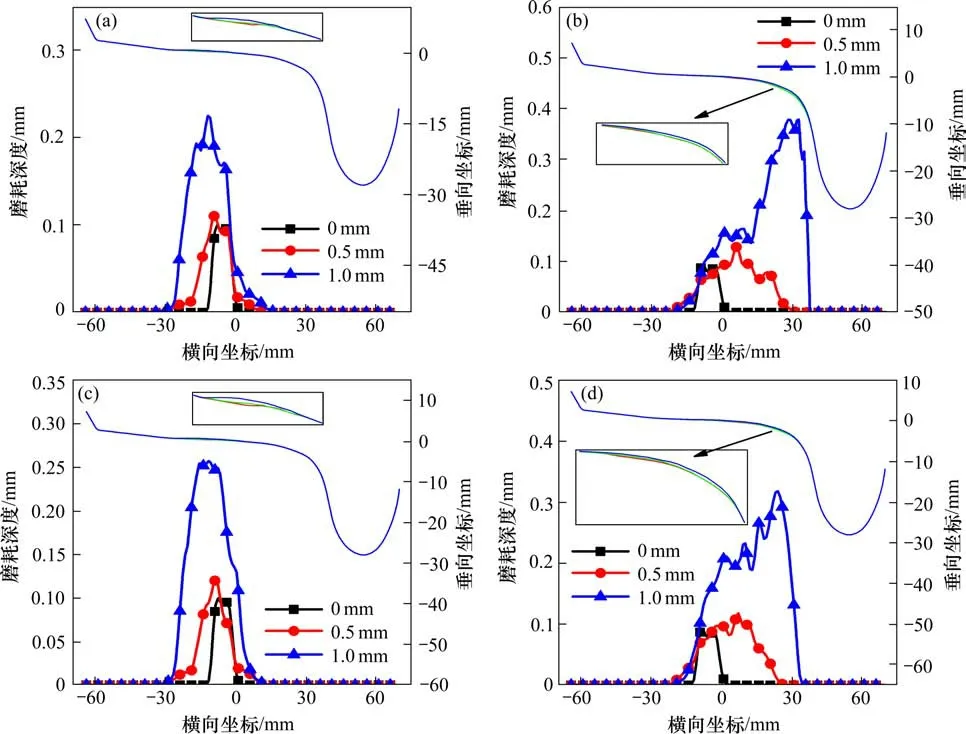
图5 等值同向轮径差对磨耗分布和深度的影响Fig.5 Effect of equivalent coaxial wheel diameter difference on wear distribution and depth
由图6可知,左右车轮磨耗速率随等值同向轮径差的增大明显增大,而且左右车轮磨耗速率的差值也变得越来越大,其中1位轮对磨耗速率的差值较2位轮对的差值更大,说明随着等值同向轮径差的增大,车轮偏磨现象越来越严重,显然2 号、4号车轮比1号、3号车轮磨耗严重。
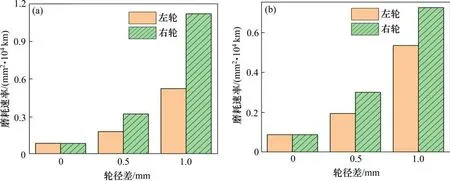
图6 等值同向轮径差对车轮磨耗速率的影响Fig.6 Effect of equivalent coaxial wheel diameter difference on wheel wear rate
2.3 等值反向轮径差
车轮型面磨耗后的廓形分布、磨耗深度和磨耗速率随等值反向轮径差的变化情况如图7~8所示。
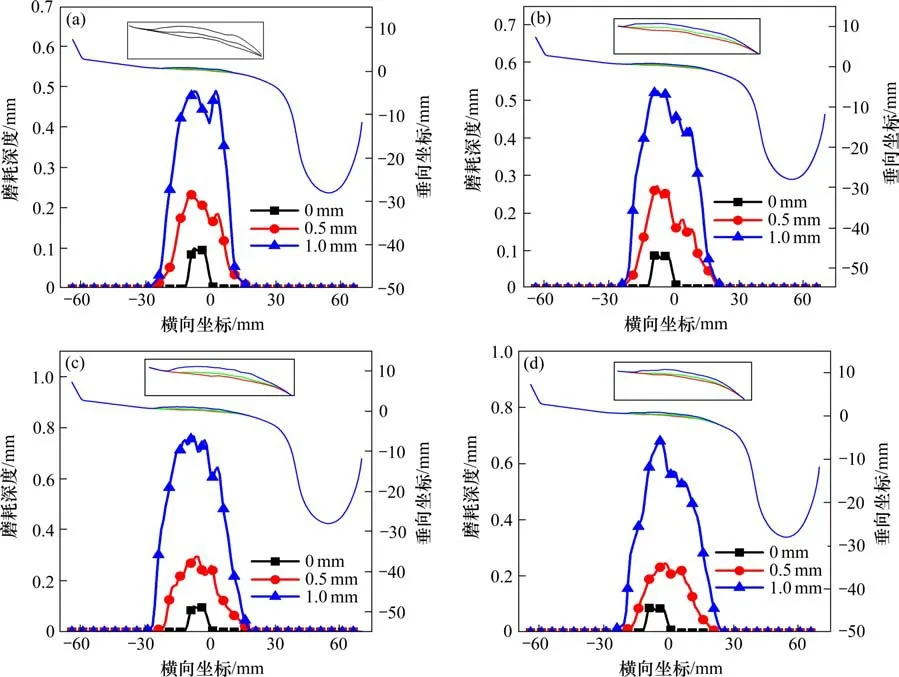
图7 等值反向轮径差对磨耗分布和深度的影响Fig.7 Effect of equivalent reverse wheel diameter difference on wear distribution and depth
由图7 可知,当等值反向轮径差从的0 mm 增大到1 mm 的过程中,前转向架4 个车轮磨耗后的廓形分布和磨耗深度均越来越严重,当轮径差为0 mm 时,4 个车轮踏面磨耗深度的最大值约为0.1 mm,当轮径差增大到1 mm 时,4个车轮磨耗深度的最大值分别达到0.49,0.53,0.78 和0.69 mm,与等值同向轮径差的情况相比较,等值反向轮径差对4个车轮的磨耗要更加严重,由于等值反向轮径差会使转向架的前轮对向右侧横移,后轮对向左侧横移,这样将导致转向架的偏转角度较大,使车辆的摇头运动也进一步增大,导致车轮踏面的磨耗区域逐渐向横向两侧方向增大。
由图8可知,轮径差从0 mm增大到1 mm时左右2个车轮磨耗速率显著增大,但是左右车轮的磨耗速率差值不大,所以轮对的偏磨现象不是很明显。
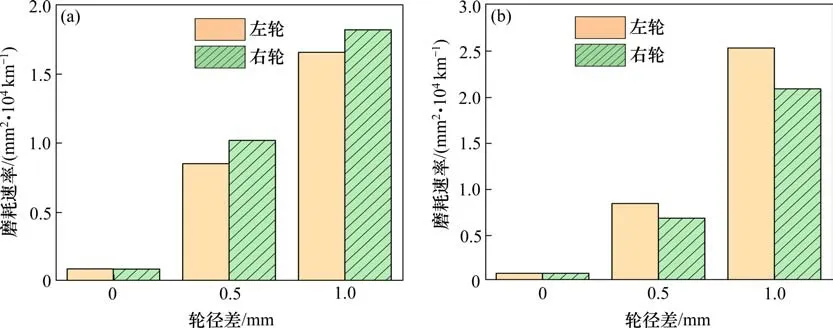
图8 等值反向轮径差对车轮磨耗速率的影响Fig.8 Effect of equivalent reverse wheel diameter difference on wheel wear rate
2.4 前轮对轮径差
车轮踏面磨耗后的廓形分布、磨耗深度和磨耗速率随前轮对轮径差的变化情况如图9~10所示。
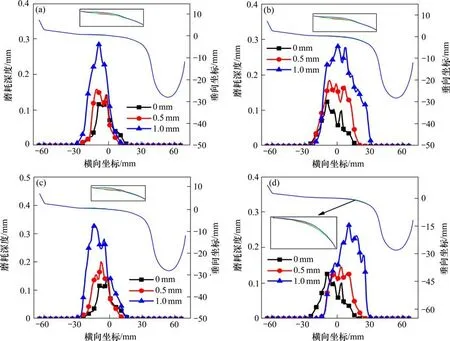
图9 前轮对轮径差对磨耗分布和深度的影响Fig.9 Influence of the difference of the front wheelset wheel diameter on the wear distribution and depth
从图9 可知,当前轮对轮径差从0 mm 逐渐增大到1 mm 时,前转向架4 个车轮磨耗后的廓形分布以及磨耗深度均越来越严重,当轮径差为0 mm时,前转向架4 个车轮的磨耗深度最大值都为0.1 mm,当轮径差为1 mm 时,2 号和4 号车轮的磨耗深度最大值分别为0.29 mm和0.27 mm,1号和3号车轮的磨耗深度最大值分别为0.29 mm 和0.34 mm。图9 中1 号车轮在轮径差为0.5 mm 时踏面磨耗区域为−26~12 mm,而当轮径差为1 mm时踏面磨耗区域大致在−30~12 mm 之间,图9 中2 号车轮在轮径差为0.5 mm 时踏面磨耗区域在−22~20 mm 范围内,而当轮径差为1 mm 时踏面磨耗区域大致在−20~32 mm 之间,磨耗区域移动比等值同向轮径差要小。
由图10 可知,同一车轴上左右车轮磨耗速率随前轮对轮径差的增大而明显变大,随前轮对轮径差的增大,左右车轮的磨耗速率差值越大,说明前轮对轮径差也会导致车轮出现偏磨现象,且2,3号车轮磨耗比1,4号严重。
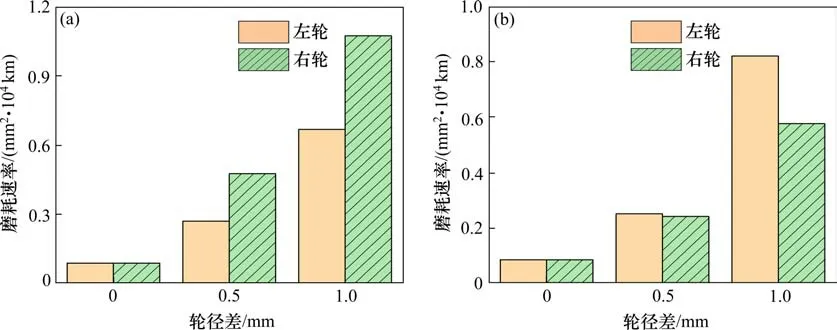
图10 前轮对轮径差对轮对磨耗速率的影响Fig.10 Influence of the difference of front wheelset diameter on the wheelset wear rate
2.5 后轮对轮径差
车轮型面磨耗后的廓形分布、磨耗深度和磨耗速率随后轮对轮径差的变化情况如图11~12所示。
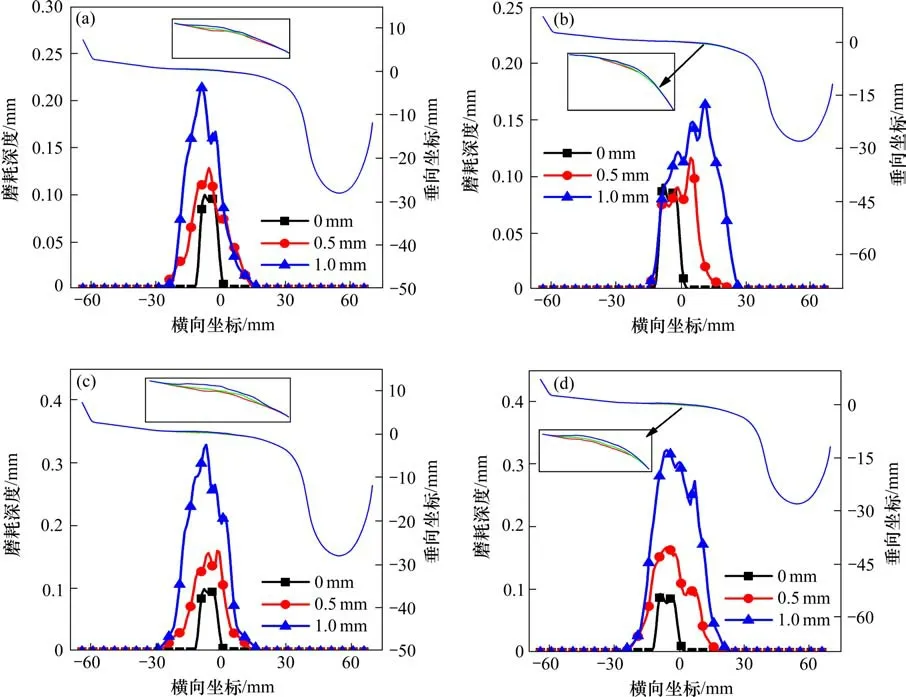
图11 后轮对轮径差对磨耗分布和深度的影响Fig.11 Influence of the difference of the rear wheelset wheel diameter on the wear distribution and depth
由图11 可知,当轮径差从0 mm 增大到1 mm时,前转向架的4个车轮的磨耗均越来越严重,同时后轮对的3 号和4 号车轮磨耗深度也比前轮对的1号和2号车轮磨耗深度大,当轮径差为1 mm时,1号和2 号踏面磨耗深度达到了0.23 mm 和0.17 mm,3号车轮和4 号车轮的踏面磨耗深度最大达到了0.33 mm 和0.32 mm。车轮踏面磨耗区域也仅有微小的移动。因此后轮对轮径差下的磨耗区域和磨耗深度均比前轮对轮径差时小。
由图12 可知,处于同一车轴上的左右两轮磨耗速率随后轮对轮径差的增大明显增大,同时左右车轮磨耗速率的差值也变大,所以说明后轮对轮径差也会导致车轮出现偏磨现象,且1,4 号车轮磨耗比2,3 号严重,但没有前轮对轮径差时严重。
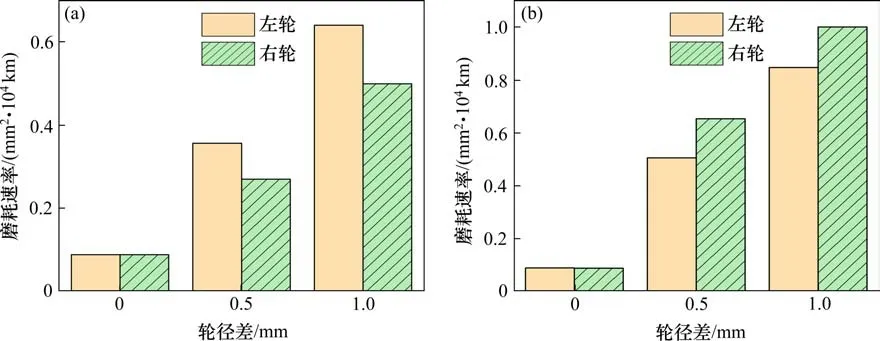
图12 后轮对轮径差对轮对磨耗速率的影响Fig.12 Effect of rear wheelset diameter difference on wheelset wear rate
3 轮径差对滚动接触疲劳的影响
车轮滚动接触疲劳是长期磨损的结果,本文应用UM−RCF 模块结合磨耗预测结果对车轮滚动接触疲劳进行分析。
由上一节轮径差对车轮踏面磨耗的影响分析对比得出,等值同向轮径差对踏面偏磨现象的影响较大,等值反向轮径差对踏面磨耗深度的影响较大,因此基于磨耗结果,分析以上2种工况下的滚动接触疲劳。等值同向轮径差工况下的滚动接触疲劳损伤和应力分布如图13所示。
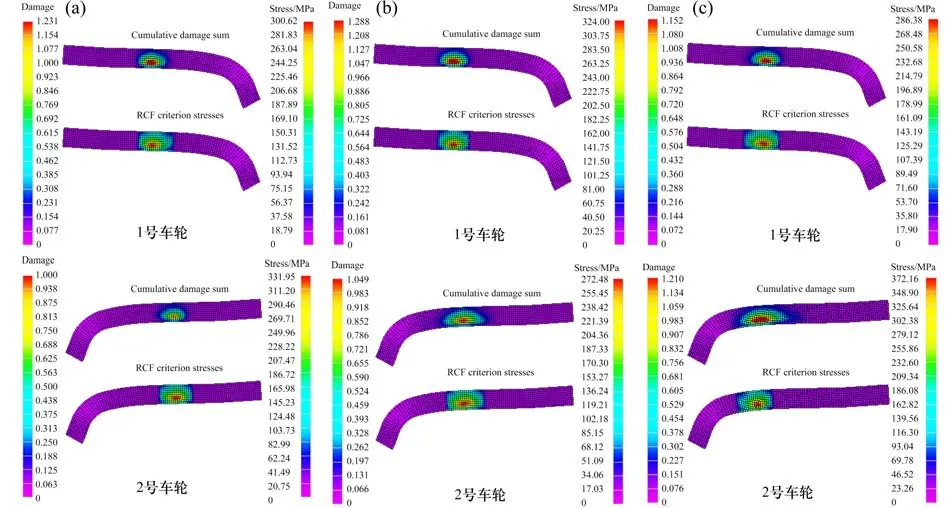
图13 等值同向轮径差对车轮滚动接触疲劳的影响Fig.13 Effect of equivalent coaxial wheel diameter difference on wheel rolling contact fatigue
由图13 可知,随等值同向轮径差的增大,前转向架左侧车轮的滚动接触疲劳损伤区域和最大应力接触点逐渐背向轮缘移动,右侧车轮的滚动接触疲劳损伤区域和最大应力接触点逐渐靠向轮缘移动,且疲劳损伤区域也逐渐扩大。这是由于左侧车轮轮径增大,导致轮对向右侧移动,故左侧车轮接触点背向轮缘方向,右侧车轮接触点靠向轮缘方向,同时导致轮对的横移量显著增大。
等值反向轮径差工况下的滚动接触疲劳损伤和应力分布如图14所示。
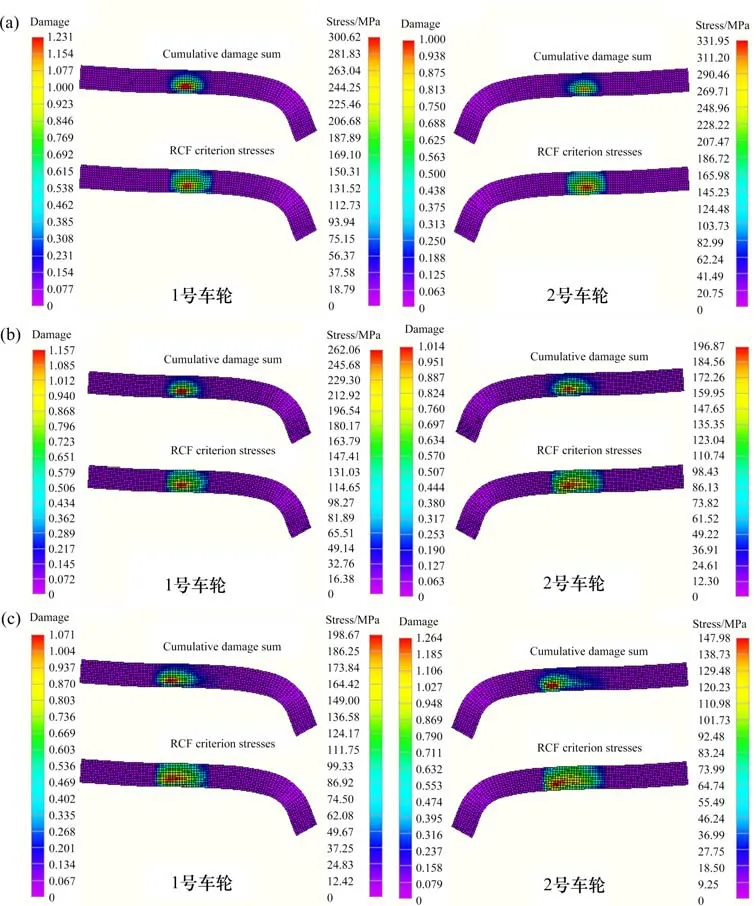
图14 等值反向轮径差对车轮滚动接触疲劳的影响Fig.14 Effect of equivalent reverse wheel diameter difference on wheel rolling contact fatigue
由图14 可知,随等值反向轮径差的增大,前转向架左右2个车轮的滚动接触疲劳损伤区域没有明显移动,但疲劳损伤区域明显向两侧扩展,由此说明等值反向轮径差不会导致严重的轮对偏移,但显著加剧了轮对横移运动,这不利于车辆高速运行,应及时避免。
4 结论
1)4 种不同类型轮径差都会对车轮磨耗产生影响,随着轮径差的不断增大,踏面磨耗显著加剧,车轮磨耗速率显著增大;
2) 轮径差不仅会改变车轮踏面的磨耗区域,也会改变滚动接触疲劳和应力的分布区域,其中等值反向轮径差使车轮踏面磨耗区域向两侧方向扩展,其余3种轮径差使车轮踏面的磨耗区域向轮径大的一侧方向移动。
3) 轮径差会导致车轮踏面出现偏磨现象,使轮径大的车轮以踏面磨耗为主,轮径小的车轮以轮缘磨耗为主。等值同向轮径差工况下的偏磨最为明显。
4) 轮径差会导致轮对发生偏移且显著增大轮对横移量,从而使滚动接触疲劳区域扩大,这不仅会降低车轮使用寿命,还将严重影响车辆高速运行安全,应及时监测并镟修。
