基于层次分析法的路线规划算法的建模与仿真
2021-06-24杨晓敏李梓涵
杨晓敏,李梓涵
(运城学院数学与信息技术学院,山西运城 044000)
随着经济和社会的发展,人们对休闲娱乐的要求越来越高,大型游乐场成为了人们休闲娱乐的一个重要场所。人们在大型游乐场游玩时经常会面临着一些选择:游玩时如何选择游玩顺序才能省时又尽兴?而对于游乐场来说,同样需要考虑如何才能使游客有好的游玩体验的同时获得更高的收益。
游乐场内部项目的游玩规则分为两种:需要预约的和随时可以游玩的,需要预约的为项目A1~A11,随时都可以游玩的项目为B1~B27。购买通票和购买门票的游客都可以游玩A系列项目和B系列项目。该游乐场售票采用现场售票和网上售票两种,网上的票价以所规定票价的9 折出售,现场售票在每天的早上8:00开始。游客8:30开始入场,9:00整各个项目开始开放。下午结束的时间分为两种,冬季作息时间,室外游乐场项目17:30 结束,室内游乐场19:00 结束;夏季作息时间,室外游乐场19:00 结束,室内游乐场20:00结束。
针对某个大型游乐场的部分运营数据,预测未来游客的数量。某游客计划在2019 年8 月5 日到该游乐场购买通票游玩,通过对历史数据进行建模,找到最优的游玩顺序。
1 问题分析
项目游玩人数预测问题,需要根据历史数据来预测未来的数据据,首先分析了各个项目游玩人数和当天游客人数的关系,得出基于线性回归的预测模型[1-4],参考排队论[5-8],计算了8 月5 日的每个项目的排队人数和排队时间。通过对当天人数的预测,进一步进行游玩路线的规划。针对需要解决的问题,建立游乐场游客预测及路线规划模型结构示意图如图1。
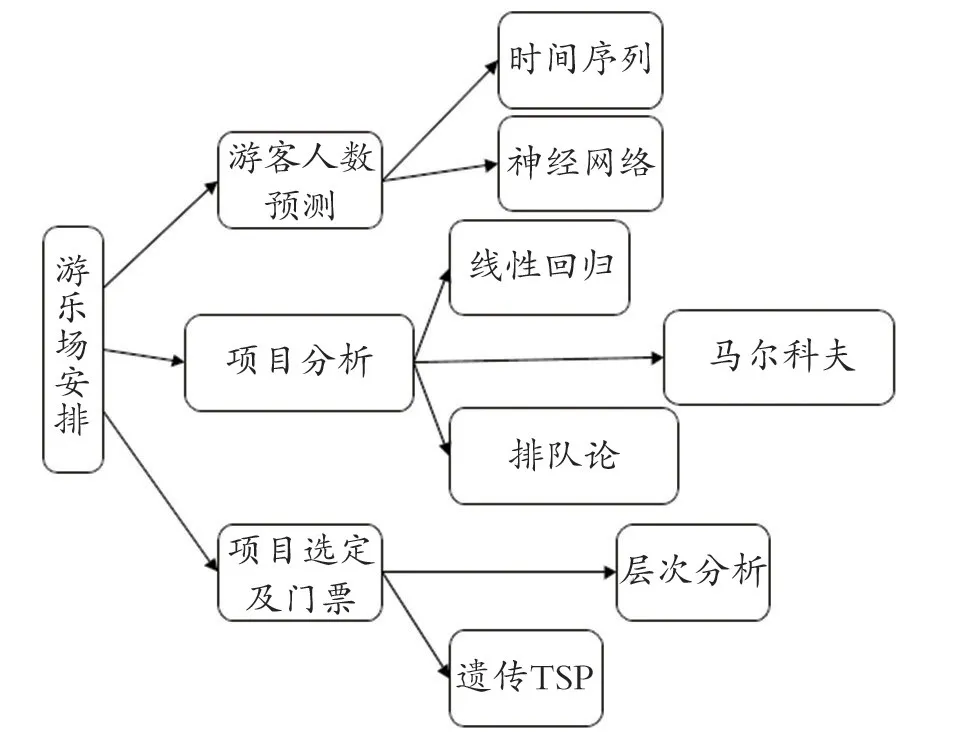
图1 游乐场游客预测及路线规划模型结构图
首先进行数据的预处理,主要是对数据进行了数据的质量分析、缺失值和异常值的删除;分析了各个项目游玩人数和当天游客人数的关系,得出基于线性回归的预测模型,参考排队论,计算了8 月5 日的每个项目的评价排队人数和排队时间;最后将游玩顺序问题分为三个部分,分别为项目评价、项目选择、游玩顺序确定。首先根据项目的特征如人数、收费、等待时间等建立了基于层次分析法[9-10]的项目顾客满意度评价模型;进一步地根据上述提供的满意度最大化作为优化目标,游玩时间作为限制条件建立了基于多元线性规划的项目选择模型,得出最大满意度的项目选择;最后定义了项目游玩的平衡指标,将上述项目选择结果建立相关的图论模型通过遗传算法得出类旅行商的具体游玩顺序,由此确定了游客路线规划模型并得到其价格的评估模型。
2 游乐场游客预测及路线规划模型的建立与求解
2.1 数据预处理
因为数据存在着许多脏数据,缺省数值。使用这些未经处理过的数据在一定程度上会对模型的建立过程中带来很多不必要的麻烦,对模型的输出也会造成极大的干扰作用,甚至还会得到错误得结果。所以,应在模型建立之前对数据进行合理,适当的预处理。主要针对其缺失值进行去除处理,然后在针对其不在其正常范围区间的值进行去除,并对异常数据进行了处理。
2.2 基于多无线性回归的项目游玩人数预测模型
项目游玩人数预测问题,分析了各个项目游玩人数和当天游客人数的关系,得出基于线性回归的预测模型。具体过程如下,通过已有的数据,建立多元线性回归的预测模型。首先在数学关系先假设存在的线性关系:

根据线性回归方法,编程预测出在2019 年8 月5日A4,B5,B12,B25 四个项目当天的游玩人数分别是9 746,9 302,354,8 922。
2.3 参考排队论理论
可以得到平均排队队伍长度为:

由此可以得到其各个项目的排队队伍长和排队时长见表1。
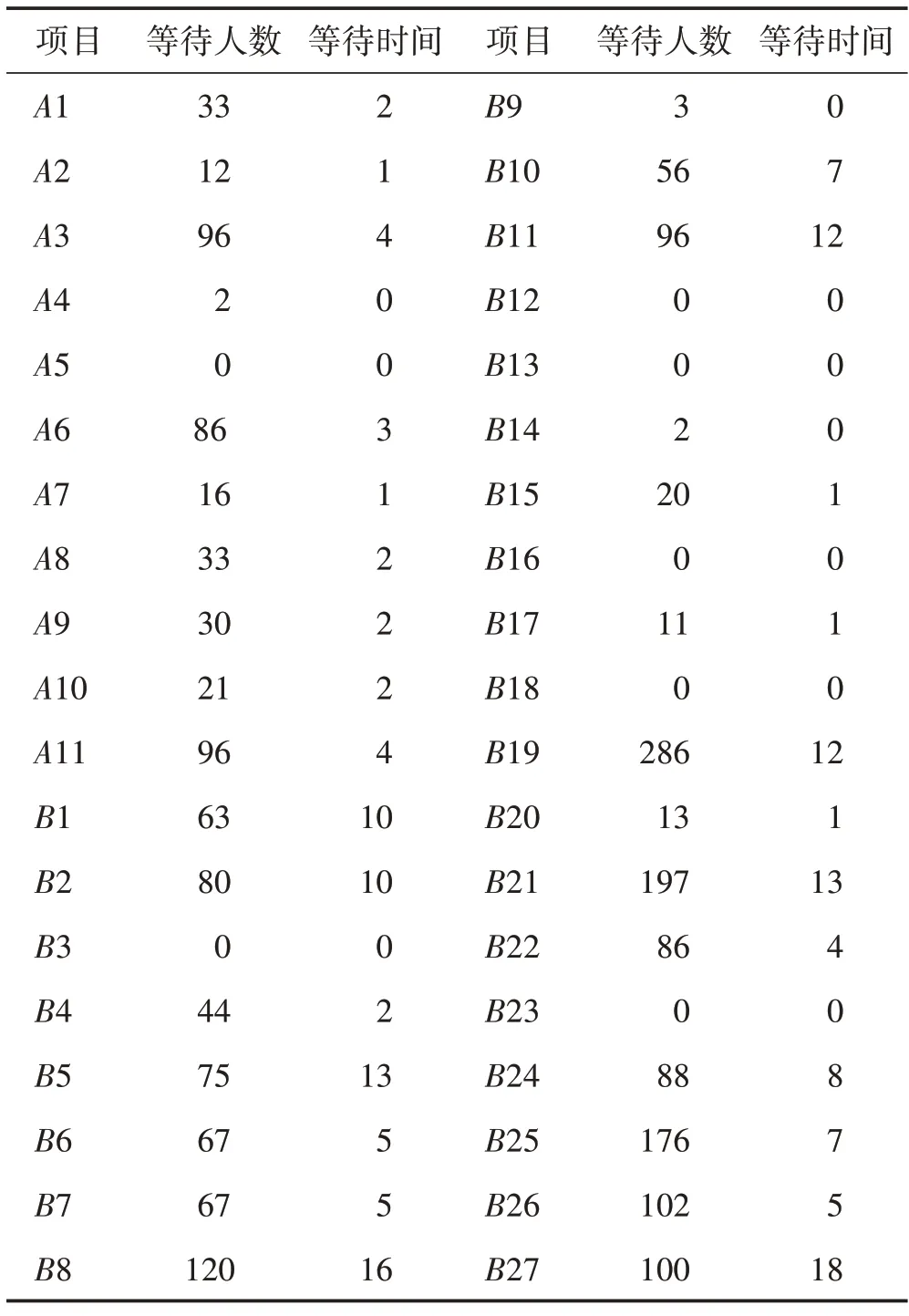
表1 各个项目的排队人数和时长结果
3 基于层次分析法的项目顾客满意度评价模型
层次分析法是一种定性与定量相结合的系统分析法,根据问题的总目标,以系统化的观点,把问题分解成若干因素,并按其支配关系构成的递阶层次结构模型,然后运用两两比较的方法确定决策方案的重要性,从而获得满意的决策。
3.1 构造层次结构图
人们选择游玩项目时主要考虑项目的时间效率、项目吸引力、项目的可玩性等三方面的性能,将决策的目标、考虑的因素(决策准则)和决策对象按它们之间的相互关系分为最高层、中间层和最低层,绘出层次结构如图2。
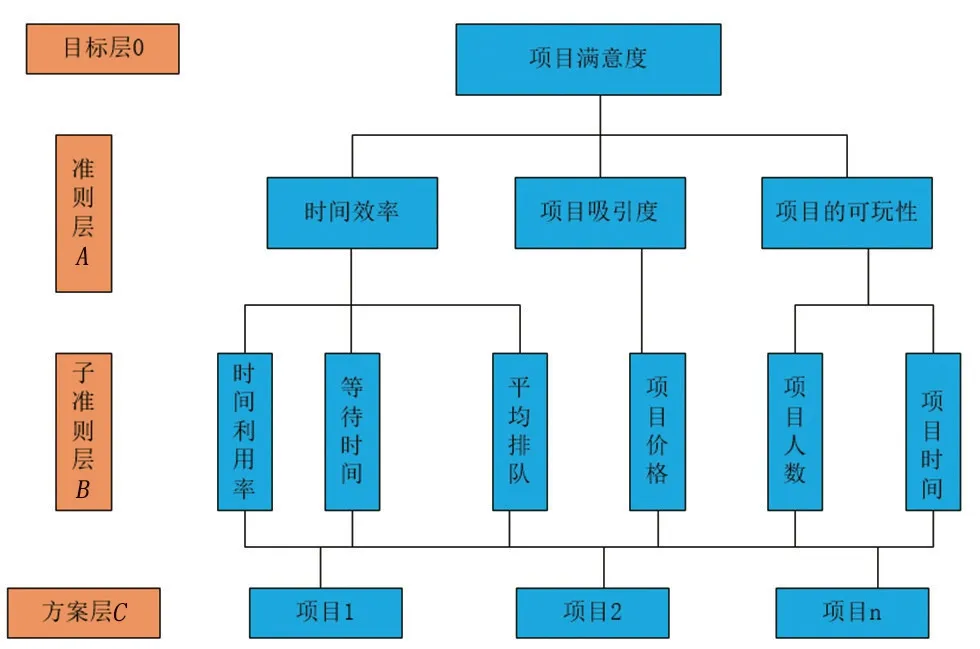
图2 层次分析结构示意图
3.2 构造对比矩阵
在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不易被别人接受,因而采用了Santy 等人提出的一致矩阵法,即不把所有因素放在一起比较,而是两两相互比较,此时采用相对尺度,尽可能减少性质不同的诸因素相互比较的困难,以提高准确度。
判断矩阵是表示本层所有因素针对上一层某一个因素的相对重要性的比较。判断矩阵的元素用Santy 的1~9 标度方法给出。通常用1~9 及其倒数作为程度比较标准,即九级标度法见表2。

表2 九级标度法含义表
根据上述程度比较表格,得到各个层次的对比矩阵。
A层对目标层的对比矩阵:

B层对A层的对比矩阵:
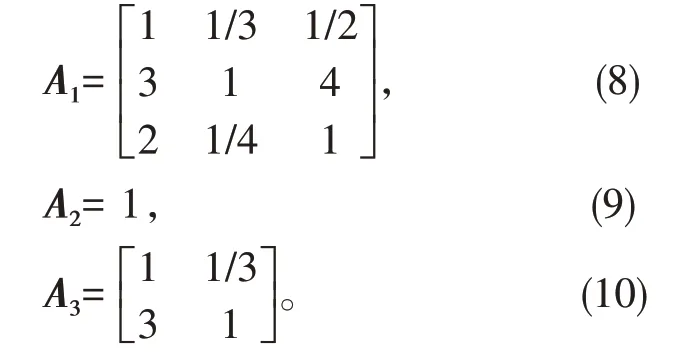
C层对B层的对比矩阵:

3.3 进行一致性检验并计算权向量
在得到相关对比矩阵之后,需要确保其中各个赋值整体的一致性,所以进行了一致性检验,其中一致性指标其具体:

一致性检验需要满足:
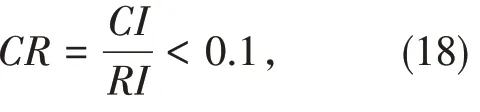
其中随机一致性指标RI与n有关,具体数值见表3。
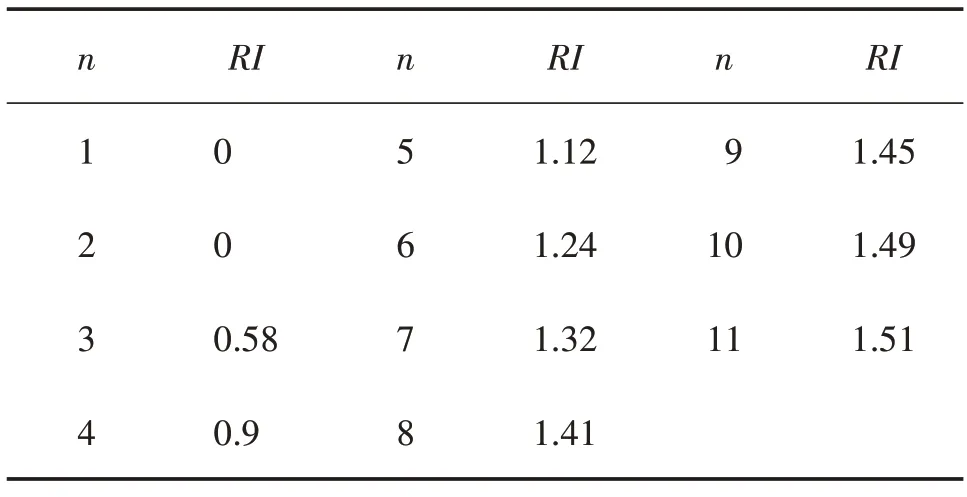
表3 RI数值参考表格
根据上述计算公式,得到各个对比矩阵一致性检验结果见表4。

表4 一致性检验结果
从上表中可以看到各个对比矩阵一致性检验均满足要求,根据上述模型最后得到的游客对各个项目的的喜爱程度见表5。

表5 各个项目的满意度表
4 基于多元线性规划的项目选择模型
在前面的基础上建立了相关多元线性规划模型,其主要是以各个项目的满意度为基础,以时间为约束条件,以最大化满意度为目标建立多元线性规划模型,其中对是否选择项目使用0-1 变量进行表达,为了方便使用matlab求解函数进行求解本文把优化目标加一个负号变成最小化的优化模型,得出其优化目标为:

采用单纯形法进行求解。其具体求解步骤如图3。

图3 单纯形法算法流程图
先确定一个初始可行解,然后检查基本解是不是最优的,如果最优则停止迭代,已找到最优值,如果不是进行下一步,移至目标函数值有所改善的另外一个基本可行解,重复之前步骤。
在确定了相关的项目内容后,具体确定其项目的顺序,参考关联度系数的计算方式来定义项目之间的二维距离关系然后构建遗传算法求解类TSP 模型,其具体距离定义关系式:
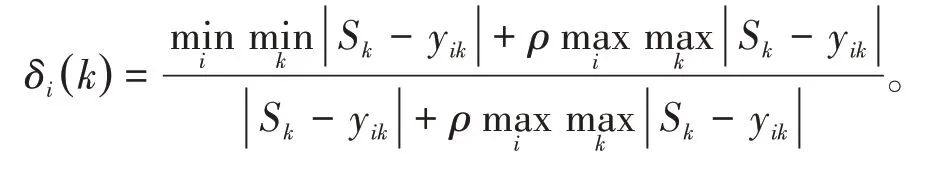
最后用计算机编程获得最后的结果,游玩顺序如图4。
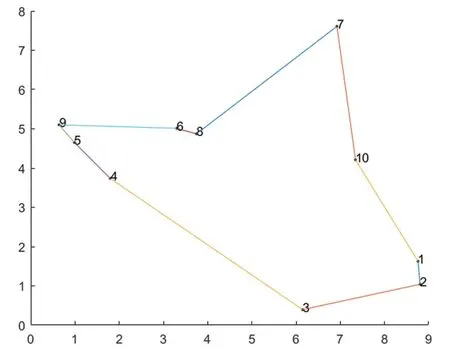
图4 项目游玩顺序
通过遗传算法进行优化求解,算法迭代很快,适应度曲线变化示意如图5。
图5 适应度曲线变化示意图
5 结论
首先根据历史数据,建立线性回归模型,预测计算了2019 年8 月5 日A4,B5,B12,B25 四个项目当天的游玩人数,并通过排队论,计算了每一个项目的平均排队人数和平均等待时间。用层次分析法,构造了对比矩阵,得到了各个项目的满意度表,最后用遗传优化的类TSP方法得到了最佳游玩顺序。
