对变燃速发射药密闭爆发器实验曲线的模拟计算*

张丽华， 代淑兰

(1. 中北大学 化学工程与技术学院， 山西 太原 030051； 2. 中北大学 环境与安全工程学院， 山西 太原 030051)

0 引 言

双层管状变燃速发射药的外层药燃速低于内层药燃速， 使发射药呈现出燃烧渐增性[1，2]. 之前对这种变燃速发射药的燃气生成规律进行理论公式推导和计算时， 是在假设发射药燃烧服从几何燃烧定律的条件下推导得到的理论公式[3]， 并且依据变燃速发射药燃烧时的燃去质量分数ψ与气体生成猛度Γ理论公式， 讨论各参量改变时Γ-ψ理论计算曲线所呈现的变化规律状况， 也是在假设所有发射药的药粒尺寸完全一致、 所有药粒同时被点燃的前提下才能出现的理想状况.显然， 这种假设条件与实际发射药的实验测试条件有着较大差别， 使得这种理论计算曲线与实际发射药的密闭爆发器实验曲线差异较大[4-9].由于在进行实验测试时， 处于密闭爆发器内的发射药各部分药粒被点燃的先后次序应该是有差别的， 尽管各部分药粒被点燃的先后时间差可能并不大， 但考虑到从点火药点火开始到所有药粒燃完的整个时间过程也很短， 因而各部分药粒被点燃的先后差别对发射药所表现出的整体燃烧性能是有影响的.因此， 本文针对各部分药粒被点燃先后的差别对变燃速发射药的Γ-ψ理论曲线所带来的影响进行了理论研究， 提出了一种模拟计算方法.

1 双层管状变燃速发射药燃气释放规律的理论计算公式

对于如何把变燃速发射药各部分药粒在密闭爆发器中被点燃的先后差别对其实验曲线的影响在理论计算中展现出来的问题， 一种解决思路是把所有药粒按照质量划分为若干个具有不同质量分数的部分， 所有部分的质量分数之和应等于1. 假设所有的药粒具有相同的药型尺寸和内外层药燃速比， 只是所划分的各个部分是渐次被点燃的， 而同一部分中的药粒假设在相应的时刻被同时点燃. 如此仍然可以采用以前推导的理论计算公式来计算每一部分药粒所贡献的燃去质量分数和气体生成猛度， 然后将各部分药粒燃烧对总的燃烧性能的贡献值进行加和， 便可得到所有药粒燃烧所产生的整个燃烧过程的Γ-ψ理论曲线.

在本文进行的变燃速发射药各部分渐次被点燃的模拟计算中， 仍然假设发射药燃烧服从几何燃烧定律， 而且长径比足够大(即可以忽略药粒端面燃烧造成的影响， 以突出双层变燃速发射药因内外层燃速差和药层厚度不同所造成的燃烧渐增性变化)[4]， 外层药与内层药的燃速比为k， 并且k<1； 发射药的燃速与压力呈正比关系， 内层药的燃速系数为u1.计算中采用的双层管状变燃速发射药的初始几何尺寸符号如图1 所示.当外层药燃完时刻， 药粒的外径D=Dh， 孔径d=dh.

图1 双层管状变燃速发射药试样的初始几何尺寸示意图

令ψ0、Γ0分别表示按照以前推导的理论公式计算的变燃速发射药燃去质量分数和气体生成猛度， 它们是对应于所有药粒同时被点燃时的理论计算值[3].假设把所有药粒划分为N个渐次被点燃的燃烧部分， 其中第i个部分的质量分数为wi， 该部分发射药所贡献的燃去质量分数和气体生成猛度分别为ψi、Γi， 则在理论计算中采用了下列公式：

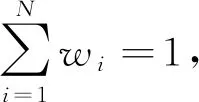
(1)

式中：N为将所有药粒划分的燃烧部分数目；wi为第i个燃烧部分在所有药粒中所占的质量分数.

ψi=wi·ψ0,

(2)

Γi=wi·Γ0,

(3)

(4)

(5)

式中：ψi、Γi分别为第i个燃烧部分所贡献的燃去质量分数和气体生成猛度数值；ψ0、Γ0分别为采用后面式(6)～式(9)计算得到的燃去质量分数和气体生成猛度数值.

(6)

(7)

(8)

(9)

(10)

式中：D0、d0、L分别为管状变燃速发射药初始的外径、 孔径、 长度；d为发射药燃烧过程中某时刻的孔径；Dh、dh分别为变燃速发射药的外层药刚燃完时刻对应的外径、 孔径；k为变燃速发射药的外层药与内层药的燃速比；y为内层药与外层药的密度比；u1为内层药的燃速系数；x=d-d0,x1=d-dh,L1=L-(dh-d0).

2 双层管状变燃速发射药渐次点燃的Γ-ψ理论计算曲线

在等分划分各燃烧部分的条件下， 计算得到N分别取不同值时的Γ-ψ理论计算曲线(如图2 所示).由图2 可见， 将变燃速发射药划分为若干部分渐次被点燃的理论计算曲线明显比假设全部药粒同时被点燃时的理论计算曲线(N=1时)要更为接近密爆实验曲线的情况； 在所划分的各燃烧部分所占质量分数相等的条件下，N值较大时，Γ的最大值相对较小， 并且在其他参数相同的条件下，Γ最大值所对应的ψ值随着N值增大呈现出先增大而后又减小的变化趋势.

图2 将变燃速发射药划分为不同数目的燃烧部分渐次

双层管状变燃速发射药在密闭爆发器中渐次被点燃的各部分所占质量分数发生变化时如何影响Γ-ψ理论曲线？本文中对此进行了模拟计算， 将全部药粒划分为9个燃烧质量部分， 对应于表1 中列出的5种各燃烧部分质量分数取值条件下的理论计算曲线如图3 所示.

表1 用于理论计算的各燃烧部分所占质量分数的取值

从图3 的计算结果可见， 在其他参数取值相同的前提下， 相比于各部分所占质量分数较为均分(取值1)的情况， 当被点燃部分所占质量分数较大者较为靠前时(即占比较多的药粒在较早时刻被点燃)， 变燃速发射药燃烧所呈现的Γ最大值相应会有所增大(如取值2和取值3的曲线)， 并且Γ最大值所对应的ψ值有移向较大值处的趋势； 而当被点燃部分所占质量分数较大者较为靠后时(即占比较多的药粒在较晚时刻被点燃)， 变燃速发射药燃烧所呈现的Γ最大值相应会有所降低(如取值4和取值5的曲线)， 并且Γ最大值所对应的ψ值有移向较小值处的趋势.图3 还显示出， 如果较多数量的药粒比较滞后被点燃， 则其燃烧所呈现的Γ-ψ曲线将会在较宽的ψ值变化范围内具有相对稳定的Γ值.

图3 各燃烧部分所占质量分数不同时的Γ-ψ理论计算曲线

为了考察双层管状变燃速发射药的外层药与内层药燃速比k对其理论Γ-ψ曲线状况的影响， 在将药粒划分为9个燃烧部分的质量分数取值采用表1中取值1的条件下， 模拟计算了不同k值条件下所呈现的Γ-ψ曲线， 所得果如图4 所示.

图4 显示出， 在各燃烧部分所占质量分数基本相等(即药粒较为匀速地渐次被点燃)的条件下，k值较小(即内、 外层药的燃速差别较大)时，Γ的最大值较小， 并且Γ最大值所对应的ψ值相对较大. 这意味着在相同的药型尺寸条件下， 变燃速发射药的内、 外层药的燃速差别较大时， 其燃烧渐增性会表现得较强， 这也符合一般变燃速发射药的基本原理[10].

图4 不同燃速比k取值条件下的Γ-ψ理论计算曲线

在将药粒划分为9个部分的质量分数取值采用表1中取值1的条件下， 模拟计算了内层药的燃速系数u1取值不同时变燃速发射药所呈现的Γ-ψ理论曲线， 得到的结果如图5 所示.

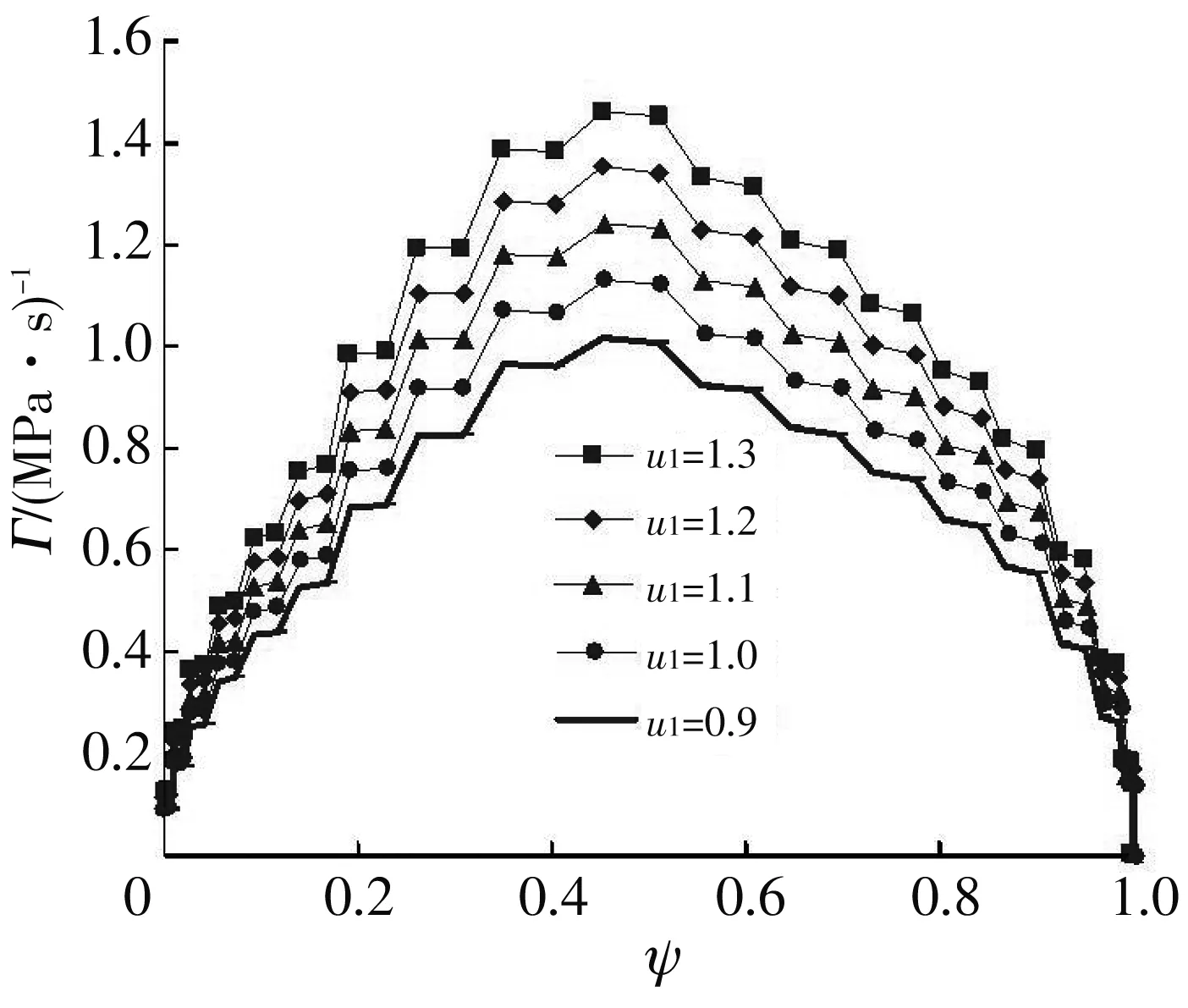
图5 不同内层药燃速系数取值条件下的Γ-ψ理论计算曲线

由图5 中的理论计算曲线可见， 在各燃烧部分所占质量分数基本相等的条件下， 内层药的燃速系数u1取值较小时，Γ的最大值较小， 但Γ最大值所对应的ψ值基本不变.这意味着在相同的药型尺寸和内外层药燃速比的条件下， 变燃速发射药的内层药燃速较低时， 其燃烧所呈现的Γ值也较小.

3 用渐次点燃的Γ-ψ理论曲线模拟变燃速发射药的密爆实验曲线

依据双层管状变燃速发射药试样的实际药型尺寸和实测的内外层药燃速参数值， 对两个变燃速发射药试样的密闭爆发器实验曲线按照各部分药粒渐次被点燃的方法进行了Γ-ψ理论曲线的模拟计算.

由上述理论计算曲线可以得知， 针对密闭爆发器实验所得到的Γ-ψ曲线情况， 可以通过改变所划分各燃烧部分的质量分数取值来使计算曲线更为接近实验曲线， 从而可以估计出对应这种发射药的密闭爆发器实验曲线， 发射药渐次被点燃的情况. 图6 中所示的是对应某一变燃速发射药试样的密闭爆发器实验得到的Γ-ψ曲线， 以该发射药的药型尺寸为计算基础， 通过考察所划分的各部分质量分数取值不同时的理论曲线状态， 得到了比较接近该实验曲线的理论计算曲线. 图6 中的理论计算曲线所采用的各部分质量分数取值是对应表1中取值1的情况， 由此可以得知该变燃速发射药试样在密闭爆发器实验中渐次被点燃的情况是一种较为匀速的逐步被点燃的情况.

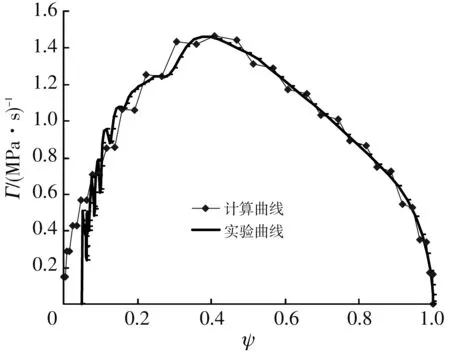
图6 第一种双层管状变燃速发射药试样的密爆实验曲线和渐次点燃的Γ-ψ理论计算曲线

通过对另一个变燃速发射药试样的密闭爆发器实验数据的处理可以得到其相应的燃速系数值， 以该变燃速发射药试样的药型尺寸和燃速系数为计算基础， 采用将药粒划分为9个质量部分渐次被点燃的理论计算方法， 也得到了比较接近该试样密爆实验曲线的Γ-ψ理论模拟计算曲线， 如图7 所示.从图7(b) 中所展示的获得较为接近该试样密爆实验曲线的Γ-ψ理论计算曲线所采用的各燃烧部分的质量分数取值可见， 与图6中的模拟计算曲线所采用的各燃烧部分的质量分数取值条件相比， 对应图7 中这种燃烧渐增性明显较强的变燃速发射药情况， 模拟计算中需要采用各燃烧部分中质量分数较大者处于较为滞后被点燃的取值， 才能获得与实验曲线较为接近的理论计算曲线， 也说明了有较多的药粒部分较迟被点燃时， 可使得发射药的燃气压力增速最大值出现得较晚， 表现出较好的燃烧渐增性.

(a) 密爆实验曲线及理论计算曲线

4 结 论

采用将变燃速发射药划分为若干质量分数不同的燃烧部分被渐次点燃的理论计算方法， 可以得到与变燃速发射药密闭爆发器实验曲线较为相近的Γ-ψ理论模拟计算曲线. 本文中所讨论的理论计算时划分各燃烧部分质量分数取值情况以及各参量变化对Γ-ψ理论计算曲线的影响规律， 可以为设计燃烧渐增性更为合理的变燃速发射药提供有价值的理论参考依据.