奥氏体不锈钢深冷容器疲劳设计曲线探讨
2021-06-24郑津洋王振宇陆群杰刘宝庆李克明吴英哲
郑津洋,王振宇,陆群杰 ,刘宝庆,李克明,吴英哲,徐 平
(1.浙江大学 化工机械研究所,杭州 310027;2.浙江大学 应用力学研究所,杭州 310027)
0 引言
近年来,高速增长的天然气、氢气等能源气体和氧、氮、氩气等工业气体需求,推动了深冷容器市场的迅速发展[1-4]。奥氏体不锈钢因具有良好的低温力学性能、耐腐蚀性能、焊接性能、成形性能,且无韧脆转变温度,成为深冷容器(尤其是内容器)的主要应用材料[5-7]。深冷容器在使用中常承受频繁加卸载、振动等因素引起的交变载荷,导致容器疲劳损伤甚至失效。随着深冷容器使用量增加,因疲劳断裂导致失效的案例(如液氧储罐[8]等)越来越得到关注,深冷疲劳性能越来越受到重视。
奥氏体不锈钢的低温疲劳特性是评价深冷容器全寿命周期安全性的重要依据。目前,国内外已对奥氏体不锈钢的深冷疲劳性能作了较多研究。NACHTIGALL[9]对10种低温常用金属材料(包括奥氏体不锈钢AISI304和AISI310)在室温(约300 K)、液氮温度(77 K)和液氦温度(4 K)下进行了疲劳试验,发现奥氏体不锈钢的低周疲劳寿命随温度降低而降低,而高周疲劳寿命随温度降低而升高。此外,WU等[10-13]对S30408深冷(77 K)低周疲劳性能进行了大量试验研究,发现在小应变幅(小于0.75%)时,得益于材料低温下的强度增加,S30408低周疲劳寿命较室温下显著提高;但随应变幅增至0.75%以上,疲劳性能更多地由塑性决定时,其深冷疲劳寿命则比室温短。可见,奥氏体不锈钢深冷S30408疲劳特性与常温相比存在较大差异,同时,由于该材料在低温、应变幅等影响下易发生组织转变,使得其深冷疲劳性能表现更为复杂。
然而,现行国内外压力容器标准,如JB/T 4732—1995(2005年确认)[14]、ASME BPVC Ⅷ-2—2019[15]、EN 13445-3:2014[16]等提供的疲劳设计曲线均针对常温或高温工况(如表1所示),并未考虑深冷对材料强度和疲劳性能的影响,不利于充分利用材料性能。因此,为节约材料、降低成本,在安全前提下实现轻量化设计制造,针对奥氏体不锈钢的疲劳问题,提出适用于深冷工况的深冷疲劳曲线及其获取方法具有实际意义。

表1 现行压力容器标准中疲劳设计曲线温度适用范围
受限于低温疲劳试验条件,在任意深冷温度下进行大量疲劳试验数据来获取疲劳寿命曲线的成本和难度较高。因此,基于现有常温疲劳曲线进行修正,并选取少量温度点进行验证是建立疲劳曲线一种经济可行的方法。弹性模量修正是常用方法之一,现有高温疲劳设计就是通过引入不同温度下弹性模量修正系数实现的[15]。然而低温下,NYILAS等[17]测得316LN在77,4 K温度下弹性模量分别为204,206 GPa;BOTSHEKAN等[18]测得316LN 在300,77K温度下弹性模量分别为193,205 GPa;另外,NACHTIGALL[9]测得304L在300,78,4 K温度下弹性模量分别为190.2,205.1,201.3 GPa。可见,温度从300 K降低至4 K,奥氏体不锈钢材料弹性模量未出现明显变化(小于8%),其改变远不如疲劳寿命显著。因此,通过弹性模量修正方法难以准确表征深冷疲劳曲线。
本文提出一种基于现有常温疲劳设计曲线和深冷力学性能,获取奥氏体不锈钢深冷疲劳设计曲线的方法。首先,基于文献中77 K和4 K温度下奥氏体不锈钢疲劳数据,采用Langer模型描述得到77 K和4 K温度下奥氏体不锈钢疲劳试验曲线;其次,通过建立Langer模型中疲劳极限以及塑性应变项系数与温度的关联关系,在上述温度77 K和4 K奥氏体不锈钢疲劳试验曲线基础上,对现有常温疲劳曲线进行修正,以获得不同温度下的深冷疲劳设计曲线;最后,对根据本文方法得到的110 K温度下奥氏体不锈钢疲劳设计曲线与文献中相关试验数据以及ASME BPVC Ⅷ-2疲劳设计曲线进行对比分析,验证本文方法的有效性,以期为深冷压力容器疲劳设计提供思路。
1 深冷疲劳试验曲线
1.1 疲劳寿命模型
Langer模型是美国工程师LANGER[19]基于Manson-Coffin公式[20-21]提出的一种疲劳试验曲线拟合模型,并考虑了塑性应变幅和弹性应变幅的影响,见下式:
(1)
式中,S为虚拟应力幅值,MPa;Nf为疲劳寿命;σ-1为弹性应变幅即疲劳极限,MPa;C为塑性应变项系数,与断面收缩率、断后伸长率等塑性参数有关,在应力水平较低时占主导地位,其值可取C=(E/4)ln[100/(100-RA)]来估算(其中RA为材料的断面收缩率(%);E为弹性模量,MPa)。
Langer模型由于形式较为简单,引入参数较少,适用于多种相近材料共同拟合,在疲劳试验中广泛使用。此外,由于Langer模型反映了疲劳极限的存在,与压力容器用钢的实际情况相符[22],因而现行ASME BPVC Ⅷ-2疲劳试验曲线也基于Langer模型来建立[23]。
因此,本文采用Langer模型,对低温下300系列奥氏体不锈钢的疲劳曲线计算方法进行探讨。
1.2 基于Langer模型的疲劳试验曲线
在现有奥氏体不锈钢深冷疲劳特性研究中,轴向等幅拉压疲劳(应变比R=-1)数据较为常见,ASME BPVC Ⅷ-2中的疲劳设计曲线即采用了轴向等幅拉压疲劳试验结果[23]。因此,本文主要基于文献中轴向等幅拉压疲劳试验数据进行分析。
1.2.1 常温
常温下,ASME BPVC Ⅷ-2标准释义ASME PTB-1—2014[23]中给出了300系列奥氏体不锈钢原始试验数据,以及采用Langer模型描述疲劳试验曲线的最佳拟合参数,如图1[23]所示。

图1 ASME PTB-1—2014中常温下奥氏体不锈钢疲劳试验曲线Fig.1 The fatigue test curve for austenitic stainless steels at ambient temperature from ASME PTB-1—2014
随后,根据ASME BPVCⅡA—2019[24]材料标准取弹性模量E=195 GPa,得到常温下疲劳试验曲线拟合公式,如式(2)所示。
(2)
1.2.2 温度77 K
在郑津洋团队[10]试验获得的国产S30408深冷疲劳数据基础上,进一步收集文献[9,18,25-30]中奥氏体不锈钢在77 K温度下的疲劳寿命数据,并采用Langer模型进行拟合(如图2所示),得到77 K温度下奥氏体不锈钢疲劳试验曲线拟合式,如式(3)所示。
(3)

图2 奥氏体不锈钢疲劳试验曲线(温度77 K) Fig.2 The fatigue test curve for austenitic stainless steels at 77 K
1.2.3 温度4 K
类似地,收集文献[9,26,28]中4 K温度下奥氏体不锈钢的疲劳试验数据,并用Langer模型进行拟合,如图3所示。得到采用Langer模型描述的4 K温度下奥氏体不锈钢S-N曲线拟合式,如式(4)所示。
(4)
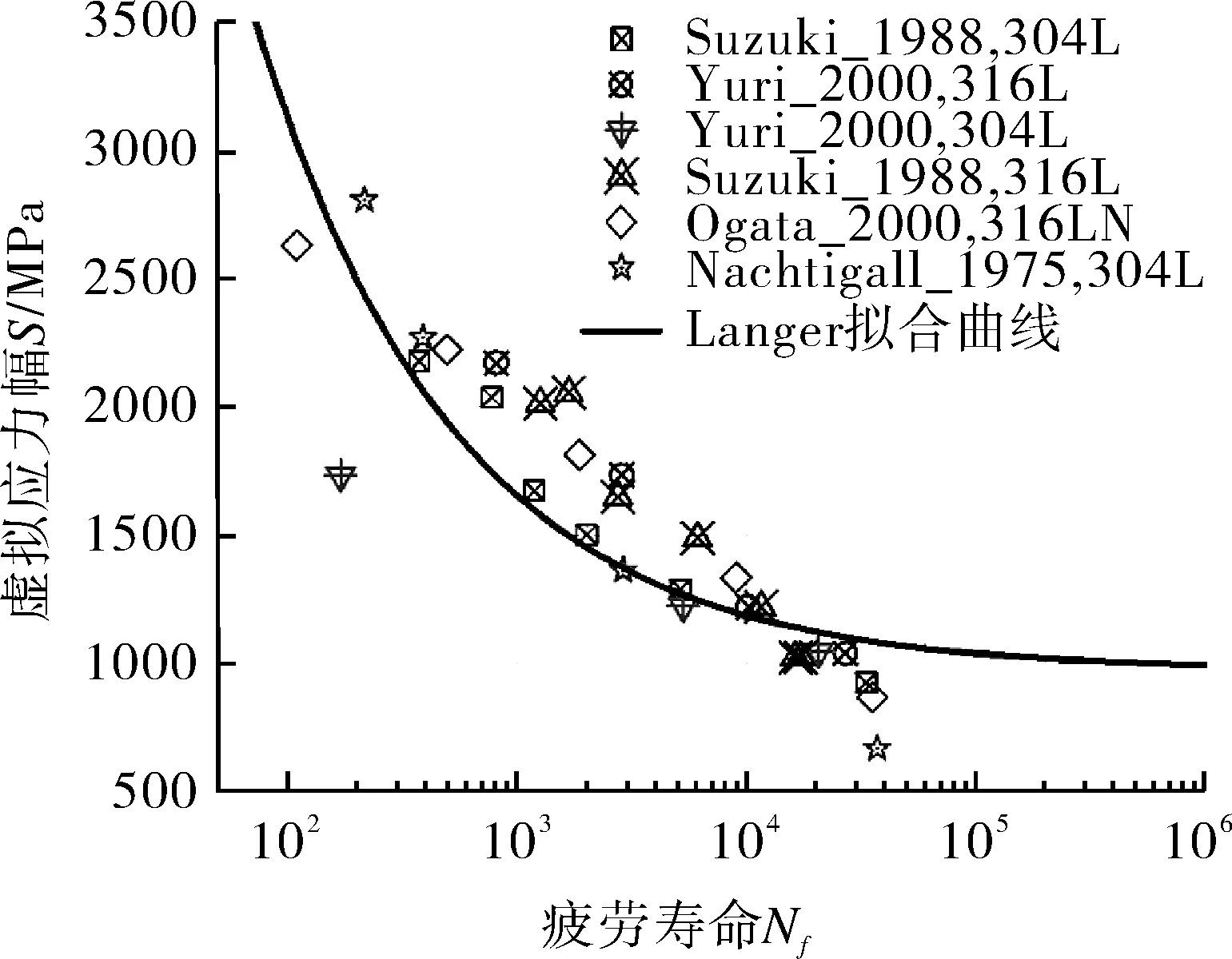
图3 奥氏体不锈钢疲劳试验曲线(温度4 K) Fig.3 The fatigue test curve for austenitic stainless steels at 4 K
1.3 对比分析
将上述常温、77 K和4 K温度下通过Langer模型拟合的奥氏体不锈钢疲劳试验曲线进行对比,如图4所示。

图4 不同温度下奥氏体不锈钢疲劳试验曲线对比 Fig.4 Comparison of fatigue test curves for austenitic stainless steels under different temperatures
由图4可以看出,深冷奥氏体不锈钢疲劳试验曲线较常温有明显差异。随着温度降低,奥氏体不锈钢疲劳极限提高,温度77,4 K疲劳试验曲线与常温曲线的交点逐渐上移。可见,若在压力容器常见疲劳寿命区间(103~106次)采用深冷疲劳曲线,与现行常温疲劳曲线相比,将有利于提高使用寿命。因此,提出深冷疲劳设计曲线计算方法十分必要。
2 深冷疲劳设计曲线获取方法
2.1 方法依据
WU等[10]对77 K温度下奥氏体不锈钢的疲劳性能进行了系统研究,指出深冷对S30408材料疲劳寿命的影响在高应变幅区和低应变幅区有所区别,并分别将其归因于深冷对材料弹性和塑性的影响。YURI等[26]对比了SUS304L,SUS316L在4,77,293 K三个温度下的疲劳寿命曲线,发现这两种材料疲劳强度与屈服强度之比不随温度变化而变化。JEONG等[31]对304L等奥氏体不锈钢进行了应变控制的疲劳试验,其将温度对疲劳寿命的影响与宏观力学性能(包括屈服强度及抗拉强度)相关联,证明了用宏观力学性能参数预测疲劳寿命的可行性。
因此,基于常温疲劳曲线,可以通过考虑低温对材料塑性及材料强度的影响,建立Langer模型中疲劳极限(与强度有关)和塑性应变项(与断后伸长率有关)系数与温度的关联关系,来预测奥氏体不锈钢的深冷疲劳曲线。
2.2 深冷疲劳极限
对文献[9-10,18,23,26,28]中低温疲劳性能数据用Langer模型进行拟合,得到每组材料的疲劳极限(σ-1),如表2所示。进一步分析上述材料低温下的疲劳极限与材料屈服强度(Rp0.2)的关系,如图5所示。

表2 奥氏体不锈钢低温疲劳极限计算结果

图5 奥氏体不锈钢低温下疲劳极限与屈服强度关系
由图5可以看出,疲劳极限和屈服强度在不同温度下表现出相似的发展趋势,且疲劳极限与屈服强度间存在较强的相关性。因此,采用线性拟合描述低温下疲劳极限随屈服强度的变化趋势,如式(5)所示,其拟合决定系数为0.89。因此,可以通过低温对材料拉伸力学性能的影响来描述疲劳极限。式(5)的拟合数据(见表2)涵盖304,304L,316L,306LN等材料在77 K和4 K温度下的疲劳性能,因此该式适用于上述材料和温度范围。
σ-1=1.14Rp0.2+418.63
(5)
另外,日本原子能机构[32-33]给出了奥氏体不锈钢基于室温强度的低温强度预测公式,如式(6)所示。
(6)
式中,RT为温度T下的屈服强度,MPa;RTamb为室温屈服强度,MPa;T为温度,K;Tamb为室温,一般为293 K;B1,B2,B3为拟合参数。
由式(5),(6)可得,低温疲劳极限和温度的关系式如下:
式中,C1,C2为拟合参数,C1=σ-1,293K-418.63 MPa,C2=418.63 MPa。对于给定材料,其疲劳极限σ-1,293K值为常数,因此式(7)可进一步表示如下:
(8)
式中,D1,D2,D3为拟合参数。
随后,将上文中采用Langer模型拟合得到的293,77,4 K温度下疲劳试验曲线中的疲劳极限值代入式(8),即可确定式(8)中的拟合参数,并得到疲劳极限的计算公式如下:

+3.2798]
(9)
2.3 深冷塑性应变项系数
对于塑性应变项,其系数可以通过单轴拉伸(N=1/4)试验的断裂塑性来保守估算[20]。另外,由于断裂塑性和断后伸长率线性相关[34],为便于收集数据并简化表述,因此采用断后伸长率(A)来表征断裂塑性。通过低温拉伸试验并收集文献[26,28,35-40]中低温下奥氏体不锈钢断后伸长率数据,得到断后伸长率与温度关系,如图6所示。

图6 低温下奥氏体不锈钢断后伸长率A与温度T关系 Fig.6 The relation between temperature T and elongation at fracture A of austenitic stainless steels at low temperatures
由图6可以看出,低温下奥氏体不锈钢断后伸长率和温度呈线性相关,其线性拟合决定系数为0.91。因此,同样可以线性拟合塑性应变项系数和温度关系,得到低温下塑性应变项系数计算公式如下:
(10)
2.4 深冷疲劳曲线计算公式
综上,根据Langer模型可得奥氏体不锈钢基于常温疲劳性能的深冷疲劳试验曲线计算公式如下:
(11)
其中:
式中,rp,re分别为考虑低温影响的塑性应变项和疲劳极限的修正系数。
考虑到目前深冷疲劳数据较少的实际情况,本文研究主要基于304,304L,316,316L和316LN在77,4 K温度下的疲劳特性展开,提出的深冷疲劳曲线计算公式适用于上述材料,其他材料适用性尚待进一步研究。
根据目标温度,在式(11)基础上进一步按ASME BPVC Ⅷ-2中方法进行平均应力修正,并选安全系数(2/20)后取较小值后,即可获得深冷温区奥氏体不锈钢疲劳设计曲线。
3 验证与讨论
为验证上述深冷疲劳曲线计算方法的有效性,采用文献[41-43]中110 K温度下疲劳试验数据进行验证分析,并与计算结果(预测疲劳试验曲线)以及进一步选取安全系数(2/20)后获得的预测疲劳设计曲线和标准疲劳设计曲线进行对比分析。
将温度T=110 K代入式(11),得到110 K下的预测疲劳试验曲线拟合式,如式(12)所示。
(12)
将式(12)预测疲劳试验曲线与文献中110 K温度下疲劳试验数据及其直接拟合曲线一并作图,然后将预测疲劳试验曲线按ASME BPVC Ⅷ-2方法取应力安全系数2和寿命安全系数20得到的较小值作为该温度下的预测疲劳设计曲线,并将其与ASME BPVC Ⅷ-2中奥氏体不锈钢疲劳设计曲线进行对比,如图7所示。
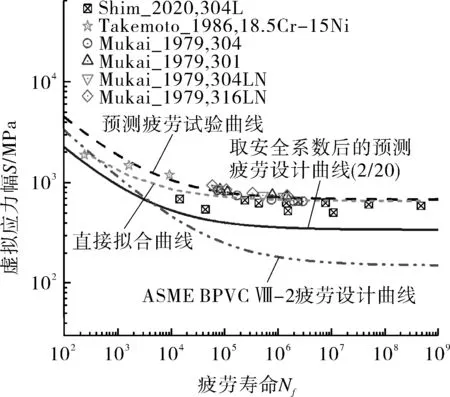
图7 奥氏体不锈钢深冷疲劳设计曲线与试验数据和 标准疲劳曲线对比 Fig.7 Comparison of cryogenic design fatigue curves of ASS with test data and standard fatigue curves
由图7可以看出,奥氏体不锈钢低温疲劳性能由于试样加工、尺寸、试验条件等误差,试验数据较为分散,分布在本文提出的预测疲劳试验曲线附近。与直接拟合曲线相比,在疲劳寿命低于105次范围内,直接拟合曲线略低于预测疲劳试验曲线;而当疲劳寿命高于105次时,直接拟合曲线与预测曲线则基本重合,可见本文方法具有较高的有效性。
至于在疲劳寿命小于105次时预测曲线略高于直接拟合曲线的原因,一方面在该范围内疲劳数据点较少,存在拟合误差;另一方面与进行塑性应变项系数低温修正时采用的线性关联存在偏差有关。在该范围内,疲劳试验应变幅较大,疲劳寿命更多由材料深冷塑性决定。本方法中塑性应变项系数低温修正时的关联关系基于低温拉伸性能的断后伸长率(A)建立,而采用A近似表征疲劳断裂塑性是存在偏差的。深冷温度下(如77 K),奥氏体不锈钢在大应变幅下的疲劳断口呈现一定的脆性断裂特征[12],而拉伸断口则仍呈明显剪切形貌特征[37]。由于采用断后伸长率表征疲劳断裂塑性未充分考虑该差异,从而使得预测曲线与直接拟合曲线存在一定偏差。
另外,相比考虑各种误差和数据分散性后得到的疲劳设计曲线,本文方法得到的疲劳设计曲线均位于试验数据下方,同时比ASME BPVC Ⅷ-2中的疲劳设计曲线更接近低温疲劳试验数据,尤其在高寿命区间。此外,预测疲劳设计曲线与ASME BPVC Ⅷ-2曲线在疲劳寿命103~104次之间相交,同时在低寿命(小于103次)时有数据点位于ASME BPVC Ⅷ-2曲线下方。可见,采用本文方法得到的预测疲劳设计曲线在低寿命区间更具安全性。
总之,通过试验数据初步验证,本文提出的深冷疲劳设计曲线计算方法是有效的。此外,本方法将有利于简化试验,节约试验时间和成本,具有实际意义。
4 结语
随着深冷容器疲劳性能研究的广泛开展和不断深入,奥氏体不锈钢低温下疲劳响应与常温下存在的明显差异越来越受到关注。然而,现行压力容器标准并未考虑低温对材料强度和疲劳的影响。随着深冷容器使用量增加,深冷疲劳失效越来越受到重视。因此,充分考虑低温对材料性能影响,对现有疲劳曲线进行修正,提出深冷疲劳设计曲线十分必要。本文基于ASME BPVC Ⅷ-2中常温疲劳曲线,分别考虑低温对Langer模型中疲劳极限项与塑性应变项的影响,建立了深冷疲劳试验曲线计算公式,并通过110 K温度下试验数据初步验证了本方法的有效性。因此,本文提出的深冷疲劳设计曲线,能够在保证安全的情况下充分考虑低温对材料疲劳寿命的影响,实现材料低温性能的充分利用,并为基于低温性能的深冷容器疲劳设计提供思路。
