空间绳网结构设计及优化方法
2021-06-24司骥跃庞兆君由锰冯广斌杜忠华
司骥跃,庞兆君,由锰,冯广斌,杜忠华
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.上海航天控制技术研究所,上海 200233)
0 引言
近20年,地球轨道飞行物数量从2000年的约11 000个激增到了2020年的近20 000个,在轨碰撞解体和爆炸解体事件时有发生,严重威胁着空间环境的安全[1-2]。为了应对空间碎片的威胁,人们提出了多种空间碎片清理方法[3-6],其中空间绳捕方法因其捕获距离远和抓捕容错率高等特点,在空间碎片清理方面具有良好的应用前景[7-8]。
欧洲航天局资助的“ROGER”项目对空间绳网系统的工作流程进行了详细规划[9]。Mao等将一个旋转绳网装置送入太空,并对空间环境下的绳网展开过程进行了初步研究[10]。同时,一些学者和机构开展了关于空间绳网展开及碰撞阶段的试验,包括零重力下的捕获试验和绳网下落试验等,验证了空间绳网方法的可行性[11-13]。英国萨里大学主导的“碎片清除”卫星于2018年4月初通过SpaceX的CRS-14号火箭发射到国际空间站,并在2018年9月19日首次在太空完成绳网抓捕测试[14]。
空间绳网系统的抓捕任务主要包含3个阶段:绳网展开阶段、接触碰撞阶段和网口可靠收紧阶段。其中碰撞、收口阶段主要关注绳网与目标接触后的状态,本文重点关注绳网与目标接触前的展开阶段。目前针对于展开阶段的研究主要集中在动力学建模、参数敏感性分析、高效展开方法3个方面。空间绳网的动力学建模方法主要有弹簧质点法[15-16]和绝对节点坐标法[17-18]。弹簧质点法在绳网展开阶段能够较好地模拟绳网的运动过程[18-19],且相比绝对节点坐标法具有更高的计算效率,现阶段研究多使用这种方法对绳网进行动力学建模。展开参数敏感性方面,主要的输入参数有发射速率、发射角度、牵引体质量占比和绳网材料参数等。考察的目标参数主要有绳网的展开时间、展开位移、最大展开率、有效展开位移等。现有的研究表明参数有发射速率、发射角度和牵引体质量占比这3项参数对绳网展开性能影响较大[20-23]。
现阶段绳网高效展开方法方面的研究并不多,高庆玉等[24]提出的“二级发射”模式使得绳网的最大展开面积以及飞行距离均优于传统的绳网发射模式。陈青全等[25]提出一种基于“定力撕裂带”的网型控制方法,通过在绳网边线安装定力撕裂带来抑制绳网的回弹现象。也有部分学者在研究过程中采用了不同构型的绳网,如平面绳网[26]、圆锥形绳网[27]、方锥形绳网[28]和半球形绳网[29]等。但是绳网构型的选择多是从功能性的角度考虑,如是否便于收纳和收口等。很少关注不同构型下展开性能的差异,且绳网网目均为规则多边形,并以四边形为主。
本文基于四边形平面绳网,在不改变绳网拓扑结构前提下通过优化网目结构,提升绳网的展开性能。通过引入矩阵表示绳网的拓扑结构及绳段长度,并使用弹簧质点法建立绳网动力学模型。提出通过控制绳网连接线落点实现网目结构优化的策略,进行数值仿真验证优化后的绳网相比未优化绳网的优势。
1 空间绳网结构及动力学模型
1.1 绳网结构
本文基于应用最广泛的四边形绳网开展研究,绳网4个网角依次连接有牵引体。将绳网的物理节点视为集中质量,物理节点之间的绳段视为弹簧和阻尼器并联的无质量单元,绳网的构型及离散方法如图1所示。
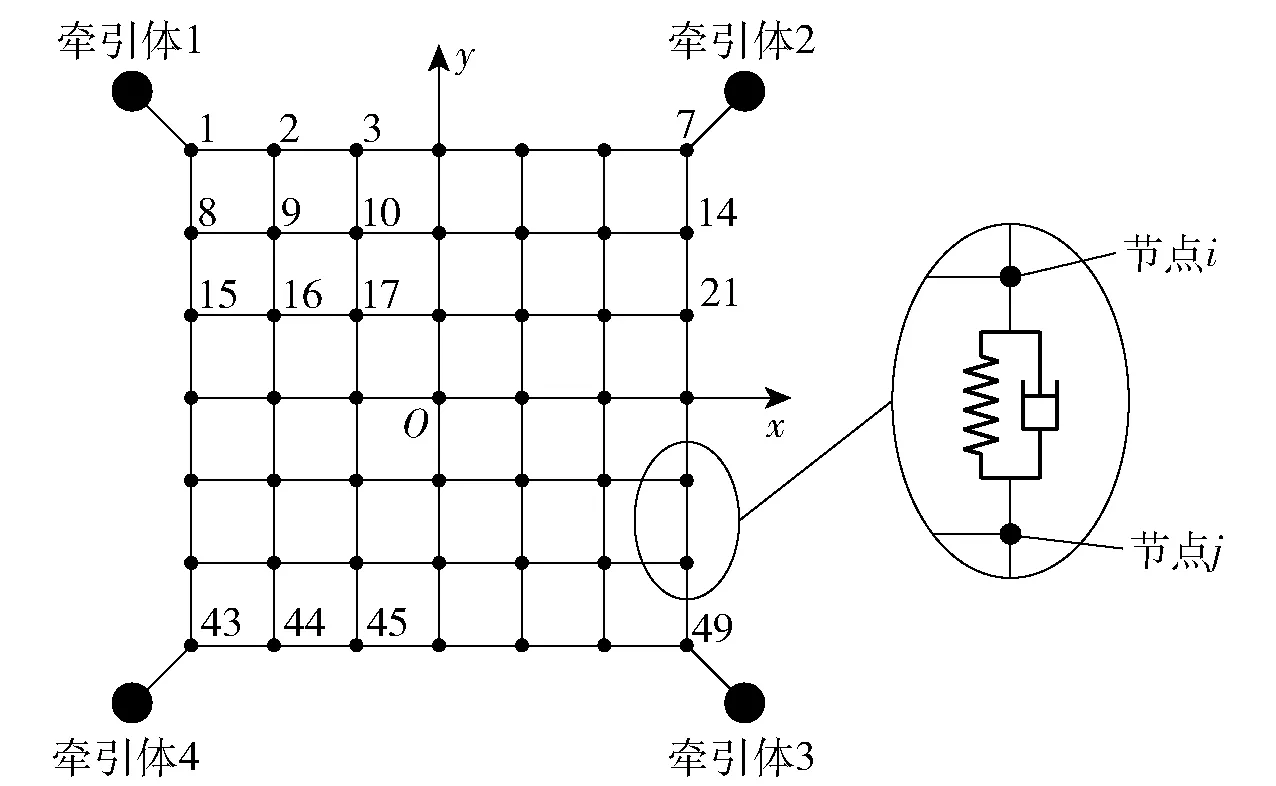
图1 绳网构型Fig.1 Configuration of tether-net
同时,为了便于描述绳网的拓扑结构及定位绳段,对绳网节点依次编号。引入0-1矩阵A表示绳网的拓扑结构,以aij表示矩阵的(i,j)元,矩阵的行数和列数与绳网总节点相同,在本文中为49. 若节点i与节点j之间通过绳段连接则记aij=1,否则记aij=0. 根据绳网节点的编号规律,A矩阵可以通过(1)式赋值:
(1)
式中:np表示绳网单侧边绳的物理节点数量,np=7;符号∨和∧是逻辑运算符号,分别表示“或”和“与”;符号|是整除符号,文中表示i能被np整除。可得本文中A矩阵的结构如图2所示。

图2 拓扑结构矩阵Fig.2 Topological structure matrix of tether-net
引入矩阵B表示节点间的绳段长度,bij代指矩阵的(i,j)元,B矩阵与A矩阵的结构相同。若节点i与节点j之间的绳段长度为l0,ij,则记bij=l0,ij;若节点i、j之间无绳段则记bij=0. 可知在图1所示的正方形网目的绳网中,其B矩阵的非0值均相等。
1.2 绳网动力学模型
本文使用弹簧质点模型对绳网进行建模,其基本原理是将绳网离散为有质量的质点和质点间无质量的弹簧、阻尼器单元。计算各质点的受力并建立相应的动力学方程,最后通过联立各个质点的动力学方程得到绳网的位移及受力情况。根据牛顿第二定律,图1中质点i的动力学方程为
(2)
式中:mi为质点i的等效质量,根据质点在绳网内的位置分布由(3)式定义:
(3)
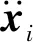
(4)
当绳段端点距离大于绳段原始长度时,绳段中产生拉力,否则不产生拉力,因此在以i、j为端点的绳段中,i点所受张力为
(5)
kij是网绳的等效刚度系数,
kij=EA/bij,
(6)
E是绳网选用材料的杨氏模量,A是网绳的横截面积,bij表示绳段的原始长度;lij是绳段的真实长度;eij是从i指向j的单位向量;vij是质点i与质点j的相对速度;dij是阻尼系数,
(7)
ζ为绳网选用材料的阻尼比。
2 基于遗传算法的绳网结构优化策略
2.1 绳网性能衡量指标
本文将绳网的展开面积定义为绳网4个网角所围成四边形的面积,将绳网的展开面积与设计面积的比值定义为展开率。绳网展开率的变化规律是评估绳网抓捕能力和确定绳网抓捕时机的重要因素。一般情况下,绳网的展开率越高,成功抓捕目标的概率越大,因此衡量绳网展开性能的衡量指标可以细化为:展开时间、展开位移、最大展开率、有效展开时间和有效展开位移,如图3所示。
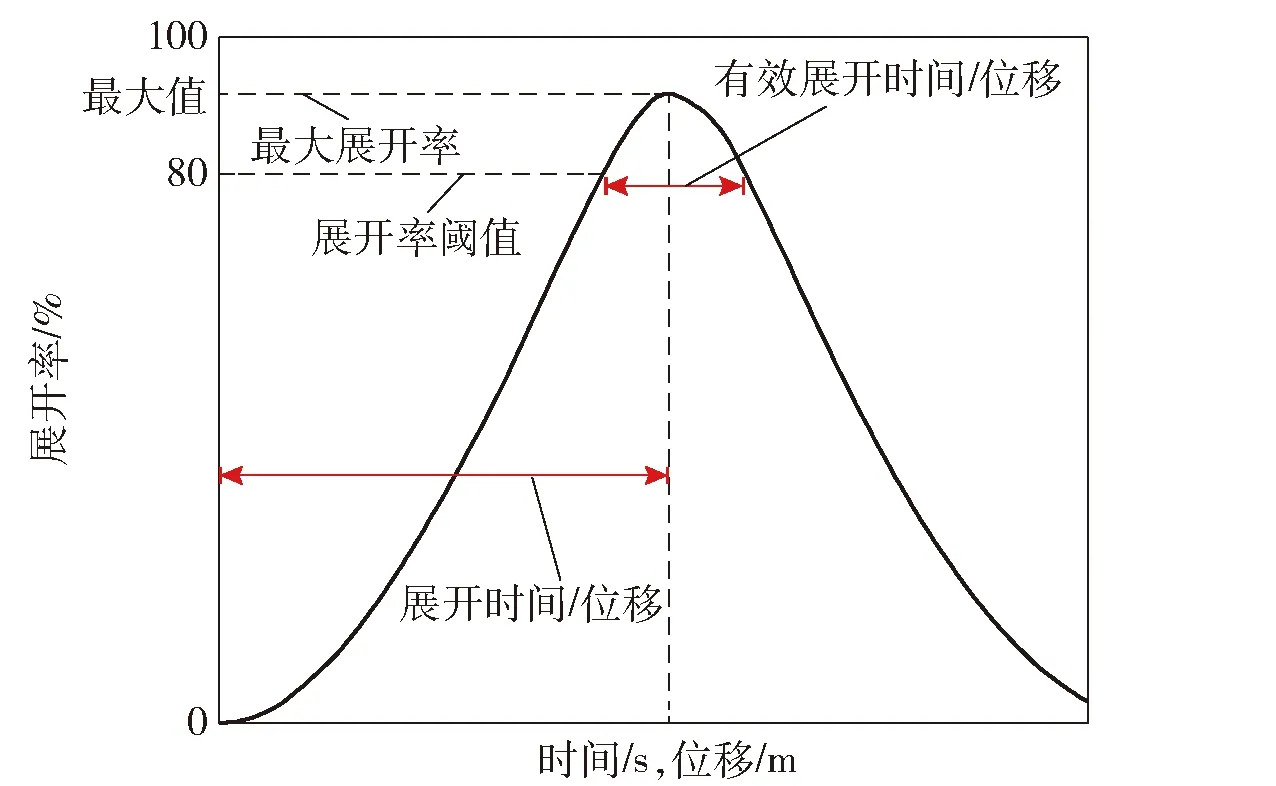
图3 展开性能指标Fig.3 Performance criteria of deployment
展开时间和展开位移可以通过发射速率和发射角度进行调整,为最佳抓捕时机的确定提供依据,因此在本文不作为性能指标。通常认为只要展开率超过设定的阈值,抓捕任务便可以完成,因此绳网最大展开率在本文中同样不做重点讨论。有效展开位移的大小表示绳网抓捕区间的覆盖范围。而相比有效展开位移,有效展开时间只能说明绳网展开率超过阈值的时间,对于抓捕成功评估意义不大。综上所述,选择有效展开位移作为本文的优化目标,并使用80%作为本文的展开率阈值。
2.2 绳网优化原理
空间绳网相关研究中,具有正方形网目的四边形绳网是应用最广泛的一种网型,而其他平面网型均是在此基础上的演变。本文以具有正方形网目的四边形绳网为研究对象对其网型结构进行优化,以提高绳网的有效展开位移。
不失一般性,本节使用4×4个网目的绳网举例,并将正方形绳网分解为3部分,如图4所示:第1部分是由牵引绳与牵引体组成;第2部分是多个同心的正方形边框,由首尾相连的闭环绳段组成,在图4中绳网边框的数量为2;第3部分是各个边框之间的连接线。本优化在保持绳网拓扑结构即总节点数的基础上,对绳网内部连接线的长度进行优化。为了保持绳网的正方形网型,在优化过程中,每个边框的整体外形尺寸不变。同时为了防止优化过程中因出现过大的网孔而降低绳网的包裹性能,各个边框之间的距离也保持固定。边框之间各连接线的长度将随着优化的进行而改变,相应构成边框的绳段长度将发生变化。同时,相比未优化的绳网,优化绳网B矩阵的非零元不再完全相等。最终将原本具有正方形网目的四边形绳网,优化为具有不规则四边形网目的绳网,并达到提高绳网有效展开位移的目标。虽然本文采用平面四边形绳网作为研究对象,但是其他构型绳网,如平面六边形和圆锥形等,均可按照本方法进行推广优化。

图4 绳网分解示意图Fig.4 Illustration of net structure
2.3 优化实现
空间绳网的中心对称性是其能够通过若干个牵引体同步牵引展开的原因之一。因此为了保持绳网各对称部分的展开同步性,只需优化相邻牵引体之间的单侧绳网结构,并将优化的结构以绳网中心点为基准进行N等份圆周阵列即可完成整个绳网的结构设计,如图5所示。其中N为牵引体数量,本文中N=4.

图5 绳网结构优化原理Fig.5 Optimization principle of net structure
遗传算法是一种模拟生物进化机制的全局优化算法,不需考虑所优化问题的内在工作原理,可以处理定义在离散、连续或混合搜索空间上的线性或非线性目标函数[30-31]。为了实现上述优化过程,引入了连接线落点系数pkq(k=1,2…,m,k为落点所在的边框序号,m为绳网的边框总数;q=1,2…,n,q为此边框落点的序号,n为边框k上的落点总数)来定位各个连接线在边框上的位置;并采用实数编码对落点系数进行编码,以各个落点系数为优化对象,以绳网有效展开位移为优化目标,对绳网结构进行优化。pkq的取值范围为[-1,1];pkq=-1时,连接点位于单侧边框的起点;pkq=1时,连接点位于单侧边框的终点。则在图5所示的坐标系中,可以得到连接点的坐标为
(8)
式中:lm为优化前绳网网目的边长;le,k为边框k的边长,连接线的长度可以通过连接点的坐标计算得到,进而得到优化后的B矩阵。对于任意给定的两个落点系数pka和pkb,其中a>b、k>1,必须保证pka (9) 式中:d为有效展开位移;a,b=1,2…,n.绳网边线网目划分数量为偶数时,所需要优化的落点系数数量为 Nump=1+2+…+(2m-1)=m2. (10) 为了验证提出方法的有效性,对结构优化后的绳网展开过程进行数值仿真。建立三维笛卡尔坐标系,将绳网收纳放置于坐标系原点O处,绳网的飞行方向为z轴正向。牵引体的发射速率10 m/s,发射角度40°,其中发射角度是牵引体的发射方向与绳网飞行方向(z轴)的夹角。本文算例在理想空间环境中进行,不考虑引力、摄动及空气阻力,所研究绳网的参数如表1所示。 表1 绳网参数Tab.1 Simulation parameters 本例中6网目绳网的边框数量为3,根据(10)式,需要优化的落点系数数量Nump=9.按照提出的绳网结构优化策略,使用Matlab编写了采用实数编码的遗传算法,初始种群规模为40,进化代数为100.约束阈值λe=λd=0.08,仿真时长设置为2 s.优化在CPU为Intel Core i7-6700HQ@2.60 GHz的笔记本电脑上进行,运算时间约为12 h 28 min.未优化及优化后的落点系数如表2所示。 表2 优化结果Tab.2 Optimization results 图6绘制了适应度函数(有效展开位移的负值)随进化代数的变化历程。随着进化代数的增加,适应度函数逐渐减小,最终收敛于-2.71 m,说明了优化策略的收敛性。 图6 适应度函数的迭代历程Fig.6 Optimization process of fitness function 图7绘制出了优化前及优化过程中绳网的构型,及该网形下绳网的有效展开率,图片截取于绳网展开率最大的时刻。从图7中可以发现,随着进化代数的增加,绳网的有效展开位移逐渐上升,绳网内部结构与未优化工况产生了较大差异。整个优化过程绳网保持了较好的中心对称性,连接点未出现重合且连接线未出现交叉。进化到第30代时绳网内部结构已经与最终优化结果十分接近,接下来的优化过程中有效展开位移最终收敛为2.71 m. 图7 优化网型图Fig.7 Optimized net structure 值得注意的是,优化前的连接线垂直于与其相连的边框,而优化后的连接线可能并不垂直于其连接的边框。这就导致了优化后的绳网需要更多的编织材料,同时绳网总质量也将增大。现有的研究表明绳网质量是影响绳网展开性能的因素之一[17,23],为了排除绳网质量增加对优化结果产生的干扰,引入了“质量等效”工况。在优化结果的基础上,降低网绳的密度使得其总质量与未优化绳网相同,通过对比未优化、优化和质量等效3种工况的展开历程,研究绳网结构优化后的质量增长对绳网展开性能的影响。首先列出了3种工况的质量参数,如表3所示。 表3 3种绳网的质量参数Tab.3 Mass parameters of different tether-nets 从表3中可以看出,优化后绳网总质量增加了约30.2 g,将优化后绳网的材料密度设置为870.4 kg/m3后使得绳网总质量与未优化时相同。进一步绘制出3种工况下展开率随时间和位移的变化曲线,如图8和图9所示。由图8和图9可看出:未优化绳网在约0.75 s时展开率首次达到80%的设定阈值,此时的展开位移为4.66 m;在约1.19 s时展开率再次达到80%,此时对应的位移为6.65 m.优化工况下绳网展开率分别在约0.76 s和1.38 s达到阈值,对应的展开位移分别为4.67 m和7.38 m.质量等效工况下绳网展开率分别在约0.75 s和1.34 s达到80%,对应的展开位移分别为4.66 m和7.34 m.可知未优化、优化和质量等效3种工况所对应的有效展开位移分别为1.99 m、2.71 m和2.68 m.绳网结构优化后,有效展开位移提高了约36.18%.尽管将质量等效后绳网的有效展开时间略微缩短,但是对于所关心的有效展开位移影响很小,提升率依然达到了34.67%。因此在下文中着重对比优化及未优化工况,不再对质量等效工况进行讨论。 图8 展开率的时间历程Fig.8 Time history of deployment rate 图9 展开率的位移历程Fig.9 Displacement history of deployment rate 未优化绳网分别在0.75 s和1.19 s达到设定展开率阈值80%,绘制了这两个时刻的绳网网型并与优化后的绳网进行对比,如表4所示。由表4可看出:0.75 s时两种工况的展开率很接近,绳网的状态也比较一致;主要差别体现在绳网网目的形态上,未优化绳网内部网目较为规则,而优化后的绳网网目大小不一。1.19 s时未优化绳网的展开率为80%,此时绳网中心出现了较为明显的回弹现象;而优化后的绳网中心出现了轻微回弹,且此时展开率约为93.8%,说明绳网结构优化减弱了绳网的回弹现象,提升了绳网的展开性能。 表4 优化前后网形对比Tab.4 Deployment sequences with and without optimization 为了研究结构优化策略提升绳网展开性能的原因,将空间绳网离散为牵引体及绳网本体两部分,利用二者质心随时间的变化过程描述绳网回弹现象,并通过有、无优化这两种工况的对比阐述结构优化策略的作用。图10给出了绳网本体与牵引体的质心追逐示意图,从中可看出:绳网展开过程中,牵引体首先拖动绳网展开,绳网本体质心Mn首先对牵引体质心Mb呈现追逐趋势;当绳网到达最大展开率附近时,Mn完成对Mb的追逐,两质心重合;此后绳网中心发生回弹,展开率逐渐下降,此过程中Mn在飞行方向上逐渐超越Mb. 图10 质心追逐示意图Fig.10 Chase of centers of mass 按照上述定义,绘制了两种工况下绳网本体和牵引体的质心位移历程,如图11所示。由图11可看出:由于两种工况下绳网最终均发生了回弹现象,因此,两种工况下绳网本体质心Mn对牵引体质心Mb均存在追逐现象。未优化工况下,两质心在约0.98 s时相遇,位移为5.62 m,相遇时间与图8中达到最大展开率的时间一致。优化工况下,两质心在约1.07 s时相遇,位移为5.98 m. 可知优化后的绳网将回弹开始时刻,即质心相遇时间推迟了0.09 s,将相遇位移延长了0.36 m. 图11 质心位移的时间历程Fig.11 Time history of displacement of centers of mass 进一步绘制了两种工况下质心的追逐速率,如图12所示。从图12可以看出,两种工况下质心的速率变化趋势接近。绳网本体质心Mn的速率先增大后减小,牵引体质心Mb的速率先减小、后增大。这是由于绳网发射时,牵引体具有一定的初始速度,在展开阶段初期其动能逐渐传递到绳网本体,发生回弹后,具有较高动能的绳网带动牵引体继续运动。值得注意的是,在Mb速率接近的情况下,优化工况下Mn速率最大值相比未优化工况降低了约16%。这说明采用优化结构的绳网降有效降低了绳网本体质心对牵引体质心的追逐速率,进而抑制了绳网回弹,提高了展开性能。 图12 质心速率的时间历程Fig.12 Time history of velocity of centers of mass 基于具有正方形网格的四边形平面绳网,在不改变绳网拓扑结构的前提下,本文通过优化网目结构提升绳网的展开性能。引入两种矩阵表示绳网的拓扑结构及绳段长度,使用弹簧质点法建立绳网的动力学模型。基于遗传算法提出了通过控制绳网连接线落点实现网目结构优化的策略。虽然本文采用平面四边形绳网作为研究对象,但是对于其他构型的绳网,如平面六边形和圆锥形等,均可按照本方法进行推广优化。通过数值仿真对比了绳网优化前后的结构及展开性能,并得到以下主要结论: 1)网目结构优化策略能够优化出满足抓捕需求的绳网,采用优化结构的绳网能够在几乎不影响最大展开率的前提下,将有效展开位移提高约36.18%。 2)网目结构优化策略会使绳网相比未优化时的质量略微增加,但是通过数值仿真发现这一变化对有效展开位移的干扰有限,可以忽略。 3)优化后的绳网降低了绳网本体质心对牵引体质心的追逐速度,抑制了绳网回弹,因此使得绳网的展开性能得到了提升。 本文提出的绳网结构优化策略没有改变绳网的拓扑结构,关于绳网拓扑结构的优化将是未来关注和研究的重点。 参考文献(References) [1] 余庆波,徐峰悦,王勤智,等.模拟卫星结构爆炸解体碎片分布特性[J].兵工学报,2014,35(7):1072-1076. YU Q B,XU F Y,WANG Q Z,et al.Explosion breakup debris distribution of simulated satellite [J].Acta Armamentarii,2014,35(7):1072-1076.(in Chinese) [2] NASA Orbital Debris Program Office.Satellite box score[J].Orbital Debris Quarterly News,2020,24(1):16. [3] YOSHIDA K,NAKANISHI H,UENO H,et al.Dynamics,control and impedance matching for robotic capture of a non-cooperative satellite[J].Advanced Robotics,2004,18(2):175-198. [4] REKLEITIS I,MARTIN E,ROULEAU G,et al.Autonomous capture of a tumbling satellite[J].Journal of Field Robotics,2007,24(4):275-296. [5] DEBUS T,DOUGHERTY S.Overview and performance of the front-end robotics enabling near-term demonstration (FREND) robotic arm[C]∥Proceedings of AIAA Infotech@Aerospace Conference.Seattle,WA,US:AIAA,2009. [6] 陈钦,杨乐平,张青斌.空间飞网发射动力学建模仿真研究与地面试验[J].国防科技大学学报,2009,31(3):16-19. CHEN Q,YANG L P,ZHANG Q B.Dynamic model and simulation of orbital net casting and ground test [J].Journal of National University of Defense Technology,2009,31(3):16-19.(in Chinese) [7] SHAN M,GUO J,GILL E.Review and comparison of active space debris capturing and removal methods[J].Progress in Aerospace Sciences,2016,80:18-32. [8] HUANG P F,ZHANG F,CHEN L,et al.A review of space tether in new applications[J].Nonlinear Dynamics,2018,94(5):1-19. [9] BOTTA E M,SHARF I,MISRA A K.Contact dynamics modeling and simulation of tether nets for space-debris capture [J].Journal of Guidance,Control,and Dynamics,2017,40(1):110-123. [10] MAO H N,SINN T,VASILE M,et al.Post-launch analysis of the deployment dynamics of a space web sounding rocket experiment[J].Acta Astronautica,2016,127:345-358. [12] FORSHAW J L,AGLIETTI G S,NAVARATHINAM N,et al.RemoveDEBRIS:An in-orbit active debris removal demonstration mission[J].Acta Astronautica,2016,127:448-463. [13] AXTHELM R,KLOTZ B,RETAT I,et al.Net capture mechanism for debris removal demonstration mission[C]∥Proceedings of the 7th European Conference on Space Debris.Darmstadt,Germany:ESA Space Debris Office,2017:18-21. [14] University of Surrey.Net successfully snares space debris[EB/OL].[2018-09-19].https:∥www.surrey.ac.uk/news/net-successfully-snares-space-debris. [15] BOTTA E M,SHARF I,MISRA A K.Contact dynamics modeling and simulation of tether nets for space-debris capture[J].Journal of Guidance,Control,and Dynamics,2017,40(1):110-123. [16] SI J Y,PANG Z J,DU Z H,et al.Dynamics modeling and simulation of self-collision of tether-net for space debris removal[J].Advances in Space Research,2019,64(9):1675-1687. [17] 于洋,宝音贺西,李俊峰,等.空间飞网抛射展开动力学建模与仿真[J].宇航学报,2010,31(5):1289-1296. YU Y,BAOYIN H X,LI J F,et al.Modeling and simulation of projecting deployment dynamics of space webs [J].Journal of Astronautics,2010,31(5):1289-1296.(in Chinese) [18] SHAN M H,GUO J,GILL E,et al.Validation of space net deployment modeling methods using parabolic flight experiment[J].Journal of Guidance,Control,and Dynamics,2017,40(12):3315-3323. [19] SHAN M H,GUO J,GILL E.Deployment dynamics of tethered-net for space debris removal[J].Acta Astronautica,2017,132:293-302. [20] 陈钦,杨乐平.空间绳网系统发射动力学问题研究[J].宇航学报,2009,30(5):1829-1833. CHEN Q,YANG L P.Research on casting dynamics of orbital net systems [J].Journal of Astronautics,2009,30(5):1829-1833.(in Chinese) [21] 李京阳,于洋,宝音贺西,等.空间飞网两种动力学模型的比较研究[J].力学学报,2011,43(3):542-550. LI J Y,YU Y,BAOYIN H X.Comparative study on two dyna-mics models of space net [J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(3):542-550.(in Chinese) [22] SALVI S.Flexible devices for active space debris removal:the net simulation tool [D].Milan,Italy:Polytechnic University of Milan,2014. [23] BOTTA E M,SHARF I,MISRA A K.Energy and momentum analysis of the deployment dynamics of nets in space[J].Acta Astronautica,2017,140:554-564. [24] 高庆玉,唐乾刚,张青斌,等.空间绳网二级发射模式动力学分析[J].兵工学报,2016,37(4):719-726. GAO Q Y,TANG Q G,ZHANG Q B.Dynamics analysis of a two-stage projection scheme of space nets system [J].Acta Armamentarii,2016,37(4):719-726.(in Chinese) [25] 陈青全,张青斌,唐乾刚,等.基于定力撕裂带的绳网网型控制研究[J].宇航学报,2018,39(12):1332-1339. CHEN Q Q,ZHANG Q B,TANG Q G,et al.Research on space net control based on fixed-force tear rope [J].Journal of Astronautics,2018,39(12):1332-1339.(in Chinese) [26] BOTTA E M,SHARF I,MISRA A K,et al.On the simulation of tether-nets for space debris capture with vortex dynamics[J].Acta Astronautica,2016,123:91-102. [27] ZHAI G,ZHANG J R.Space tether net system for debris capture and removal[C]∥Proceedings of 2012 4th International Conference on Intelligent Human-Machine Systems and Cybernetics.Nanchang,China:IEEE,2012:257-261. [28] BENVENUTO R,LAVAGNA M,SALVI S.Multibody dynamics driving GNC and system design in tethered nets for active debris removal[J].Advances in Space Research,2016,58(1):45-63. [29] LAPPAS V J,FORSHAW J L,VISAGIE L,et al.RemoveDEBRIS:an EU low cost demonstration mission to test ADR techno-logies[C]∥Proceedings of the 65th International Astronautical Congress.Toronto,Canada:International Astronautical Federation,2014. [30] GOLDBERG D E.Genetic algorithm in search,optimization,and machine learning [M].Boston,MA,US:Addison-Wesley Publishing Company,1989. [31] GEN M,CHENG R W.Genetic algorithms and engineering optimization [M].New York,NY,US:John Wiley and Sons,2000.3 仿真结果及讨论
3.1 优化结果


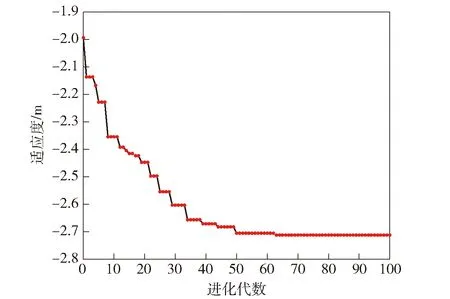

3.2 对比分析


4 结论
