冷却塔群塔干扰条件下脉动风压分布模式

赵 林，陈翰林，钱永丰，李敬生，葛耀君

(1. 同济大学 土木工程防灾国家重点实验室，上海 200092；2. 同济大学 桥梁结构抗风技术交通运输行业重点实验室，上海 200092；3. 中南安全环境技术研究院股份有限公司，武汉 430070；4. 中国电力工程顾问集团 东北电力设计院有限公司，长春 130021)

0 引 言

大型冷却塔作为一种空间薄壳结构，是火力发电厂与核电站广泛使用的工业建筑形式。近年来，随着我国电力事业的快速发展，冷却塔建设的需求不断攀升，很多冷却塔已经超过《超大型冷却塔设计导则》[1]190 m规范条款适用塔高的限制，冷却塔高度规模不断刷新纪录。随着高度的增加，塔筒空间结构质量轻、柔性大、阻尼小、自振频率低等特点趋于显著，使风荷载成为结构设计的控制荷载。另一方面，相关文献[2-3]指出干扰条件下冷却塔的荷载效应更加突出，现实工程中冷却塔数量从双塔、四塔向六塔、八塔逐渐发展，布置形式呈现矩形、菱形、一字形和L形等多样化，群塔干扰问题愈发突出，开展群塔干扰的研究工作显得尤为重要。

自1965年英国渡桥电厂冷却塔群（八塔组合）在五年一遇的中等强风条件下倒塌[2]，由此各国研究人员对冷却塔的群塔干扰效应问题进行了广泛的研究。国际上，Flaga等[4]研究了干扰引起的冷却塔表面荷载的准静态计算方法；Orlando[5]研究了双塔条件下冷却塔表面的平均风压分布模式；Niemann等[2]研究了双塔干扰并定义了内力层面的干扰系数。国内，顾志福等[6-8]研究了两塔和三塔干扰条件下的塔筒表面风压分布；赵林等[9-12]对干扰条件下的等效风荷载模式开展了相关的研究；柯世堂等[13-14]针对不同群塔布置条件下的干扰系数分布规律开展了相关研究；沈国辉等[15-16]研究了常见的双塔以及三塔布置情况下的冷却塔的升力系数以及内力响应的干扰变化规律；张军锋等[17-19]开展了群塔干扰条件下的冷却塔整体风荷载变化规律的研究。展艳艳[10]、于淼[11]分别针对六塔组合与八塔组合的冷却塔群体建筑进行了基于配筋包络的干扰准则的研究；王志男[20]、崔巍[21]研究了基于荷载分布模式的冷却塔优化选型算法。综合国内外研究现状，目前关于群塔干扰的研究大多集中于平均风荷载的干扰分布规律以及内力层面的干扰效应，少见对脉动风压的干扰效应开展系统深入的研究。实际中干扰不仅会影响平均风压的分布，也会对脉动风压产生显著的影响。关于脉动风荷载效应，周良茂等[22]通过现场实测结果说明了双塔布置条件下前塔的干扰会对后塔表面的脉动风压产生显著放大；顾志福等[8]在利用风洞试验对双塔风荷载的相互干扰的研究中指出塔群的干扰除了关注平均风压的变化外，需要更加重视干扰引起的脉动风压的变化。基于实测与试验所得到的冷却塔表面脉动风压受干扰影响较大的事实引起了国内外部分学者的重视，并针对不同干扰条件下的脉动风压分布规律开展了相关实测与试验研究。表1列举了部分研究者在冷却塔表面脉动荷载分布以及受干扰的影响方面的研究历程。

从各国学者对冷却塔脉动风荷载的研究现状看，传统的对冷却塔的脉动风荷载干扰效应的研究以定性描述为主，缺乏定量的评价指标，对脉动风荷载的干扰效应开展定量的研究具有重要的工程意义。已有的对冷却塔表面的脉动风荷载的量化研究仅围绕单塔开展[30-31]，而针对群塔组合条件下的脉动风荷载干扰效应的量化研究未充分开展。实际工程中在考虑冷却塔的风荷载时需要对冷却塔表面的平均风压以及脉动风压的分布模式进行量化表达，现有的研究中关于平均风荷载的干扰分布模式的量化研究较为成熟，而脉动风荷载的干扰分布模式的量化研究相对滞后。鉴于此，开展了冷却塔风致干扰脉动荷载效应研究。以某一在建的八塔组合冷却塔项目为背景，选取常见的矩形布置方式，在风洞进行刚体模型测压试验，得到模型表面的风压分布时程；对冷却塔干扰后的脉动风压分布模式进行量化表达。

1 同步测压风洞试验

依托冷却塔工程为八塔组合矩形布置，塔高185 m，零米直径126.8 m，出口直径82.5 m，喉部直径79.2 m。表2列举了塔筒的实际几何外形与尺寸参数。为降低表面风荷载，本工程冷却塔为带肋塔结构形式。测压风洞试验是在同济大学TJ-3风洞中完成的，该风洞是一个竖向布置的闭口回流式边界层风洞，封闭试验段长14 m、宽15 m、高2 m，风速范围为1～17.6 m/s，连续可调，流场不均匀性指标δU/U≤1.9%，湍流度Iu≤2.0%，来流竖向倾角-0.2°≤Δα≤+0.2°，水平偏角-0.1°≤Δβ≤+0.1°。

表2 冷却塔塔筒实际尺寸参数Table 2 Size parameters of the cooling tower

试验采用1∶300缩尺比制作冷却塔刚性内外压同步测试模型，单个结构迎风面积约为0.18 m2，八塔群塔组合后阻塞度约为2.4%。为了保证模型在试验风速下不发生变形和显著的振动，并方便布置内外压测点，采用中空双层有机玻璃制作模型。测点沿着外表面布置12层，每层36个测点沿着环向均匀布置，图1展示了测点的布置示意图。试验采用同步扫面测压技术，测压信号采样频率为300 Hz，每个测点采样时长为60 s，其采样精度满足实际工程的要求。

图1 模型测压孔布置示意图Fig. 1 Schematic diagram of the model pressure tap layout

图2 群塔组合布置形式Fig. 2 Grouped-tower arrangement

试验中八塔组合采用矩形布置，图2展示了八塔在风洞中的布置方式，其中L为相邻塔筒之间的距离，D为塔筒直径，每种布置形式下相邻塔中心间距为1.5倍的冷却塔底部直径。图2定义了风向角的正方向—以x轴为0°起点，正对来流方向，从x轴开始沿着来流顺时针旋转为正角度的方向。风向角沿着环向从0°～360°变化，每间隔22.5°进行一次测压试验。为了减少试验的工作量，根据矩形布置形式的对称性，只需对1号塔和2号塔进行测压试验。共获得了1号塔和2号塔的各16个风向角下塔筒表面的风压时程。图2中的粗糙元与尖劈用于模拟实际环境中的B类风场，其在风洞试验中的布置如图3所示。

图3 B类流场布置图Fig. 3 Configuration of the type B flow field

试验模拟B类湍流场，其风剖面特性见图4。试验的平均风速与湍流度同规范（JTG/T3360-01-2018）吻合良好，脉动风压与中国规范（JTG/T3360-01-2018）相比偏高，但与日本规范（AIJ-RLB-2004）相比偏低，且其对试验中干扰效应的整体规律不产生影响。图5是试验风场的顺风向和横风向的风速功率谱函数，与规范建议的实测风谱拟合对比良好，表明试验采用的流场能够较好地再现真实风谱。

图4 B类湍流场的风剖面特性Fig. 4 Wind profiles of the type B turbulent flow field

图5 B类湍流场风谱特性Fig. 5 Wind spectra of the type B turbulent flow field

实际原型冷却塔处于超高临界雷诺数状态，现有边界层风洞试验过程无法满足雷诺数相似比。为了模拟实际冷却塔表面超高雷诺数效应下的流场分布，试验采用在冷却塔表面粘贴具有一定厚度的粗糙纸带来模拟实际冷却塔表面的肋条以及补偿雷诺数效应。粗糙纸带沿着塔筒环向均匀分布，整个塔筒外表面环向共粘贴36条子午向通长纸带。图6展示了雷诺数效应的模拟情况，其中平均风压与规范吻合较好，表明粘贴粗糙纸带的模拟方式达到了预期效果。脉动风压的模拟结果与实测结果趋势分布亦较为吻合，其分布介于不同学者实测结果之间。基于风剖面、风谱函数以及雷诺数荷载效应均符合实际工程的精度要求，在此基础上开展脉动风荷载的干扰效应研究。

2 脉动风压干扰分布特性

2.1 脉动风压干扰分布特性

群塔组合后干扰风压的分布十分复杂，需要分门别类加以探讨。赵林等[20,32]针对典型的矩形布置和菱形布置条件下的冷却塔干扰平均风荷载模式进行研究，将复杂的干扰风压分布归纳为三种典型的风荷载模式：“对称风压”、“侧向非对称风压”和“通道风压”。其认为来流的方向不同，塔群的组合布置对特定塔筒的风压分布的影响不同，形成如“遮挡效应”、“夹道效应”等气流干扰效应，从而改变单个塔筒表面的风压分布。脉动风压与平均风压紧密联系，推测脉动风压的分布随着风向角的变化亦具有分区的特性。

图6 模型表面静态压力和动态压力雷诺数效应模拟Fig. 6 Reynolds number effect simulations of the static and dynamic pressures on the model surface

以2号塔筒为研究对象，将来流方向分为如图7所示的三类。第一类如图7（a）所示，来流正对2号塔筒，称为迎风来流，以0°风向角为例来说明迎风来流下的脉动风压分布，图8（a）是2号塔喉部位置的脉动风压环向分布示意图。脉动风压沿着环向分布较为对称，在迎风点两侧90°左右区域有小幅度的波峰，整体分布与单塔类似，呈现“V”型分布，脉动风压的峰值在0.1～0.25之间波动，与单塔接近，表明在对应风向角下干扰对脉动风压的放大作用较弱，而这种影响也不同于相同工况下平均风压在背风区分布受干扰效应影响显著的变化趋势[17,33]。图7（a）流场图解释了“V”型分布的成因，当风从2号塔迎风侧以小角度吹过来时，2号塔周边的塔对其流场影响较小，表现为2号塔表面环向脉动风压受干扰影响较小，作为与其他干扰效应的区别，本文定义这种类型的干扰效应为“弱干扰”效应。当来流风的角度较小或者其角度不至于造成前塔对后塔遮挡作用很强时，受干扰的塔表面脉动风压多呈现“V”型分布，不同角度下1号、2号塔的“V”型分布情况如图9（a）所示。矩形布置的对称性使得呈现“V”型分布对应的风向角较多。

图7 脉动风压干扰效应的流场示意图Fig. 7 Schematic diagram of the fluctuating wind pressure interference effect

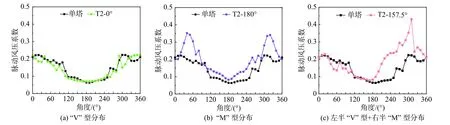
图8 典型脉动风压分布类型Fig. 8 Typical distributions of the fluctuating wind pressure

图9 不同风向角下脉动风压的分布模式分类Fig. 9 Classification of the fluctuating wind pressure distribution patterns under different wind direction angles

另一种来流方向使2号塔处于完全背风的位置，如图7（b）所示，称这种来流方向为背风来流，典型的风向角为180°。此时2号塔表面喉部位置的脉动风压分布如图8（b）所示，0°～180°范围内脉动风压沿着环向呈现典型的“M”型分布模式。从图7（b）流场图分析，当研究塔筒处于背风侧的时候，其处于前塔的尾流区，且其两侧与周边塔筒形成通道使得气流具有加速效应，受扰塔在尾流与通道加速的气流组合作用下表现出在迎风点两侧30°～90°范围内的脉动风压显著放大，当受扰塔两侧通道相对来流方向较为对称时，其脉动风压的分布将出现近似“M”型分布。当风向角偏离180°但具备类似的流场特征时，其干扰效应均会使得受扰塔表面的脉动风压形成近似的“M”型分布模式。不同风向角下的“M”型分布的脉动风压如图9（b）所示。其干扰放大幅度较大，脉动风压在0.1～0.5之间波动，表现出强干扰的特征，整体呈现出脉动效应沿环向整体放大的趋势，放大倍数介于0.95～1.8之间，亦不同于类似布置工况下游冷却塔表面风平压均呈现压力系数降低的效应[20-21]。结合脉动风压分布仍呈现较为对称的特点，称这种对称的大幅度干扰效应为“对称强干扰”效应。

第三种来流模式如图7（c）所示，当风向角处于某些特殊的位置时，流场会在受扰塔的迎风点的一侧形成遮挡，另一侧形成加速，使得脉动风压呈现较强的非对称分布的特点，表现出加速侧脉动风压相比单塔急剧放大，遮挡一侧的脉动风压相比单塔减小，形成典型的半“V”型+半“M”型分布模式。选取风向角为157.5°条件下的2号塔为研究对象，其所处流场的示意图如图7（c）所示，2号塔迎风点右侧的流场处于加速侧，其脉动风压显著放大，而迎风点左侧的脉动风压因处于前塔遮挡区域表现出减小的特点，喉部位置的风压在不对称的流场中形成如图8（c）所示的半“V”型+半“M”型分布特点。脉动风压系数分布从0.1～0.45波动，表现出较强的干扰效应。由于流场的不对称性其迎风点右侧出现大幅放大，左侧则与单塔相比差别较小。将这种特殊角度下的干扰效应称为“非对称强干扰”效应。1号、2号塔表面的脉动风压呈现半“V”型+半“M”型分布的角度如图9（c）与图9（d）所示。相比于前面两种分布模式，半“V”型+半“M”型分布的角度很少，表明大部分来流方向经过扰流干扰后依然保持对称性，仅少数来流方向会形成不对称流场。

2.2 脉动风压干扰分布曲线拟合探讨

三种来流模式下脉动风压的干扰效应与来流风向角度以及风压所在环向位置密切相关。为了更清晰地把握脉动风压干扰分布的规律，尝试对脉动风压的干扰分布模式进行量化表达。目前对于干扰后冷却塔表面平均风压的分布曲线的拟合研究较多，对群塔组合条件下塔筒表面的脉动风压分布拟合研究涉及较少。规范[1,34]中提出了单塔平均风压拟合公式，赵林[17]提出了平均风压干扰分布拟合曲线，相关文献均采用类似式（1）所示形式：

式中Cp(θ) 表示平均风压，θ 表示冷却塔沿着环向的角度，取m=7，ak表示拟合系数。式（1）较好地体现了平均风压沿着环向对称分布的特点。考虑到干扰后脉动风压的环向分布不再对称，在利用式（1）进行脉动风压的干扰分布刻画之前，有必要针对式（1）进行改进。本文在保留三角函数项的基础上，在循环变量整数k前面引入修正系数v，并将纯余弦表达式的组合改为由四项式余弦加四项式正弦和拟合常数项组成的九项式，此时m= 4。具体表达式如式（2）所示：

式中：c为拟合常数项；ak、bk为拟合系数；v为修正系数，经试验后取为0.9；θT为研究位置的环向角度；k为循环变量。根据矩形布置的对称性，选择1号、2号塔筒为拟合对象。针对每种塔在16个试验风向角下的分布模式开展拟合。为直观反映不同风向角下的脉动风压的拟合效果，将1号、2号塔的拟合效果按照风向角对应排列，如图10所示。可见采用式（2）对脉动风压的分布进行拟合效果较好。且随着风向角的变化，脉动风压的分布模式的变化较大。可见脉动风压的分布模式依赖于特定的风向角。

脉动风压不同的分布模式使脉动风压沿塔筒环向分布存在明显差异，为方便工程设计，对脉动风压按照分布模式推荐拟合曲线显得必要。图11给出了四种分布模式下塔筒的推荐拟合曲线的上下限，并在表5给出了上下限曲线的拟合参数。

图10 不同风向角下塔筒表面喉部位置的脉动风压拟合情况Fig. 10 Data fitting of the fluctuating wind pressure at the throat of the tower surface under different wind direction angles

图11 脉动风压分布模式分类拟合Fig. 11 Fitting classification of the fluctuating wind pressure distribution patterns

表3 脉动风压拟合参数（1号塔）Table 3 Fitting parameters of the fluctuating wind pressure for tower 1

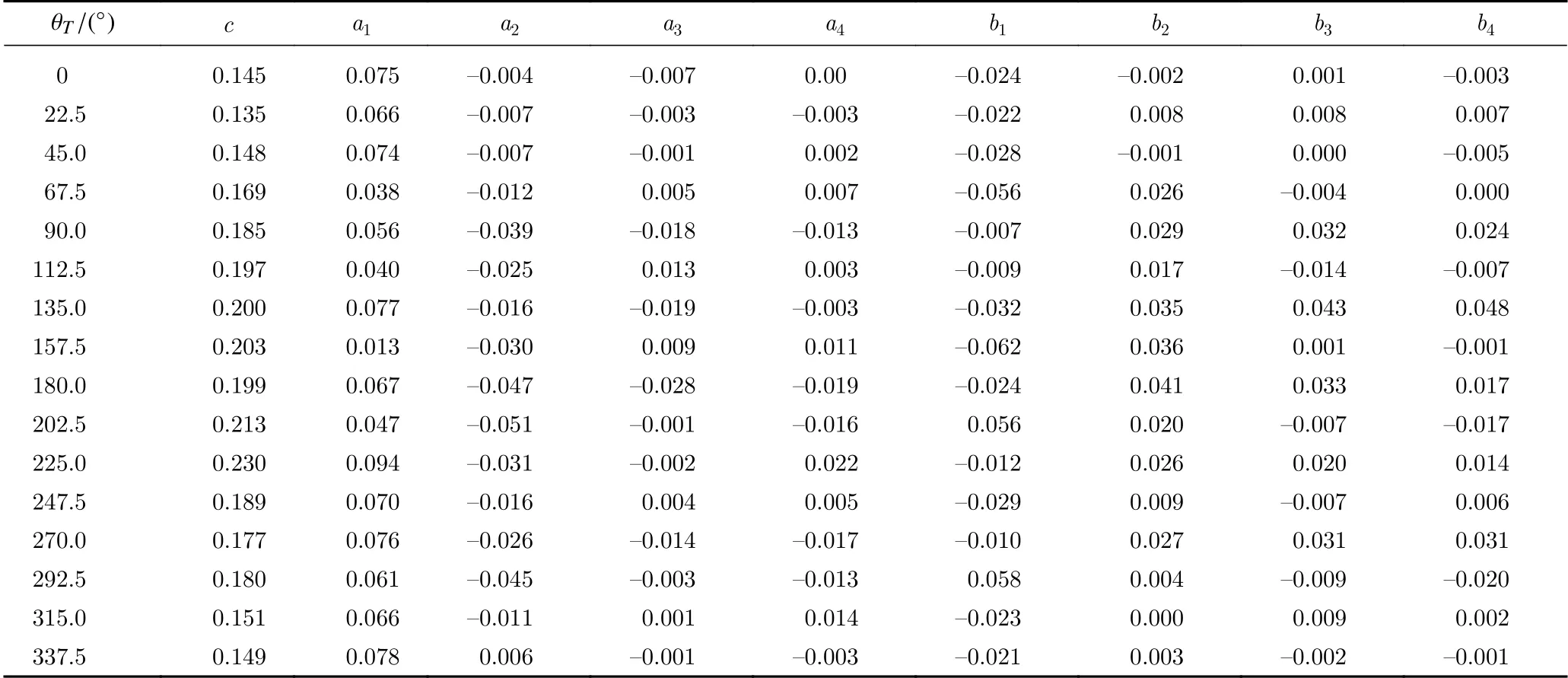
表4 脉动风压拟合参数（2号塔）Table 4 Fitting parameters of the fluctuating wind pressure for tower 2

表5 不同脉动风压分布模式的推荐拟合公式Table 5 Recommended fitting formulas for different fluctuating wind pressure distribution patterns

3 结 论

基于B类地貌，八塔矩形布置条件下的风洞试验，进行了三种来流模式下脉动风压干扰分布特性的对比研究，探讨了脉动风压的分布模式的分类与形成机理，并在前人研究基础上提出了脉动风压干扰分布拟合公式。通过考虑不同风向角的结果的对比，获取了脉动风荷载的基本干扰特性，得到以下基本结论：

1） 脉动风压的干扰分布模式有三类：“V”型、“M”型、半“V”型+半“M”型分布。“V”型分布模式由“弱干扰”效应形成，“M”型分布模式由“对称强干扰”效应形成，半“V”型+半“M”型分布模式由“非对称强干扰”效应形成。

2） 脉动风压干扰分布模式建议采用四项式余弦加四项式正弦和拟合常数项组成的九项式拟合，拟合参数的取值依赖于风向角的变化。推荐了四种分布模式下的脉动风压表达式，并给出了其拟合参数的上下限值。

3） 本文基于风洞试验这一传统的研究方式对脉动风压进行干扰研究，创新地提出结合来流特点利用数形结合的方式将脉动风压分类加以定量描述，实现了从原理到现象的全过程描述。本文关于脉动风压干扰的研究策略和结论可为类似群体建筑物/构筑物组合气动干扰效应分析提供借鉴思路。

4） 本文仅仅针对八塔矩形布置和1.5倍塔底直径的塔间距条件下的脉动风压分布模式以及其干扰机理进行了研究，对其他形式的布置（如菱形）以及塔间距变化过程中的脉动风压分布情况，需要进一步加以研究探索。