基于改进的k-ω-γ转捩模式预测高超声速飞行器气动特性

王 亮，周 玲

(1. 水利部农村电气化研究所，杭州 310012；2. 北京理工大学，北京 100081)

0 引 言

边界层转捩的准确预测对高超声速飞行器至关重要，它对飞行器的气动力/热、发动机性能、飞行器操作系统等有着重要的影响。2017年，周恒和张涵信[1]撰文提出了有关近空间高超声速飞行器边界层转捩和湍流的两个问题，其中针对转捩方面的研究，指出“为增强对高超声速飞行器边界层转捩预测的能力，需要开展哪些方面的研究工作及其困难”。同一年，陈坚强等[2]对高超声速边界层转捩研究现状及发展趋势进行了系统的介绍，包括高超声速边界层转捩影响因素研究、转捩机理研究、转捩预测方法及模型研究、促进/推迟转捩的控制方法研究以及一些公开的飞行试验等方面的进展。之后，杨武兵等[3]针对高超声速边界层转捩问题、转捩的多种研究方法现状及发展趋势进行了综述。刘向宏等[4]则对高超声速边界层转捩实验方面进行了综述，并对未来的实验研究给出了建议。此外，董昊等人[5]针对粗糙元对高超声速边界层转捩的影响进行了总结。

近几年，国内外对高超声速边界层转捩问题的研究主要集中在风洞实验以及高精度数值模拟方面。Yao等[6]在马赫数6静音风洞中研究了平板三角翼的边界层转捩情况，分析了攻角和雷诺数对转捩起始位置的影响。Dong等[7]采用直接数值模拟和油膜干涉技术，研究了马赫数为5时粗糙元引起的高超声速边界层转捩物理机制。Steelant等[8]对一细长体高超声速外形进行了数值和实验研究，用于分析该飞行器在弹道点的转捩问题。Kostak等[9]针对美国空军科学研究室的边界层转捩飞行试验外形进行了关于自由来流扰动影响的实验研究，不同风洞实验以及CFD研究分析结果在飞行器表面加热、驻涡条带以及模态增长方面得到了一致的结果。Zhang等[10]在北京大学马赫数6.5风洞中研究了平板边界层转捩的演化过程。Zhao等[11]采用基于当地拟合的转捩模型和线性稳定性分析研究了自由来流总温对高超声速边界层转捩的影响规律。韩宇峰等[12]采用数值方法分析了高超声速三维边界层定常横流涡的演化机制。

在转捩模式研究方面，从20世纪90年代起，文献公开发表的转捩模式已经多达十几种。其中比较著名的有基于当地变量的γ-Reθt模式[13-14]，适用于叶轮机高来流湍流度的KT-KL-ω模式[15-16]，适用于高超声速边界层转捩预测的k-ω-γ转捩模式[17-19]，等等。然而，由于边界层转捩问题的复杂性，不同流动和物形条件下转捩机制差异较大，目前几乎所有的转捩模式均不具有普适性。并且，针对工程复杂外形，由于其同时存在多种转捩机制，且转捩阵面难以准确捕捉，因此，目前关于转捩模式应用于工程复杂外形，特别是高超声速流动中复杂外形的研究较少。

近几年来，Zhou等[20-21]对k-ω-γ转捩模式进行了改进。改进的k-ω-γ转捩模式采用网格预处理技术，可以快速大规模并行获取具有非当地变量属性的边界层参数，并同时考虑了横流转捩，因此该改进的k-ω-γ转捩模式具有推广至工程复杂外形应用的潜力。并且，Zhou等在文献[21-22]实现了改进的k-ω-γ转捩模式对X-33、X-51A飞行器前体以及类X-51A飞行器全机的边界层转捩预测。

本文在文献[22]的研究基础上，进一步采用改进的k-ω-γ转捩模式对类X-51A飞行器全机进行不同攻角、雷诺数条件下的边界层转捩预测，分析其气动力和进气道性能，为类似的工程应用提供参考。

1 物理模型

选用参考X-51A飞行器[23]巡航体部分进行气动外形优化设计后的类X-51A飞行器作为研究对象，优化后的类X-51A飞行器如图1所示。该飞行器总长L= 4 270 mm，全机宽880 mm，高460 mm，前体压缩面采用两级压缩，后体下壁板一直延伸到飞行器尾部，质心位置为x= 0.7L，y= 0.15L，z= 0。飞行器的设计巡航状态为Ma∞= 6，α= 4°。

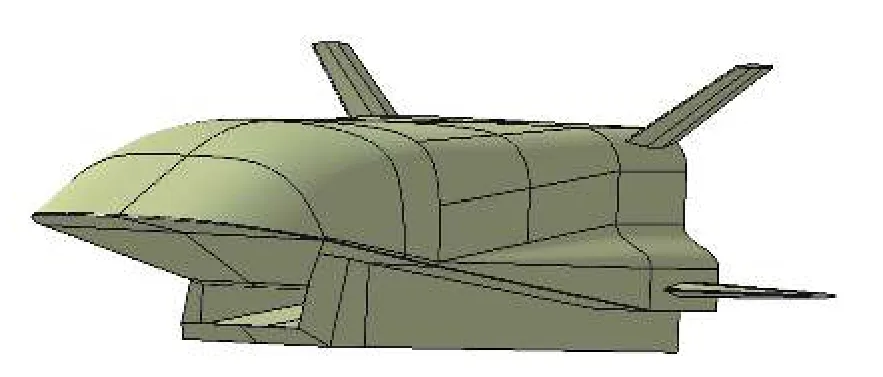
图1 气动优化设计后的类X-51A飞行器全机外形示意图Fig. 1 Configuration of X-51A-like full vehicle after aerodynamic optimization design

2 计算方法

2.1 控制方程

本文选取半离散的有限体积方法求解RANS方程组。层流N-S方程和湍流、转捩输运方程采用统一的离散方式：无黏通量采用差分分裂的Roe格式，网格界面上采用MUSCL（Monotone Upstream-centered Schemes for Conservation Laws）格式插值获得高阶精度；黏性项采用二阶中心差分格式进行离散；时间推进采用计算稳定性好、对时间步长约束小的隐式LU-SGS（Lower-Upper Symmetric Gauss-Seidel）格式。转捩模型采用改进的k-ω-γ转捩模式，该模式的具体介绍参考文献[20-22]。

2.2 计算网格和边界条件

计算采用半模多区对接结构网格，类X-51A飞行器头部和尾翼采用O型拓扑对接，前体压缩拐角、内流道和边界层内等局部流动变化较大的区域网格加密并光滑过渡，半模网格总量约为1 300万。针对该类X-51A飞行器，作者已经在发表的文献[22]中进行了X-51A飞行器前体网格无关性验证，采用的改进k-ω-γ模式预测的前体转捩区域与风洞实验结果吻合较好；并且在文献[22]中预测的类X-51A飞行器全机转捩区域与Reθ/Mae转捩准则预测结果较为吻合。因此，本文直接采用文献[22]验证后的类X-51A飞行器全机网格分布以及相关计算参数进行计算。关于网格无关性以及计算可靠性的相关验证细节可参考文献[22]。

为了研究边界层转捩对类X-51A飞行器全机气动力特性的影响，参考X-51A飞行器的设计任务剖面和类X-51A飞行器的设计巡航状态，将计算高度范围定义在H= 20 ～ 27 km，飞行马赫数范围定义在Ma∞= 5～7，飞行攻角范围定义在α= 0°～4°，研究不同攻角和雷诺数对飞行器边界层转捩的影响规律，以及边界层转捩对飞行器气动力和进气道性能的影响规律。具体计算工况如表1所示，高空来流湍流度取Tu∞= 0.1%，飞行器壁面温度设置为Tw= 400 K。所有工况均采用全层流、改进的k-ω-γ转捩模式和SST湍流模式三种方法进行计算。

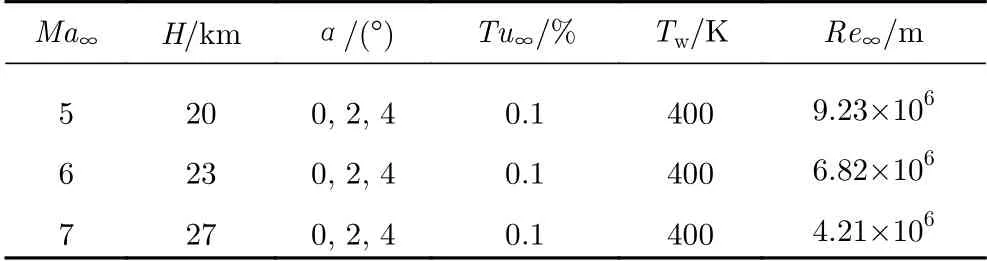
表1 类X-51A飞行器计算工况Table 1 Computation conditions for the X-51A-like vehicle

3 攻角和雷诺数对边界层转捩的影响

图2给出了不同攻角、雷诺数条件下采用改进的k-ω-γ转捩模式计算得到的类X-51A飞行器全机壁面和进气道的间歇因子γ的分布，γ= 0的区域表示全层流区域，0 ＜γ＜ 1的区域表示转捩区域，γ≥ 1的区域表示全湍流区域。

可以看到，相同雷诺数条件下，随着攻角从0°增大到2°、4°，类X-51A飞行器背风面转捩起始位置向上游移动显著。以Ma∞= 5、Re∞= 9.23×106/m工况为例，如图3所示，随着攻角增大，飞行器背风面流动汇聚线逐渐向上游移动，导致汇聚线下游的横向流动更加显著，横流效应增强。与之对应，飞行器背风面的间歇因子分布也随着横流区的发展逐渐向上游和中心线区域扩张。飞行器侧面转捩起始位置受攻角影响较小，所有攻角条件下均为全湍流状态。飞行器前体压缩面，Re∞= 9.23×106/m、6.82×106/m条件下，转捩起始位置均在压缩拐角处，随攻角变化较小。Re∞=4.21×106/m条件下，转捩起始位置延迟到进气道唇口反射激波与进气道上壁面边界层干扰产生的分离泡位置处，转捩起始位置随攻角的变化趋势与反射激波与边界层干扰位置的变化趋势一致：随着攻角增大，转捩起始位置略向上游移动，但变化幅度很小，如图4所示。进气道下壁面，随着攻角增大，转捩起始位置逐渐向上游移动。以Ma∞= 7、Re∞= 4.21×106/m条件为例，如图5所示，α= 0°工况下，进气道下壁面中心线附近，转捩起始位置在第二道反射激波与下壁面边界层干扰产生的分离泡位置处。随着攻角增大到2°和4°，进气道下壁面中心线附近转捩起始位置逐渐提前到反射激波与边界层相交位置之前，并抑制了激波/边界层干扰产生的分离。进气道上、下壁面靠近侧缘区域，受侧壁的影响，转捩起始位置均从唇口处发展起来，几乎不受攻角变化的影响。而进气道侧面，由于转捩起始位置在反射激波后，因此，随着攻角增大，激波反射角小幅增大，侧面转捩起始位置小幅提前。

相同攻角条件下，马赫数、高度变化导致来流雷诺数变化，进而对类X-51A飞行器边界层转捩产生影响。随着马赫数从5增大到6、7，飞行高度从20 km增加到23 km、27 km，自由来流雷诺数从9.23×106/m逐渐降低到6.82×106/m、4.21×106/m，类X-51A飞行器背风面转捩起始位置逐渐延迟，且攻角越小，延迟效应越显著。飞行器侧面转捩起始位置受雷诺数影响较小，所有雷诺数条件下均为全湍流状态。飞行器前体压缩面，随着来流雷诺数降低，转捩起始位置逐渐从压缩面拐角处延迟到进气道上壁面反射激波与边界层干扰产生的分离泡位置处。Re∞= 9.23×106/m条件下，迎风面转捩起始位置在进气道唇口附近，中心线区域相对靠后。随着Re∞减小到6.82×106/m、4.21×106/m，迎风面转捩起始位置延迟到流动向中心线汇聚的区域，如图2和图6所示。进气道下壁面和侧面，随着来流雷诺数降低，转捩起始位置同样有一定范围的延迟。

图2 不同攻角和雷诺数条件下类X-51A飞行器壁面间歇因子分布Fig. 2 Intermittent factor distributions on the surface of X-51A-like vehicle at different angles of attack and Reynolds numbers

4 边界层转捩对气动力的影响

边界层转捩对飞行器气动性能影响显著，这里在已获得的层流、转捩和湍流的计算结果基础之上分析边界层转捩对类X-51A飞行器气动力特性的影响。主要通过升力系数CL、阻力系数CD、升阻比L/D和俯仰力矩系数Cm来评估飞行器的气动力特性，这些气动参数定义如下：

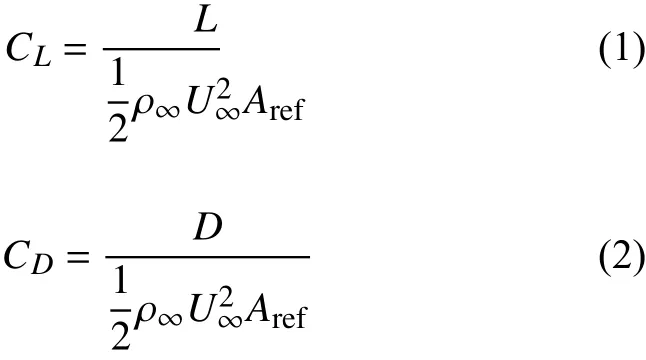
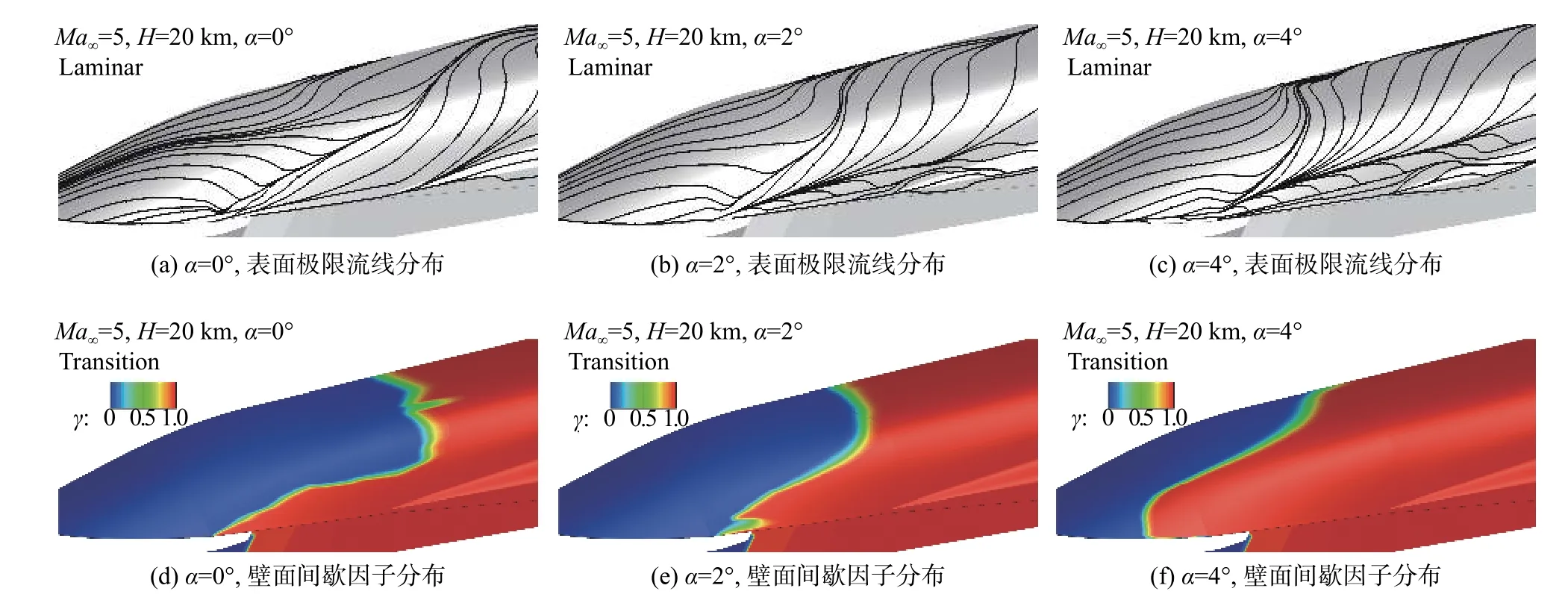
图3 不同攻角条件下类X-51A飞行器背风面表面极限流线和壁面间歇因子分布（Ma∞ = 5，Re∞ = 9.23×106/m）Fig. 3 Limit streamlines and intermittent factor distributions on the leeward side of the X-51A-like vehicle at different angles of attack(Ma∞ = 5, Re∞ = 9.23×106/m)

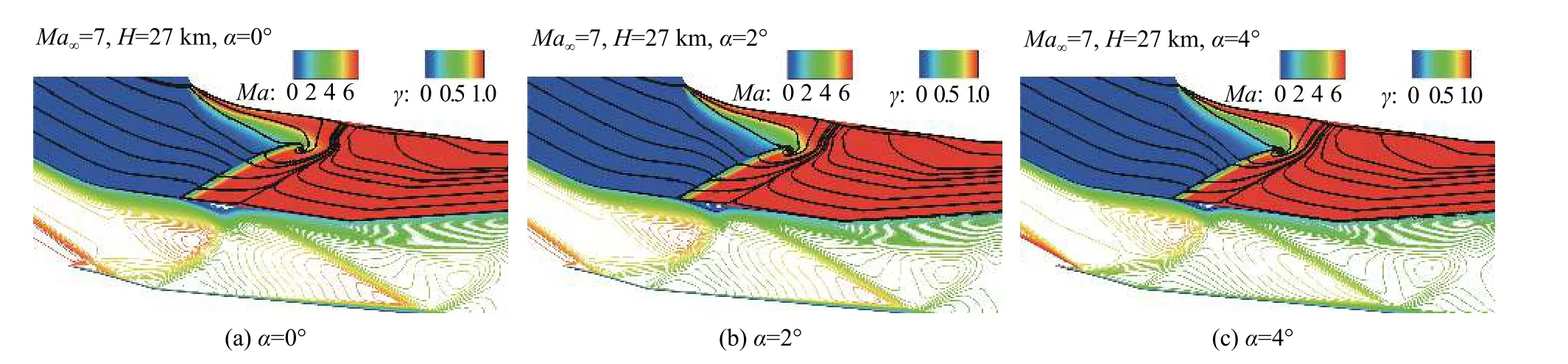
图4 不同攻角条件下类X-51A飞行器进气道对称面等马赫线分布以及进气道上壁面间歇因子和表面极限流线分布（Ma∞ = 7，Re∞ = 4.21×106/m）Fig. 4 Mach number distributions in the symmetrical plane, limit streamlines and intermittent factor distributions on the upper wall of the X-51A-like vehicle inlet at different angles of attack (Ma∞ = 7, Re∞ = 4.21×106/m)

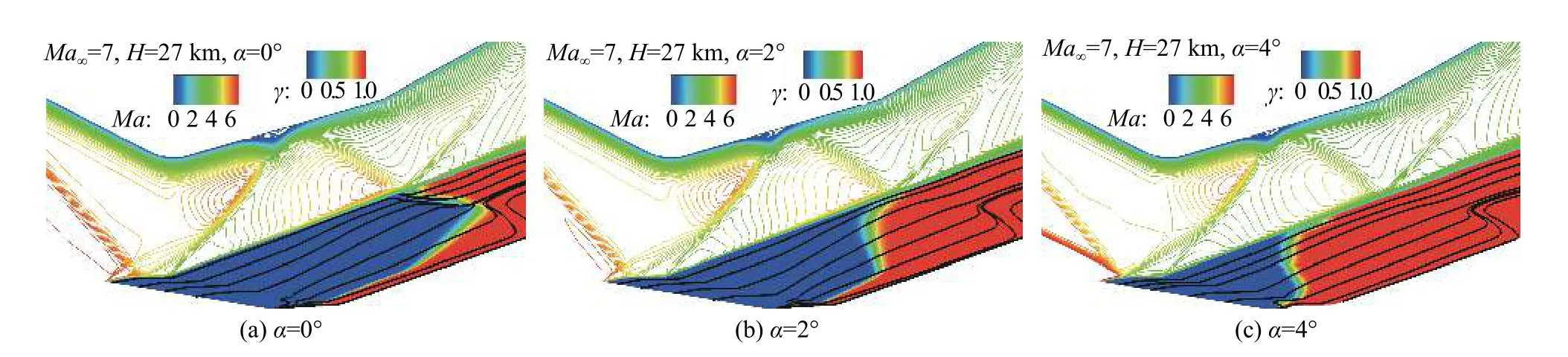
图5 不同攻角条件下类X-51A飞行器进气道对称面等马赫线分布以及进气道下壁面间歇因子和表面极限流线分布（Ma∞ = 7，Re∞ = 4.21×106/m）Fig. 5 Mach number distributions in the symmetrical plane, limit streamlines and intermittent factor distributions on the lower wall of the X-51A-like vehicle inlet at different angles of attack (Ma∞ = 7, Re∞ = 4.21×106/m)

图6 不同雷诺数条件下类X-51A飞行器迎风面壁面间歇因子和表面极限流线分布（α = 0°）Fig. 6 Intermittent factor distributions and limit streamlines on the windward side of the X-51A-like vehicle at different Reynolds numbers (α = 0°)

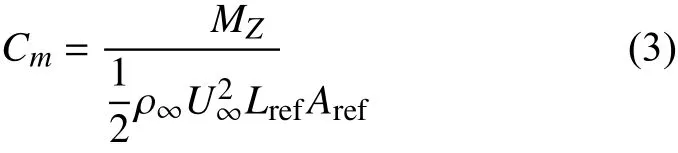
其中，L、D和MZ分别为飞行器的升力、阻力和俯仰力矩（抬头为正）。ρ∞为来流密度，U∞为来流与飞行器之间的相对速度。参考面积Aref选取类X-51A飞行器底部投影面积，Aref= 0.368 m2，参考长度Lref选取类X-51A飞行器机身全长，Lref= 4.27 m。飞行器质心位置为x= 2.134 m，y= -0.098 5 m，z= 0 m，坐标原点为飞行器头部顶点。升力L垂直于来流方向，阻力D平行于来流方向，因此，在攻角α≠ 0°情况下，升力系数CL和阻力系数CD由轴向力系数CA和法向力系数CN按照以下公式转换获取：

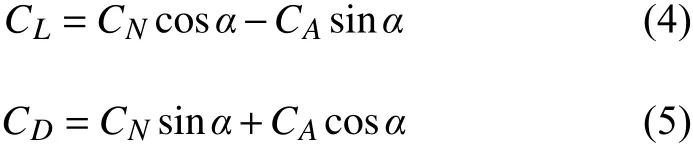
类X-51A飞行器所受的气动力和力矩主要来自机身、前体压缩面、进气道内壁面、尾喷管以及尾翼的贡献，这些部件产生的气动力和力矩相互作用、彼此影响，形成了类X-51A飞行器整体气动力和力矩特性。

图7给出了采用全层流、改进的k-ω-γ转捩模式和SST湍流模式三种方法计算得到的类X-51A飞行器全机升力系数CL随攻角和马赫数的变化趋势。根据薄翼型假设推导出的超声速、小攻角条件下翼型升力系数与攻角、马赫数之间的关系可知，随着攻角增大，翼型升力系数几乎线性增加；随着马赫数增大，翼型升力系数逐渐减小，且升力线斜率亦减小。从图7给出的计算结果可知，随着攻角增大，层流、转捩和湍流计算得到的类X-51A飞行器升力系数线性增加，与薄翼型假设理论推导趋势一致。随着马赫数增大，类X-51A飞行器升力系数逐渐减小，升力线斜率亦减小，同样与薄翼型假设理论推导趋势一致。说明本文对类X-51A飞行器全机升力系数预测结果合理。

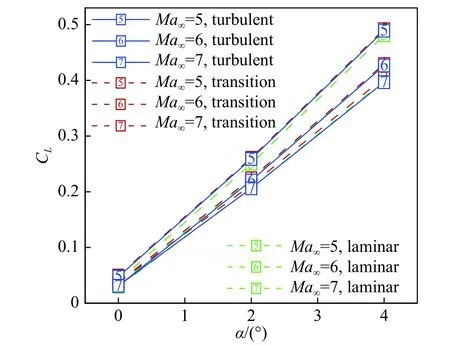
图7 层流、转捩和湍流计算得到的类X-51A飞行器升力系数对比Fig. 7 Comparison of lift coefficients of the X-51A-like vehicle calculated from laminar, transition and turbulent flows

此外，从图7可观察到，层流、转捩和湍流三种方法计算得到的类X-51A飞行器全机升力系数差异很小。考虑到飞行器升力由上下壁面压差产生，层流、转捩和湍流计算得到的类X-51A飞行器壁面压力整体差异不大，仅在分离区因分离区大小的区别导致局部压力有所差异，进而导致飞行器全机升力系数有较小差异，而边界层转捩因合理控制了飞行器前体压缩面、进气道、机身侧缘等部位的分离区，最终得到的升力系数略高于层流和湍流的计算结果。

图8给出了采用层流、转捩和湍流方法计算得到的类X-51A飞行器阻力系数随攻角和马赫数的变化趋势。为详细分析边界层转捩对飞行器阻力系数的影响规律，将飞行器总阻力CD系数分为两部分：由空气黏性引起的摩擦阻力系数CDf和与压力相关压差阻力系数CDp。

首先，从整体上看，本文计算工况中，层流、转捩和湍流三种方法计算得到的类X-51A飞行器阻力系数随攻角和马赫数的变化趋势基本一致。随着攻角增大，飞行器上下壁面压差增大，压差阻力系数增长显著，摩擦阻力系数变化较小，最终导致总阻力系数增加。随着马赫数增大，压差阻力系数减小，而由于对应的飞行高度增加，自由来流雷诺数降低，空气黏性作用增强，因此摩擦阻力系数增大。对于总阻力系数而言，由于摩擦阻力系数在总阻力系数中所占比例略小（CDf,lam/CD,lam=11.84%～25%，CDf,tms/CD,tms=30.57%～41.43%，CDf,turb/CD,turb=33.2%～48.75%），因此总阻力系数变化趋势与压差阻力系数一致，随着马赫数增大而减小。

其次，对于层流、转捩和湍流三种计算方法而言，由于转捩和湍流计算抑制了边界层分离，因此转捩和湍流计算得到的压差阻力系数较层流结果略减小。而对于摩擦阻力系数，由于湍流边界层产生的壁面摩擦阻力远大于层流，因此转捩和湍流计算得到的类X-51A飞行器摩擦阻力系数较层流结果显著增大，如图8（c）所示。摩擦阻力系数的显著增加最终导致飞行器总阻力系数增加，本文计算工况中，转捩和湍流计算得到的类X-51A飞行器总阻力相比于层流计算结果分别增加了ΔCDf,tms-lam= 21.19%～27.41%和ΔCDf,tur-lam= 27.52%～38.72%。湍流相比于转捩预测得到的阻力系数偏高ΔCDf,tms-tub= 4.1%～14.64%。可见，边界层的流动状态对飞行器阻力系数影响巨大，若不考虑边界层转捩会使得阻力系数预测存在20%～30%的误差，极大影响整个飞行器的气动性能设计。

由升力系数和阻力系数易得到类X-51A飞行器的升阻比L/D，如图9所示。随着攻角增大，飞行器升阻比增大；随着马赫数增大，飞行器升阻比减小。转捩计算得到的升阻比整体小于层流计算结果。湍流计算得到的升阻比最小。

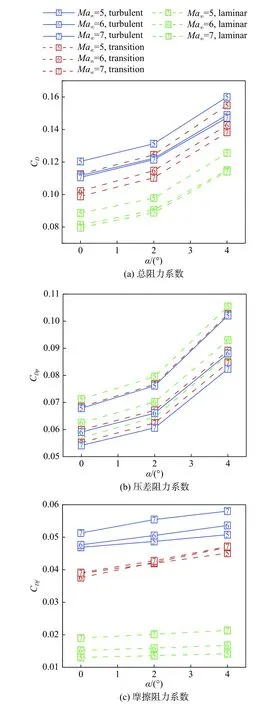
图8 层流、转捩和湍流计算得到的类X-51A飞行器阻力系数对比Fig. 8 Comparison of drag coefficients of the X-51A-like vehicle calculated from laminar, transition and turbulence

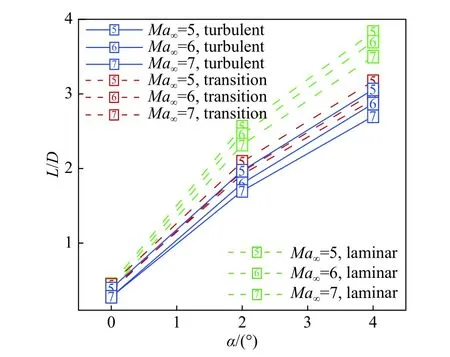
图9 层流、转捩和湍流计算得到的类X-51A飞行器升阻比对比Fig. 9 Comparison of lift-to-drag ratios of the X-51A-like vehicle calculated from laminar, transition and turbulent flows

力矩的平衡直接关系到飞行器的稳定性和操纵性。图10给出了采用层流、转捩和湍流方法计算得到的类X-51A飞行器俯仰力矩系数随攻角和马赫数的变化趋势。从图10可以看到，层流、转捩和湍流计算得到俯仰力矩系数随攻角和马赫数的变化规律基本一致。随着攻角增加，俯仰力矩系数线性减小，飞行器产生低头力矩，促使恢复之前的平衡状态，表明飞行器在不进行俯仰舵面控制时具有纵向静稳定性。随着马赫数增加，俯仰力矩系数略增大，但不如随攻角变化显著。

图10 层流、转捩和湍流计算得到的类X-51A飞行器俯仰力矩系数对比Fig. 10 Comparison of pitching moment coefficients of the X-51A-like vehicle calculated from laminar,transition and turbulent flows

5 边界层转捩对进气道性能的影响

进气道作为高超声速飞行器推进系统的主要气流压缩部件，其性能直接影响飞行器的整个推进系统，而边界层流动状态又直接影响进气道内流场特征以及性能参数，因此，研究边界层转捩对高超声速飞行器进气道的影响具有重要的工程应用价值。本节对比层流、转捩和湍流的计算结果，分析边界层转捩对类X-51A飞行器进气道性能的影响，主要通过飞行器喉道截面流量系数φ和喉道截面增压比π来评估飞行器的进气道性能特性。

图11给出了类X-51A飞行器进气道示意图。其中，飞行器喉道截面距离进气道唇口795.51 mm，高度为83.55 mm，喉道截面面积为Ath= 0.024 m2。飞行器前体压缩面和进气道入口截面沿x轴方向投影面积为A0= 0.102 m2。

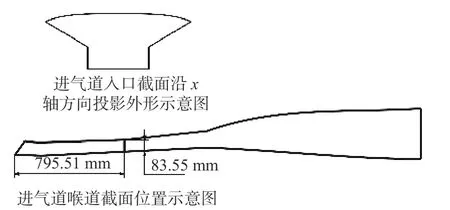
图11 类X-51A飞行器进气道示意图Fig. 11 Schematic of the inlet of the X-51A-like vehicle

进气道喉道截面的参数通过以下方法给出。

5.1 喉道截面流量系数ϕ

这里定义的喉道截面流量系数为进气道喉道截面捕获的流量与进气道前方未经扰动的自由来流流量之比，可表示为：

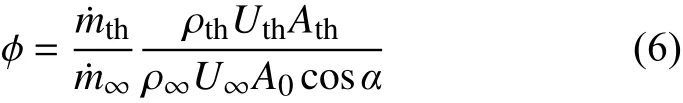
5.2 喉道截面增压比π

增压比是衡量进气道气流压缩程度的参数，这里将其定义为喉道截面面积平均静压pth与进气道前方自由来流静压p∞之比：

对于高超声速飞行器而言，基准流场产生较大的增压比同时有较高的总压恢复系数是发动机性能优良的基本要求。

图12给出了采用层流、转捩和湍流方法计算得到的类X-51A飞行器喉道截面参数随攻角和马赫数的变化趋势。图12整体上看，层流、转捩和湍流三种方法计算得到的类X-51A飞行器喉道截面流量系数φ和喉道截面增压比π随攻角和马赫数的变化趋势基本一致。随着马赫数增加，头部激波更贴近物面，激波从进气道唇口外打到唇口内，唇口溢流减弱，且进气道外压段气流转折角增加，进入进气道的来流流量增加，最终使得喉道截面流量系数增加，如图12（a）所示，又因进气道内气流压缩程度增强，因此喉道截面增压比增高，如图12（b）所示。

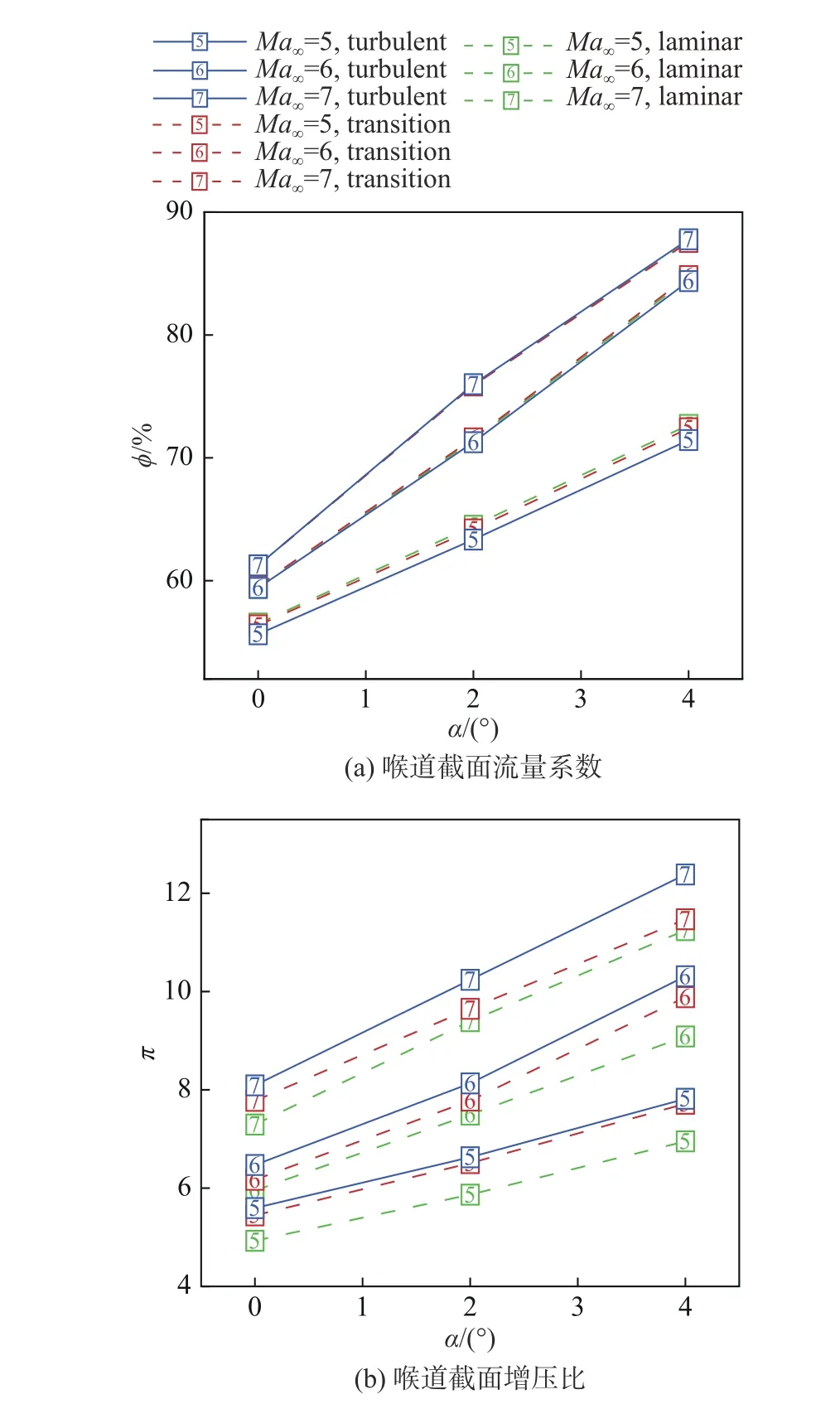
图12 层流、转捩和湍流计算得到的类X-51A飞行器进气道性能参数对比Fig. 12 Comparison of inlet performance parameters of the X-51A-like vehicle calculated from laminar,transition and turbulence

由于边界层的层/湍流状态直接影响进气道内的流场特征，因此层流、转捩和湍流三种方法计算得到的类X-51A飞行器喉道截面流量系数φ和增压比π均有所差异。从图13给出的层流、转捩和湍流三种方法计算得到的类X-51A飞行器进气道流向不同截面马赫数分布可以看到，由于边界层从前体压缩面便开始发展，因此进气道上壁面边界层较下壁面更厚。三种方法中，层流计算得到的边界层最薄，抗分离能力也最弱，在前体压缩面拐角处（图14（a））、进气道上壁面以及进气道上下壁和侧壁相交的角区均出现了边界层分离，分离涡结构显著，尤其是到尾喷管部分，分离涡结构发展更为明显。湍流计算得到的边界层整体较层流结果偏厚，且抗分离能力增强，前体压缩面拐角处未分离（图14（c）），且进气道内分离涡结构不如层流边界层显著。转捩计算得到的边界层在压缩面拐角处之前与层流结果一致，压缩面拐角之后，转捩发生，边界层开始增厚，进气道内的边界层厚度介于层流和湍流两者计算结果之间，但抗分离能力与湍流边界层类似（图14（b））。由于边界层的层/湍流状态对类X-51A飞行器前体部位波系结构影响微弱，仅边界层厚度有所差别，因此三种方法计算得到的进气道喉道截面流量系数差异不大，如图12（a）所示，转捩和湍流计算得到的喉道截面流量系数与层流计算结果之间的差异分别在0.46%和1.74%以下。

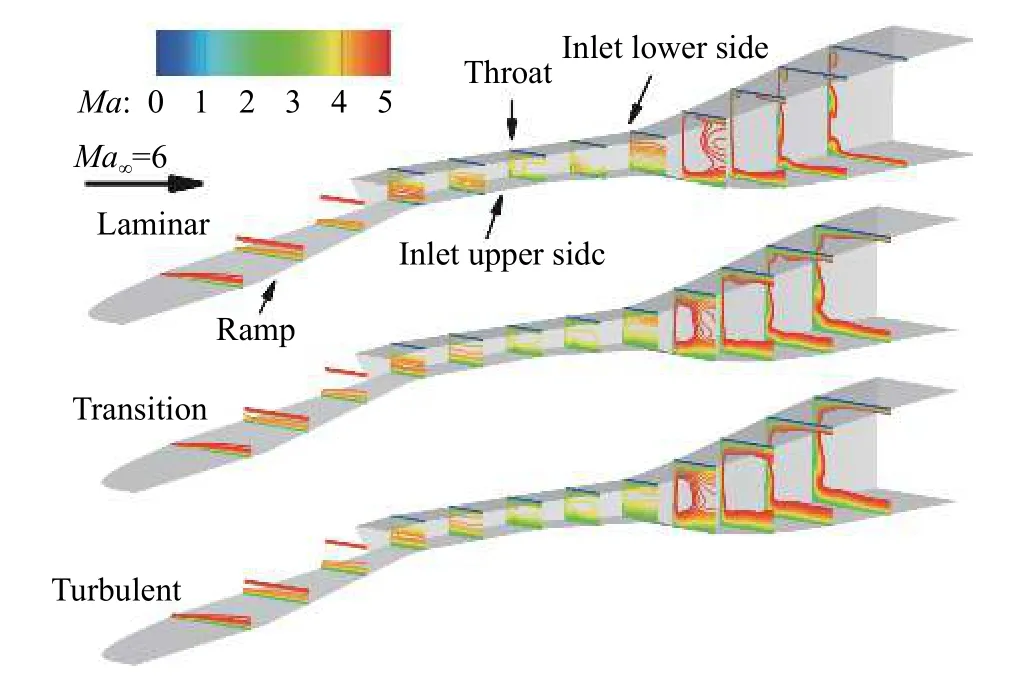
图13 层流、转捩和湍流计算得到的类X-51A飞行器进气道流向不同截面马赫数分布（Ma∞ = 6，H = 23 km，α = 4°）Fig. 13 Mach number distributions at different cross sections of the inlet of the X-51A-like vehicle calculated from laminar,transition and turbulent (Ma∞ = 6, H = 23 km, α = 4°)

虽然边界层流动状态对喉道截面流量系数影响较小，但对增压比影响较大。由于转捩和湍流计算得到的进气道边界层增厚，且进气道上壁面分离区减小，反射激波向前移动，使得第三道反射激波经过喉道截面（图14（d）～（f）），使得喉道截面低马赫数范围增大（图14（g）～（i）），导致计算得到的流量平均马赫数减小，而与之对应的喉道截面增压比增大（图14（b））。转捩和湍流计算得到的喉道截面增压比较层流计算结果的增大量分别为Δπtrns-lam= 1.97%～10.99%和Δπturb-lam= 8.47%～13.52%。

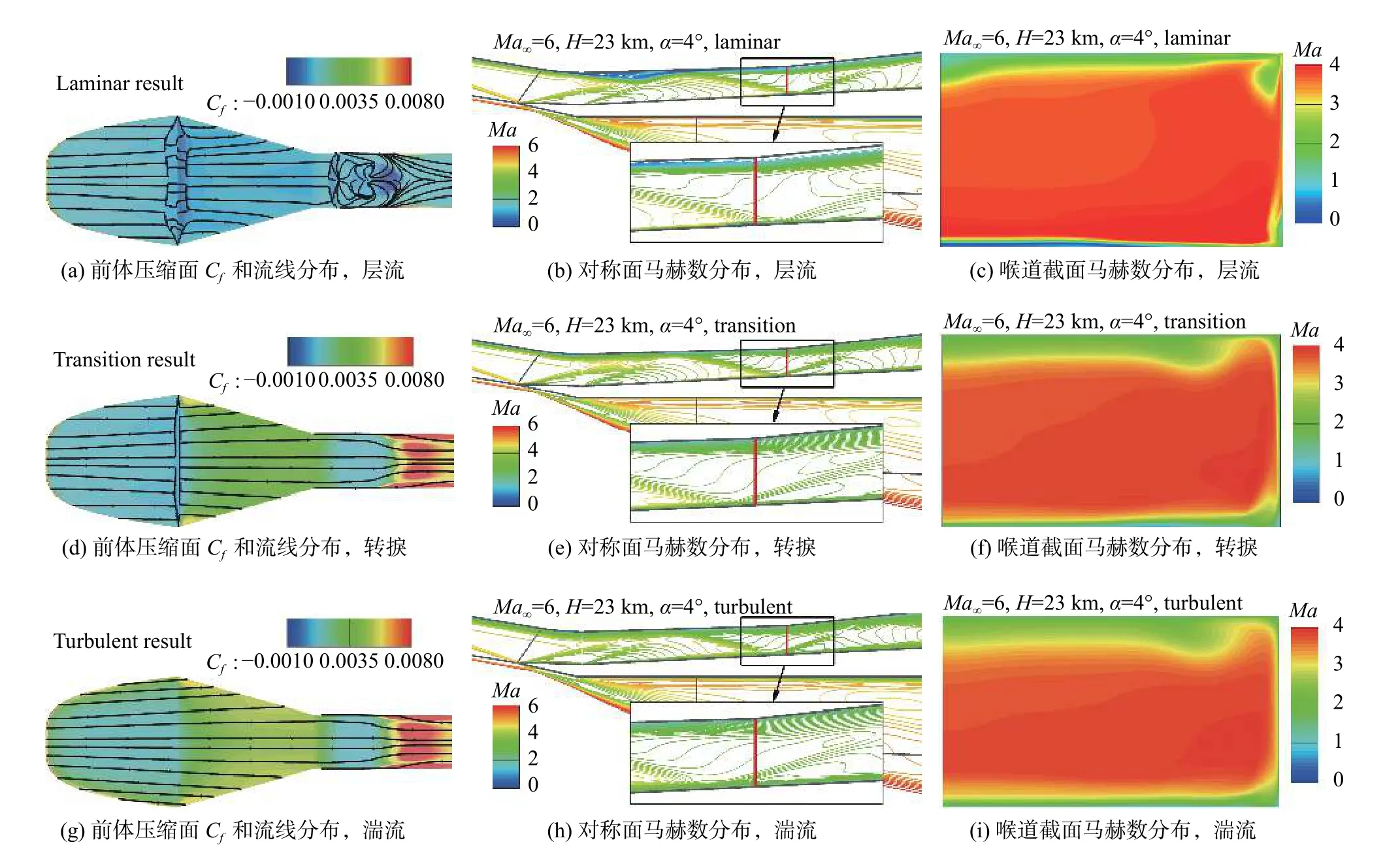
图14 层流、转捩和湍流计算得到的类X-51A飞行器进气道对称面和喉道截面马赫数分布（Ma∞ = 6，H = 23 km，α = 4°）Fig. 14 Mach number distributions in the inlet symmetrical plane and the throat section of the X-51A-like vehicle calculated from laminar, transition and turbulent flows (Ma∞ = 6, H = 23 km, α = 4°)

6 结 论

本文以类X-51A飞行器全机为研究对象，将改进的k-ω-γ转捩模式应用于高超声速复杂外形飞行器的边界层转捩预测，并系统分析了边界层转捩对类X-51A飞行器气动力和进气道性能的影响规律，研究得到的主要结论如下：

1）随着攻角增大，类X-51A飞行器背风面转捩起始位置向上游移动显著；侧面、前体压缩面以及迎风面，转捩起始位置随攻角变化较小；进气道内的转捩起始位置与激波/边界层干扰位置的变化趋势一致。随着马赫数增大，来流雷诺数降低，飞行器背风面转捩起始位置逐渐延迟，且攻角越小，延迟效应越显著；侧面和迎风面，转捩起始位置随着雷诺数减小小幅延迟；前体压缩面，在雷诺数减小到4.21×106/m时，转捩起始位置从压缩面拐角处延迟到进气道唇口附近。

2）边界层转捩对飞行器升力系数、阻力系数、升阻比以及俯仰力矩系数均有一定影响，如果不考虑边界层转捩，采用全层流计算飞行器气动力特性，则会低估升力系数和阻力系数，高估升阻比，尤其是阻力系数，本文计算工况下，低估差量可达20%～30%，升力系数和俯仰力矩系数预测误差虽然较阻力系数偏小，但在一定飞行姿态下，也可以达到5%和8%。因此，准确预测边界层转捩对正确估计飞行器气动力特性具有重要意义。

3）边界层转捩对类X-51A飞行器进气道喉道截面流量系数影响较小，但对喉道截面增压比影响较大。与全层流计算结果相比，边界层转捩会降低喉道截面马赫数、提高增压比；但相比于全湍流的计算结果，边界层转捩会增大喉道截面马赫数、降低增压比。考虑到层流边界层易分离、严重时将导致发动机不启动，湍流边界层又会影响进气道性能，因此，对于高超声速飞行器，控制边界层在前体压缩面的转捩位置，对提高超燃冲压发动机效率、保证其成功运行具有重要意义。