爆破振动峰值速度预测的SVM模型及应用

彭府华，刘 建

（长沙矿山研究院有限责任公司，湖南 长沙 410012）

工程爆破过程中的爆破振动往往会带来一些难以避免的负面效益。因此，在爆破前对爆破振动进行准确的预测是如何降低爆破振动影响的关键技术问题［1，2］。影响爆破振动的因素较多，且各影响因素之间是一种非线性、不确定的复杂关系，因此对爆破振动进行预测是一个困难的问题。传统的萨道夫斯基公式仅考虑段药量、爆源距两参数，忽略了高程差和岩体结构构造等其它因素的影响，处理过于简单，存在不科学性及预测误差较大等缺点［3］。国内外许多学者也采用了萨道夫斯基公式以外的一些方法进行爆破振动预测研究，比如采用神经网络方法等进行爆破振动预测［4］，这类方法和传统萨道夫斯基公式相比一定程度上提高了爆破振动预测精度。但是采用神经网络算法计算爆破振动速度过程中，必须提供大量的训练样本才可以取得较高的计算精度。

近年来普遍采用的一种统计学习算法是SVM方法，该方法的原理是将低维空间映射到高维空间，从而将低维空间下不能线性分割问题转化为高维空间下最优超平面问题［5，6］。SVM 是一种针对小样本、小概率事件的机器学习模型，它的优势在于可以利用有限的样本信息，在模型复杂性和学习能力中间找到最优解。将SVM回归理论应用于某矿山爆破振动峰值速度预测，进而探讨该模型的可行性及适用性［7～10］。

1 SVM回归理论

SVM方法的本质是将低维空间映射到高维空间，从而将低维空间下不能线性分割问题转化为高维空间下最优超平面问题。

SVM估计函数为：

式中：W，b代表超平面方程 f（x）＝W·x＋b的系数。在ε不敏感损失函数的意义下，上述估计函数可转化为如下优化问题：

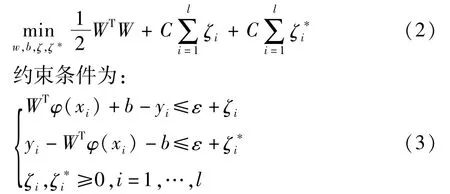
采用对偶理论可将公式（3）转化为如下二次规划问题：

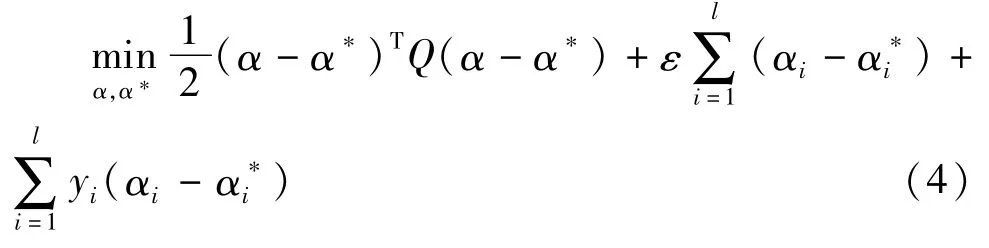
约束条件为：

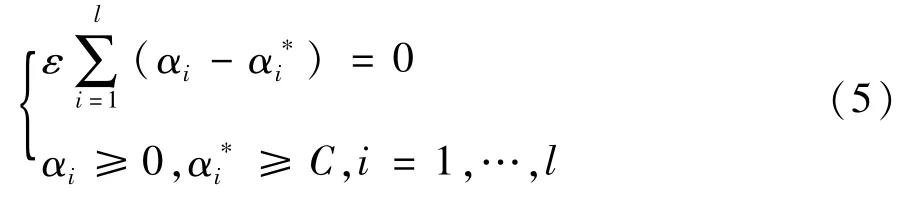
通过二次规划算法可得SVM回归预测模型为：

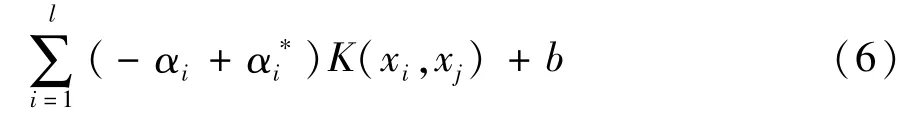
式中：αi为引入的拉格朗日乘子；K（xi，xj）代表支持向量机由低维空间向高维空间转换所采用的核函数类型；b是偏置量。

2 工程实例

以34组某大型露天矿山台阶爆破实测振动数据为例进行建模，数据取自文献［2］，建模过程中，将前面27组数据作为训练样本，剩余7组数据（星号标记）作为预测样本，见表1。

表1 某露天矿山台阶爆破实测振动数据

数据收集过程中，仅对爆破振动峰值速度影响最大的三个主要因素进行了量测，分别为最大段药量Q/kg、爆心距R/m和高程差H/m。采用互信息方法对最大段药量、爆心距和高程差三个影响因子的影响程度进行计算，互信息值（MI）越大，表明影响程度越高，影响因子互信息值如图1所示，由图1可知，爆心距对爆破振动峰值速度影响最显著，其次是高程差，最后是最大段药量。

图1 影响因子互信息值

萨道夫斯基经验公式是目前爆破振动峰值速度预测应用最广泛的方法：

式中：v为爆破振动速度/cm·s-1；Q为最大段装药量/kg；R为爆心距/m；K和α为与地形、地质条件相关的系数。

萨道夫斯基提出的经验公式中仅有两个未知参数，由此可知至少需要两组实测数据才能确定上述未知参数。采用萨道夫斯基经验公式对表1数据进行回归计算分析，可确定具体公式为：

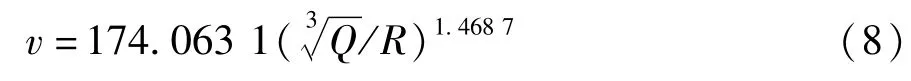
回归分析的相关系数达到0.958 6，可见数据拟合程度较好。

由于各个影响因素及峰值速度的数量级不同且同时带有单位，因此先对原数据归一化处理，使所有影响因子值和峰值速度值属于［0，1］［10］；然后利用sigmoid核函数将前27组数据进行SVM模型训练，同时利用网格算法和3折交叉验证方法确定最佳初始参数C和g，其中C为惩罚参数，g为核函数参数。最终，最佳初始参数为C＝4，g＝1，如图2所示。图3为预测结果，预测数据与原始训练数据大致相当，这清楚地表明SVM模型的有效性。

图2 SVM参数选择结果

图3 训练样本预测结果

模型训练完毕之后，对28～34号样本进行预测，预测结果见表2，表中同时给出了BP神经网络与经验公式的预测结果。由表2可知，SVM回归预测结果优于BP神经网络和萨道夫斯基经验公式。利用萨道夫斯基经验公式进行爆破振动峰值速度预测，其最大相对误差为52.36%，最小相对误差为4.31%。而采用SVM模型，其最大相对误差为18.50%，最小相对误差仅为2.28%。由此可知，萨道夫斯基经验公式在某些时候具有极大的不准确性。这是由于其仅考虑最大段药量和爆心距两种影响因素，忽略了其它因素的影响。此外，在采用BP神经网络进行峰值速度预测过程中，每执行一次都会得到不同的结果，表2中BP网络预测结果只是多次预测中的一次。这说明BP神经网络具有很大的局限性，其结果稳定性较差，这主要是由于神经网络算法过度依赖于阈值和初始权值，每次进行网络初始化时，都会对阀值和初始权值随机赋值，然后通过训练样本学习过程获得最佳网络阀值与权值，但由于参数过多，其每次学习优化结果都不同。而SVM模型则不同，其仅具有两个参数，多次执行其获得的结果大致相同，这表明SVM具有较好的稳定性。

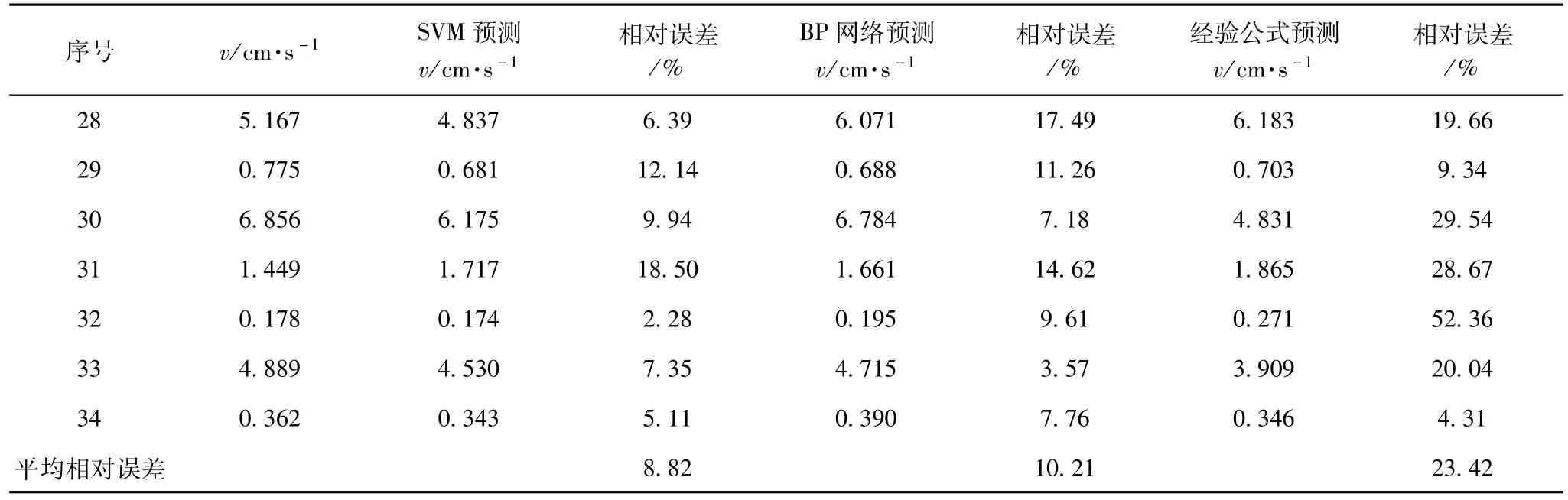
表2 预测结果与实测值对比

3 结 论

基于SVM的爆破振动峰值速度预测模型，以某矿山爆破实测振动数据为例对该模型进行检验，同时将SVM模型预测结果与BP神经网络模型和萨道夫斯基经验公式预测结果进行对比，结果表明该模型是可行的，其预测结果不仅优于BP神经网络和萨道夫斯基经验公式，而且还具有良好的稳定性。由于萨道夫斯基经验公式只考虑最大段装药量和爆心距两个影响因数，忽略了其它因素的影响，导致利用该公式时在某些时候具有极大的不准确性，因此，在实际工程中应配合其它预测方法共同计算爆破振动峰值速度。同时对爆破振动影响因素对峰值速度影响的相关性进行了计算，结果表明对爆破振动峰值速度影响最显著的因数为爆心距，其次是高程差，最后是最大段药量。