变频空调器电子元器件板肋式散热器仿真与优化

空调设备及系统运行节能国家重点实验室 珠海格力电器股份有限公司 陈 红 广东省制冷设备节能环保技术企业重点实验室 珠海格力电器股份有限公司 赵树男

0 引言

变频空调室外机电子元器件一般封装在电器盒内，避免因接触水、灰尘等造成主板短路烧毁或者漏电安全隐患。高温天气机组运行时，功率器件发热量大，封闭的保护结构造成散热困难，器件表面易快速达到限温保护，导致机组频繁降频或死机，严重影响用户正常使用。长期高温的工作环境也会给电子元器件的可靠性及寿命带来不利影响。研究数据表明，器件温度每升高1 ℃，可靠性下降5%[1]。设计合理的散热方案是提高空调产品品质的关键。散热技术的研究热点包括风冷冷却、液体冷却[2]、半导体制冷、热管技术[3]、液氮冷却等。受成本、安装空间及可靠性等因素制约，传统的风冷冷却仍为工程应用首选方案。

由于风扇噪声和可靠性等问题对风冷散热方案的限制，强迫风冷散热效能较低，一般不超过1 W/cm2[4]。当散热环境恶劣、散热器结构设计不佳时，无法充分满足散热需求。研究人员从肋片参数、形状、风道结构等方面对散热器性能进行了大量研究。Arularasan等人仿真研究了风量25.5 m3/h、热功率100 W时，不同几何参数板肋式散热器的性能，分析了各参数对压降及热阻的影响，提出了仿真条件下最佳参数组合的肋片结构[5]。Rao等人研究了TLBO算法在板肋式散热器多目标设计中的适用性，提出了优化的散热器结构并进行了仿真分析，发现空气流通冷却系统板肋式散热器的动态散热性能优于冲击流系统[6]。Yuan等人对肋间加工有销钉的板肋式换热器进行了仿真研究，结果表明，销钉直径和风速对热工性能有显著影响，排列方式及距离等影响不显著[7]。Ismail等人对开孔肋片的湍流特性进行了研究，发现圆形开孔肋片比其他形状开孔肋片具有更好的流动特性及散热性能[8]。Mohan等人仿真分析了配合风扇强制风冷时，肋片各参数对散热性能的影响，基板厚度为2.5～5.0 mm、肋片厚度为0.5～1.5 mm范围内，随着基板、肋片厚度增大，散热性能得到强化[9]。李树云等人通过设计导流罩、引风孔等结构，改变了散热器所处流场环境以提高散热性能，元器件表面温度得以大幅降低[10-11]。刘伯春对散热器周围风场进行了仿真分析，通过优化散热器的安装位置获得更优的散热条件，如来流风速、温度等，提升其散热效果[1]。

板肋式散热器的性能不仅受来流方向、速度和温度的影响，还与热源分布和肋片结构有密切关系。本文通过数值仿真分析研究各因素对电子元器件板肋式散热器散热的影响，并分析已有板肋式散热器的不足，提出一种新型板肋式散热器，有效解决某型变频空调室外机高温天气元器件温度超标导致机组异常的问题。

1 研究对象

板肋式散热器装设于室外机风机腔内，肋片朝下，通过基板与置于上端的电子元器件紧密贴合对其进行散热，见图1、2。接触面的导热作用将电子元器件的产热传递至散热器基板及肋片，在风扇抽吸作用下，散热器表面与流经的空气发生强制对流换热，热量随空气排出风机腔实现持续散热。

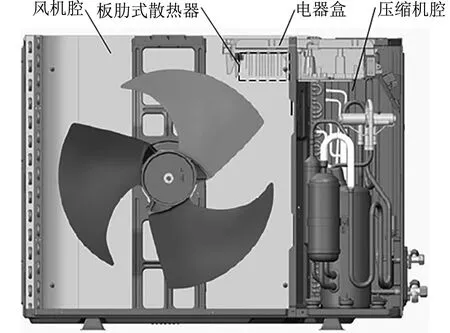
图1 室外机三维结构图

注：IGBT为绝缘双极晶体管；IPM为智能功率模块。图2 电子元器件分布示意

以板肋式散热器为研究对象，计算分析其结构对电子元器件散热性能的影响。重点考察散热片温度均匀性及电子元器件表面温度，电子元器件表面温度最高不得超过90 ℃。物理建模时，同时设置散热器固体域及外场空气域，以考虑散热片周围空气流动状态对散热性能强化作用的影响。为避免模型太过复杂，导致仿真资源无法满足或计算收敛性差，对实机模型进行简化，选取板肋式散热器周围区域(300 mm×300 mm×360 mm)建立几何计算模型。模型中不考虑室外机风扇及冷凝换热器，通过在入口面设置速度边界实现来流空气模拟计算。散热器基板尺寸为200 mm×100 mm×4 mm，肋片高度、厚度分别为60、1 mm，采用不等间距排列，间距取5～9 mm。具体几何模型见图3。

图3 散热器几何计算模型

2 数值模拟

2.1 网格划分

板肋式散热器性能仿真包括散热器基板及肋片固体导热仿真和其所处空气流场的流动传热仿真，需同时划分散热器固体网格和空气流体网格。使用ICEM软件对几何模型进行非结构化网格划分，如图4所示。网格参数的设置需综合考虑计算精度及成本[12]。

图4 网格划分

2.2 计算模型

本文所涉及的传热过程仅考虑导热和对流，忽略热辐射。

热对流包括强制对流和自然对流。一般地，当Gr/Re2≥0.01时(其中Gr为格拉晓夫数；Re为雷诺数)，自然对流的影响不能忽略[13]。

(1)

式中g为自由落体加速度；β为热膨胀系数；Δt为壁面温度与环境温度之差；l为特征长度；u为流体速度。

按式(1)计算得到空气的Gr/Re2值约为0.4，仿真模型需考虑浮升力作用。

β可近似表示为

(2)

式中ρ为流体密度；t为流体温度。

为便于计算自然对流，采用Boussinesq假设[14]，对动量方程中与体积力有关的密度项按式(3)进行计算，其他项密度均作常数处理。

ρ=ρ0[1-β(t-to)]

(3)

式中ρ0为流体的参考密度(常数)；to为操作(工作或环境)温度。

应用Fluent软件对散热器进行数值模拟分析，质量、能量、动量通用控制方程为[15]

(4)

式中τ为时间；ø为通用变量；U为速度矢量；Γø为广义扩散系数。

使用稳态压力基求解器，开启自由落体加速度项。湍流模型选用RealizableK-ε两方程模型，近壁面用壁面函数处理法。压力项、湍动能项采用二阶迎风离散格式，动量项、能量项采用QUICK离散格式，压力-速度耦合方程采用SIMPLE算法[16]。对模型内部流场、温度场进行仿真计算，监测电子元器件表面温度。质量、动量方程残差达到1×10-3，能量方程残差达到1×10-6，监测温度基本不变时，即认为计算达到收敛[12]。

2.3 物性处理与边界条件

空气密度参数设置为Boussinesq模型，其他物性参数均设置为常数。散热器壁面按铝材设定，密度、比热容、导热系数等均为常数。

在功率器件、散热片和风道等区域连接处设置接触。固-固交界面通过界面处的傅里叶热传导方程，实现热源与散热器间的传热模拟[17]。流-固交界面设置为耦合边界，软件耦合求解对流传热方程，并自行传递两域间计算参数。

设定功率器件为体热源，根据发热功率与体积的比值计算体热源密度。其中，整流桥发热功率取35 W，IPM模块为40 W，2个IGBT、二极管均为15 W。

几何模型各壁面边界设置如下：

1) 后侧壁面为速度入口边界，根据样机实测风速设置入口风速1.6 m/s，温度48 ℃；

2) 左、下侧壁面为压力出口边界；

3) 其他壁面均设置为绝热壁面。

3 散热器仿真分析

对原型散热器进行仿真计算，并使用CFD Post后处理软件进行流场、温度场分析。

3.1 流场

板肋式散热器及其周围空气的速度矢量如图5所示。从图5b可以看出：空气垂直于通道截面进入散热器流道后，速度矢量沿肋片长度方向重新分布；靠近基板壁面空气流速逐渐降低，沿气体行经路程低速区域逐步扩大。分析认为，空气流经基板固定壁面时，受摩擦力作用，贴近壁面的流速降低[13]。在基板的起始段，低速区域很小，沿着肋片长度方向，由于壁面黏滞力的影响逐渐向流体内部传递，低速区域逐渐增大。同时，散热器处于外部自由流场空间中，受阻力作用影响，大部分空气垂直进入肋片通道后，通过下部自由出口离开肋片通道。这两方面因素使得空气流动背离基板方向，运动轨迹呈现弯曲形态，肋片出口截面流量远小于肋片入口截面。

图5 散热器速度矢量图

原型散热器设计有不同间距肋片，见图5c。单个通道内，靠近两侧肋片壁面的空气流速低，中心位置流速高；间距大的通道平均流速高于间隙小的通道。单个通道两侧均有固定壁面，下部为自由出口，使得通道内空气流动类似于管道流形态，黏滞力作用区域局限在靠近两侧壁面的薄层内，中心区域黏滞力造成的切应力可忽略不计，导致中心区域流速远高于壁面处。同时，黏滞力作用以流动阻力为表现形式，通道越窄，流动阻力越大，通道内空气的平均流速就越小。

由以上分析可知，沿肋片长度方向，基板处空气低速区逐渐增大，肋片通道中空气流量减小，散热条件变差。随着肋片间距的减小，通道流动阻力变大也会减小空气流量，但肋片间距减小，意味着在散热器原基板尺寸上可以设计更多的肋片以增大散热面积，因此肋片间距、长度、数量等因素需要综合考虑。

3.2 散热器表面温度场

从图6所示的温度分布云图可以看出，散热器表面温度沿肋片长度方向呈现入口低、出口高的特点；沿肋片高度方向，受导热与对流耦合作用影响，温度呈弧线梯度降低趋势。各元器件表面温度，IPM模块最高，IGBT次之，二极管最低。

图6 散热器表面温度分布云图

根据流场分析可知，空气流经散热器时，靠近基板区域的空气流速较低，对流传热减弱，导热占主导地位。在肋片长度方向，受壁面黏滞力影响，低速区域逐步扩大，空气导热层厚度随之增大，换热效率越来越低；同时，入流空气通过与基板及肋片壁面接触吸收器件产热，受浮升力影响，热量沿着肋片长度方向发生累积，空气温度升高，传热动力逐渐减小，进一步恶化了肋片尾端散热环境。沿肋片高度方向，空气温度不同导致密度的差异。在密度差作用下，热空气上浮聚集在基板区域，使得基板壁面散热受阻，热量通过肋片根部沿高度方向进行传导。根据傅里叶导热定律，距离热源越远，肋片温度越低。且肋片远端空气温度较低，流速较高，对流作用较肋片根部强烈。因此，肋片高度方向表现出温度逐渐降低的趋势。

各元器件体热源密度大小及所处散热环境的优劣影响了其表面温度高值的差异分布。体热源密度大小排序为：整流桥>IGBT>IPM模块>二极管，而散热环境优劣排序为：整流桥>IGBT、二极管>IPM模块。两因素综合作用的结果导致IPM模块温度过高，成为限制机组正常工作的瓶颈。

对原型散热器进行实验测试，以考察仿真模拟计算的可靠性。测试数据及模拟值的对比见表1。

表1 测试值与模拟值的对比

结果显示，模拟与测试值偏差不超过10.8%。计算结果与测试值总体偏差不大，且沿空气流动方向元器件温度分布趋势一致，因此，认为仿真模型的数值结果是合理的，可用于优化方案仿真分析。仿真误差来源如下：计算模型忽略了流体特性随温度的变化；未考虑散热器与环境间辐射热传递；器件实际运行功率与模型设定发热功率存在一定差异。

4 优化方案

低风速散热环境下，单向长肋片板肋式散热器尾端的空气流量小，且温度较高，散热效果不佳，导致IPM模块表面温度超限。针对此问题，对原型散热器进行结构优化。由图5a可知，空气从进风面垂直进入后，部分沿肋片外侧绕流后转向出风。此部分空气不仅流速较高，且温度较低，十分利于散热。因此，在散热器尾端设计横向肋片，引入绕流空气解决尾端空气流量小且温度较高的问题。同时，针对肋片长度过长会导致基板附近低速热空气聚集，影响器件及时排热，优化的散热器将肋片沿长度方向进行分段，段间设计旁通间隙，使得紧贴基板的低速热空气可从间隙排出，改善基板散热环境。

优化的板肋式散热器，分3段进行肋片布置。第1、2段为竖向肋片，第3段为横向肋片。各段肋片间设计旁通间隙，第2、3段肋片通过“L”形肋片结构进行分隔。肋片厚度保持不变，间距取5 mm，使得原有基板尺寸不变条件下，肋片数量可增加2片。对于空气低速区，散热面积的增加对于能效改善效果较好。

肋片具体布置见图7a，几何模型见图7b。

图7 散热器优化结构

采用已验证的仿真模型对优化结构散热器进行仿真计算与分析。优化结构散热器速度矢量分布见图8，表面温度分布见图9。

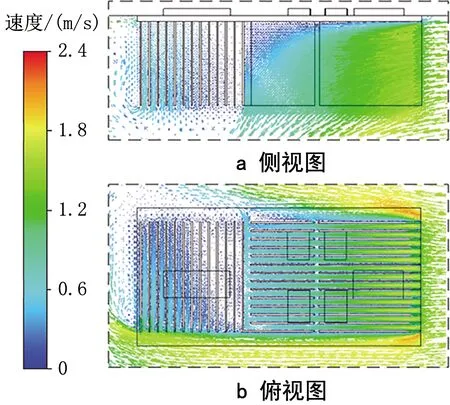
图8 优化结构散热器速度矢量图

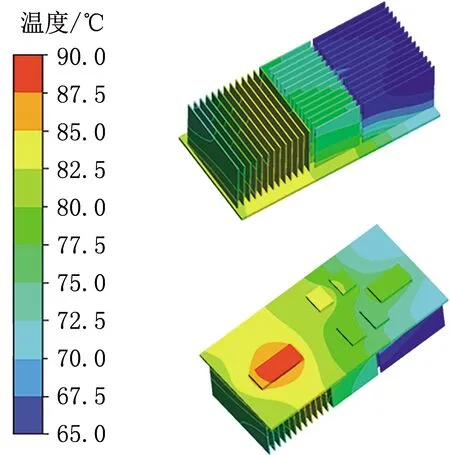
图9 优化结构散热器温度分布云图

由图8可以看出，沿肋片外侧绕流的部分空气，在阻力调节作用下发生转向进入横向肋片通道。受惯性作用力影响，横向肋片始端的肋片通道空气流量较小，随着行程路径增长，进入横向肋片进行对流换热的空气流量逐渐增大。横向肋片通道平均流速达到0.6 m/s左右，相较原型散热器有明显提升。在第2、3段肋片间设计的“L”形肋片有效分隔了竖向肋片通道与横向肋片通道，避免竖向肋片通道中吸收了整流桥、二极管、IGBT器件产热的空气进入横向肋片通道，不利于IPM模块散热。

肋片下部远离基板的空气流速远高于靠近基板的空气，相应地，其受惯性力作用的影响也较大。因此，肋片下部的稍高流速的空气更易从散热器底部排出；而紧贴基板的热空气因流速接近于0，更易受热空气膨胀力的作用从旁通间隙排出，汇入散热器外侧空气场。旁通间隙的设计有利于分段排热，减少热量的累积。

对比图6、9可知：元器件及肋片表面温度显著降低；横向肋片通道，始端肋片温度稍高，尾端肋片温度稍低，整体温度均低于原型散热器；两段竖向肋片通道，长度、高度方向温度梯度较原型散热器均有明显减小，且肋片间温差减小，均匀性得到改善。

根据流场分析可知，横向肋片始端通道流量稍小，随行程路径增长，流量逐渐增大，因此温度表现出逐渐降低的趋势。而且，由于隔断了散热器前端传递过来的热量，并通过错向设计引入了绕流低温空气，使得IPM模块所处区域肋片散热效果得到较大提升。

对于竖向肋片通道，基板处热空气从旁通间隙排出，使得空气导热层厚度减小，热阻降低。相较原型散热器，元器件产热能更快地从基板传递给空气进行散热，散热效率提升。

优化前后元器件表面平均温度如图10所示。相较原型散热器，优化方案各元器件温度降低约 2.8～4.6 ℃。定义温降值与优化前温度值的比值为优化率，则该优化方案的优化率为3.2%～5.5%，优化效果明显。其中，IPM模块由超限温度90.5 ℃下降至87.6 ℃，可充分保障机组正常使用。

受外侧高速空气流动惯性影响，靠近“L”形肋片的横向肋片区域流量较小，可通过调节横向肋片占比进一步优化散热器能力。

5 结论

1) 使用Fluent进行板肋式散热器仿真模拟，模拟与测试值偏差不超过10.8%，可为板肋式散热器优化设计提供依据，节省开发成本。

2) 低风速散热环境下，板肋式散热器散热效果受肋片长度、间距、数量等因素影响。沿肋片长度方向，肋片内的风量逐渐减小，温度逐渐升高，不利于散热。肋片间距越小，通道流动阻力越大，流量越小。肋片数量越多，可用散热面积越大，越有利于散热。在散热器一定尺寸条件下，需综合考虑各因素的耦合效果。

3) 对处于较低风速散热环境的板肋式散热器，可采用多段肋片、错向肋片的设计来改善散热效果。多段肋片的段间间隙，可及时排出贴附基板的吸热空气，减小传热热阻；错向肋片流道，使得散热器的入口面积增大，参与有效散热的空气流量增大，且入口空气温度较低，传热动力大，也有利于快速散热。本文原型散热器经优化后，各元器件温度降低2.8～4.6 ℃，优化率约为3.2%～5.5%。