基于分位数回归P2P平台收益率风险度量的研究

陈瑞英，赵月旭

(杭州电子科技大学经济学院，浙江 杭州 310018)

0 引 言

近年来，在互联网金融发展的背景下，点对点网络借贷(Peer-to-Peer，P2P)随之崛起并进入发展的快车道，已在我国金融领域占有一席之地，对传统金融借贷的完善和发展起到积极作用，并对我国传统金融领域的改革起到推动作用。P2P网络借贷具有交易门槛低、收益率高、快捷性和便利性等特点，另外，借贷平台可以将投资风险给予最大程度的分散，有利于增强人们的风险防控意识。基于此，P2P网络借贷越来越受到人们的关注和青睐，为人们提供一种新的理财和募集资金途径，在一定意义上有利于我国普惠金融的发展。但是，P2P网络借贷也带来一些棘手问题，例如平台跑路和提现困难等。这些问题的出现使得投资人数从2017年开始出现递减趋势，借款人数反超投资人数。这一现象表明投资风险的加剧使投资者望而却步，但市场需求却在不断增大，对整个借贷市场造成冲击，给金融市场带来一定的风险。因此，P2P网络借贷风险度量的研究有着重要的实际意义。孙同阳等[1]以信用等级作为输出变量来建立决策树模型，较好地预测了P2P借贷风险；刘畅[2]用Logistic模型对P2P平台的信用风险进行研究，研究表明借款者违约的概率与其学历的高低、收入水平等因素成反比，而与贷款期限等其他4个指标成正比；卢金荣[3]从平台的数量和问题平台数量等变化角度出发，通过建立压力指数模型来构建风险度量指标；孙龙龙[4]通过因子分析法进行风险度量；周秋池[5]建立了以中证指数收益率为研究对象的指数广义自回归条件异方差(Exponential Generalized Autoregressive Conditional Heteroskedasticity，EGARCH)阈顶值模型，对互联网金融进行风险度量；黄芳等[6]采用同等权重的11个二级指标作为输入变量，建立了概率神经网络模型；邹明芮[7]建立了Lasso-logistic模型，一定程度上提高了预测准确率；傅毅等[8]假定资金流为泊松分布，建立均值-方差模型；王立勇等[9]建立二层次灰色关联模型构建评价体系，再计算风险值(Value at Risk，VaR)；陈守东等[10]对含有超越时间与相关收益率强度的极值风险进行度量分析。以往的一些研究通常将残差分布设为正态分布，或者采用单一的广义自回归条件异方差模型(Generalized Autoregressive Conditional Heteroskedasticity，GARCH)，这会导致与实际情况不符，模拟效果不理想。本文以我国P2P网络借贷平台的收益率为研究对象，对平均日收益率数据进行统计分析。考虑到金融时间序列数据具有尖峰厚尾、非对称和条件异方差性等特征，利用t分布的厚尾特性，在对GARCH族模型进行比较分析的基础上，建立了t-EGARCH模型，再结合分位数回归的方法，给出P2P平台收益率风险的估计值及实证分析。

1 基本理论

1.1 分位数回归模型

定义1[11]假设F(x)=P(X≤x)为随机变量X的分布函数，对任意的0<τ<1，定义

F-1(τ)=inf{x∶F(x)≥τ}

(1)

称F-1(τ)为随机变量X的τ分位数。

定义2定义损失函数为

(2)

式中，0<τ<1，μ为变量，函数I(·)为示性函数。

定义3设Z为一随机变量，{Z1,Z2,…,Zn}为其样本值，对任意的0<τ<1，Z的第τ样本的分位数的估计值为：

(3)

式中，δ为参数，γτ(·)为损失函数。

分位数回归根据数据处于不同的分位点来估计分布的信息，从而对数据进行全面描述。

1.2 t-EGARCH(1,1)模型

考虑到序列的非对称效应并结合数据的特点，Nelson[12]提出了EGARCH模型，其中误差项服从t分布，得到t-EGARCH(1,1)模型如下：

(4)

式中，at为随机误差项，c1和σt分别为平均收益率rt的均值和标准差，a0,c2,α1,β1和γ1为参数，εt为随机变量，且服从自由度为n的t分布。

本文给出如下的风险值估计量模型：

(5)

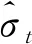
2 P2P平台收益率风险值的实证分析

2.1 数据的预处理

本文选取我国P2P网络借贷平台2016年4月1日至2019年3月17日的平均综合日收益率数据进行分析。选取区间内的数据虽不完整，但缺失数据量较少，采用拉格朗日插值方法对数据进行补全，最终确定的样本数据量为1 081个。

首先，使用Eviews软件对数据进行正态性检验，根据Q-Q图初步可以判断收益率有偏斜趋势，初步判断不服从正态分布。另外分布偏度为-0.016，分布呈左偏。峰度为3.123，大于3，分布呈现尖峰厚尾的特征。综上所述，我国P2P网络借贷平台的平均综合收益率分布呈左偏、尖峰厚尾和非正态分布等特征。然后，使用Eviews软件进行条件异方差检验。从我国P2P网络借贷平台的平均综合收益率的时序图可以看出，2016年至2019年期间的日收益率围绕在均值上下波动，部分时间表现出来的波动明显，因此对我国P2P网络借贷平台的平均综合收益率序列做单位根(Augmented Dickey-Fuller，ADF)检验，检验结果为平稳。最后，对该序列进行自相关检验，得到自相关系数超出了两倍的估计标准差，偏相关从14阶之后就落在两倍标准差内，并且Q统计量的相伴概率均小于0.05，故该序列在5%的显著性水平下，存在序列的自相关现象，自相关系数和偏自相关系数都显著不为0，因此存在自回归条件异方差(Autoregressive Conditional Heteroskedasticity，ARCH)效应。综上，我国P2P网络借贷平台的平均综合收益率序列存在尖峰厚尾、非正态分布、自相关性、条件异方差性和非对称性。

2.2 模型的选择

根据上述分析可知，为了更好地刻画P2P网络借贷平台的平均综合收益率序列的非对称性和条件异方差性，选取GARCH族模型。首先根据收益率序列分布类型做GARCH族模型假设，然后利用t检验并结合赤池信息准则(Akaike Information Criterion，AIC)、施瓦茨信息准则(Schwarz Criterion，SC)选择模型，各模型检验结果如表1所示。

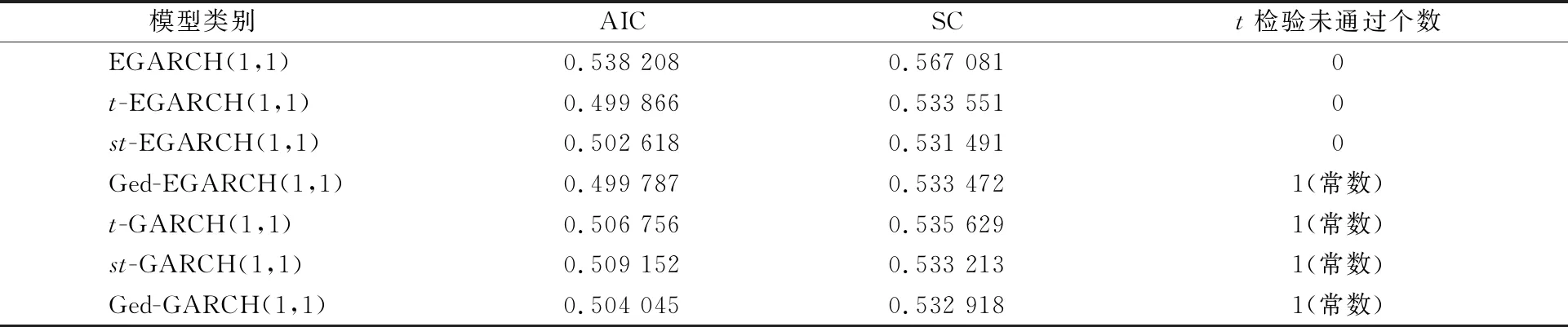
表1 不同模型的AIC,SC,t检验结果比较

由表1可知，我国P2P网络借贷平台的平均综合收益率适用于建立残差服从t分布的EGARCH(1,1)模型，通过Eviews软件计算得到t-EGARCH(1,1)模型的各参数及显著性检验，结果如表2所示。

表2 t-EGARCH(1,1)模型中各参数估计值以及显著性检验

由表2可知，模型的参数均通过了显著性检验，具体模型为：

(6)

当置信水平为(1-a)时，基于t-EGARCH(1,1)模型的VaR值计算公式为：

VaR(1-a)=ut+t(1-a),nσt

(7)

式中，ut为收益率的均值，t(1-a),n为自由度为n时，置信水平为(1-a)的t统计量值，σt为平均收益率的标准差。

2.3 基于分位数的t-EGARCH(1,1)模型及VaR值

基于分位数的t-EGARCH(1,1)模型的参数利用分位数回归的方法，通过最小化残差绝对值加权和来求解，估计量如下：

(8)

式中，yi为风险样本值，Xi,β为参数向量，γτ(·)为损失函数。

建立风险值模型为：

(9)

式中，τ为分位点。当τ取99%时，分别采用t-EGARCH(1,1)模型和基于分位数回归的t-EGARCH(1,1)模型预测2016年4月至2019年3月的VaR，结果如图1所示。

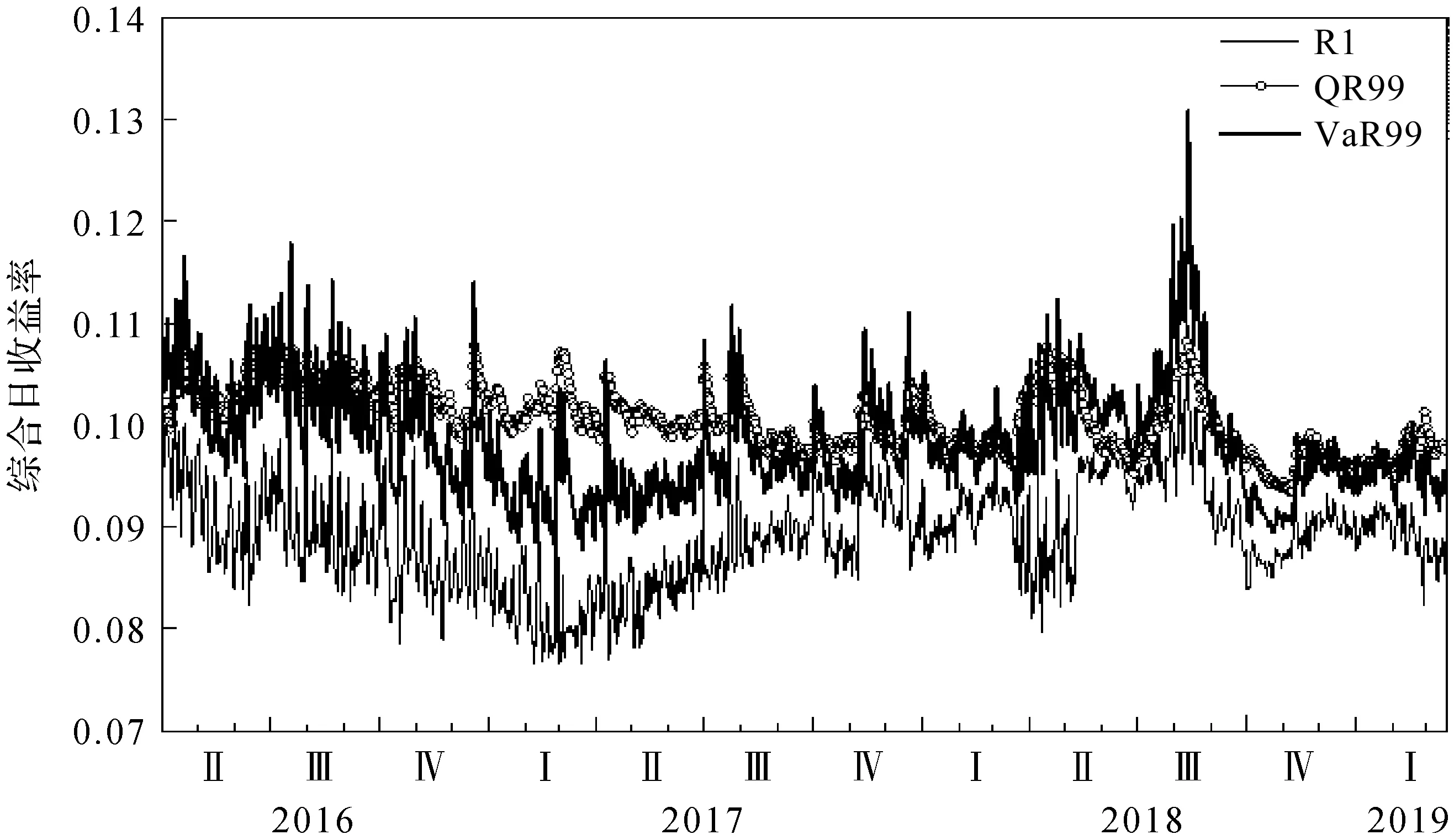
图1 日收益率、t-EGARCH(1,1)和分位数t-EGARCH(1,1)的VaR预测值

图1中，横坐标为预测的年份和季度，R1为综合日收益率，VaR99为t-EGARCH(1,1)模型的VaR预测值，QR99为基于分位数的t-EGARCH(1,1)模型的VaR预测值。从图1可以看出，在相同的显著性水平下，t-EGARCH(1,1)模型的VaR预测值变化幅度较大，说明模型高估了风险；基于分位数的t-EGARCH(1,1)模型的VaR预测值变化幅度适中，说明预测风险效果更好。

2.4 失败率检验

失败率检验法[13]检验的是VaR的预测结果对实际损失的覆盖程度。先由风险值模型算出预测的损失值，然后将其与实际的损失值进行比较，如果实际损失值大则为失败，否则为成功。假设失败的概率为p=α，统计失败的天数记为d0，d0除以观测的总天数d1得到失败频率d。建立原假设d=p(VaR值有效)，构造似然比检验统计量：

L=-2ln[(1-p)d1-d0×pd0]+2ln[(1-d)d1-d0×dd0]

(10)

表3 不同模型的失败率检验结果

由表3可以看出，基于分位数回归的t-EGARCH(1,1)模型的拟合成功率明显高于t-EGARCH(1,1)模型。因此，加入分位数回归后的t-EGARCH(1,1)模型对我国P2P网络借贷平台的平均收益率的风险度量效果更好。注意到P2P网络借贷是新兴金融产业，因此在发展过程中容易受到各种因素的影响，收益率波动越大对预测结果就会产生越明显的影响。

2.5 实验模拟检验

为了验证分位数t-EGARCH(1,1)模型的有效性和实用性，进行实验模拟检验。首先，生成样本量为1 026的非正态的随机序列，由分布特征分析，得到该序列的均值为0.56，偏度为1.629 5，大于0，为右偏，峰度为7.611 2，大于3，显示尖峰，J-B值为1 363.029，J-B的p值为0。然后，对数据进行ARCH检验，得到检验的p值小于显著性水平5%，说明序列存在条件异方差性。在95%的置信水平下，VaR的预测结果如图2所示。

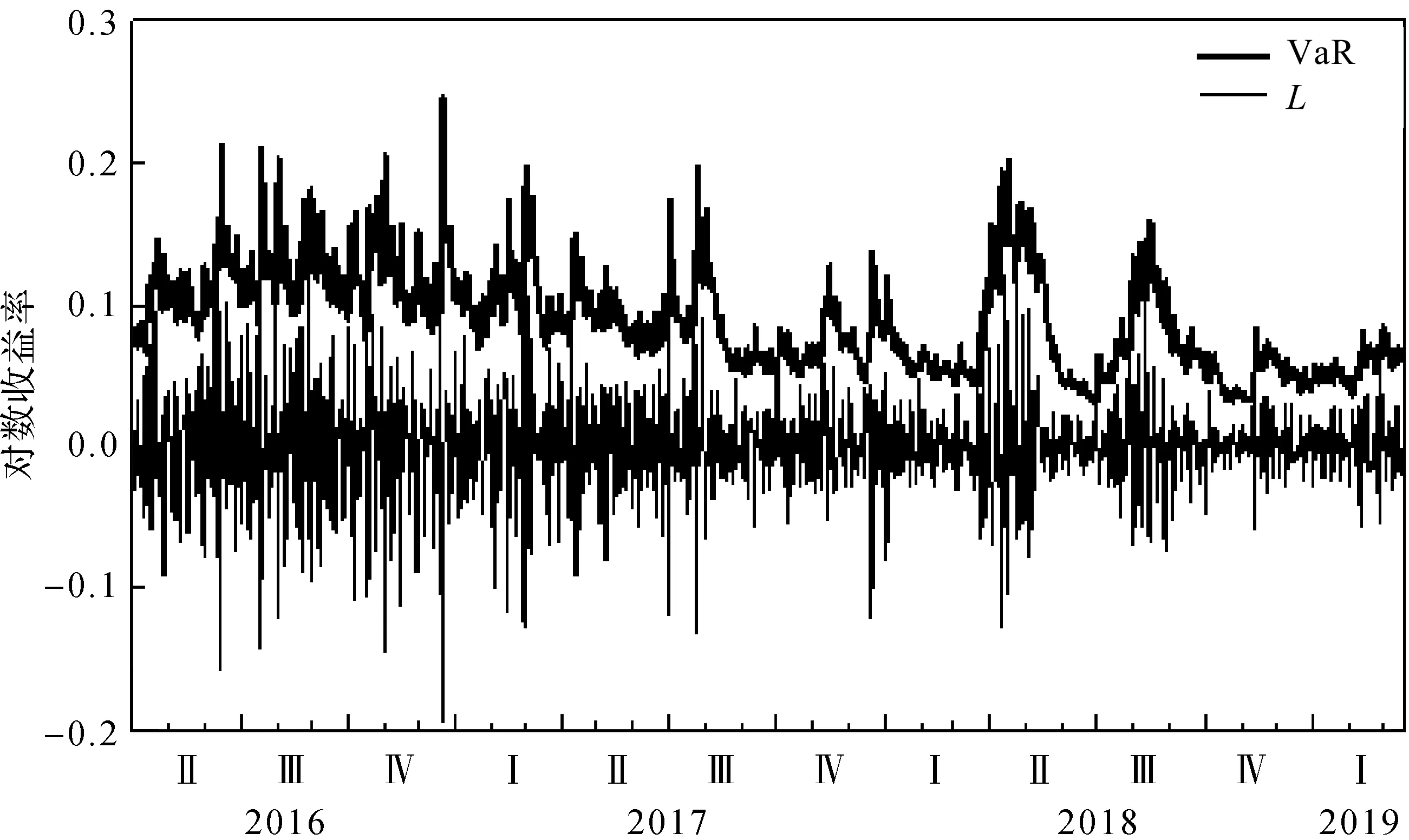
图2 对数综合日收益率和VaR预测结果

由图2可以看出，基于分位数回归的t-EGARCH模型的VaR度量效果较好。

3 结束语

本文研究了我国P2P网络借贷平台日平均收益率的风险值，建立了t-EGARCH模型，并利用线性规划给出风险的分位数估计。建立的分位数回归t-EGARCH模型在风险值度量方面较为稳健，且模拟效果较好。但是，本文风险值模型中的参数估计基于历史数据，当一些重大突发事件发生时，模型风险估计值与实际值有较大的差异，因此投资者在使用模型时要结合具体情况。