基于放电室均布模型的射频离子推力器研究
2021-06-23颜能文郭宁吴辰宸谷增杰杨兆伦
颜能文,郭宁,吴辰宸,谷增杰,杨兆伦
兰州空间技术物理研究所,兰州 730000
空间电推进技术是先进的宇航动力技术之一,可用于皮纳卫星、微纳卫星、小卫星的位置保持和姿态控制任务,大中型GEO卫星平台的轨道提升及小行星探测等任务。离子电推进是发展最早、应用最广、技术最成熟的电推进技术,可分为电子轰击型、电子回旋共振型和射频型。其中,射频型离子推力器是基于感性耦合放电的电推力器,具有比冲高、易于缩比和结构简单等优点[1],典型产品有德国RIT-10、美国BRFIT-3等,其中德国RIT-10已成功应用于ARTEMIS通信卫星的南北位置保持任务。射频离子推力器放电不依赖空心阴极,避免了空心阴极寿命对推力器任务的影响。相比于其他类型的离子推力器,射频型离子推力器对电参数调节响应更灵敏,特别适用于无拖曳控制、空间摄动力补偿等领域。掌握工作参数和结构参数对射频离子推力器放电性能的影响规律,实现快速响应调节、推力准确调节,是目前国际对离子推力器的研究热点之一[2]。
目前,数值仿真和试验研究是国际开展射频推力器研究的主要方式。数值仿真主要基于感性耦合放电模型开展,感性耦合放电模型可分为电磁模型[3]、变压器模型[4]、二维流体数值模型[5]和PIC/MCC动力学模型等[6],但上述模型计算周期长,成本高。本文采用依据电磁模型衍生发展的均布模型来描述射频离子推力器放电室内的等离子体特征,该模型具有计算速度快、成本低的特点[7]。法国国家科学研究院的Chabert等利用均布模型,研究了射频功率和工质流率对射频离子推力器性能的影响[8]。研究发现,增大工质流率和射频功率,推力器效率增加,工质利用率下降,但该计算过程未考虑栅极束流的引出模型,计算精度受限。本文在Chabert等人研究的基础上,研究了放电室长径比和栅极电压与推力器性能的变化规律;同时针对Chabert等未考虑栅极束流引出模型的缺陷,增加了对放电室栅极鞘层模型的模拟研究,并通过试验数据验证了模型可行性。
本文以兰州空间技术物理研究所研制的LRIT-40射频离子推力器为载体,研究了推力器的工作参数和结构参数对推力器性能的影响规律。结构参数为放电室尺寸(长径比:放电室长度L与半径R的比值);工作参数包括工质流率、栅极电压和射频功率等[9-10]。用于表征推力器性能的指标有推力、工质利用率和推力器效率[11]。
1 推力器数值模型及求解
1.1 LRIT-40结构及放电原理
LRIT-40射频离子推力器放电原理及结构如图1所示。

图1 射频离子推力器结构示意
推力器由放电室、射频天线、加速栅、屏栅、工质分配器和空心阴极等组成。放电室为长35 mm,半径20 mm,缠有5圈铜质射频天线的柱形陶瓷圆筒。射频功率通过射频天线耦合放电产生等离子体。由屏栅和加速栅组成的栅极组件用于引出和加速离子。空心阴极发射与离子束同等电量的电子来中和离子束流[12-13]。
1.2 放电室模型
均布模型以能量平衡方程和粒子数平衡方程为控制方程,以射频功率、工质流率和栅极电压为输入参数,在确定的工况下联立求解控制方程得到等离子体密度ne、电子温度Te、中性气体分子密度n0以及束电流Ib等,进一步计算出输出参数工质利用率、推力器效率和推力。为了简化计算,均布模型作以下假设:
1)放电室内的等离子体密度分布均匀。
2)放电室内各处电子、离子和中性气体分子温度各自服从均值分布。
3)中性气体分子温度与放电室器壁温度相等。
4)离子温度与中性气体分子温度相等。
均布模型仅考虑氙气工质的激发、电离和弹性碰撞动力学过程,对激发碰撞电离和退激等粒子碰撞动力学过程不予考虑。
(1)中性气体分子密度
当推力器的工况和工质流率确定后,放电室内放电达到动态平衡时,中性气体分子密度将不再随时间变化。假设推力器能够产生Ib的束电流,则溢出放电室的中性气体流率为:
式中:Qin为通入放电室的工质流率;e为元电荷电荷量。式(1)也可表达为:
式中:ηc=0.5为克劳辛系数;Ta=0.17为屏栅的光学透明度;Ag为栅极面积;vg为中性气体分子速度[14]。
由式(1)(2)得到中性气体分子密度表达式为:
式中:ηmd为工质利用率。
(2)粒子数平衡
均布模型假设等离子体呈电中性,即离子密度等于电子密度ne=ni。中性气体分子密度通过式(3)求得,等离子体密度平衡方程为:
式中:Kiz为氙气的电离系数,Kiz=(Kiz1+Kiz2)/2;vbohm为玻姆速度;V为放电室体积;Aeff为电子扩散到壁面的有效损失面积[15]。
式(4)等号左边第一项为单位时间内电离产生的电子数,主要与等离子体密度、中性气体分子密度和电离系数Kiz有关;第二项表示单位时间内扩散到壁面损失的电子数,放电达到动态平衡后,式(4)成立。
Kiz1=10-20×[-(3.97+0.64TeV-
6.38e-12.127/TeV]ve
式中:TeV为电子温度,单位eV;ve为电子速度。
式(4)中Aeff的表达式为:
Aeff=2hRπRL+2hLπR2L
式中:hR和hL分别为鞘层径向边缘和轴向边缘的等离子体密度与放电室中心位置等离子体密度的比值[16],
式中:neR和neL分别为鞘层径向边缘和轴向边缘的等离子体密度;λi为离子-中性气体分子碰撞自由程,与中性气体分子密度、电荷交换与弹性散射碰撞的截面均值有关,λi=1/(n0Si),Si=10-18m2。
(3)电子能量平衡
电子能量平衡方程能够体现射频功率对放电室内等离子体状态参数变化的影响,表达式如下:
式中:Pabs为电子吸收功率密度;Ploss为电子损失功率密度;Rind为等离子体等效电阻;Irf为射频线圈中通入的电流。
输入推力器的射频功率部分被射频天线吸收,余下部分通过感性耦合原理被电子吸收,放电室内电子在感生电场中获得的能量大小与射频电流呈正相关[17]。
式中:Rcoil为射频天线电阻。联立式(5)(6)可得吸收功率密度为:
由式(7)知,电子吸收功率密度与输入感性网络的射频功率成正比,与等离子体等效电阻成正相关。等离子体等效电阻为:
式中:N=5为射频天线匝数;w=2 MHz为射频频率;ε0为真空中的介电常数;J0、J1分别为零阶、一阶的第一类贝塞尔函数;k1为等离子体中的复波数,
式中:k0为自由空间中的波数;εp为等离子体的复介电常数,
式中:wpe为电子等离子体频率;vw为弹性碰撞频率[18-19]。
电子的能量损失机制与电子温度、推力器尺寸和中性气体分子温度有关,
Ploss=Eiznen0Kiz+Eexcnen0Kexc+
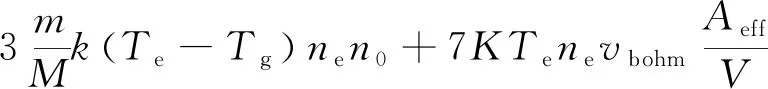
式中:Tg为中性气体分子温度;m为电子质量;M为氙气原子质量;Eiz为氙原子的第一电离能;Eexc=11.6 eV为激发能;Kexc为激发截面,
式(8)等号右端第1项是中性气体分子电离所耗费的能量,第2项为激发消耗能量,第三项为中性气体分子与电子发生弹性碰撞后的能量传递,第4项为损失到壁面的电子所携带的能量。
1.3 栅极鞘层模型
放电室内等离子体中的离子经过栅极组件引出加速,产生推力。栅极鞘层是在放电室屏栅区域形成,能够影响推力器引出的束流大小。通过拟合栅极鞘层模型,提高了仿真模型计算精度。单个屏栅孔产生的束电流表达式为:
式中:N0为栅极孔数;A为单个屏栅孔的有效面积,即屏栅孔鞘层边界面的面积。 从式(9)可知,A是影响束电流的重要因素。
经典鞘层模型的计算过程复杂,计算周期长,本文为了简化鞘层计算,对鞘层模型进行近似模拟。图2是鞘层模拟示意。
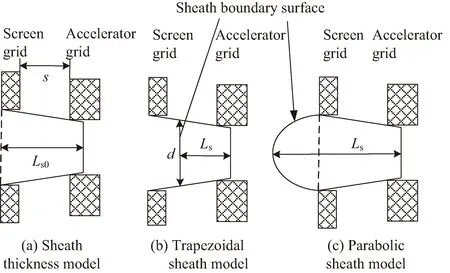
图2 栅极模型
鞘层厚度是指鞘层边界面中心点到加速栅的距离,如图2中LS所示。由图2可知,鞘层边界面的面积与鞘层厚度有关,鞘层厚度越大,则鞘层边界面积越大。鞘层厚度用直流鞘层模型进行计算[19]:
式中:US为栅极电压;λd为德拜长度,
当鞘层厚度大于图2(a)中的LS0时,鞘层深入到放电室内;当鞘层厚度小于LS0时,鞘层在两栅之间,LS0由推力器栅极组件确定:
式中:LAcc为加速栅厚度;LScr为屏栅厚度;s为栅间距。
当LS
1.4 模型求解
模型求解是联立LRIT-40推力器设计参数、工质的电离反应参数及工作参数求解参数方程(3) ~(5),以获得确定工况下放电室内的等离子体参数和推力器性能参数。
中性气体分子密度n0的求解是模型求解的第一步。首先确定工质流率并假定工质利用率初始值ηmd来计算n0,将计算得到的n0带入式(4)(5)中,利用数值解析方法求解ne、Te和Ib,进而计算出工质利用率ηmde。再将ηmde作为初始迭代计算,直到解出的ηmde与ηmd在误差允许范围内,即完成一组数据的求解。
非线性方程组的求解必须保证计算精度和数值解收敛。利用迭代法求方程组数值解要求迭代初值尽量接近方程组的解以确保迭代收敛并减少迭代次数。
2 LRIT-40推力器性能试验
TS-6S是兰州空间技术物理研究所用于电推力器试验的真空试验系统。试验系统构成如图3所示。
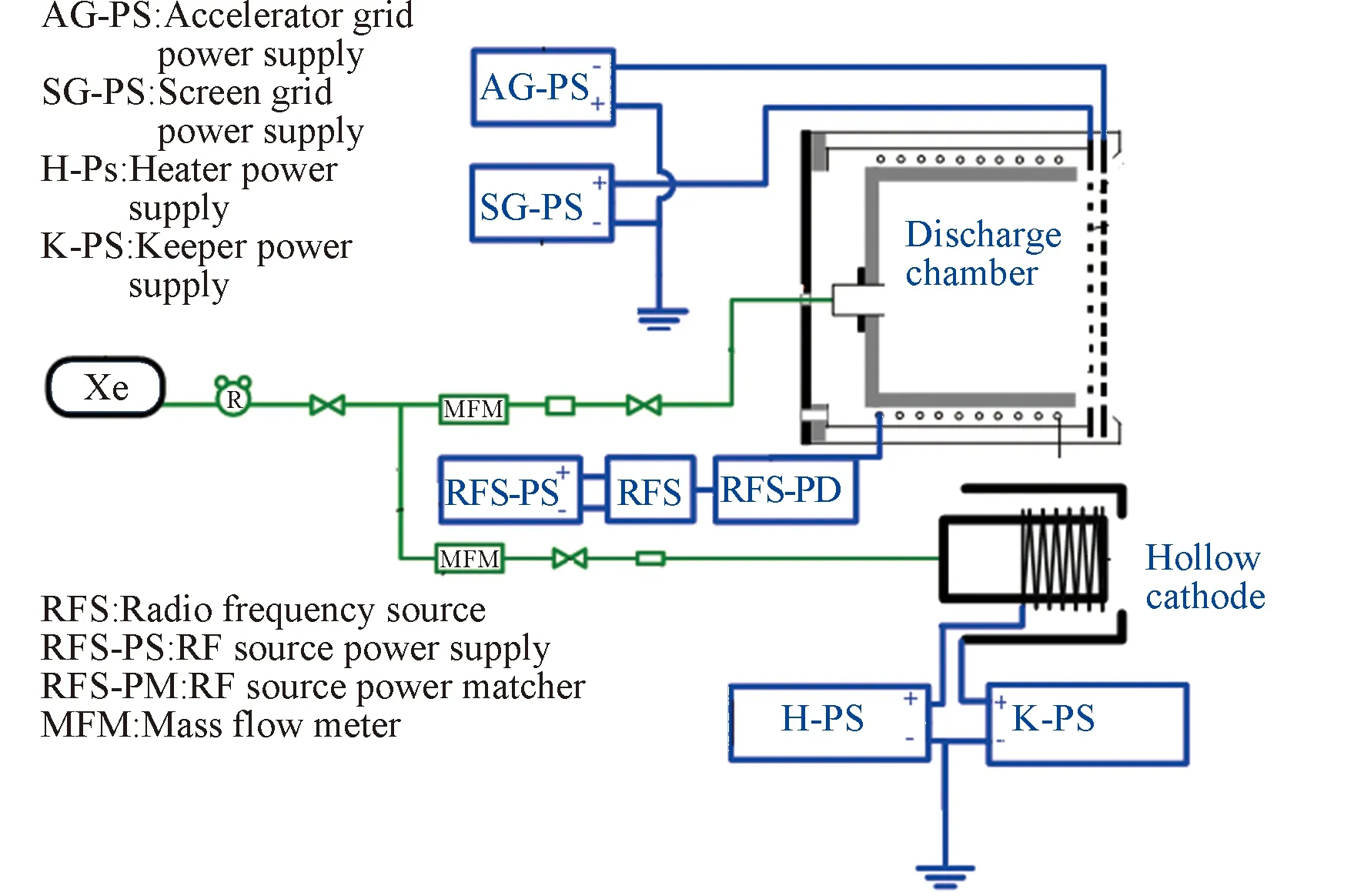
图3 LRIT-40 射频推力器试验结构示意
LRIT-40推力器性能试验需要4部直流电源和1台射频源。4台电源包括:屏栅电源输出电压为0~2 000 V,电流0~1 A;加速电源输出电压为0~1 000 V,电流0~1.5 A;触持级电源输出电压为0~100 V,电流0~19 A;加热电源输出电压为0~35 V,电流0~7.5 A。射频源为固定频率2 MHz的500 W射频源。图4为LRIT-40推力器稳定放电时的羽流。

图4 LRIT-40推力器放电羽流
进行推力器试验时,加速电压为200 V,加速电压用于阻止电子返流。
3 结果与讨论
3.1 结果分析
(1)栅极电压对LRIT-40性能的影响规律
图5是射频功率65 W、工质流率为0.121 6 mg/s工况下,LRIT-40推力器性能参数随栅极电压的变化规律,其中MOD为模型仿真结果,EXP为试验结果。

图5 推力器性能-栅极电压关系
图5横轴为栅极电压,最大值为1 650 V,纵轴为推力器性能参数。试验结果与仿真结果趋势相符,性能参数值均随着栅极电压的增大而增大。
当栅极电压为1 500 V时,曲线斜率增大。曲线斜率增大的原因有两点:其一是由于栅极电压增加,鞘层深入到放电室内,电压对鞘层边界面积的影响增大,推力器性能参数随栅极电压的变化更加显著;其二是随栅极电压增大,用于加速离子的功率占总功率的比值增大,提高了推力器效率。
因此,推力器工作时,栅极电压应大于1 500 V,以提高推力器效率。从而在相同速度增量的任务中降低推进剂需求量,减轻电推进系统重量,来增加卫星有效载荷。
(2)射频功率对LRIT-40性能的影响规律
图6是栅极电压为1 000 V、工质流率为0.121 6 mg/s工况下,LRIT-40推力器性能参数随射频功率的变化规律。

图6 推力器性能-射频功率关系
从图6可知,推力器的性能参数随射频功率的增加呈上升趋势,且试验结果与仿真计算结果相符。射频功率增加,等离子体吸收的功率增大,电子温度增高,工质的电离度增大,射频离子推力器的性能得以提升,但增加趋势随射频功率的增大而减缓。由此可见,设计推力器时,适当提高射频功率有利于提高推力器性能。
(3)工质流率对LRIT-40性能的影响规律
图7是射频功率100 W、栅极电压为1 000 V工况下,LRIT-40推力器性能参数随工质流率的变化规律。
由图7可知,推力器的推力随工质流率的增大一直增大;工质利用率随工质流率的增加,先增大后减小,当工质流率为0.1 mg/s时达到最大。推力器效率随工质流率的增大不断增大,当工质流率大于0.125 mg/s时,推力器效率趋于平缓,几乎不再增加。
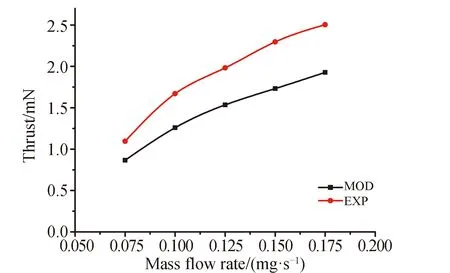
图7 推力器性能-工质流率关系
工质利用率随工质流率先增大后减小的原因是:当工质流率小于0.1 mg/s时,随流率增加,放电室内中性气体分子密度增加,电子与中性气体分子碰撞几率增加,工质利用率增加;当工质流率大于0.1 mg/s,电离过程受射频功率限制,继续增加流率,单位时间内产生离子数几乎不变,因此工质利用率反而下降。
为保证推力器效率,推力器工作时,工质流率应保持在0.1 mg/s左右。
(4)长径比对LRIT-40性能的影响规律
图8是射频功率为65 W、栅极电压为1 000 V、工质流率为0.121 6 mg/s工况下,根据放电室均布数值模型计算得到的LRIT-40推力器性能参数随长径比的变化规律。
从图8可知,随着长径比增大,相同工况下推力器性能参数均呈下降趋势。这是由于当增大放电室长径比时,单位时间内损失到壁面的离子数增加,导致壁面功率损失增加,降低推力器效率。

图8 推力器性能-放电室长径比关系
3.2 误差分析
从第3.1小节结果分析可以看出,仿真结果与试验结果存在误差。通过分析模型的建立和求解过程,造成误差的原因有以下几点:
1)模型简化。均布模型只是等离子体在放电室内的空间平均,忽略等离子体真实分布对推力器放电性能的影响,因此均布模型不能完全反映真实的分布模型而致使误差,模型简化造成的误差是主要误差。
2)气体放电模型简化。虽然氙气的电离反应相比于双原子分子更为简单,但也有17种之多,而均布模型仅考虑了氙原子的主要动力学过程,包括激发、电离和弹性碰撞以及氙离子的壁面复合。其余反应虽然对整体放电模型影响较小,但也会造成误差。
3)鞘层模型误差。本文使用了抛物面模型和梯形模型组合的简化鞘层模型,该鞘层模型与实际鞘层模型存在差异,为计算结果带来误差。
4)计算误差。利用牛顿迭代法求解模型,要求带入的初值无限地接近数值解,而实际计算只能依据经验数据带入初值,因此存在误差。
4 结束语
本文通过结合仿真结果和性能试验,研究了放电室长径比和工况设置对推力器性能的影响规律,得出以下结论:
1)推力器工作效率随栅极电压的增大而增大。当栅极电压高于1 500 V时,效率增加更加显著。
2)随着工质流率增加,推力和推力器效率不断增大。工质流率增大时工质利用率先增大后减小,0.1 mg/s时达到最大;
3)试验研究中,射频功率低于100 W时,射频功率越高,推力器效率越高。为了提高推力器效率,可增大射频功率。
4)随着长径比增大, LRIT-40推力器的性能下降。对于天线圈数固定的推力器,可通过适当地缩短放电室的长度来提升推力器性能。
5)通过对比数值模型计算结果与试验结果表明,放电室均布数值模型可用于射频离子推力器的性能研究。
