不同类型接触面机械零件装配误差的自动计算方法研究*
2021-06-22吴玉光
王 涵,吴玉光
(杭州电子科技大学 机械工程学院,浙江 杭州 310018)
0 引 言
基于蒙特卡罗模拟的公差分析方法是公差分析研究和软件技术中的常用方法。这种方法需要先模拟出实际零件的位置变动;然后,根据实际零件的具体装配接触关系,计算零件几何要素在机器上的位置及其相对于理想位置的变动;最后,利用概率统计方法对大量的变动实例进行统计分析,得出具体的误差数据。
几何要素在机器模型中实际装配位置的计算是非常重要的,由于存在制造误差,参与装配的装配接触面必然偏离其理想位置,这就导致装配接触位置的计算必须采用带误差的几何模型进行计算。
机器零件的公差表示模型作为热点领域受到研究人员的长期关注。一般来说,公差分析可以分为两大领域,即零件层的公差信息分析和装配层的公差关系分析:(1)在零件层的公差表示方面,最先由ARISTIDES R A G[1]使用了边界表示法(boundary representation,Breps),从几何建模的角度提出了漂移公差带理论;ROY U等[2]研究人员进一步对表示公差信息的数据结构进行了优化。(2)在装配层的公差表示方面,BJORKE O[3]最早使用了公差链作线性尺寸的统计公差分析;TSAI J C等[4]提出了公差网络(Tolerance Network)概念,拓展了几何公差和配合信息的表示方式;CLEMENT A等[5]在漂移公差带等理论的基础上,提出了与工艺和拓扑相关的表面(topologically and technologically related surface,TTRS)理论,使用了拓扑相关的功能表面与最小几何基准要素的概念,将零件层和装配层的公差分析很好地结合了起来,这对后来公差表示模型的研究产生了深远的影响。
在分析装配过程的误差时,由于机器在实际装配中具体的配合类型多种多样,为了提供误差分析时的自动化算法,最先需要处理的就是机器中每个零件不同装配形式的识别及归纳问题。HONG J等[6]也意识到了复杂装配中的装配类型对装配公差规格和公差带类型的影响,提出了多色集合理论来描述装配特征、装配约束类型、公差带类型等之间的关系;该理论能处理的零件特征种类较多,但无法处理自由度信息,尚不能直接应用于公差分析领域。钟艳如等[7]提出的公差模型为了处理多种类型装配面的公差计算问题,在特征表面和装配公差之间引入了空间关系,进一步实现了装配公差类型的筛选。葛磊等[8]在文献中分析了同类零件在不同的定位装配方式时,零件制造误差对装配控制目标的影响。朱永国等[9]针对装配过程装配方案改变后,基准变换致使几何公差变化的问题,提出了一种基于公差图(tolerance map, T-Map)的公差转化方法。金少搏等[10]通过装配体约束信息,提取了不同类型的形状特征信息,提出了预测装配的成功率的方法。黎泉等[11]基于TTRS理论对装配表面的类型进行了详细的划分,通过获取零件标注公差信息,建构了装配体的公差网络。
尽管这些研究人员所提出的方法在他们所关注的应用领域均具有适用性,但并不完善,尤其在装配类型的自动化识别和公差设计具体精度影响方面还存在不足。
本文采用控制点变动模型[12](CPVM)来模拟制造误差造成的实际位置变动。该模型基于基本几何要素自由度的理论,在符合GPS标准体系[13]的前提下,既能在零件层面表示基本的公差信息,也能在装配层面获取每个零件的装配类型,按清晰的信息层次将获取公差信息储存在数据结构中,便于与CAD实体模型结合,实现误差传递,完成最终在机器上实际位置的模拟计算。
在合适的零件误差表示模型基础上,可以进一步建立真实机器表示模型。真实机器模型[14]是指在零件层面考虑到零件在制造时产生的几何误差,在装配层面考虑到不同装配类型下,实际具体装配接触因素的公差分析模型:(1)首先,采用CPVM模拟零件的几何误差,采用替代几何模拟零件实际几何的位置变动,即当理想几何要素是平面时,其替代几何是平面,但该平面为实际表面的最外拟合平面;当理想几何要素是圆柱时,其替代几何是圆柱,但该圆柱为实际表面的最外拟合圆柱;(2)然后,按照装配过程中装配基准的不同类型和先后次序,模拟实际零件的装配过程,计算出相应几何要素的可能位置;(3)最后,基于蒙特卡罗模拟方法进行概率抽样,根据大量计算结果求出装配结果的概率分布。
机械零件装配的两个接触面通常具有相同的几何类型,如两个平面、内外圆柱面、内外球面等;但在特殊场合下,也存在不同几何类型的两个接触面进行装配的情况,如传动机械、某些触发和跃动机构以及机械夹具。此时,理论上的接触区域为一个点或者一条线,这种高副接触场合通常接触变形较大,因此研究这种装配体的定位精度计算方法是具有实用价值的。
本文首先建立接触面组合类型集合,在装配接触面仅限于最常见的平面和圆柱面的前提下,根据自由度约束准则,确定正定位零件装配接触面的全部组合形式;然后,重点介绍不同几何类型的装配基准相互接触情况下的装配位置计算方法。
1 机器装配接触面的可能组合类型
为了建立装配位置自动计算的完整算法,需要确定完整的装配接触模型。由于机器中装配信息十分复杂,需要构建一个让计算机易于识别的装配类型表示方法。零件的装配过程可以看作把当前待装配零件通过与已知位置的定位零件进行接触的过程。因此,本文采用自由度约束分析方法来确定机械零件的全部装配接触关系形式。
从自由度分析角度看,装配接触就是约束两个接触面之间的相对位置,即限制相对运动的自由度。不同的装配接触表面类型约束不同的自由度,如两平面接触可以约束3个自由度,而两圆柱面的接触则可以约束4个自由度。此外,两个装配接触几何的类型既可以相同,也可以不同,如在夹具与被加工零件的装配过程中,常见的定位元件包括支承板、圆柱销、V形块、心轴等,这些定位元件的接触面与工件的定位接触面的类型可以相同也可以不相同,不同几何类型的接触面所约束的自由度也不相同。
在装配接触面的几何类型为圆柱面和平面两种情况下,根据装配基准的约束自由度数量,可将机械零件的装配接触形式分为两大类:
(1)第1大类
约束自由度方式为“3—2—1”方式:第一装配基准为两平面“面接触”,约束零件的2个转动自由度和1个平移自由度;第二装配基准为两个接触表面的“线接触”,分别约束1个移动自由度和1个转动自由度;第三装配基准为两个接触表面的“点接触”,只约束剩余的1个自由度。
3个装配基准中,以平面为主基准的各装配接触形式自由度约束情况如表1所示。

表1 以平面为主基准的各装配接触形式自由度约束情况
表1中,双点划线表示定位零件(夹具定位元件)上的接触表面的几何类型及其实际位置,实线表示装配零件(被加工工件)上的接触表面的几何类型及其实际位置,黑点表示当前接触类型在装配体中等效的约束点数,这些接触点的总数量可以对应为约束自由度的数量。
表1中,从第二、第三基准中各选择其中1种方式,排列组合之后可以获得12种装配类型。此外,还有1种特殊的“3—2—1”装配:第一装配基准为两平面贴合,限制当前零件的3个自由度;第二基准为短轴与短孔的装配,约束当前零件的2个平移自由度;第三基准为“点接触”,限制剩下的最后1个转动自由度。
(2)第2大类
装配接触形式以圆柱面作为主基准。第一装配基准为2个圆柱的孔轴配合,孔的内圆柱面与轴的外圆柱面接触约束装配零件的2个平移自由度和2个转动自由度;第二装配基准和第三装配基准分别约束装配零件剩下的1个平移自由度和1个转动自由度。
根据约束自由度方式,这1类装配形式可以称之为“4—1—1”方式。以圆柱面为主基准的各装配接触形式自由度约束情况如表2所示。

表2 以圆柱面为主基准的各装配接触形式自由度约束情况
表2中,第二、第三基准均有4种可能,可以得到16种装配组合类型。需要说明的是,根据功能要求和降低制造成本考虑,零件的装配并不需要限制装配零件的所有自由度。因此,有时并不需要3个装配基准面。
2 不同类型接触面装配的零件位置误差计算方法
2.1 几何要素的控制点变动模型
工程中常用的尺寸链分析法只能做线性尺寸的极值公差分析。漂移模型涉及到了复杂的几何操作,可视化困难,实现难度较大。小位移矢量簇(small displacement torsor,SDT)模型[15]中的计算参数与公差没有一致的对应关系,不能体现公差间的作用。相较之前的分析方法,控制点变动模型(CPVM)能够表示基本几何特征的全部公差类型及其互相作用关系,并且易于实现基准优先关系及基准次序的辨识过程,适用于概率统计的公差分析方法。CPVM用理想几何的尺寸、位置参数来表示实际要素,根据尺寸和位置参数的变动来表示几何要素偏离其理想状态,是一个符合公差意义和公差标准要求的表示模型。CPVM既可以表示零件上各关联要素的实际位置,又可以表示零件的制造误差的具体数值。
本文首先需要介绍圆柱面与平面的CPVM。
2.1.1 圆柱要素的CPVM
圆柱要素CPVM用轴线来表示实际位置,轴线具有4个自由度,即两个垂直于轴线的平移自由度和两个转动自由度。轴线的公差带形状既有圆柱形的,也有四棱柱形的。
圆柱要素的CPVM如图1所示。
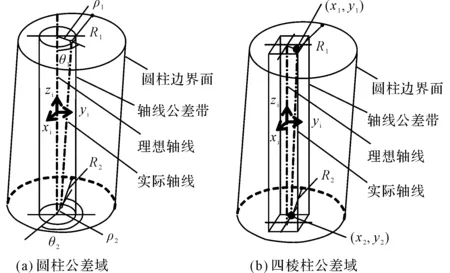
图1 圆柱要素的CPVM
圆柱CPVM中,圆柱轴线的两端点为目标要素的控制点,参数(ρ1,θ1,ρ2,θ2)和(x1,y1,x2,y2)分别为两种公差带的位置误差变量,它们表示了两端点的位置,R1、R2为圆柱两端的半径变量。位置变量的变化遵循圆柱要素位置误差的变动规律,半径变量的变化也遵循圆柱半径的误差变动规律。对于给定的误差变动规律,可以由蒙特卡罗仿真方法对其进行概率抽样,获得6个变量的抽样实例,从而控制圆柱的变动情况。CPVM的位置参数的概率抽样既可以根据一种公差值进行控制,也可以由两种公差进行叠加。即当圆柱要求既标注了方向公差、又标注了位置公差时,可以根据两种公差之间的数值关系分别进行概率抽样,然后加以叠加,从而得到具体的数值。
因此,CPVM既可以模拟存在单一公差形式的几何要素,也可以模拟存在多个公差复合的场合。
2.1.2 平面要素的CPVM
平面要素具有3个自由度,平面要素的控制参数为公称平面规则边界上3个顶点沿平面法线方向的变动量。3个控制点为平面包围盒边界上的任意3个顶点,但当3个控制点的控制参数在公差范围内变动时,根据3个点确定的替代平面会超出公差带,说明3个控制点的变动量还存在制约关系,即3个变动参数的组合必须保证第4个顶点不超出平面的公差带。
平面要素的CPVM如图2所示。

图2 平面要素的CPVM
平面边界包围盒顶点沿平面法线方向(z轴方向)的变动参数分别为t1、t2、t3和t4,图中虚线矩形边界代表平面的公称位置,粗实线四边形边界代表由3个控制点参数(t1,t2,t3)决定的替代几何的一个实际位置,则第4个参数t4取决于前3个参数,其计算方法为t4=t1+t3-t2。平面要素的CPVM既可以模拟单一误差的变动情况,也可以模拟复合误差的变动情况。根据给定的误差分布规律,CPVM可以生成平面的概率抽样实例。
2.2 基于真实机器模型的装配位置计算原理
零件按照装配顺序进行装配时,由于真实机器模型用替代几何模拟了实际要素,考虑到几何要素的刚体假设,零件模型的全部装配接触面之间不再保持理想接触,不同次序的装配接触几何的接触情况完全不同。替代几何只是改变了理想几何的位置,而没有改变其形状。第一装配基准接触为理想接触,由于第一基准装配时没有外界约束,两个零件的第一基准属于自由装配,即第一基准装配依然保持面面贴合。而第二基准装配时必须在保证第一基准面面贴合的约束条件下的装配,由于第二基准替代几何的位置已偏离了理想位置,两者之间的接触位置需要根据实际位置进行计算。因此,在基于真实机器的零件装配位置计算中,第二基准接触位置的计算是其中的难点。
本研究团队已经完成常见的装配情况,本文着重研究了“3—2—1”装配下第二基准和第三基准均为平面-圆柱面接触时的零件装配位置计算方法。
零件在机器中的最终装配位置可以用一个4×4的齐次变换矩阵M4×4来表示,对于不同的装配顺序和装配接触几何,矩阵M4×4中的元素数值完全不同。为了方便计算这些矩阵元素,本文将装配过程分解为4个步骤:
(1)装配零件和定位零件的第一基准面面贴合,将装配零件的第一基准的坐标系与第一定位基准的坐标系重合;
(2)绕轴转动装配零件,使得第二装配基准(圆柱)与第二定位基准(平面)平行;
(3)平移装配零件,使得第二装配基准与定位零件的第二基准相切接触;
(4)保证第二基准相切情况下平移装配零件,使得装配零件和定位零件的第三基准接触。
设4个步骤的坐标变换矩阵分别为M1_mov、M2_rot、M2_mov、M3_mov,这一装配模式的变换矩阵是以上4个矩阵的相乘,即:
M4×4=M3_mov·M2_mov·M2_rot·M1_mov
(1)
其中,M1_mov的计算十分简单,只需把两个坐标系的坐标差的数值分别填入相应的平移分量位置即可。
以下重点介绍第二、三基准分别为平面-圆柱接触条件下,M2_rot、M2_mov、M3_mov的计算原理。
2.3 第二定位基准和装配基准分别为平面和圆柱面的装配接触位置确定原理
第二基准中,定位零件上的定位基准为平面、装配零件上的装配基准为圆柱面影响下装配位置计算原理简图,如图3所示。

图3 第二基准平面-圆柱接触位置计算原理F1A—装配零件上第一基准平面;F1L—定位零件上第一基准平面;C2A—装配零件上第二基准圆柱面;F2L—定位零件上第二基准平面;Fv—辅助的虚构平面λ1—Fv与F1L的交线;λ2—定位基准平面F2L与F1L的交线;l1—圆柱面C2A的轴线;d—坐标原点到λ2的垂线
图3中所示为两个零件在保证第一基准面面贴合后,第二装配基准圆柱面与第二定位基准平面没有接触之前的一般相对位置。
为了不失算法的一般性,假设平面F2L与F1L之间成一般角度,设为β。要保证第二基准装配圆柱和定位平面接触,首先将装配零件绕z轴旋转一定的角度(设为α2),使得圆柱轴线l1平行于第二定位基准平面F2L;然后,沿垂线d方向平移装配零件使得圆柱C2A与平面F2L线接触。
下面分别介绍这两个过程的算法:计算旋转角度α2。由于装配圆柱的轴线l1与定位平面基准F2L在空间中均处于一般位置,要想计算将l1绕z轴旋转使其平行于F2L的角度,需要构造辅助平面Fv。Fv首先应该包含第二装配基准圆柱C2A的轴线l1,并且它与F1L之间的角度为β。计算出Fv与F1L的交线λ1,再计算λ1与λ2之间的夹角,就是装配零件需要绕z轴旋转的角度α2。
第二基准的接触旋转矩阵M2_rot为:
(2)
在这种算法中,一个难点问题就在于辅助平面Fv的确定问题,下面介绍Fv的计算方法。
由于Fv包含l1,而l1的位置在CPVM的信息获取框架中是已知的,只要找到直线外的1点,即可确定平面Fv的位置,关键问题就变为计算出辅助平面Fv上l1以外的第3点P3。
以下根据圆柱轴线l1的位置介绍其计算方法:
(1)圆柱轴线l1平行于第一基准平面。辅助平面Fv上的3个点P1、P2、P3位置及P3的计算方法,如图4所示。

图4 P3计算方法P1—C2A圆柱轴线l1的中点;P2—C2A圆柱轴线l1上的另一点;P3—Fv上l1之外未知的第3个点;在第一基准平面上的垂直投影
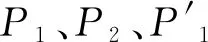


(x-x1)(x1-x2)+(y-y2)(y1-y2)=0
(3)
(4)


若l1处于一般位置,方程(3)可表示为直线的一般方程:
y=k1x+b1
(5)

将方程(5)代入方程(4),方程(4)可以表示为一般方程:
A1x2+B1x+C1=0
(6)

(2)圆柱轴线l1不平行于第一基准平面。辅助平面Fv上的3个点P1、P2、P3位置及P3的计算方法如图5所示。

图5 P3计算方法P1—C2A圆柱轴线l1的中点;P2—C2A圆柱轴线l1与第一基准平面的交点;P3—Fv上l1之外未知的第3个点;在第一基准平面上的垂直投影


根据P1P3与P2P3垂直关系和β的计算式,可得:
(x-x1)(x-x2)+(y-y1)(y-y2)=0
(7)
(8)


若l1的铅垂面处于一般位置,方程(7)与方程(8)相减,可得一条直线的一般方程:
y=k2x+b2
(9)

将方程(9)代入方程(8),方程(8)可表示为:
A2x2+B2x+C2=0
(10)


计算平移距离d2。将拟合圆柱面C2A的轴线与拟合平面F2L均投影到以交线λ2为法线的平面上。在已创建旋转坐标变换矩阵M2_rot的约束下,λ1平行于λ2,并且在该角度上都聚集为一个点;F1A和F1L重合;F2L、C2A的投影为直线。
第二基准平移距离计算方法如图6所示。
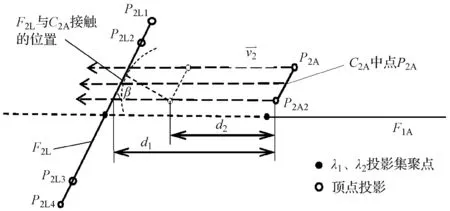
图6 第二基准平移距离计算方法
替代平面基准F2L在边界顶点上构造出4个控制点P2L1、P2L2、P2L3、P2L4;替代圆柱基准C2A的轴线端点上构造出2个控制点P2A1、P2A2。图6中的空心圆圈,即表示这些控制点在所选投影视角中所占据的位置。这一过程的总体步骤为在已有的几何约束下,将第二装配基准圆柱沿一定方向朝第二定位基准平面移动,最终实现圆柱与平面呈线接触。
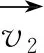
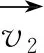

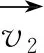
(11)
2.4 第三定位基准和装配基准分别为平面和圆柱面时的装配接触位置确定
经过第一、二基准的限制之后,装配零件只剩下了1个自由度,此时装配零件只能沿某一直线方向自由平移或者绕着某一轴线转动。
根据表1和表2所知:第三基准的几何类型组合有平面-平面接触、平面-圆柱接触、圆柱-平面接触和外圆柱-外圆柱接触4种。由于平面-平面接触的情况在文献[14]中已经介绍过了,这一节只对平面-圆柱接触表面介绍其位置计算方法。本节主要就是根据具体的装配类型,完成第三基准的接触模拟平移矩阵M3_mov的计算,实现对装配零件在剩余自由度方向下微小平移距离的模拟,形成装配零件与第三基准的接触,限制全部的自由度。
第三基准平移距离计算方法如图7所示。

图7 第三基准平移距离计算方法F3L—定位零件上第三实际定位基准平面;C3A—装配零件上第三装配基准实际外圆柱面;当前装配零件的未约束自由度方向
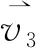
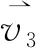
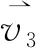
(12)
3 编程实现算法步骤
本文介绍的算法已经在笔者的研究团队研制了公差分析自动化原型软件上得到了实现。该软件总体算法步骤如下:
(1)通过CAD软件提供的编程接口获取装配文档的装配配合信息表,获得整个机器全部装配零件及基准几何信息;
(2)在零件层建立几何要素顶点类,在装配层建立装配零件顶点类,基于CAD软件接口整理机器的信息流,为实现装配层与零件层之间信息的传递提供基础;
(3)基于配合信息表,建立两个核心的数据结构,即装配层上目标零件的装配路径图、零件层上每个零件的几何要素误差传递关系图,作为整个程序的计算流程;
(4)建立坐标系体系,建立各级齐次坐标变换矩阵;
(5)根据不同装配方案对实际位置进行模拟。在具体的分支中,使用CPVM提供的零件、几何要素位置描述信息,根据基准设置的先后次序,考虑实际的接触情况制作接触模拟偏移矩阵,完成实际位置的计算,向基础核心框架中添加理想位置与实际位置的映射,最终实现信息连接;
(6)利用概率统计方法对大量的变动实例进行统计分析,得出具体的误差数据。
4 实例分析
一个包含平面-圆柱装配类型的示例如图8所示。

图8 平面-圆柱装配示例验证
该装配体包含3个零件,有多种装配接触面的类型。其中浅色零件为装配目标零件,深色零件为定位挡板、定位支撑板。其中,定位挡板以一面两孔的方式装配在定位支撑板上,它的两个竖直平面用以定位目标零件。目标零件上的装配基准表面为两个互相垂直的外圆柱表面,通过与定位挡板竖直平面的相切线接触形成几何约束,实现目标零件自由度的约束。
对目标零件来说,具体的装配要求是:长条形的底面作为第一基准,与定位支撑板的顶面接触,面面贴合,控制目标零件的3个自由度;平行于底面的较长外圆柱侧面作为第二基准,与定位挡板的竖直侧面呈线接触,控制目标零件的2个自由度;竖直外圆柱面与定位挡板的侧面呈点接触,控制目标零件的最后1个自由度。
组成装配体零件关键装配面的具体公差信息如图9所示。

图9 装配体公差信息
对话框为原型软件的交互界面及目标要素实际位置的模拟结果,如图10所示。

图10 目标要素实际位置的模拟结果
整个界面总共分7个功能区:左半区域从上至下分成了5个部分,依次为目标显示区、装配路径区、仿真设置区、结果显示区、概率分布区;右半部分是敏感度与贡献率列表区。左1目标显示区表示的信息为用户选择的目标零件名称。左2装配路径区表示的是零件名称及基准信息。
由于装配体零件繁多,目标零件在整个机器中需要一系列中间的定位零件参与定位,与机架建立位置固定关系,会形成1个包含一系列零件信息的装配路径。这是一个交互区,通过前后按钮的选择可以依次查看装配路径中的零件名称及定位当前零件的基准。左3仿真设置区也是1个交互区,用于设置仿真计算时采用概率分布的方式及仿真次数的设置,常见的分布方式有正态分布、均匀分布、偏态分布、三角分布等。左4结果显示区是1个信息输出,用来显示仿真结果的均值和方差信息。左5概率分布区也是1个信息输出区,利用仿真过程中获得的数据,绘制出具体概率分布。
基于真实机器模型的公差分析方法的思想是:先使用CPVM根据几何要素遵循的误差分布规律,自动生成零件实例,即平面和圆柱面的位置变动;然后,根据实际目标零件不同装配类型模拟出具体装配接触关系造成的误差,依次计算零件几何要素在机器上的位置及其相对于理想位置的变动;多次运算后,计算目标要素控制点实际位置相对于理想位置在公差影响最显著方向上的偏移距离,并保存计算结果,形成基础的偏移数组;接着,对偏移数组记录的数值求均值与方差,在结果显示区中进行字符输出;最后,对统计结果进行概率分析,获取偏移数组中记录值所覆盖到的数值范围,并将这个范围分成40个区间,统计每个区间上所落入的样本数量。计算各自概率,在整体界面中以适当的比例对每一个区间的样本统计值进行图形输出。图10为目标平面位置的误差分布情况,因为所有要素的误差都遵循正态分布,装配仿真计算的结果也大致遵循正态分布。
根据装配体中相关零件表面的公差标注信息,可以利用关联表面之间的约束关系模拟误差的积累与传递,计算推导得出目标圆柱轴线理想位置与实际位置之间的距离d,即:
(13)
式中:dx2L—对第二定位基准平面垂直度公差对微小偏移量的模拟;dx3L—对第三定位基准平面垂直度公差数值的模拟;dx3A—第三装配基准圆柱垂直度误差的模拟;dxt2—对目标几何要素位置度误差相对于第二装配基准圆柱方向上实际偏移量的模拟;dxt3—对目标几何要素位置度误差相对于第三装配基准圆柱方向上实际偏移量的模拟。
在该示例中,定位挡板中提供的第二、三基准平面相对于底面基准均由垂直度公差0.1 mm控制,目标零件第二、三基准圆柱相对于本零件上的基准A均由上垂直度公差Ø0.1 mm控制,目标要素在目标零件上的位置由位置度公差Ø0.5 mm控制。
将公差带范围内的极端情况代入公式计算可得:最终误差累计应该处在0 mm~0.92 mm的范围内,使用计算机计算的结果基本处在这个范围内。该结果符合误差的累积规律,证明该方法是有效的。
5 结束语
在装配接触面仅限于最常见的平面和圆柱面的前提下,根据自由度约束准则,笔者提出了正定位零件装配接触的全部组合形式,为实现装配公差分析的自动化创造了条件,便于为每种方案编写计算方法,模拟真实机器中各基准的装配接触,使装配误差的计算更为便捷;
基于控制点变动模型公差分析理论,在CAD环境中模拟零件的基准要素在制造过程中产生的几何误差,以第一基准为两平面贴合,第二、三基准均为平面-圆柱接触时的装配方案为例子,模拟关联表面的制造误差在装配时造成的微小旋转量、偏移量,提出了目标零件在实际装配接触影响下,目标要素在机器中的位置的计算方法;并通过案例证明了方法的有效性。
当前方法仅考虑了平面、圆柱面作为装配基准情况的装配位置计算,更多的几何类型的装配接触情况、各种欠定位情况下的装配位置计算方法还需要在之后的研究中进一步探索,以完善方法的通用性。
