一种钣金折弯过程抓取点轨迹计算方法的研究
2021-06-22许路佳范立成张凤明
许路佳,范立成,张凤明
(苏州大学 机电工程学院,江苏 苏州 215000)
0 引言
在钣金折弯领域,国外如ABB、西门子都有钣金折弯离线编程系统,已经实现了在实际生产中完全自动化加工[1]。而国内钣金生产领域起步较晚,多数企业仍未实现自动化,机械臂配合钣金折弯过程多运用经验法,但此方法往往需要进行多次调试,其过程耗时、耗材。查健[2]通过建立模型方法,计算得到抓取点在折弯过程中与初始点的位置关系,但未考虑折弯过程中钣金长度变形,在厚件钣金折弯中会出现较大误差。张如华等[3]通过建立多种模型方法得到指定点轨迹与折弯角度之间的关系,但未与上模工进距离建立联系。本文建立了折弯过程的数学模型,对抓取点位置进行了计算与分析,并通过仿真进行了验证。
1 钣金折弯过程分析


图1 钣金折弯中性层
2 钣金折弯过程的抓取点空间轨迹公式推导
钣金折弯的数学模型如图2所示。钣金厚度|DD″|为s,折弯机上模与待折弯钣金件接触于E点,下模的槽口边界分别为F、I点,间距为2l。建立以O点为坐标原点的坐标系,x、y轴方向分别为OF、OE,A0为机械臂末端吸盘与钣金的接触点,在折弯过程中移动到位置A(xA,yA),折弯过程中中性层A′B′C′D′在折弯过程中长度不变。中性层系数取k,机械臂与钣金接触点A0距离钣金折弯处长度为b,在折弯过程中折弯半径|KC″|为r。钣金折上模工进深度(即EC″的长度)为a,具体计算过程如下。
由数学关系可知,ΔOFG≅ΔBKG,设∠OFG=∠BKG=θ,则:
(1)
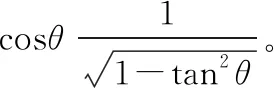
(2)
(3)
曲线B′C′的长度为(r+ks)θ,可求得
|AB|=|A′B′|=b-(r+ks)θ
(4)
由图2可知,|KB|=r+s=m,坐标系中C″(0,s-a),K(0,s-a+r),B(xB,yB),其中:
xB=msinθ,yB=m-a-mcosθ
(5)
做辅助点H,∠AHB=90°,∠ABH=∠OFG=θ,可得
|AH|=|AB|sinθ,|BH|=|AB|cosθ
(6)
已知B(xB,yB),可得A(xA,yA):
(7)
通过以上计算得到了A(xA,yA)和折弯机上模工进深度a的数学函数关系。
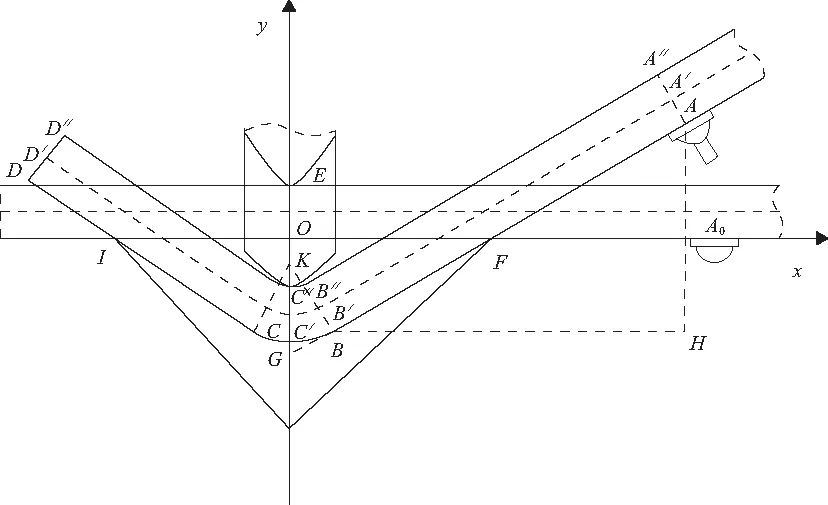
图2 钣金折弯过程数学模型
3 仿真验证
为验证计算结果的正确性,采用实践中常用数值,设待折弯钣金材料为不锈钢,上模尖点半径为0.5mm,2l=20mm,b=180mm,s=3mm,根据折弯经验,6mm以下钣金折弯半径可取自身厚度,即r=3mm。取不锈钢中性层系数k=0.4,计算可得当折弯角度为90°时,a=7.5mm,取折弯机上模工进距离a为自变量,得到函数关系曲线如图3所示。

图3 各项参数与工进距离函数关系
取相同的参数值在Ansys中进行仿真,并将结果与仿真结果进行对比,如图4、图5所示。通过结果对比发现,建立数学模型得到的计算结果与仿真结果有较好的契合性,由于实际的钣金折弯过程中,变形并非完全按照建立的数学模型进行,同时折弯机下模存在较小圆角,不可避免造成理论计算与仿真结果存在误差值,但机械臂末端吸盘与钣金之间并非刚性接触,允许一定误差的存在。通过与仿真结果的对比,在折弯过程中A点的横、纵坐标随工进距离的结果误差值先增大后缩小,整体误差在1.5mm以内,空间轨迹结果有较好的重叠性,从而验证了数学模型与计算结果的正确性。
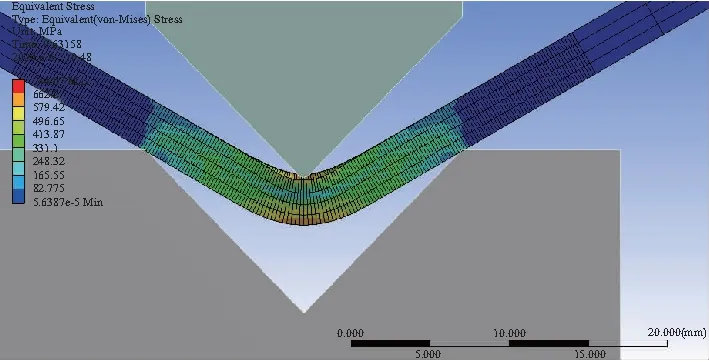
图4 钣金折弯过程仿真
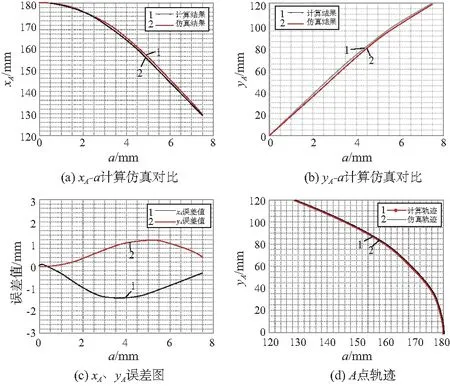
图5 计算与仿真结果对比
4 结语
本文利用钣金折弯过程中中性层长度不变的特性建立了钣金折弯数学模型,并对折弯过程进行仿真分析,仿真与计算结果的对比显示,两者表现出较好的契合性,验证了所建立的钣金折弯过程数学模型与计算结果的正确性,同时对出现的误差原因进行了分析,为钣金折弯过程机械臂末端路径规划提供了理论依据。
