冲击载荷和随机振动条件下电池箱响应分析

韩明轩，张洪信

(青岛大学 机电工程学院，山东 青岛 266071)

0 引言

对于纯电动汽车的电池箱进行结构仿真可以快速分析出电池箱的安全性能。动力电池作为电动汽车的重要储能部件，其电池箱在高温、振动冲击下能否正常运作显得格外重要，它的使用安全会直接影响汽车整车的安全与寿命。目前，电池箱的响应数值分析通常要考虑的是箱体动强度分析[1-2]。最近几年，很多研究人员通过有限元分析来检测电池箱的安全，并对电池箱做了大量的工作。安徽某公司的赵久志等人对动力电池总成的壳体结构建立了三维实体模型，之后将三维模型导入 Hypermesh 中，建立动力电池壳体结构的有限元模型[3]。XIA Yong等人对锂离子电池箱的底部碰撞进行了综合研究，提出了对电池箱底部碰撞的试验方法，建立了动力电池箱在有穿孔过程中的冲击过程、裂纹传播和电池单体的局部失效模式，研究电池包底部碰撞涉及到的参数，以提高底部碰撞安全性[4]。吉林大学的李明秋基于 ANSYS Workbench 平台建立动力电池箱的三维实体有限元模型，结合极限和实际工况，对电池箱进行机械冲击分析、模态分析和随机振动分析，根据分析结果改善了结构设计[5]。我国每年交通事故的死亡人数高达数万人，因此有必要加强对电动汽车交通事故形态的研究并探讨相应的对策。

本文运用类似的方法对电池箱进行有限元分析，在电池箱设计上考虑电池箱机械冲击工况和振动工况。动态冲击工况和振动工况对应的国标为GB/T31467.3—2015《电动汽车用锂离子动力蓄电池包和系统第3部分：安全性要求与测试方法》。首先对静态冲击工况应用静力学分析，其计算效率较高，根据仿真结果可对其结构性能进行预测，以达到改进优化设计方案的目的。振动工况根据国标规定需对电池箱进行z、y、x方向即垂向、横向、纵向的振动分析。通过对电池箱各个方向的检测，判断满足屈服应力的条件下电池箱是否安全。

1 电池箱有限元模型建立

1.1 几何模型的建立

根据企业所给研究对象的二维参数，将电池箱的实际结构进行简化，并运用CAD软件进行三维的建模，这样会比在有限元软件中建立模型更加高效且操作简便，见图1。

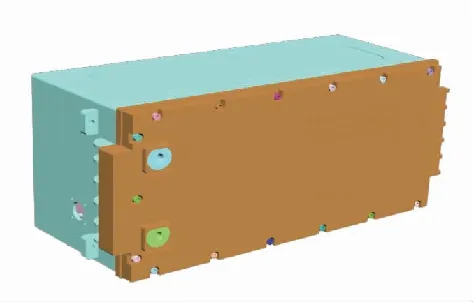
图1 电池箱CAD视图

1.2 电池箱有限元模型建立

1)建立三维模型，将文件转成IGES格式，并将图形导入到Hypermesh中，开始有限元分析。

2)对几何模型再次进行清理与简化。有限元模型是对实际模型的近似模拟，只要在不影响电池箱整体性能和力学性能的情况下，可以删除并清理一些电池箱上比较难处理的地方，这样不会影响电池箱在有限元测试中的应力变化。

3)对模型进行显隐化并抽取中面。将模型导入Hypermesh中，把模型分为两大部分，一个是下壳体，另一个是上盖。分别将这两部分显隐化并对它们抽取中面，再对其进行前处理。

4)对下壳体进行网格划分。为了提高计算的精准性，在单元类型的选择上通常选择四边形为主、三角形为辅的方法进行划分，并且希望误差较小。选择单元网格边长为5mm的四边形进行划分。再次隐藏下壳体并对上盖进行实体网格划分，同样选择边长为5mm的四边形进行划分，修正网格并且得到网格较好的网格划分。图2给出了已经划分完网格的电池箱。

图2 电池箱网格划分

5)对网格质量进行检测，通过表1的单元质量检查规范，发现电池箱的网格划分良好。

表1 单元质量检查规范

6)材料的选取。本文中电池箱选取的材料为A3钢，其具体的材料属性如表2所示。

表2 材料属性

2 机械冲击下工况分析

2.1 分析过程

在Optistruct求解器下施加25G重力场，方向是垂直于地面向下的，并且创建GRAV类型载荷集。除去重力场以外，各方向不加以外力，其中N1、N2、N3代表x、y、z3个方向。G为比例参数，实际载荷大小为G×N，这里的25G重力场依据国标动态冲击最大值加载。

2.2 机械冲击结果

将用力结果导入后处理Hyperview中。电池箱在冲击载荷下的应力云图如图3所示(本刊黑白印刷，相关疑问咨询作者)。电池箱所受机械冲击的最大应力处于电池箱y轴方向的下壳体最上端，最大应力为39.3MPa。在电池箱屈服应力内，电池箱未出现破损现象。

图3 机械冲击下电池箱1σ应力云图

3 随机振动下工况分析

3.1 振动理论

根据振动理论可知，电池箱结构在线性范围内，每个运动微分方程都具有特定频率的自由振动，N个运动微分方程组合后的频率即为该结构的固有频率，其振动形态可由结构模态振型和模态阻尼来表示[6]。n个自由度随机振动的计算公式为：

(1)

(2)

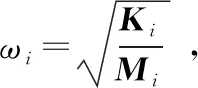
(3)

式中ξ和γ分别表示阻尼比和阵型参与系数。同时可得模态向量ui在时间域内的解为

(4)

式中hi(τ)为脉冲向量函数，且ui和X(t)的关系为

(5)

将式(4)和式(5)联立，得

(6)

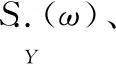
(7)

由于公式计算过于复杂，简化公式可得

(8)

同时得到响应均方值：

(9)

电池箱受到振动以后，所受应力满足零均值高斯分布，求得其标准差，从而获得响应值的分布概率[7]。

3.2 分析过程

首先加以约束。在电池箱两侧4个固定孔处分别加以约束x、y、z3方向的平动自由度和转动自由度。除此之外加以加速度激励，激励方向为电池箱垂向方向，即垂直于路面，大小为9 810mm/s2，并在Load collector中添加一个幅值为1的正弦曲线，最后将它们全部导入Rload1中，使激励和加载曲线进行组合。同理分别设置对电池箱横向方向和纵向方向的Load collector，并定义RANDOM分析步，与箱体垂向方向的振动工况步骤类似。

参考 GB /T 31467. 3—2015《电动汽车车用锂离子动力蓄电池包和系统第3部分: 安全性要求与测试方法》中的振动试验要求，对汽车前部电池箱的x、y和z轴3个方向进行稳态随机激励，其PSD值如表3所示。电池箱的x、y和z轴3个方向加速度的均方根值分别为0.96g、0.95g、1.44g(g为重力加速度)。

表3 加载激励PSD值

3.3 随机振动结果

求解分析后，将Optistruct应力结果导入后处理Hyperview中，得到在垂直方向工况下电池箱箱体的最大应力，即1σ应力是12.52MPa，3σ应力是37.56MPa，应力值较小。箱体纵向方向振动工况输出设置与箱体垂向方向振动工况步骤类似，得到电池箱箱体的最大应力，即1σ应力是22.46MPa，3σ应力是67.38MPa，整体应力水平较低。同理箱体横向方向也是按照此步骤进行处理，得到1σ应力为7.447MPa，3σ应力为22.341MPa，整体应力水平较低。3个方向应力均远小于屈服应力235MPa，3个随机振动如图4-图6所示。

图4 垂向激励下电池箱1σ应力

图5 纵向激励下电池箱1σ应力

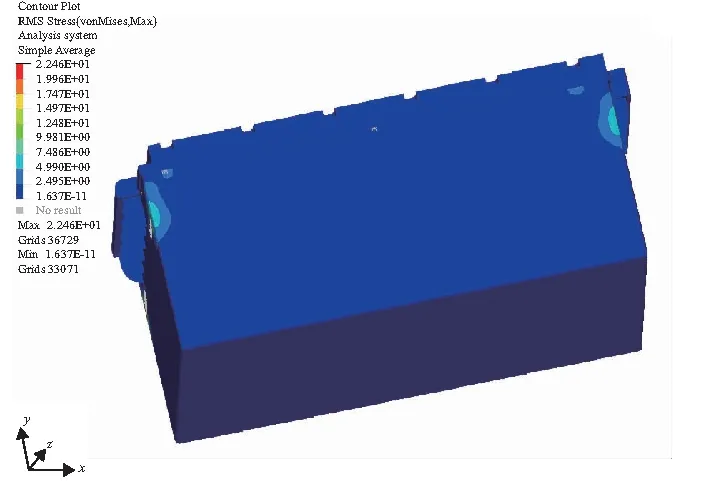
图6 横向激励下电池箱1σ应力

4 结语

电池箱的安全性能决定整车的安全性。由于电池箱的内部比较复杂，受力分析也很复杂，所以本文基于有限元分析的方法对某企业的电池箱在随机振动以及机械冲击下进行分析，运用三维软件进行三维几何建模，分析电池箱内部结构，将模型导入Hypermesh中，在不影响分析结果的情况下对电池箱进行简化，抽取中面，划分网格并定义材料属性，从而建立有限元模型。在机械冲击的工况下，电池箱所受的应力远小于屈服应力。对电池箱的垂向、横向和纵向分别做随机振动的仿真实验，得到3组仿真所受到的应力均小于材料屈服应力的结果，说明其结构可靠，可以完整通过随机振动实验，并为汽车在随机路面下随机振动提供了计算方法[8]。