基于特征矩阵优化与数据降维的文本聚类算法
2021-06-22卢佳伟
陈 玮,卢佳伟
(上海理工大学光电信息与计算机工程学院,上海200093)
引 言
文本文档作为互联网舆情信息的主要载体,一直是数据信息时代的研究重点,能否监控并处理好这些文本信息是实现社会和谐发展的重要前提。伴随着自然语言处理技术的不断发展,各类文本信息处理的技术愈发完善,对舆情信息的处理也越来越高效,其中文本聚类是文本挖掘、机器学习和模式识别领域最具代表性的技术之一。作为一种无监督学习的方法,文本聚类在数据分析处理上承担着重要的角色,通过将大型的文本文档分解为具有各类特征代表的文档子集,从而实现对文档的管理与监控[1]。
在文本数据处理的过程中,向量空间模型(Vector space model,VSM)是一种被广泛采用的模型,模型内每一个词都被认定为文档的一个特征从而映射到向量空间中[2]。文本文档一般会形成一个高维度的向量空间模型,每一个维度依次对应一个权重值,初始文本文档通常包含高维信息和噪声信息特征,后者以其非相关性、冗杂性和分布散乱性的特点成为聚类工作中一个处理难点[3]。特征选择的主要目的是确定文本中最具代表性和高辨识度的特征。传统文本特征的选择处理有3种方法:基于文档频率(Document frequency,DF)的特征选择、基于词频(Term frequency,TF)的特征选择和基于文档频率和逆词频(Term frequency inverse document frequency,TF⁃IDF)的混合特征选择,这些方法主要依靠词频统计来完成矩阵特征的提取[4]。文献[5]通过确定词对文本密集度的贡献来评定该词的价值,从而找出不损失文本有效信息的最小特征词语集,创造出更为合理的权重计算方案。文献[6]提出一种多标记的属性约简特征选择方法,将粗糙集应用于多标记数据的特征选择中,定义了一种领域粗糙集的下近似和依赖度计算方法。上述方法都通过引入其他属性对矩阵做出相应调整,从而产生更为明显的特征子集,但往往忽略了特征矩阵内在的影响。本文提出一种自适应的特征矩阵,依靠自身的词频率分布来产生特征权重计算方案,在改进传统的TF⁃IDF算法的同时,使得生成的特征矩阵具有更好的分布性。
文本矩阵空间的高维性仍然是一个终极挑战,文本文档集合一般包含成百上千个文本特性,文本集群因此变得非常复杂。一般来说,文本聚类性能受到文本文档维数的影响,尽管高维的数据包含的信息很多,但是往往会降低文本集群的准确性,通常需要采用一定的降维手段对其进行处理,最终实现聚类性能的优化[7]。从技术上讲,有效的降维应该做到消除无用的文本特性,即不必要的、不协调的和嘈杂的文本特征等等,保存内在信息,从而显著降低文本特征空间的维数,常用的降维方法为主成分分析法(Principal component analysis,PCA)[8],但是当数据维度十分庞大时,此时PCA降维后生成的矩阵非常不准确。文献[9]将高维数据泛化为新的距离表达式,并且结合信息熵构造出新的特征评价函数,评价每一个维度的信息量来消除冗余特征后再聚类,这样最大限度地保留了数据信息,同时完成了降维处理。文献[10]在此基础上结合PCA降维算法,将PCA算法中映射到低维空间的方差最大化标准改进为一种基于特征度量的信息熵标准,使得降维后的数据具有更好的分布特性。本文在此两者基础上提出一种基于联合熵特征度量的标准,即对所有特征计算同时发生时的信息熵,进一步保留重要的矩阵信息,从而使得降维后的数据具有更好的完整性。
1 特征矩阵优化
随着文档的复杂性与其内容的多变性的增加,文本向量化后形成的矩阵变得越来越稀疏,并且特征项愈发不明显。因此,本文提出一种新的加权方案ALFW(Adaptive length frequency weight)来获得一个加权特征项得分,并通过这个权值来有效地区分信息性和非信息性文本特征,以此来提高文本特征选择的效果。TF⁃IDF是目前的一个标准权重方案,着重体现了词频对特征矩阵的影响[11],具体如式(1~3)所示。


式中:d j表示一个文本,nij代表某词在文本d j中的出现次数,文本d j中每种词条的出现总数使用表示,|D|代表所有文本的总数,|{j:ti∈d j}|表示包含词语ti的文本数目。
新提出权重方案ALFW的主要目的是在此基础上合理地突出特征项以及优化非信息特征对矩阵的影响。ALFW的建立主要依靠以下3个因素:首先引入si变量削弱了逆词频对整个文档的影响,其次,考虑到一篇文档中并没有考虑其所有特征项频率对权重方案的影响,因此si变量的添加也对选择数量较少的信息特征起到了帮助;最后maxtf(i)是一个主要的因素,它对分配一个良好的词频权重分数起着至关重要的作用。ALFW的引入使得文本特征选择技术更加容易地找到新的信息特征子集,这也将最终提高文本聚类算法的性能。
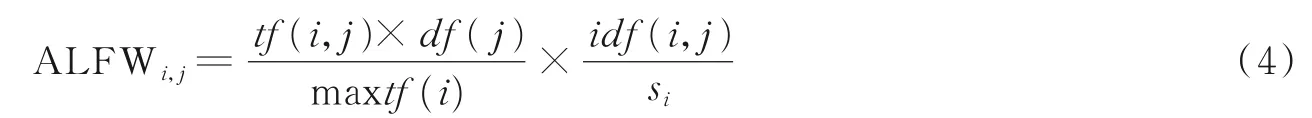
式中:maxtf(i)表示文档i中最大的特征频率值,si表示文档i中的特征项被选择次数不为0的特征数之和,df(j)代表包含特征j的文档数。
表1为特征频率分布矩阵,表示10个特征项在8篇文档中的分布情况,表2和表3分别给出了在TF⁃IDF算法和ALFW算法下生成的特征矩阵,对比矩阵进一步说明了ALFW与经典方案(TF⁃IDF)进行比较时的优势,此示例是在8个带有10个特征权重的文档上完成的。从表2,3中可以明显看出,与经典的权重方案(TF⁃IDF)相比,本文提出的ALFW权重方案更有效地区分了文档的特征。表2中对于文档2中的第10个特征,TF⁃IDF给出的权重显然过大(2.709),而经过ALFW权重方案处理后得到了一个合适的权重(0.043)(见表3)。同时,可以看到表2中的2,3,4特征项在各个文档中都表示出相同的权重,这说明文档级别的特性没有体现出来,而ALFW在这3个特征项中均给予了不同的权重值,使得矩阵的特征区分更加明显。
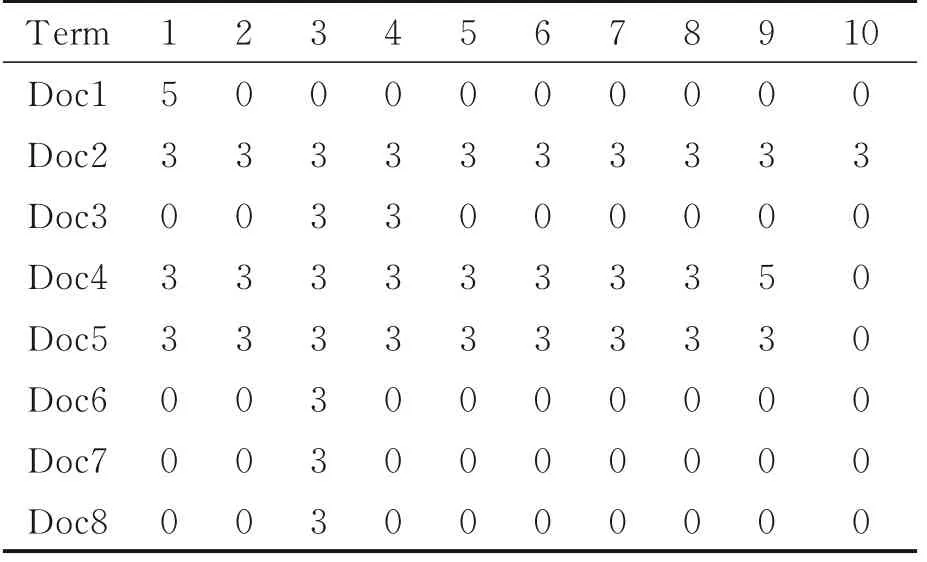
表1 特征频率矩阵Table 1 Fr equency of char acter istic matr ix

表2 TF⁃IDF矩阵Table 2 TF⁃IDF matrix

表3 ALFW矩阵Table 3 ALFW matrix
2 基于联合熵标准的PCA降维处理
传统的PCA算法在处理稀疏的高维数据时,结果往往不太理想,文献[12]提出对传统PCA算法进行改进,提出一种利用信息熵对数据进行特征筛选,再采用PCA进行降维处理的算法。本文在此基础上提出一种基于联合熵标准的PCA降维算法(United entropy PCA,UE⁃PCA)。信息熵的定义如式(5)所示,信息熵是一个随机变量H(X)所有可能情况的自信息量的期望。信息熵表征了随机变量所有情况下的平均不确定度,有

信息熵推广到多维领域即为联合熵,具体公式如式(6)所示。采用联合熵的好处在于在降维时不再单一的关注自身随机变量包含的信息,可以与其他变量联合产生新的信息量,从而使得特征信息更加完整地保存,反映出原高维稀疏矩阵数据的更为真实的分布情况,更好地服务于文本聚类算法,即
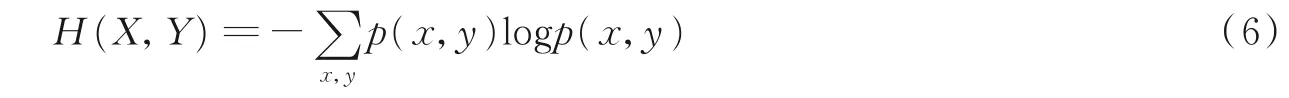
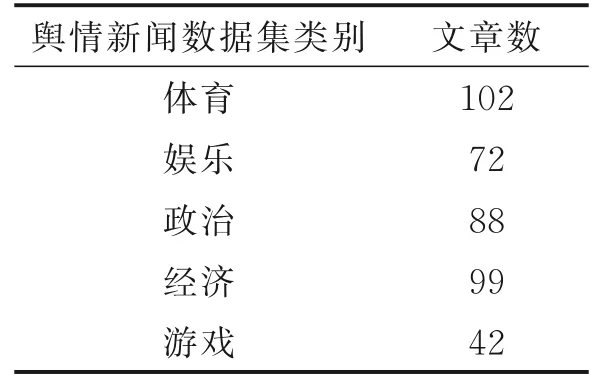
同时引入文献[10]中的属性空间概念,属性空间与数据空间的区别在于属性空间中的点是抽象空间具象化,即属性成为了空间中的点[10]。给出一个维度为p的高维数据集合D={x1j,x2j,…,x ij,…,x nj}(0 将上述属性空间与联合熵进行组合,则形成属性空间联合熵(United entropy,UE)。属性空间联合熵的定义如下。 给定一个属性空间T={t1i,t2i,…,tji}(0 结合特征值得到UE⁃VAR(United entropy⁃variance)标准,有 式中:UE T为选取的属性特征集合的属性空间联合熵,var为集合中每个特征属性对应的特征值的和,用这个特征值的和代替方差也可反映出数据的波动情况。λ1和λ2为经验参数,根据方差和联合熵的比例来调节之后选择0.7作为两个参数的值。 基于以上分析,本文提出UE⁃PCA算法的具体步骤如下。 算法:UE⁃PCA 输入:初始数据集D 输出:降维后数据集W begin 输入数据集D=M n*p(矩阵M包含n个p维的数据)=(x()1,x()2,…,x(m)) 去中心化处理 计算协方差矩阵Dcov 求特征值λ与特征向量,并确定降维后的维度r值 实验仿真的流程如图1所示。首先对数据集进行预处理,包括去停用词、分词、此行过滤等步骤,随后采用VSM向量空间表示并使用ALFW权重方案来建立特征矩阵,再由基于联合熵标准的PCA算法降维处理后运用K⁃means算法进行最终的聚类验证。 图1 算法流程图Fig.1 Algorithm flowchart K⁃means是一种迭代求解的聚类分析算法,通过随机选取k个对象作为初始聚类中心,随后计算每个对象与其他子类聚类中心的距离,将每个对象分配给距离它最近的聚类中心。此时,聚类中心与中心的其他被分配点就成为一个类簇。对象的每次更新,聚类中心也会随着当前聚类情况而被重新计算,直到收敛到某个值或达成某个终止条件[13]。K⁃means算法以其简捷性、高效性而被广泛运用于聚类领域,在处理大数据集时,该算法可以保证良好的伸缩性和高效性,因此,本文选用其作为聚类数的判定手段,采用轮廓系数作为聚类效果的验证方法。 轮廓系数是一种聚类效果的评价方式,通过结合内聚度和分离度来完成评估[14]。其计算公式为 式中:a(i)表示样本i到同簇其他样本的平均距离,也称之为内聚度,内聚度越小代表类聚合的效果越好;b(i)表示样本i到其他簇的簇的所有样本的平均距离,即分离度,分离度越大表明类簇之间的划分越明显。s(i)的取值范围为(-1,1),聚类的最终效果由此评判,值越接近1表示聚类效果越好。 本文数据集选自THUCNews文本数据集。THUCNews是根据新浪新闻RSS订阅频道2005—2011年间的历史数据筛选过滤生成,包含74万篇新闻文档(2.19 GB),均为UTF⁃8纯文本格式,该数据集分为体育、财经、房产、家居、教育、科技、时尚、时政、游戏和娱乐10个类别。本文从其中随机选择10 000篇,每类1 000篇作为实验测试数据集。在仿真实验之前,需要对文本文档作预处理,即停用词过滤和分词操作,相应地使用jieba分词工具和中文停用词表完成。 除此之外,本文另外爬取2018年10~12月的网络新闻数据共计403篇短文进行舆情聚类实验,详细的数据集信息如表4所示。 表4 数据集信息Table 4 Data set 本文实验选择4种算法模型进行对比,分别为PCA降维算法+TFIDF算法+K⁃means聚类算法的传统组合算法、PCA降维算法+ALFW特征矩阵+K⁃means聚类算法的组合、文献[10]提出的算法以及本文算法(K⁃means+UE⁃PCA+ALFW)。 图2 大样本数据集算法轮廓系数对比图Fig.2 Comparison of silhouette coeffi⁃cient of large sample data set algo⁃rithm 表5 大样本轮廓系数对比表Table 5 Silhouette coefficient comparison table of big data set 从图2可以看出随着类簇数的增加,轮廓系数曲线逐渐上升,当达到区间[8,10]时,各个算法呈现的轮廓系数曲线都开始逐步下降,说明此时聚类时的内聚度与分离度之间达到一个平衡的状态,也是聚类最佳的状态,超过这个区间之后,轮廓系数评价值大幅下降。从表5可以看出采用传统的K⁃means+PCA+TF⁃IDF组合算法模型、K⁃means+PCA+ALFW组合算法模型、文献[10]算法和本文算法分别在类簇数为9、10、11、10时达到最佳聚类状态,而实际上的标准类簇数为10,从而可知本文算法正确完成了聚类。观察4种模型算法在类簇数为10时的轮廓系数得分,本文算法也取得了最佳的0.673得分。同时对比K⁃means+PCA+TF⁃IDF组合算法模型和K⁃means+PCA+ALFW组合算法模型,可以看出后者取得了更好的效果,这也进一步验证了ALFW矩阵对聚类结果优化的有效性。 此外,本文在自主爬取的5类小样本数据也进行了仿真实验,实验结果如表6和图3所示。同样地,本文算法依旧取得了最佳的轮廓系数评价(0.724),在小样本中更加体现出了算法的优劣性。 表6 小样本轮廓系数对比表Table 6 Silhouette coefficient comparison table of small data set 图3 小样本数据集算法轮廓系数对比图Fig.3 Comparison of silhouette coeffi⁃cient of small sample data set al⁃gorithm 本文针对传统的TF⁃IDF特征权重矩阵做出改进,提出一种基于ALFW特征权重方案的特征矩阵,使得矩阵的特征项具有更好的分布性,对后续聚类算法的性能进行了提升。高维数据的稀疏性通常会严重干扰到聚类算法的效果,因此,本文提出一种基于联合熵标准的PCA降维算法,使得特征信息在完整保存下来的同时,过滤掉大量上下文无关特征信息,更好地反映出原高维数据特征矩阵的真实性。基于上述两项改进,本文提出的基于特征矩阵优化与数据降维算法(K⁃means+UE⁃PCA+ALFW)最终在4种算法的评估中取得最佳效果。
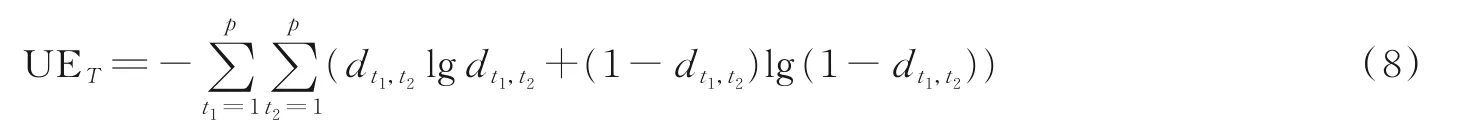



3 实验仿真及分析

3.1 评价标准

3.2 数据集
3.3 实验结果分析




4 结束语
