基于粒计算的多粒度数据分析方法综述

李金海，王 飞，吴伟志，徐伟华，杨习贝，折延宏

（1.昆明理工大学数据科学研究中心，昆明650500；2.昆明理工大学理学院，昆明650500；3.浙江海洋大学信息工程学院，舟山316022；4.浙江省海洋大数据挖掘与应用重点实验室（浙江海洋大学），舟山316022；5.西南大学人工智能学院，重庆400715；6.江苏科技大学计算机学院，镇江212003；7.西安石油大学理学院，西安710065）

引 言

多粒度数据分析是大数据研究领域中的重要课题，它基于多粒度思想对数据进行多角度、深层次的分析与处理，以解决现实中特定复杂数据的知识发现与表示问题［1⁃4］。多粒度数据通常是对数据进行不同粒化得到的多个侧面认识，它的显著特点是数据可以在多个粒度空间进行呈现［5］。多粒度数据广泛存在于人们生产生活中，比如考试成绩有百分制也有等级制，电子地图能够显示到市县一级也能够进一步细化到乡镇一级甚至村落一级，论文可以按影响因子排名也可以按分区明确其大致的等级。也就是，人们会根据自己的实际决定在哪个层面进行数据分析与处理比较合适，这也是人们解决问题时比较擅长的方面［6］。实际上，出现这种现象是由于数据在不同粒度层面上进行显示的代价和效果存在差异导致的［7］。众所周知，数据在粗粒度层面上进行呈现的代价小，因为粗粒度一般意味着数据提供的信息量较少，而数据在细粒度层面上进行呈现的代价大，因为细粒度一般意味着数据提供的信息量较大。有趣的是，人们往往是从粗粒度数据开始不断提高对粒度进行细化的要求，即对数据粒化的认识是一个渐进的过程，下一次认知会受上一次认知结果的影响，这完全符合人们认知事物需要经历不断修正自我判断的心理过程［4，8⁃12］。除了日常生活中采集存储到的多粒度数据，在很多科学研究中也会得到各种各样的多粒度数据，当然不一定把它们全部都显示出来，因为大部分属于解决问题时形成的中间信息，比如当数据粒化时所采用的关系、函数或约束条件逐步变强时，它们对论域的粒化程度会越来越细，从而产生多粒度数据以便更好地解决问题［13⁃14］。其原因是对论域进行粒化通常能够带来计算上的便利以及结果的表示会更加简洁等诸多好处，而本质则是提高解决问题所需的解空间的维度［15］，使得解空间的搜索范围相对变小（即粒度变大使得总的粒度个数变少），这种粒度转化思维尤其适用于完成大规模数据分析任务。

目前，已有一些比较成熟的粒计算方法基于不同的需求对多粒度数据进行研究，常见的研究思路包括并行多粒度知识发现、序贯多粒度知识发现、多粒度认知以及多粒度学习等。这些粒计算方法来源于多个研究领域，比如商空间理论［6，15］强调复杂问题通过不同的粒度空间之间的映射关系可以找到合适的解决途径，即求解商集和商结构的过程；序贯三支决策［16］通过粒度粗细变化对目标概念的边界域持续产生的影响解决三分类问题；多粒度粗糙集［17⁃18］通过多个二元关系（由多个属性子集确定）的逻辑“且”“或”组合运算对目标概念进行近似，即融合局部知识得到各种各样的全局知识；多尺度数据分析模型［5］讨论知识在不同尺度下的关系以及在给定尺度好坏评价标准的情况下如何选择最优尺度，使得知识表示与获取能够在最优的粒度空间中实现；多粒度形式概念分析［19⁃20］通过属性粒度树及其剪枝实现多粒度数据的跨粒度层知识发现等。实际上，对于多粒度数据，不同的研究领域所采取的研究思路是不一样的，因为它们最终要达到的目的有所不同。本文不讨论这些粒计算方法之间存在的区别与联系，而是以多粒度数据分析为研究对象，归纳总结当前粒计算领域中已开展的多粒度数据分析工作，并提出其存在的问题，为促进该领域的进一步研究与发展提供理论参考。

1 基于粒计算的多粒度数据分析方法

本节对基于商空间理论、序贯三支决策、多粒度粗糙集、多尺度数据分析模型和多粒度形式概念分析等的多粒度数据分析研究进行综述。这里不包括对粒计算的基本概念、核心思想以及传统研究方法的介绍，感兴趣的读者可以参考文献［21⁃27］以了解粒计算及其最新的研究动态。

1.1 基于商空间理论的多粒度数据分析

假设用三元组(U，f，T)描述一个复杂问题，其中U代表问题的论域，f(•)代表论域的属性，T代表论域的结构。商空间理论［6］主要研究如下形式的问题：在给定关系R（可以多个关系）的情况下，将论域U自然投影到商集[U]，同时伴随着论域的属性f和结构T也自然投影到商集[f]与[T]，那么原问题(U，f，T)与商空间([U]，[f]，[T])之间关于问题的解存在哪些关系？当给定多个关系Ri(i=1，2，…，k)时，商空间([U]i，[f]i，[T]i)之间关于问题的解又存在什么关系？商空间理论的大致框架如图1所示，它的核心思想是探讨一个复杂问题如何通过粒化分析与运算能够在粗粒度世界中得到解决，以降低求解问题的复杂性。需要指出的是，保真原理和保假原理为粗细粒度世界中的解进行相互推理起到了关键作用，详见文献［6，15］。

图1 商空间理论构架Fig.1 Theoretical framework of quotient space

自商空间理论提出以来，已受到粒计算领域的专家和学者的广泛关注与研究。文献［28］通过模糊等价关系将精确粒度下的商空间理论推广到模糊粒度环境中，在模糊粒度计算、粗糙集和商空间三者之间搭建起联系的桥梁，为交叉融合研究做出了贡献。文献［29］利用互联网中的路由选择和称球游戏论述了商空间理论在解决复杂问题时使用的一般粒度描述过程。文献［30］建立了小波变换与商空间近似之间的联系并应用于信号的多分辨率分析。文献［31］讨论了图像分割的商空间理论，主要思想是对图像进行分层提取与合成以充分利用图像的各种局部特征信息，且仿真实验表明该方法对复杂纹理图像进行分割的效果较好。文献［32］基于模糊商空间通过模糊相似关系和归一化距离得到了分层递阶结构聚类分析方法。文献［33］于2009年从商空间的构造、商运算、商约束、商近似、模糊商空间及其应用等方面对商空间方法进行了综述。文献［34］利用商空间的粒度世界观并结合模糊相容关系簇的同构思想解释了模糊集各种主观定义的合理性。文献［35］在经典的商空间中引入时间维度以建立信息动态处理的数学模型，然后借助高维上的静态模型解决低维上的动态商空间问题。文献［36⁃37］对不同商空间之间的合成与分解得到的新的商空间做了比较研究，获得了商运算的若干重要性质。文献［38］针对整个网络节点之间的最大流问题讨论如何利用商空间理论减少计算点对最大流的总次数。文献［39］利用商空间粒度分析提出了改进的覆盖算法，布置在Spark上运行以实现并行大规模计算，并成功应用于推荐系统。文献［40］通过关系粒化思想提出了商网络的构造方法，从而大大减少了商网络的节点及其连边的规模，为探讨如何提高网络最大流计算效率提供了理论参考。总之，商空间理论是一种特色比较鲜明的多粒度数据分析方法，它在粒化论域的同时也对属性和结构进行粒化，某种程度上体现了特定的拓扑结构思想。

1.2 基于序贯三支决策的多粒度数据分析

序贯三支决策［16］是三支决策理论中用于处理多粒度数据的一种主要分析方法，它的核心思想如图2所示，也就是通过某种方式反复对论域U进行三分粒化（通常借助于0到1之间的2个阈值参数α，β（α<β）来完成，即满足约束条件大于等于β的对象分成一类，小于等于α的对象归为另一类，介于它们之间的对象又是一类），在此基础上讨论三分类问题，通常称这三个类分别为接受域、拒绝域和不承诺部分。实际上，不承诺意味着不确定、暂时不采取措施的意思，接受或拒绝则表明已明确其决策结果。一般地，为了解决具体的实际问题，对论域U进行反复粒化是一个不确定域（不承诺部分）逐渐减少的过程，因为序贯三支决策的目的并非不进行决策，而是通过暂时延缓决策以减少误判等行为而付出的额外代价［41⁃43］。众所周知，随着时间的推移，如果信息能够得到不断完善或补充，那么不确定域最终有望变成空集，此时三分类问题就退化为二分类问题，从而做出明确的误分类代价或测试代价较少的决策。当然，在最坏的情况下，很可能最终仍有一部分对象无法进行明确的决策，此时不得已只能随机将其划分到接受域或拒绝域［44］。需要指出的是，到底是何种原因导致人们对论域U进行反复粒化，这取决于拟解决问题的具体需求。据统计，使用序贯三支决策常见的情形大致可以分为：（1）属性的动态变化［45］，比如增加属性或减少属性；（2）属性值的粗化或细化［46］，即让属性取值个数增多或减少；（3）多粒度属性的跨粒度层组合［47⁃48］，换言之，属性取值之间拥有某种结构信息；（4）参数变化导致的论域多划分［49］，即参数在某一范围内任意取值使得划分的结果不断变化；（5）优化分类效果［43，50］，以逐步降低误分类代价；（6）一簇关系引起的论域多分类［51］，也是各种组合多粒度思想的具体体现［52］。目前，序贯三支决策已应用于多种多粒度数据分析任务中，比如分类［51］、聚类分析［44，53］、深度学习［54］、图像识别［55⁃56］、多属性决策［57］、推荐系统［58⁃59］、概念认知学习［60］和冲突分析［61］等。更多有关序贯三支决策的研究工作参见文献［62⁃63］，其中文献［62］给出了序贯三支决策的通用数学模型，归纳了形成序贯三支决策各种不同的组合情况，文献［63］则是通过复杂网络分析三支决策研究工作之间的关系，对了解序贯三支决策在三支决策理论中的具体贡献以及发展状况有一定的参考意义。

图2 序贯三支决策Fig.2 Sequential three⁃way decision

1.3 基于多粒度粗糙集的多粒度数据分析

实际上，乐观与悲观多粒度粗糙集是信息融合（多约束问题）的两种极端情况，即要么满足一个约束条件即可，要么所有的约束条件都必须满足。当然，推广到部分约束条件成立的多粒度粗糙集也不是难事，它是一种折中的信息融合模式，但是到底哪些项应处理成乐观约束条件而另外的当作悲观约束条件，则需要根据具体问题进行具体分析［64］。更一般地，约束条件的权重有时不一定相等，也就是研究代价敏感多粒度粗糙集也是有必要的［7］。此外，将上述模型中的属性子集替换成近似空间，可以得到通用的多粒度粗糙集模型，详见文献［65］。根据上述讨论，多粒度粗糙集的核心思想如图3所示，其中融合策略可根据具体问题的研究背景灵活选取。

图3 多粒度粗糙集的核心思想Fig.3 Key idea of multi⁃granulation rough set

目前，多粒度粗糙集已有众多的扩展模型，归纳起来主要有3种扩展方式：（1）将等价关系集R1，R2，…，Rk替换成其他各种二元关系［66⁃73］，定义广义多粒度粗糙集，增强模型适应环境的能力；（2）从单论域扩充到双论域，即各种类型的双论域多粒度粗糙集及其在多属性决策中的应用［74⁃77］；（3）与其他理论（如决策粗糙集、证据理论、三支决策和灰色系统）相结合，得到表达能力更强的多粒度粗糙集混合模型，比如多粒度决策粗糙集及各种推广［78⁃85］，证据理论下的多粒度粗糙集［86⁃87］，灰色多粒度粗糙集［88⁃89］等。在多粒度粗糙集研究领域中，比较常见的问题包括：多粒度粗糙集的粒度结构［90⁃91］，属性约简［92⁃93］，规则提取［94⁃95］，多源数据分析［96⁃97］以及动态环境下的知识更新［98⁃99］等。有关多粒度粗糙集的更多介绍参见文献［97，100］。总之，多粒度粗糙集是信息融合的一种有效方法，根据诱导信息的关系不同以及应用的差异已提出多种数学模型，它的特点是依据实际需要对各种粒度进行交叉融合运算，以解决多粒度数据分析问题。

1.4 基于多尺度数据分析模型的多粒度数据分析

Wu⁃Leung模型［5］是多尺度数据分析的原型方法，它的核心思想如图4所示，图中每个尺度下的数据对应着论域U的一次粒化结果，且这些粒化结果之间能够形成粒度粗细关系，即信息呈现出从粗粒度到细粒度或从细粒度到粗粒度的规律。多尺度数据可简单理解为包含多尺度属性的信息系统，因此简称为多尺度信息系统，通常记为二元组(U，C)，其中C={akj|j=1，2，…，m；k=1，2，…，s}，m为属性个数，s为尺度个数。也就是，每个对象在同一个属性下会有多个取值，实际上它是同一个值在不同粒度空间中的不同表现形式，本质上仍为一个取值。比如，考试成绩95分，它在百分制的粒度空间中是95分，在五级制（优、良、中、及格和不及格）中是优，在二级制（及格、不及格）中则是及格。Wu⁃Leung模型主要研究以下问题：（1）目标概念的近似随尺度变化的规律；（2）约简随尺度变化的情况；（3）规则提取以及随尺度变化的关系。需要指出的是，无论是目标概念的近似、知识的约简，还是从数据中获取的规则，都可归为知识的范畴。从这一角度而言，Wu⁃Leung模型讨论了知识随尺度变化的规律。值得一提的是，Wu⁃Leung模型中留下的4个公开问题，成为后续众多学者继续深入研究的对象，比如决策属性也为多尺度形式的情况［101］，集值Wu⁃Leung模型［102］以及覆盖Wu⁃Leung模型［103⁃104］等。

图4 Wu⁃Leung模型的核心思想Fig.4 Key idea of Wu⁃Leung model

继Wu⁃Leung模型之后，一个有意思的问题是，在满足给定要求的情况下如何选取合适的尺度？于是，Wu和Leung又提出了最优尺度选择问题［105］，以寻找知识随尺度变化过程中出现的一个临界理想状态。这是非常有意义的课题，例如协调性问题［106］，人们总是希望找到满足协调性要求但粒度尽可能粗的尺度，因为粒度粗的尺度通常意味着数据采集的成本较低。之后，一些学者又相继提出了各种各样的Wu⁃Leung扩展模型。比如，文献［107］对多尺度决策系统的规则提取做了研究，文献［108⁃109］从局部视角又讨论了完备和不完备多尺度决策系统的规则提取，文献［110⁃111］在不完备多尺度决策系统中分析了最优粒度选择和规则提取问题，文献［81，112⁃113］将多尺度信息系统和多尺度决策系统推广到直觉模糊环境中以定义优势粗糙集、双量化粗糙集和多粒度决策粗糙集，文献［114］通过属性粒度树给出了多尺度决策系统的广义约简。另一方面，文献［115⁃116］考虑了属性之间的尺度个数不相等的Wu⁃Leung扩展模型，这种情况下的多尺度数据称为广义多尺度信息系统或广义多尺度决策系统，在此基础上重新研究最优粒度选择等也是有必要的［117⁃120］。此外，将Wu⁃Leung模型与其他理论相结合也受到了一些学者的关注，比如基于代价敏感分析和信息熵的最优尺度选择问题［121⁃124］，多尺度数据的三支决策动态更新模型［47⁃48，125］，多尺度数据的概念分析方法［126⁃128］，以及基于多尺度数据的多属性决策［129］等。总之，Wu⁃Leung模型针对多尺度数据研究知识随尺度变化的规律以及知识在哪个尺度下进行分析最为合适等问题，截至目前已取得系列成果，具有广阔的应用前景和发展潜力。

1.5 基于多粒度形式概念分析的多粒度数据分析

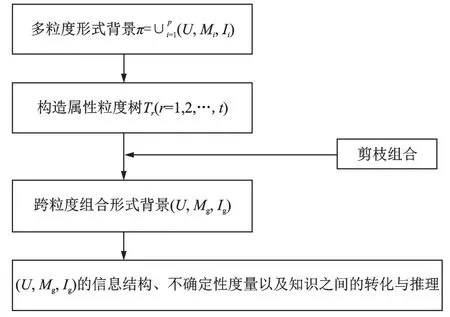
图5 多粒度形式概念分析的核心思想Fig.5 Key idea of multi⁃granularity formal concept analysis

实际上，这里的多粒度形式背景与多尺度信息系统是等价的，只是多粒度形式背景通过布尔属性来表示，而多尺度信息系统通过类别属性来刻画。换言之，多粒度形式背景可以通过多尺度信息系统进行转化得到，即将类别属性的每个取值看作一个布尔属性［20，126］。同理，多粒度形式背景也可以转化为多尺度信息系统，即将同类属性的布尔属性视作某一个类别属性的取值。除此之外，多粒度形式背景也可以认为是对形式背景的属性进行多粒度得到的［19］，但此时它的前提条件是原始的形式背景必须是可类属性块分割的［130］，因此从多尺度数据分析和形式背景的属性粒化两个角度出发研究多粒度形式概念分析不是等价的。

根据上述讨论可知，有2种研究多粒度形式概念分析的途径：（1）在形式背景的属性粒化的基础上讨论概念知识之间的转化关系［131⁃132］；（2）直接在多粒度形式背景的基础上对概念知识发现进行研究［126，133］。目前，基于多粒度形式概念分析的多粒度数据分析，主要集中在以下几个方面：（1）属性粒度树的剪枝方式以及数据跨粒度组合的合理性［134⁃135］；（2）对多粒度形式背景中的布尔属性进行扩展，比如推广到不完备数据集［136⁃137］等；（3）通过经典的概念格扩展模型，推广传统的多粒度形式概念分析方法，像面向对象和面向属性概念格［131⁃132，138⁃139］、区间概念格［140］等；（4）讨论多粒度形式背景的不确定性度量、类属性块以及属性粒度树的重要性、属性约简和最优粒度选择等［141］；（5）多粒度形式概念分析与其他多粒度数据分析方法之间的联系与区别。

最后需要指出的是，在机器学习领域中，也存在一些多粒度数据分析方法，其中多粒度学习就是基于粒计算而提出的有效方法之一，它的理论框架大致如图6所示，其中分类训练包括2大类：（1）标签结构信息的训练，也就是多粒度分类问题，即分类任务与粒度密切相关，有些样本在粗粒度中进行分类即可，不宜在细粒度中分类（容易出现误分类现象），而有些样本则需要具体到最细的粒度层面；（2）传统的分类训练，即训练一个单粒度分类器。一般地，多粒度学习的特点是通过对数据粒度进行不断调整，以得到研究对象比较满意的分类结果（有时还包括分类间的结构信息），以帮助分析数据和解决复杂问题［4，8，142］。以粒球计算方法为例，通过自适应调整粒球的中心和半径，得到粒球的训练结果再对标签进行预测。该方法的优势是将分类器的输入从单个样本提升到粒球级别（体现了经典的粒计算思想，具体表现为提升研究对象的粒度维度），从而获得高效、鲁棒和可扩展的分类器，详见文献［143⁃144］。实际上，在粒球计算方法提出之前，邻域粗糙集［22］已对数据进行多粒度分析研究，只是该模型受参数影响较大而已，但是后续的改进模型表明基于邻域粗糙集的多粒度数据分析方法的分类效果和性能较好［145⁃146］。

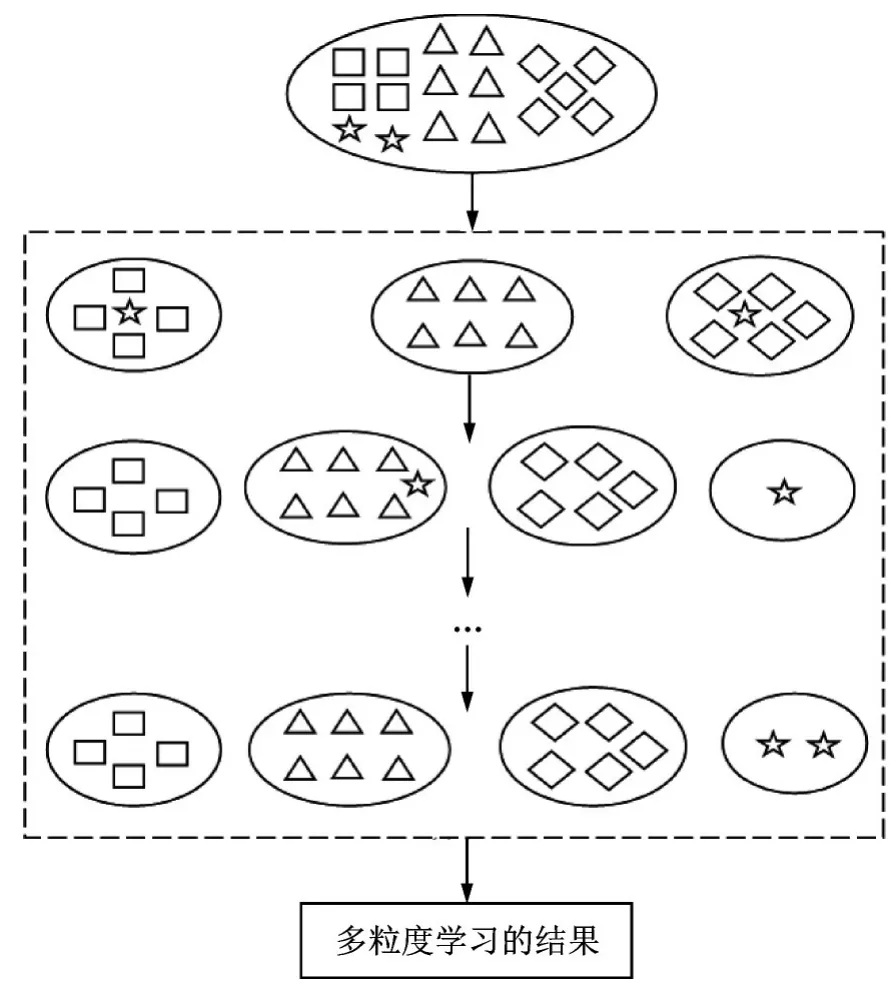
图6 多粒度学习的理论框架Fig.6 Theoretical framework of multi⁃granularity learn⁃ing

2 基于粒计算的多粒度数据分析的若干问题

本节对基于商空间理论、序贯三支决策、多粒度粗糙集、多尺度数据分析模型和多粒度形式概念分析等的多粒度数据分析研究中存在的问题进行归纳，便于今后对它们做进一步的讨论。

（1）基于商空间理论的多粒度数据分析。该方法的优势是提升解决问题的粒度维度，也就是将论域及其属性和结构进行多粒度，把研究对象从论域中的单个对象上升为对象聚成的类，与此同时也伴随着属性聚成的类和结构聚成的类，换言之，求解问题所涉及的研究对象的粒度变粗了。此外，保真和保假原理讨论了粗细粒度空间之间关于有解与无解的关系。这就引出一个问题：当保真和保假原理无法得出粗细粒度空间中有解和无解的有用关系时，如何能够事先判断商空间理论的适用性？因为多粒度思想不能发挥积极作用的情况偶尔也是存在的，比如当所要解决的问题对粒度不敏感时，如果事先可以得知商空间理论是否适用，那么将给使用者带来便利；另一个问题是在保真和保假原理能够有效发挥作用时，研究对象的粒度变粗是否通常都意味着计算效率的提高？这是一个非常有意思的问题，因为在其他领域中，一般都是以牺牲解的精度作为代价以提高问题求解的计算效率。因此，评估商空间理论的计算效率是一个重要的问题。

（2）基于序贯三支决策的多粒度数据分析。序贯三支决策通过信息或参数的不断更新形成论域的三分类序列，一般这些三分类序列能够形成粒度单调关系，也就是接受域和拒绝域不断变大，边界域（不承诺部分）逐渐变小，即它是延缓决策的一个有效过程。因此，一个很自然的问题是，如果存在误分类现象，那么所得到的三分类序列就未必是单调的，它是否会对严格要求决策过程遵循单调性的问题产生实质性的影响？因为有些问题希望基于单调的三分类序列进行决策分析，理由是它具有非常好的决策性质。换言之，不单调的三分类序列对实际中解决问题的影响到底有多大？或者存在扰动的序贯三支决策是否依然能够发挥出该方法的优势？这个问题一般要结合具体的应用场景进行分析较为合理，因为有些问题不注重序贯三支决策的过程而只关注问题求解的最终结果，还有一些问题则对序贯三支决策的过程要求比较严格，所以具体问题具体分析，但这方面有待深入研究。

（3）基于多粒度粗糙集的多粒度数据分析。该方法是通过多子集（多关系）融合以得到满意的目标对象近似结果，而且通常会合并粒度结构选择以及属性约简等问题一同进行研究。根据第1节综述的情况来看，经典的多粒度粗糙集模型已扩展到各种复杂的数据环境并与其他理论相结合进行推广研究和应用，取得了初步的成效。该方法的特点是利用信息融合（乐观与悲观信息融合）解决多粒度数据分析问题，其各种扩展模型亦是这个思路，但是今后该理论进一步发展可能会遇到的挑战性问题是：现有的多粒度粗糙集模型能否应用于具体的信息物理融合系统？因为信息物理融合系统是信息融合领域中的一个重要的研究对象，其应用前景非常广阔，也是信息融合方法具体落地的一个重要载体，若能够将多粒度粗糙集模型对应于某些具体的信息物理融合系统，做到理论联系实际，充分发挥出多粒度粗糙集模型的研究优势，服务于各种信息物理融合系统，那么这将是一个重大的突破，未来这方面的研究成果是可期的。

（4）基于多尺度数据分析模型的多粒度数据分析。多尺度数据分析方法的原型是Wu⁃Leung模型，此后的研究工作基本上都是针对Wu⁃Leung模型所做的各种推广及其具体应用。其中，比较经典的研究问题是最优粒度选择问题，它主要讨论如何在满足具体要求的情况下选择最粗的粒度，以降低解决问题所要付出的代价并寻找该问题在最粗粒度上进行解决的优点。一个比较有趣的问题是，现实中人们到底需要采集论域的多少个尺度才能比较满意地解决问题？因为数据采集的尺度越多，理论上就越有利于问题解决，但是数据采集的尺度越多通常意味着解决问题的成本越高，所以它是一个相互矛盾的问题，有必要针对特定的需求（像协调性问题、规则挖掘和知识发现等）开展进一步的研究，以获得平衡尺度个数（代价）和问题求解精度之间的关系。

（5）基于多粒度形式概念分析的多粒度数据分析。该方法利用类属性块、多粒度类属性块、剪枝形式背景以及多粒度剪枝形式背景等手段实现跨粒度层的概念知识表示与获取。根据第1节的综述情况来看，它主要集中在粗细粒度空间变化时概念知识如何进行相互转化以及怎样寻找到合适的粒度组合等问题。然而，计算复杂性一直是经典的形式概念分析在发展过程中遇到的一个瓶颈问题。因此，多粒度形式概念分析首要回答的问题仍然是能否显著提高概念知识及其运算的计算效率；如果可以，那么它将给经典的形式概念分析研究带来解决瓶颈问题的机遇。根据现有的研究经验，讨论粒概念子空间及其随粒度空间变化进行转化的规律是提高计算效率的一种有效方法，并且粒概念子空间可进一步应用于分类学习等问题。然而，粒概念子空间的选取通常与问题的研究背景密切相关，它的有效性在理论上进行严格证明存在一定的困难，因此需要提出一些选取粒概念子空间的有效方法。

（6）其他基于粒计算的多粒度数据分析方法。与第1节相对应，这里主要讨论多粒度学习研究中存在的不足。这类问题通常与机器学习相结合，依据讨论问题的不同可区分为2类：一类是利用近邻思想实现聚类，即通过对参数的调整使得聚类不断更新以获得满意的结果，因此选取合适的参数是该研究领域中的一个有价值的问题；另一类是识别样本的多粒度分类结构，有助于后续的样本分类预测，它们通常都在损失函数的指导下进行优化迭代或学习。然而，对于前者其参数优化是一个比较棘手的问题，目前大量的实验都是直接设定或根据经验巧妙设计参数，这种做法比较普遍，尤其是一个新提出的多粒度学习方法，往往在实验中人为直接设定参数；对于后者则需要预先判断样本是否存在多粒度分类结构，这需要一定的先验知识，但这样的先验知识不容易获取。因此，针对现有的各种多粒度学习方法，有必要提出更多、更好的自适应参数优化方法以及探测数据具有多粒度分类结构的有效手段，使得多粒度学习结果更具有说服力。

除了以上每一类多粒度数据分析方法自身存在的问题之外，在交叉融合研究中还存在一些挑战性的问题，下面逐一举例说明。比如，模糊商空间与聚类分析相结合可以得到聚类与商空间以及模糊相容或相似关系之间的联系［28，32，34］，但是聚类效果需要进一步评估；序贯三支决策用于图像处理时，在分类器训练阶段综合考虑了各种代价［54，56］，使得训练阶段可以适时停止，以优化训练阶段所付出的各种代价，但是训练阶段依赖于序贯粒特征学习，因此进一步讨论序贯粒特征对分类结果的具体影响是一个重要的问题；多粒度粗糙集在融合粒度知识时要求知识空间的层次是无差别的［17⁃18］，即能够对知识进行直接融合，但是有些粒度知识之间存在着明显的层次关系，不允许知识进行直接融合，它需要实施跨粒度层知识转化之后才能在同一个粒度层进行知识融合，所以如何进行知识跨粒度层转化以及确定合适的融合层是一个有意思的问题；在Wu⁃Leung模型与多属性群决策相结合时，利用专家打分构造多尺度属性之后再对各个单尺度数据进行信息融合产生总的信息表以解决决策不一致的问题［129］，那么如何融合各个单尺度数据才能使得最终得到的信息表可以做出较为合理的决策是一个有价值的问题；在多粒度形式概念分析与认知计算相结合时，如何建立多粒度概念认知学习的公理化框架、提出多粒度概念认知系统并实现多粒度概念认知过程都是非常有意义的研究课题。需要指出的是，这些问题仅仅只是基于粒计算的多粒度数据分析方法目前在交叉融合研究中存在的问题，随着交叉融合研究的深入还会有各种各样的问题不断涌现，甚至新的问题会覆盖或包含原有的问题，所以上述凝练得到的问题只有相对意义，或者说它们更多的则是起到抛砖引玉的作用。

3 结束语

本文对基于商空间理论、序贯三支决策、多粒度粗糙集、多尺度数据分析模型和多粒度形式概念分析等的多粒度数据分析研究工作进行了综述，指出了每一类多粒度数据分析方法的核心思想、基本问题以及主要研究思想，并提出了若干具有挑战性的问题，为今后进一步研究这些方法提供了理论参考。实际上，人们可以根据实际需要，基于粒计算思想提出各种各样的多粒度数据分析方法，但是这些方法的出发点是不同的，具体见第1节对每一类方法的详细介绍。但是，一个有意思的现象是，这些方法在研究过程中遇到的核心问题和得到的关键结论存在一定的相似性。比如，到底怎样才能高效地选取合适的粒度空间或粒度组合以得到满意的求解结果？它几乎是每种多粒度数据分析方法都会遇到的关键问题；此外，大部分的多粒度数据分析方法在研究过程中都会发现计算效率和求解结果与最终选取的粒度空间的粒度粗细程度密切相关。尽管如此，不同的多粒度数据分析方法会根据自身的优势采取不同的策略去解决这些问题，甚至有时候需要融合多种多粒度数据分析方法才能获得比较满意的结果，所以交叉融合研究是一种趋势，也是解决具体问题的一种必然。需要指出的是，数据驱动和问题驱动是该领域中比较常见的两种研究模式，即多粒度数据分析方法侧重于服务实际中的具体需求。除了本文介绍的多粒度数据分析方法之外，基于粒计算的类似研究还有很多，因此本文只是对该研究领域做了一个大致的综述，并未窥其全貌，也没有将该问题的所有重要工作都归纳总结到位，只希望起到一个抛砖引玉的作用。最后，相信今后会涌现出更多、更好的多粒度数据分析方法，进一步促进该研究领域的快速发展，这方面取得的研究成果将成为粒计算在数据分析应用中的标志性工作。