基于SPWVD和改进AlexNet的复合干扰识别

尚东东，张劲东，杜 盈，尹明月

（南京航空航天大学电子信息工程学院，南京211100）

引 言

随着雷达抗干扰技术的不断成熟和发展，单一形式的有源干扰很难对雷达形成预期的效果。复合有源干扰通过多种干扰信号的组合，例如压制干扰和欺骗干扰的组合，能够实现对雷达的多重特性干扰，使雷达无法判断其干扰环境，从而使抗干扰手段失去其有效性。复合干扰现在已成为雷达面临的主要挑战。作为抗干扰手段运用的提前和必须环节，复合干扰识别的研究具有重要理论意义和实用价值。

目前，国内外在有源干扰特征提取及识别方面开展了较多研究工作，但复合干扰识别的资料则相对有限。从现有工作看，欺骗干扰和复合干扰识别大多建立在信号变换域（时频域、双谱域、小波域和分形维数域等）进行特征提取，获得区分度明显的特征。文献［1］通过对雷达接收信号进行时频分析，比较了3种欺骗干扰时频图的差异性，提取时频图像特征进行有源欺骗干扰识别，但是该方法是基于决策树的识别，需要确定阈值；文献［2］通过提取欺骗干扰的双谱切片作为特征参数，输入支持向量机（Support vector machine，SVM）中进行识别，但SVM的核函数和一些常数没有理论证明；文献［3‑4］在时域、频域和分形维数域等提取复合干扰信号特征参数，输入神经网络分类器进行识别，但神经网络权值太多，计算量太大；文献［5］针对射频噪声同距离欺骗干扰的复合干扰信号，采用提取盒维数和L‑Z复杂度分布特征的方法，对复合干扰信号实现了分类识别，但其对所选参数敏感，无法区分更多类型的复合干扰。因此由于复合特征提取和识别算法参数难度大，目前针对多种复合干扰的识别并无有效算法支撑。

随着机器学习理论的深入发展，深度学习方法开始应用于干扰识别等领域。深度学习中的自编码器［6］、卷积神经网络［7］与机器学习模型相比，其模型泛化能力更强，更能刻画数据的特征，分类效果更好。AlexNet比LeNet5多出了非线性激活函数、随机稀疏和局部响应归一化等模块，对图像能够自动提取更多区分度和稳定性高的特征［8‑9］，而且Alex Net模型参数远小于VGGNet等更深层卷积神经网络的模型［10］，所以从训练的时间复杂度和提取特征的稳定性考虑，AlexNet网络更适用于雷达信号识别。

针对上述问题，本文提出了一种基于伪平滑魏格纳‑威利分布（Smoothed pseudo Wigner‑Ville distri‑bution，SPWVD）和改进AlexNet的复合干扰识别方法。该方法通过SPWVD进行时频分析，提取复合干扰时频图像，在时频特征进行降维的基础上，结合改进的Alex Net模型，采用多个小的卷积核替代大的卷积核，删除全连接层7和局部响应归一化模块等手段，减小网络参数从而加快计算速度，实现雷达复合干扰信号的分类识别。

1 复合干扰信号的时频分析

1.1 复合干扰信号模型

作为有源干扰的种类之一，压制干扰信号是用高斯白噪声对高频载波进行调制干扰［11］。从形成方式对噪声干扰进行分类，主要有噪声调幅（Noise amplitude modulation，Noise AM）干扰和噪声调频（Noise frequency modulation，Noise FM）干扰等。噪声调幅干扰和噪声调频干扰均可在载频附近形成强噪声分布，而噪声功率分布的范围取决于调制噪声的带宽。

欺骗干扰以近似雷达回波的信号影响雷达目标信号检测，也是有源干扰的种类之一。拖引干扰是欺骗干扰的主要形式，主要包括距离波门拖引干扰（Range gate pull off，RGPO）、速度波门拖引干扰（Velocity gate pull off，VGPO）、距离‑速度联合波门拖引干扰（Range‑velocity synchronous gate pull off，R‑VGPO）。

本文针对的复合干扰模型是压制干扰与欺骗干扰的复合。根据以上分析，形式包括距离波门拖引复合噪声调幅信号、距离波门拖引复合噪声调频信号、速度波门拖引复合噪声调幅信号、速度波门拖引复合噪声调频信号、距离‑速度联合拖引复合噪声调幅信号、距离‑速度联合拖引复合噪声调频信号。

信号的复合方式有3种，分别是加性复合、乘积复合和卷积复合［4］，其中加性复合的干扰效果较好［11］，本文仅讨论加性复合。

1.2 基于SPWVD的复合干扰特征提取

时频分析方法是常用的提取时变非平稳信号特征的方法，其中魏格纳-威利分布（Wigner‑Ville distribution，WVD）是一种具有多种优良性质的二次变换［12］。对于复合干扰信号s(t)，其WVD分布定义为

式中SPWs1s2(t，f)和SPWs2s1(t，f)是s1(t)和s2(t)的互SPWVD。因为窗函数h(τ)和g(u)在时间、频率方向进行平滑，因此SPWVD产生的交叉项影响要远小于WVD。

图1（a）所示为两个信号相加的WVD分布，从图中可以看出有明显的交叉项。本文讨论的复合干扰指的是波门拖引信号同调制噪声的线性复合，而针对波门拖引信号的识别往往在拖引期，即同一时间雷达会收到真实回波和假目标回波，WVD会影响雷达复合干扰信号的识别。图1（b）所示为SP‑WVD图，从图中可以直观地看出，相比于WVD，SPWVD变换明显降低了两个信号的交叉项。因此，本文使用SPWVD变换获得复合干扰信号的时频图像。图2显示了在干（信）噪比为0 dB下目标信号和复合干扰信号的SPWVD时频图。从图2可以发现，7种时频图特征差异明显，因此通过SPWVD分布图来实现复合干扰信号的识别成为可能。

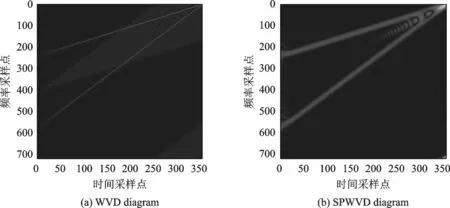
图1 两个信号叠加的时频图Fig.1 Time-frequency diagram of two superimposed signals

图2 目标信号和复合干扰信号的SPWVD时频图Fig.2 SPWVD time-frequency diagrams of target signal and composite jamming signal

1.3 基于离散化SPWVD的复合干扰特征降维

由于复合干扰的SPWVD特征集中在某一斜线区域，且该区域的斜率与线性调频信号的斜率有关，因此，该区域位置大小可以提前预知。此外，为了减小SPWVD的计算量，可以将式（4）的SPWVD形式进行离散化，通过对预定区域的离散化直接获得复合干扰特征，从而形成降维。

离散化SPWVD变换获得复合干扰信号的时频图像可以按照以下方法。令t=nTs（Ts为采样周期），f=m/N（N为一个周期内的采样点数），则式（3）可变为

式中：L1（假定为奇数）是g(n)的窗长度，L2（假定为奇数）是h(m)的窗长度，0≤n≤N、0≤m≤N、-(L1-1)/2≤l≤(L1-1)/2和-(L2-1)/2≤i≤(L2-1)/2为分别对应于连续变量t、f、u和τ的离散变量。

预定区域的获取可以采用图像裁剪的方法。设线性调频信号的斜率为k，斜线区域上下两侧的点为(n0，m0)和(n1，m1)，则预定区域为

式中：A和Ar分别为裁剪前后的图像矩阵，1≤j≤N。

最后利用最大值最小法进行归一化处理裁剪后的图像，进一步减小数据量。图3为复合干扰特征降维流程图。

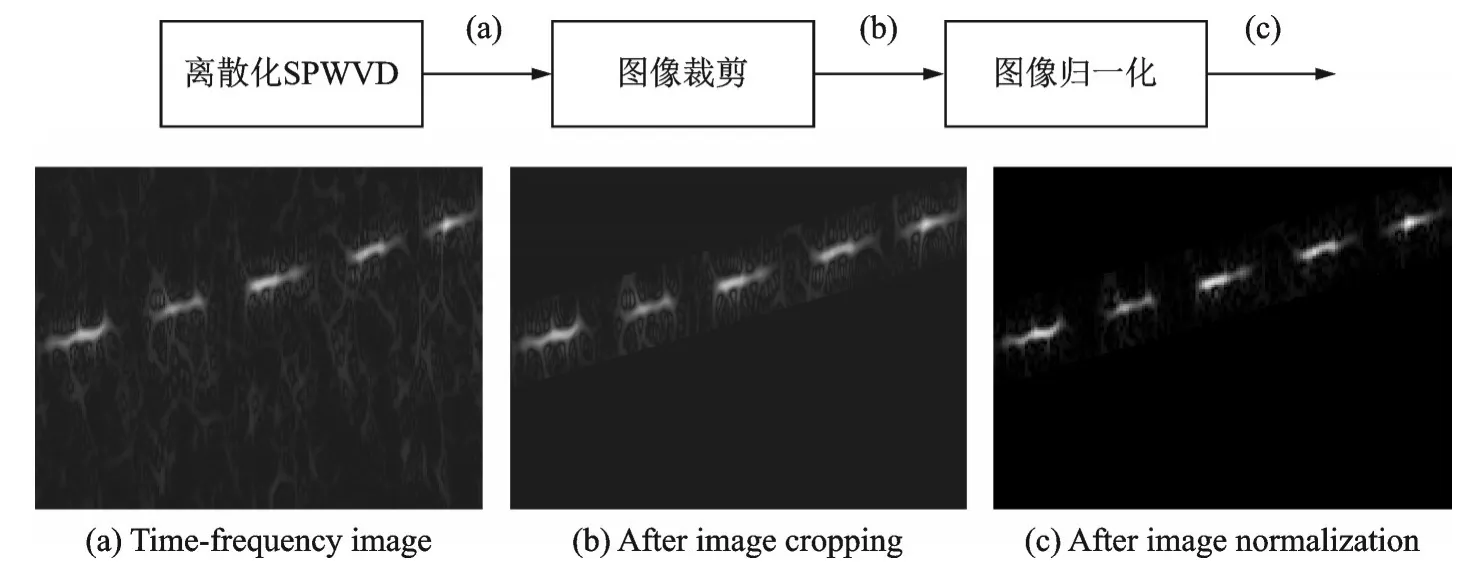
图3 复合干扰特征降维流程图Fig.3 Flow chart of composite jamming feature dimensionality reduction

2 卷积神经网络设计

2.1 Alex Net模型结构

AlexNet是在LeNet5基础上进一步发展和改进的深度卷积神经网络［13］，相比于LeNet5，它具有局部区域感知、权值共享的特点。图4所示的Alex Net网络结构共分为11层，其中前5层为卷积层，中间3层为池化层，后3层为全连接层。卷积层与池化层相互交叉堆叠，整个网络可视为8层。卷积层后面分别采用了如式（7）的线性整流函数、如式（8）所示的局部响应归一化（Local response normalization，LRN）等模块。将卷积层与池化层相互交叉叠加，然后连接全连接层，通过反向传播算法训练卷积核权重参数，可得到AlexNet网络。

2.2 AlexNet模型的改进

本文采用的网络结构如图5所示。相比于AlexNet网络，本文网络进行了以下的改进：

（1）卷积层1用7×7和3×3的3个小卷积核代替原来11×11的大卷积核，卷积层2用两个3×3的卷积核代替原来5×5的卷积核，具体参数如表1所示。采用较小的卷积核可以提取更加深层次的图像特征。两个3×3的堆叠卷积层不仅感受野是5×5，而且比一个5×5卷积层有更多的非线性，使得判决函数更有判决性，并起到隐式正则化的作用。

图4 Alex Net网络结构Fig.4 Structure of AlexNet network

图5 改进的Alex Net网络结构Fig.5 Structure of the improved AlexNet network

表1 Conv 1和Conv 2的具体参数Table 1 Specific parameters of Conv 1 and Conv 2

（2）删除LRN模块。在设置LRN层参数时往往需要通过交叉验证得到，并且如果通过适当的参数初始化和归一化操作之后，LRN层不能提升网络的泛化能力。因此，删除LRN层会使得本文的模型更易并行化。

（3）删除原模型的全连层7。全连接层参数占AlexNet网络总参数的96.2%，删除一个全连接层，可减少网络参数，加快网络的计算速度。

相比于AlexNet，本文网络更深更瘦，高瘦的网络要好于矮胖的网络，改进的模型参数如表2所示。图6为本文提出的基于SPWVD和改进Alex Net的复合干扰识别算法流程。

表2 本文网络和原网络参数对比Table 2 Comparison of network parameters inthis article and the original network

图6 识别算法流程Fig.6 Flow chart of recognition algorithm

表3 实验参数Table 3 Experimental parameters

3 仿真分析

仿真参数设置如表3所示。按照表中的复合干扰模型在干（信）噪比0到15 d B之间产生7种雷达接收信号各1 000个，每个dB的总训练集是7 000个，每个雷达接收信号另随机产生250个样本，总测试集是1 750个。

图7和图8分别为在干（信）噪比为3 dB下AlexNet网络和本文网络的训练集和测试集的损失及准确率变化曲线。从图中可以看出，本文网络在很多时候都比AlexNet网络损失值低，且下降的速度更快，识别率更高。这正是由于采用小的卷积核代替大的卷积核，提取了更加深层、细致的图像特征，删除一个全连接层，减小网络的参数，从而加快了计算速度。

图9为采用本文网络测试集识别率随干（信）噪比变化的统计结果，从图中可以看出，随着干（信）噪比的提高，7种信号的识别性能得到提升，在干（信）噪比为0 d B时，每种信号的识别率均在90%以上。

图10为Alex Net网络和本文网络整体识别率的对比。从图中可以看出在干（信）噪比为0 dB时，AlexNet网络和本文网络的整体识别率分别为92.4%和93.7%；在干（信）噪比为5 dB时，AlexNet网络的识别率为98.4%，本文网络识别率为98.8%。本文网络的识别率明显高于AlexNet网络。

图11为干（信）噪比为6 dB下使用本文网络生成的识别混淆矩阵，其中3个距离拖引复合噪声调幅信号错误识别为距离‑速度联合拖引复合噪声调幅信号，1个距离拖引复合噪声调频信号错误识别为距离‑速度联合拖引复合噪声调频信号，4个距离‑速度联合拖引复合噪声调幅信号错误识别为距离拖引复合噪声调幅信号两个距离‑速度联合拖引复合噪声调频信号错误识别为距离拖引复合噪声调频信号，整体识别率为99.2%。

为了探究复合干扰中波门拖引信号与噪声调制信号的功率比对识别性能的影响，在干（信）噪比为3 d B的条件下进行仿真，图12为识别率随波门拖引信号与噪声调制信号功率比的变化曲线图。从图中可以看出功率比在-5∼6 dB时，识别率均在90%以上，说明本文算法良好的稳定性。

为了验证本文算法的有效性，将本文算法与文献［4］中的4种方法比较，图13给出了5种算法识别率比较结果。从图13可以看出，在干（信）噪比大于0 d B时，本文算法的识别效果较其余4种算法有较大提升。

图7 训练集损失及准确率随迭代次数变化曲线Fig.7 Change curve of training set loss and accuracy rate versus the iteration number

图8 测试集准确率随迭代次数变化曲线Fig.8 Change curve of test set accuracy versus the iteration number

图9 复合干扰信号识别率曲线Fig.9 Composite jamming signal recognition rate curve

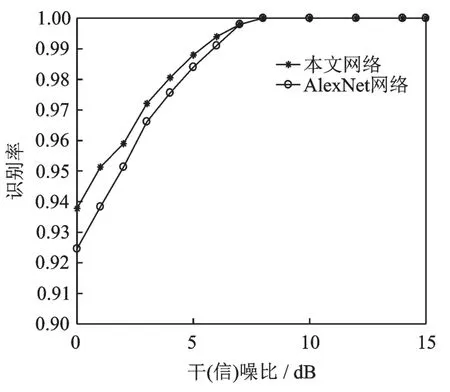
图10 AlexNet网络和本文网络识别率比较Fig.10 Recognition rate comparison between Alex Net network and this article network

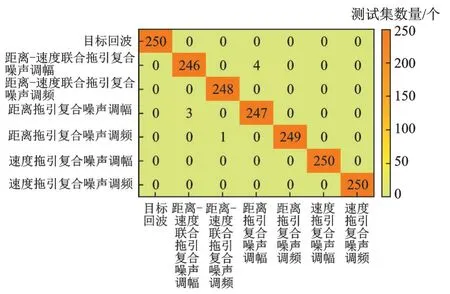
图11 干(信)噪比为6 dB的混淆矩阵Fig.11 Confusion matrix with jamming(signal)to noise ratio of 6 dB

图12 识别率随波门拖引信号与噪声调制信号功率比的变化曲线Fig.12 Change curve of recognition rate versus the power ratio of gate pull off signal to noise modulation signal

图13 5种算法识别率比较Fig.13 Recognition rate comparison of five algorithms

4 结束语

针对复合干扰识别难度大的问题，本文提出了一种基于SPWVD和改进Alex Net的复合干扰识别算法。该算法对复合干扰信号进行时频分析，对时频特征进行降维，最后结合改进的Alex Net模型，使用小的卷积核，删除全连接层7和局部响应归一化模块等手段，完成复合干扰的识别。仿真结果表明，改进后的AlexNet网络在识别准确率方面较AlexNet模型有较明显的改善，在干（信）噪比为0 dB时，目标信号和6种复合干扰信号的识别率均在90%以上。下一步的研究重点就是寻找更高效率的深度学习模型。