球阀固-液两相流流动特性与压力损失数值模拟

2021-06-21石喜贡力陶虎李露李江涛

中南大学学报（自然科学版） 2021年5期

石喜，贡力，陶虎，李露，李江涛

(兰州交通大学土木工程学院，甘肃兰州，730070)

含沙水流的水力输送广泛存在于水利、环保和市政等领域。在水力输送管道中，球阀作为重要的水力元件常常用于控制流量、调节压力。含沙水流在球阀中运动时，受阀芯结构的影响，其流场特性和压力损失要比单相流复杂得多，还有可能使球阀产生冲蚀磨损，影响球阀的运行安全，因此，有必要对球阀的固-液两相流特性进行探讨。人们采用试验和数值模拟方法对各类阀门两相流的特性如气-固两相流的流动特性[1]、冲蚀特性[2]，气-液两相流的流场特性[3]、流量系数[4]、压力降[5]等进行了研究。在阀门固-液两相流方面，WHEELER 等[6]研究了含沙水流对节流阀的冲蚀特性，发现在节流阀中加入CVD 金刚石涂层可提高阀门的抗冲蚀性能；HU等[7]采用DPM模型研究了节流阀中固-液两相流的抗冲蚀磨损特性；訚耀保等[8]采用CFD与冲蚀模型对射流管伺服阀多相流中固体颗粒物和油液的运动及冲蚀磨损进行了数值模拟研究；马艺等[9]利用雷诺应力模型和欧拉-欧拉方法对球阀的开启压差及压力分布特性进行了研究；杨国来等[10]采用数值模拟对某黑水调节阀在2种开度下的阀门流场进行了分析；余天赐[11]对球阀固-液两相流的流动及磨损特性进行了研究；崔之健等[12]对除砂器中携砂液流对针型阀的冲蚀特性进行了数值模拟。可以看出，前人对各类阀门的两相流研究以气-液两相流压力损失变化规律的研究为主，而对球阀固-液两相流压力损失变化规律的研究较少。为此，本文作者以常见的PVC 球阀为研究对象，采用Eulerian双流体模型进行数值模拟，得到不同阀门开度时流场变化、颗粒分布特征，以及流速、开度、颗粒体积分数和颗粒粒径的变化对球阀压力损失的影响规律，以期为水力输送管道的设计提供参考。

1 数学模型

1.1 两相流数学模型

选用Eulerian 模型进行球阀固-液两相流数值模拟。Eulerian模型属于欧拉-欧拉连续流体模型，将颗粒相作为拟流体，认为颗粒相与流体相是共同存在的连续介质，两相都在欧拉坐标系下计算[13]。基于Eulerian 模型建立的固-液两相流基本方程包括连续性方程和动量方程[14]。

液相和固相的连续性方程分别为：

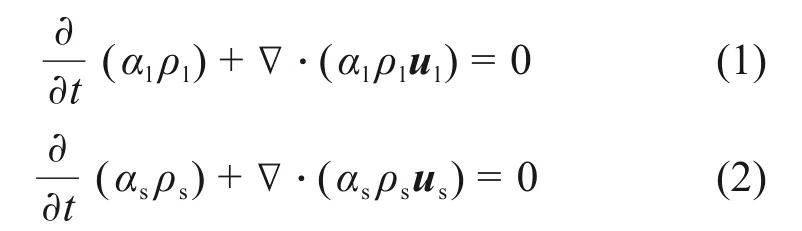
式中：ρl和ρs分别为液相密度和固相密度；αl和αs分别为液相体积分数和固相体积分数，αl+αs=1；ul和us分别为液相速度和固相速度；∇为拉普拉斯算子；t为时间。

液相和固相的动量方程分别为：

式中：p为静压；ps为固相压力；g为重力加速度；和分别为液相和固相的应力-应变张量；Mi为两相间的体积作用力。

考虑相间作用，由于颗粒密度大于水流密度，因此，可将颗粒所有的虚质量力忽略[15]。在数值计算时考虑拖曳力和升力的影响，动量传递方程如下[16]：

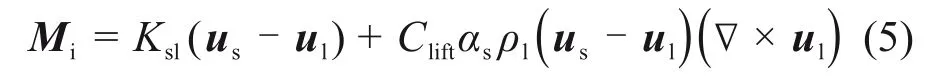
式中：Ksl为相间动量交换系数；Clift为升力系数，本文计算时取0.5。

1.2 湍流模型

采用混合标准k-ε湍流模型进行数值计算。混合标准k-ε湍流模型是单相湍流模型的一种扩展，在计算时考虑两相之间的相互作用，其k方程和ε方程分别如下[16]：

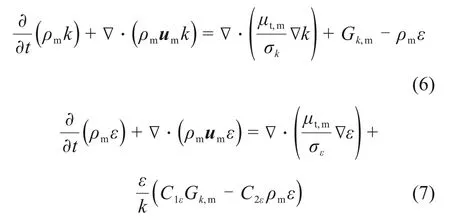
式中：μt,m为混合相湍流黏性系数；σk和σε分别为与湍动能k和耗散率ε对应的Prandtl数，分别取1.0和1.3；ρm为混合相密度；Gk,m为湍流动能产生项；um为混合相速度；C1ε和C2ε为经验常数，分别取1.44和1.92。

2 几何模型与计算方法

2.1 几何模型

PVC 球阀的结构如图1所示，由手柄、阀杆、阀体和球体等组成，其启闭件是1 个有孔的球体，与阀杆和手柄连接，通过手柄旋转绕垂直轴线的启闭件来启闭通道。

图1 PVC球阀结构示意图Fig.1 Structure sketch of PVC ball valve

本文数值计算采用的球阀为DN75PVC 球阀，球体通道内径为57.8 mm。图2所示是球阀开度为50°的几何模型，其中，上游和下游连接管道为DN75 的PVC 管道，内径为67.8 mm，管道水平放置。计算模型的几何区域取上游长度L1=1 025 mm(L1＞10d，d为管道的公称外径)，下游长度L2=1 400 mm(L2＞15d)。为了保证计算流动的稳定性，取压点分别设置在上游10d和下游15d的位置处。计算时，液相为水(温度为20 ℃)，固相为泥沙颗粒，密度为2 650 kg/m3。相间的拖曳力选用Syamlal-O′brien模型，考虑重力的影响，重力方向取Z轴的负方向。

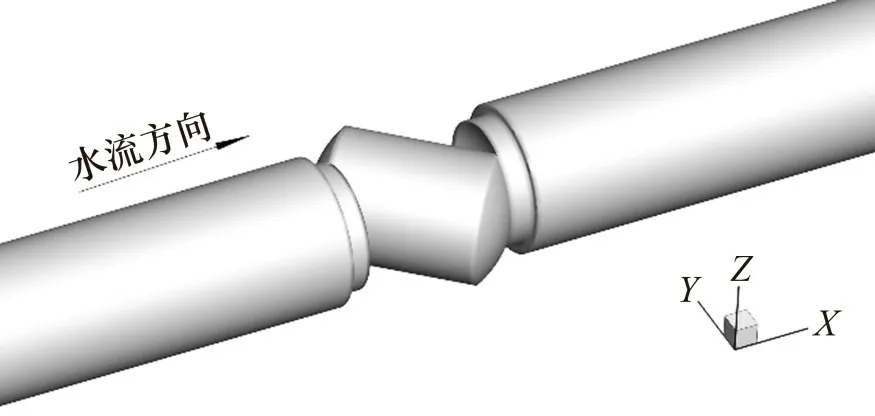
图2 几何模型Fig.2 Geometric model

2.2 网格划分及网格无关性检验

采用Gambit 软件对计算区域进行网格划分。在球阀阀芯位置采用非结构网格，其余部位采用六面体结构网格。为了保证网格数量对计算结果的影响较小，需进行网格无关性检验。以进口速度为3 m/s、球阀开度为70°、颗粒体积分数为10%、粒径为0.08 mm 时的球阀压力损失Δpb为指标进行网格无关性检验，结果如图3所示。从图3可以看出：当计算区域的网格数量大于45万个时，可保证计算结果的精度。在不同开度时，本文取计算区域的网格数量为47.2 万～48.4 万个。图4所示为网格划分图(球阀开度为50°)。

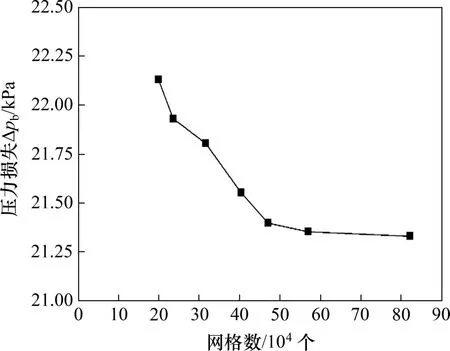
图3 网格无关性检验Fig.3 Mesh independence test

图4 网格划分Fig.4 Mesh generation

2.3 离散格式与边界条件

采用相间耦合的SIMPLE 算法进行迭代求解，对近壁区流动采用标准壁面函数法进行计算。边界条件进口采用速度进口条件，连续相运动速度与颗粒相运动速度相同；出口采用自由出流边界，所有方程迭代残差收敛标准设为10-4。

2.4 计算模型验证

由于球阀固-液两相流方面的试验数据较少，本文采用GILLIES等[17]在水平直管段中的水沙两相流试验结果进行验证。由于直管段与球阀中水流运动规律以及产生压力损失的机理相同，而且球阀在开度较大时的流动特性与水平直管的流动特性相似，因此，经过验证后的计算模型可用于球阀固-液两相流计算。GILLIES 等[17]的试验参数如下：管道长度为10 m，内径为103 mm，泥沙颗粒密度为2 650 kg/m3，颗粒粒径为0.09 mm，颗粒的体积分数分别为19%和29%，管壁的粗糙度为2 μm。图5所示为单位长度压力损失Δpb的计算结果与试验结果。从图5可以看出：在不同颗粒体积分数和速度时，单位长度压力损失计算结果略大于试验结果，但整体上保持较好的一致性且基本接近，表明Eulerian 模型能够较好地模拟固-液两相流动。

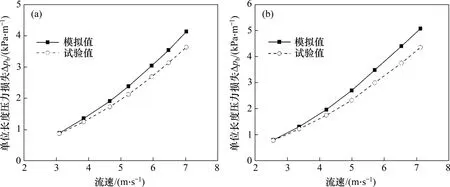
图5 压力损失数值模拟结果与试验结果对比Fig.5 Pressure loss comparison of numerical simulation results with experimental results

3 结果与分析

3.1 混合相流场分布

当进口流速为2 m/s，颗粒体积分数为10%，粒径为0.08 mm 时，不同开度的XY截面混合流速分布和流线如图6所示。由图6可以看出：当球阀开度为90°时，混合流速分布和流线较均匀，由于阀芯通道的直径小于管道直径，导致通道内出现流速梯度，中间速度较大，阀芯出口管壁处出现局部低速区；随着球阀开度减小，阀芯通道进口混合流面积不断减小，在通道内形成较大的流速梯度，中间部位流速较大，而流速梯度随着开度减小而增大。从流线变化可以看出：当球阀开度为90°时，流线平顺；当球阀开度为70°和50°时，由于球阀呈半开状态，混合流进入阀芯后在上侧形成漩涡；而当球阀开度为40°时，阀芯上侧仍有漩涡。从阀后流线变化看，球阀开度小于70°时发生回流，回流尺度随开度减小而增大，这是阀后过流面积减小所致。可以看出，球阀开度对混合流流场分布的影响较大。

图6 混合流速度分布及流线Fig.6 Velocity distribution and streamlines of mixed flow

3.2 颗粒体积分数分布

当进口流速为2 m/s、颗粒体积分数为10%、粒径为0.08 mm时，不同开度XZ和YZ截面颗粒体积分数度分布以及YZ截面上Z方向的涡量如图7所示。通过涡量可分析颗粒体积分数的变化情况。从图7可以看出：在进口S1 截面，由于重力的影响使颗粒在上部颗粒体积分数较低，下部颗粒体积分数较高，不同开度时S1 截面的颗粒体积分数分布相似；涡量的变化与颗粒体积分数变化相反，在涡量大的区域颗粒体积分数较低，而在涡量小的区域颗粒体积分数较高，这是由于S1 截面整体流动的湍动能较小，此时涡量的变化对颗粒体积分数分布影响较大，涡量大的地方湍动剧烈使颗粒分散。

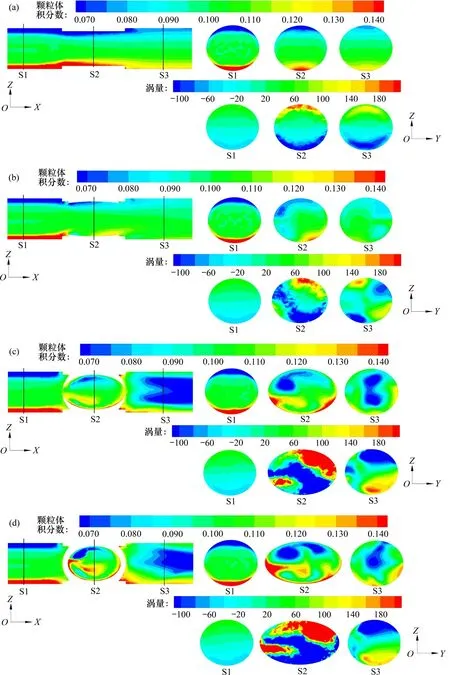
图7 开度不同时颗粒体积分数分布与涡量分布Fig.7 Distribution of particle volume fraction and vorticity at different openings

在阀芯S2 截面，当开度为90°和70°时，颗粒体积分数梯度较小；整体流动的湍动能较小，颗粒分布受涡量变化影响，表现为涡量大的区域颗粒体积分数较低，而涡量小的区域颗粒体积分数较高；在开度为50°和40°时，颗粒体积分数梯度较大，并且分布较乱，出现的颗粒低体积分数区域和高体积分数区域较多，此时涡量的变化也较乱。这是由于在开度为50°和40°时，阀芯内的紊动加大，加速了颗粒与水流的运动，而流通面积的减小使回流区域增多，使得颗粒在部分区域堆积形成高体积分数区，在部分区域冲散形成低体积分数区。这说明在流动紊动剧烈时，颗粒分布不受涡量的影响。

在出口S3 截面，当开度为90°和70°时，颗粒体积分数分布相似；当开度为50°时，中间部位颗粒体积分数较低，出现2个低体积分数区域；而当开度为40°时，中间体积分数低，分布相对均匀。从涡量变化来看，当开度为90°时，流动湍动能较小，颗粒体积分数分布受涡量变化的影响较大；而在其分开度时，由于受阀芯扰动的影响，S3 截面的颗粒体积分数分布不受涡量影响。

3.3 压力损失变化

3.3.1 球阀压力损失计算

固-液两相流经过球阀时的压力损失可表示为

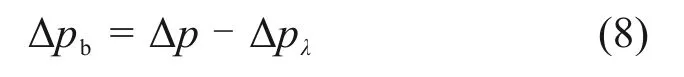
式中：Δpb为混合流经过球阀的压力损失；Δp为球阀上下游2 个取压点之间总压力损失；Δpλ为相应直管段混合流的摩阻损失。

通过对相应直管段计算可得到相应工况下混合流的水力坡度im，摩阻损失Δpλ可采用下式计算：

式中：im为相同工况下混合流的水力坡度；ΔL为直管段长度。

3.3.2 球阀压力损失随阀门进口流速的变化

当颗粒粒径为0.08 mm、颗粒体积分数为10%和20%时，球阀两相流压力损失Δpb随进口流速的变化如图8所示。从图8可见：在不同开度时，球阀压力损失随流速增大而增大。这是由于随着流速增大，两相流经过球阀时加剧了水流的紊动程度，水流的剧烈紊动加速了颗粒的运动，使得液相损失和固相损失[18]均增大，因而压力损失增大。从图8还可看出：当开度为90°和70°时，压力损失的变化幅度较小，而在开度为50°时，压力损失的变化幅度较大，这说明当开度较小时，流速对压力损失的影响更加明显。

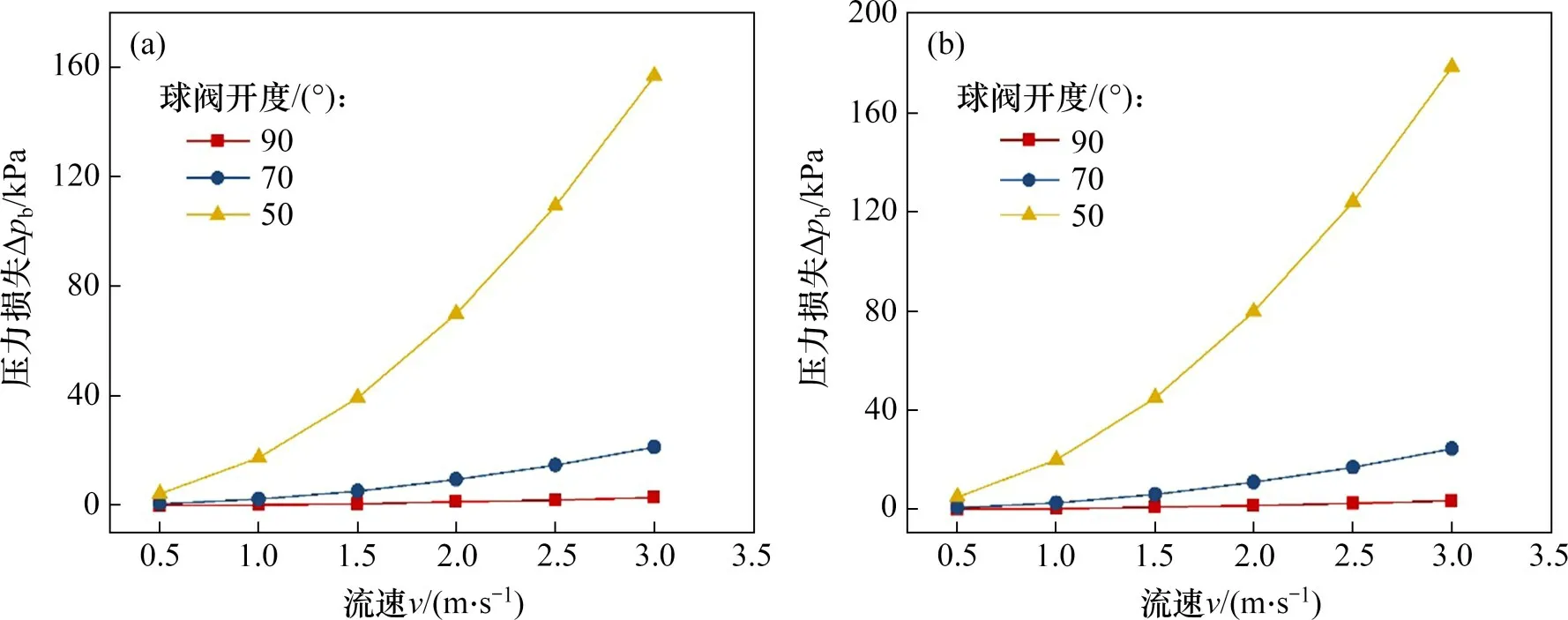
图8 球阀两相流压力损失随进口流速的变化Fig.8 Variation of pressure loss of solid-liquid two-phase flow of PVC ball valves with flow velocity

3.3.3 球阀压力损失随球阀开度的变化

DN75 球阀在颗粒粒径为0.08 mm、颗粒体积分数为10%和20%时，球阀两相流压力损失Δpb随球阀开度的变化如图9所示。从图9可以看出：球阀开度对压力损失的影响明显，随着开度增大，压力损失减小；开度越小，压力损失的增加幅度越大。这是由于当开度较小时，进入球阀的流动受阻，阀芯内的流速梯度较大，湍流紊动剧烈，在阀芯和阀后部位出现较大的回流区域，使得液相损失和固相损失都增大，形成了球阀前后较大的压力损失。

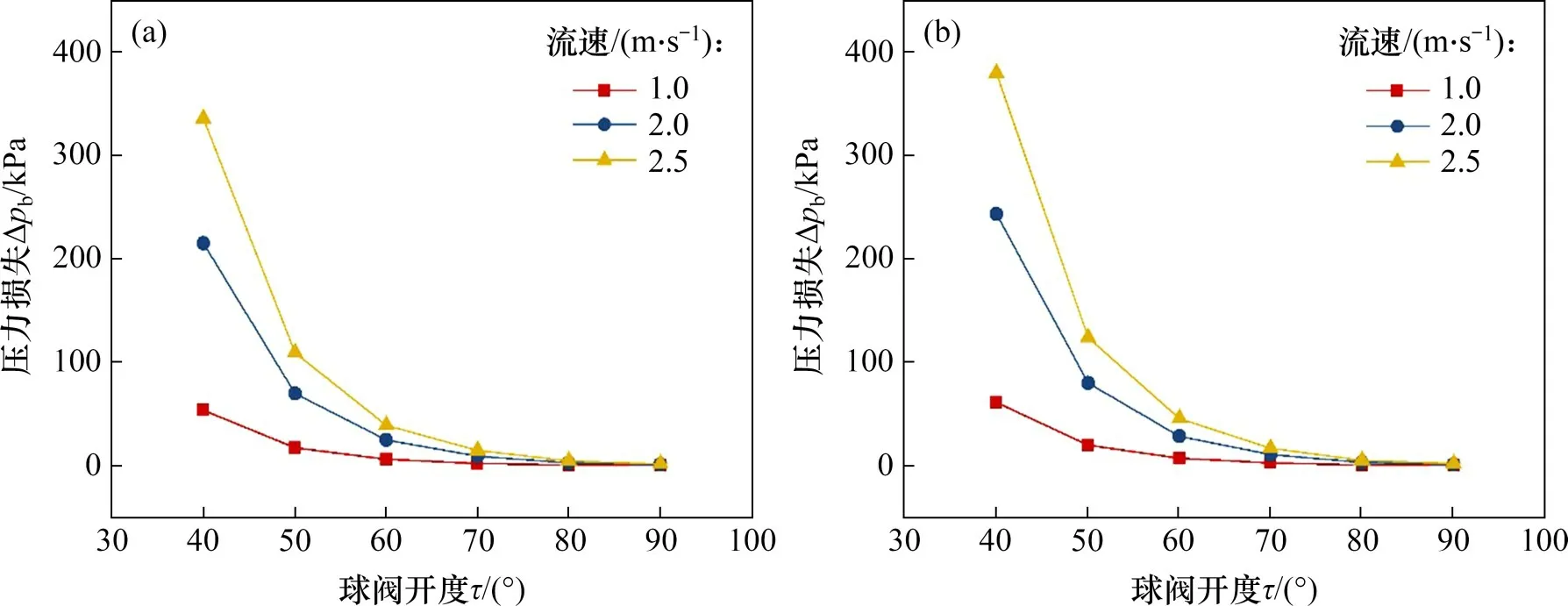
图9 液相两相流压力损失随球阀开度的变化Fig.9 Variation of pressure loss of solid-liquid two-phase flow of PVC ball valves with ball valve opening

3.3.4 球阀压力损失随颗粒体积分数的变化

当进口流速为2 m/s、颗粒粒径为0.05 mm 和0.12 mm、球阀开度为90°和50°时，液相两相流压力损失Δpb随颗粒体积分数的变化如图10所示。从图10可以看出：在其他条件不变时，压力损失随颗粒体积分数增大而增大；从变化幅度来看，颗粒体积分数对压力损失的影响不如流速和阀门开度对压力损失的影响明显。这是由于影响压力损失的固相和液相中，在颗粒体积分数较小时以液相损失为主，而固相损失较小；随着颗粒体积分数增大，固相颗粒数量增多，压力损失以固相损失为主，此时，液相损失较小。由于固相颗粒与管壁的摩擦碰撞引起的损失大于液相引起的损失，因此，当颗粒体积分数较大时，混合流的压力损失较大。

图10 液相两相流压力损失随颗粒体积分数的变化Fig.10 Variation of pressure loss of solid-liquid two-phase flow of PVC ball valves with particle volume fraction

3.3.5 球阀压力损失随颗粒粒径的变化

当进口流速2 m/s、颗粒体积分数为10%和20%、开度不同时，球阀压力损失Δpb随颗粒粒径的变化如图11所示。从图11可以看出：在开度为70°～90°时，压力损失随着颗粒粒径增大略有增大；而在开度为40°～60°时，压力损失随着颗粒粒径增大而有所减小，整体上变化幅度不大；当颗粒体积分数不变时，增大颗粒粒径使颗粒的数量减小，在开度为70°～90°时，由于球阀开度较大，流动相对平顺，在阀芯和阀后产生的回流区域较少而湍动能较弱，此时，压力损失主要取决于颗粒运动(包括颗粒与颗粒、颗粒与水流的作用)；当颗粒粒径增大时，粒径大而数量少的颗粒运动所消耗的能量大于粒径小而数量多的颗粒运动所消耗的能量，因而，随着粒径增大，压力损失增大；在开度为40°～60°时，由于开度较小，进入球阀的流动紊动剧烈，在阀芯和阀后部位产生的回流区域增多，回流使颗粒与壁面之间的碰撞剧烈程度加大，此时，当颗粒粒径增大时，压力损失可能取决于颗粒与壁面之间的作用，粒径小而数量多的颗粒与壁面之间的碰撞力大于粒度大而数量少的颗粒碰撞力，可能造成小开度时压力损失随粒径的增大而减小。

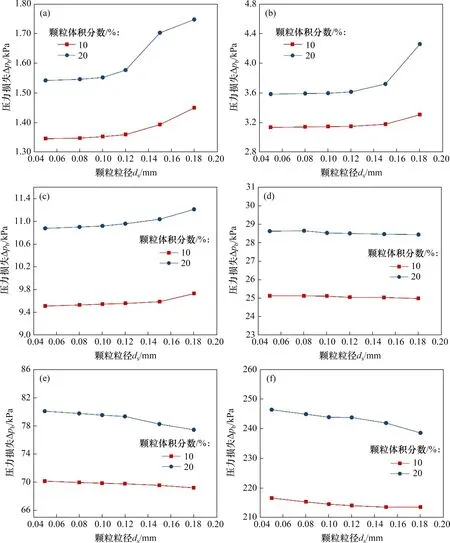
图11 球阀压力损失随颗粒粒径的变化Fig.11 Variation of pressure loss of ball values with particle size

3.4 压力损失变化影响因素评价

为了进一步探讨不同影响因素对球阀压力损失的影响程度，采用无交互作用的单因变量多因素方差分析法进行评价，分析不同影响因素的显著程度。

单因变量多因素方差分析是研究多个因素对同一因变量的影响水平的统计方法，对某一因变量，假设有m个影响因素，记为A1,A2,…,Am，因素Ai有ri个水平(i=1,2,…,m)，若记该因变量为Xk1k2…km，则该多因素方差分析的数学模型为[19]

式中：μ为总均值；αki为因素Ai的水平效应；εk1k2…km为随机误差，各个εk1k2…km相互独立且服从N(0,σ2)；k1=1,2,…,r1；k2=1,2,…,r2；km=1,2,…,rm。

以DN75 球阀固-液两相流压力损失Δpb为考察对象，采用F检验法对影响压力损失的4个因素(进口流速v、球阀开度τ、颗粒体积分数n和颗粒粒径ds)进行多因素方差分析，结果如表1所示(检验假设所有因素对压力损失Δpb没有显著性影响)。

取检验显著性水平α=0.05。从表1可以看出：颗粒体积分数和颗粒粒径的相伴概率P分别为0.848 和1.000，均大于0.050，表明颗粒体积分数和颗粒粒径对压力损失的影响不显著；而进口流速和球阀开度的相伴概率P均小于0.050，表明进口流速和球阀开度对压力损失具有显著影响。由于球阀开度的相伴概率远小于进口流速的相伴概率，因此，球阀开度对压力损失的影响最显著。

表1 影响因素方差分析结果Tab.1 Results of variance analysis for influenced factors

4 讨论

影响球阀固-液两相流压力损失的因素较多，本文主要讨论进口流速、球阀开度、颗粒体积分数和颗粒粒径对DN75PVC 球阀压力损失的影响。本研究中，压力损失随流速增大而增大，这与文献[18]所得的水平管道中冰水两相流压力损失一致。在球阀与水平管道中，当速度增大时，水流与颗粒的紊动都加剧，因而损失增大。压力损失随球阀开度增大而减小，这是由于开度增大时流通能力增强，流速梯度减小，压力损失也减小。压力损失随颗粒体积分数增大而增大，这与文献[20]所得的水平管道中固-液两相流结果一致。在水平管道中，颗粒数量增多，增加了颗粒之间的碰撞概率，而且较多数量的颗粒维持悬浮需要提供的能量也多；而在球阀中，由于流体面积较小，颗粒数量较多时增加了颗粒与颗粒、颗粒与壁面的碰撞概率。颗粒粒径的变化对压力损失的影响较复杂。文献[20]得出在其他条件不变时，水平管道中的压力损失随粒径增大而增大；而文献[18]得出冰水两相流压力损失随粒径增大而减小；在球阀中，当开度为70°～90°时，压力损失随粒径增大而增大；当开度为40°～60°时，压力损失随粒径增大而减小。粒径增加可能使压力损失增加，也可能会降低，具体取决于颗粒的运动特性及流通边界。