微重力下液氢流动沸腾的气泡脱离特性
2021-06-21郑尧常华伟陈虹舒水明
郑尧,常华伟,陈虹,舒水明
(1.航天低温推进剂技术国家重点实验室,北京,100028;2.华中科技大学能源与动力工程学院,湖北武汉,430074)
液氢作为一种低温推进剂,具有高比冲、无污染等特点。为完成远距离星际探测任务,需要对液氢进行在轨加注[1]。在加注系统中不可避免地存在漏热现象,因此,加注管内液氢以流动沸腾的气液两相形式进行传输[2]。影响管内氢两相流动的因素包括管径、流速、壁面粗糙度、管路振动等[3-7]。在微重力下,液氢在流动沸腾过程中的气泡脱离特性会发生明显变化,造成其流动传热特性与常重力下的有较大差异[8-11]。研究微重力下氢气气泡脱离特性,对建立微重力下精确的流动传热模型进而研究液氢在微重力下流动传热特性具有重要意义。气泡从其成核点脱离,在流动沸腾过程中扮演着重要角色,在RPI 沸腾模型中,对流、蒸发、急冷3部分换热量均与气泡的脱离直径有关[12],准确计算沸腾传热系数,需要精确的气泡脱离直径模型。然而,RPI沸腾模型中所用的气泡脱离模型为经验/半经验公式[13-16],一方面,该模型受工质物性的影响,其在低温下的适用性有待进一步考证;另一方面,已有的经验公式均为池沸腾实验所得,当流动沸腾中引入流速后,上述模型也需要进一步修正。因此,许多学者以沸腾时单个气泡在生长过程中的受力分析为切入点,建立不同工质在沸腾过程中气泡脱离直径模型,并阐明了气泡脱离机制[17-20]。在微重力下,流动沸腾过程中气泡的生长及脱离与常重力下呈完全不同的规律。KARRI[21]建立了微重力下池沸腾气泡脱离模型,其计算结果与实验测量值吻合良好,同时他指出表面张力在微重力下对气泡的脱离起主要阻碍作用。马原等[22]以微重力下液氢池沸腾中的气泡为研究对象,并考虑温度分布不均造成的马兰戈尼效应,建立了气泡脱离模型,他们发现微重力下气泡脱离直径远比常重力条件下的直径大。高旭等[23]在池沸腾的基础上,引入气泡切向受力,建立了微重力下流动沸腾过程中气泡的受力模型,当工质流速足够大时,气泡脱离直径在微重力与常重力条件下的差别可以忽略。精确地计算微重力下液氢加注过程中的流动传热是保证高质量在轨加注的关键,气泡脱离直径作为液氢流动沸腾中的一个重要参数,与流动沸腾过程中的热质传递密切相关。现阶段,通过实验所得的经验公式的适用范围仍有待验证,因此,建立精确的脱离直径模型至关重要。本文作者对流动沸腾过程中产生的单个氢气气泡进行受力分析,建立微重力及常重力条件下气泡脱离直径模型,对比研究不同重力条件下流速、壁面过热度、表面张力及压力等对气泡脱离直径的影响规律,研究结果可为微重力下液氢管内的流动沸腾过程研究提供参考。
1 液氢流动沸腾的气泡脱离模型
1.1 气泡脱离模型及受力分析
对气泡脱离过程进行建模前,进行如下主要基本假设:1)当气泡脱离时,气泡之间相互无影响,因此,选用单个气泡进行受力分析;2)忽略气泡的生长脱离对主流速度的影响,认为液相的主流速度为定值;3)气泡周围的液体处于饱和状态。
在研究过程中,加热壁面为具有一定过热度的恒温壁面,壁面温度为23.5 K。对直径为Db的氢气气泡进行受力分析,如图1所示,其中,氢气气泡在法向的受力主要有浮升力Fb、剪切升力Fsl、接触压力Fcp、水动压力Fh、表面张力Fst以及非稳态曳力Fdu;在切向的受力主要包括准稳态曳力Fqs、表面张力Fst以及非稳态曳力Fdu;Dw为接触直径,m;U为流速,m/s。由图1可见:气泡切向受力Fx=Fst,x+Fqs+Fdusinγ,法向受力Fy=Fst,y+Fsl+Fducosγ+Fb-Fh+Fcp,其中,γ为非稳态曳力与重力加速度g的夹角。

图1 氢气气泡受力分析Fig.1 Stress analysis of a hydrogen bubble
在流动沸腾过程中,气泡所受的浮升力和剪切升力分别可以表示为:

气泡在生长过程中,气泡的半径R满足如下方程:

雅克比数Ja即显热与潜热之比,为衡量壁面过热度的量纲为一的参数,定义如下:

式中:ρl和ρv分别为液相和气相的密度,kg/m3;g为重力加速度,m/s2;CL为剪切升力系数;η为液体热扩散率,m2/s;t为时间,s;cpl为液相比定压热容,J/(g·K);ΔTsup为壁面过热度,K;hfg为液氢的汽化潜热,J/g。
气泡生长过程中会受到壁面的接触压力Fcp与液体的水动压力Fh的作用,即
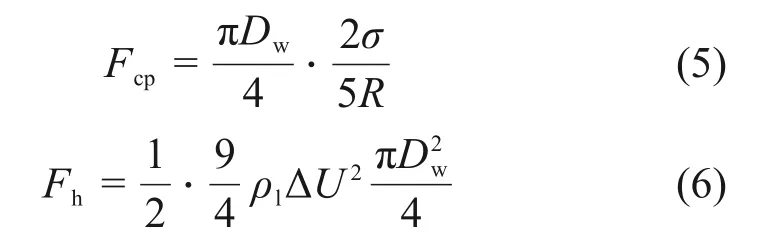
式中:Dw=0.002 5Db;σ为表面张力系数,N/m。
气泡所受的非稳态曳力Fdu和准稳态曳力Fqs分别为:

雷诺数Reb定义为

切向和法向的表面张力分量可由下式进行计算:
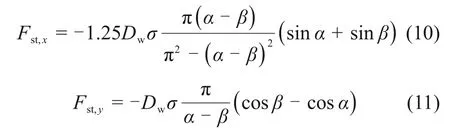
式中:υl为液相黏度,m2/s;α和β分别为气泡与壁面的前接触角和后接触角,rad。
从上述分析可知,气泡从加热壁面的脱离是切向受力与法向受力综合作用的结果。当受力平衡时气泡处于脱离状态的临界点即满足Fx=0时,气泡开始沿加热壁面滑移;当满足Fy=0 时,气泡离开加热壁面升起。根据上述气泡脱离模型,对气泡的升起直径和滑移直径进行求解,取两者较小值即为气泡脱离直径。
1.2 模型验证
为验证所建立的气泡脱离模型的准确性,本文将模型计算得到的气泡脱离直径与文献[24-25]中测量的实验结果进行对比,如图2所示。由图2可见:在常重力环境下,R113 流动沸腾过程中气泡脱离直径的实验结果与本模型的模型计算结果基本吻合,除个别点外,最大相对误差保持在±30%以内,平均相对误差为19.8%;在不同重力加速度下,气泡脱离直径实验与模拟结果的平均相对误差为8.7%。考虑到实际测量中的难度以及建模过程中的假设,认为所建立的气泡脱离模型是准确的,可用于计算与分析常重力及微重力下氢气气泡脱离直径。

图2 气泡脱离直径计算值与实验值对比Fig.2 Comparisons between calculated and experimental results of bubble departure diameter
2 结果与讨论
2.1 重力加速度对气泡脱离直径的影响
气泡的生长受法向与切向作用力的共同约束,法向上,浮升力、剪切升力、接触压力为气泡脱离的动力,表面张力、非稳态曳力及水动压力为阻力,其中浮升力与重力加速度有关,剪切升力与流速有关。当气泡法向所受动力比阻力大时,气泡便会沿法向从壁面脱离。不同流速下气泡升起直径随重力加速度的变化如图3所示。由图3可见:当液氢流速较低时,气泡升起直径随重力加速度的减小而增大。当雷诺数Re为1 329时,微重力(10-4g)下气泡升起直径比常重力(g)的气泡升起直径增大了约7 倍,而当雷诺数增大到2 659 时,其升起直径增大约3倍。此外,气泡升起直径呈“两头平,中间陡”的变化趋势,当重力加速度为(10-3~10-1)g(1g=9.8 m2/s)时,气泡升起直径受重力加速度的影响较大,而当重力加速度非常小(<10-4g)或非常大(>g)时,气泡升起直径的变化趋于平缓。当流速逐渐增大时,气泡所受的剪切升力逐渐增大直至成为影响气泡脱离的主要因素,重力加速度的变化对气泡升起直径的影响逐渐减小,此时,气泡升起直径在不同重力条件下几乎相同。
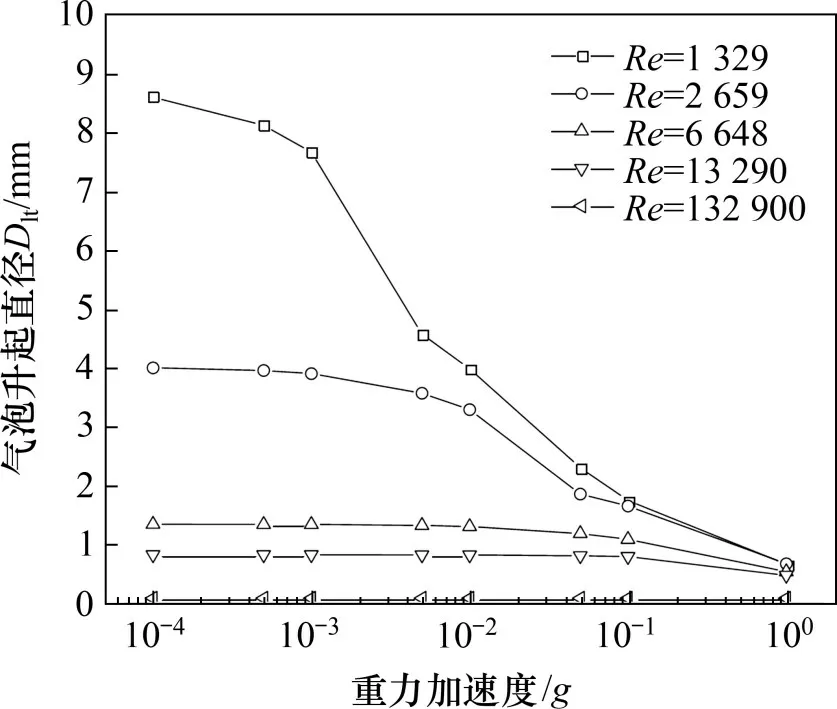
图3 气泡升起直径随重力加速度的变化Fig.3 Variation of bubble lift-off diameter with gravitational acceleration
切向上,准稳态曳力为气泡滑移的动力,而表面张力与非稳态曳力为滑移的阻力,当滑移动力大于阻力时,氢气气泡在切向上沿加热壁面滑移。图4所示为不同液氢流速下气泡滑移直径的变化。由图4可知:随流速增大,气泡的滑移直径逐渐减小,当流速大于0.1 m/s 时,气泡滑移直径几乎保持不变;在微重力条件下,当流速较低时,尽管气泡的升起直径与滑移直径均较大,但滑移直径仍明显比其升起直径小,此时气泡先离开其成核位置,在切向上沿壁面滑动直至满足升起条件时沿法向脱离壁面;在较高流速情况下,气泡的升起直径比滑移直径略小,此时气泡将优先沿法向脱离壁面。同样地,在常重力条件下,无论流速高低,气泡的升起直径均比滑移直径小,气泡均将优先沿法向脱离壁面。
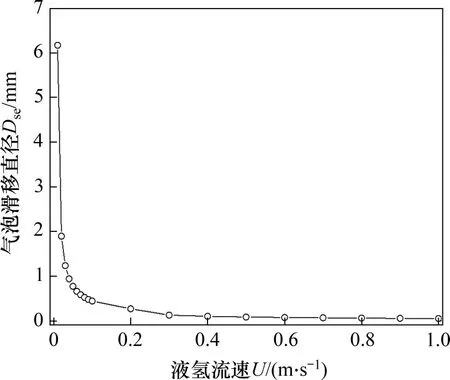
图4 气泡滑移直径随液氢流速的变化Fig.4 Variation of bubble slide diameter with velocity
2.2 壁面过热度对气泡脱离直径的影响
雅克比数与气泡的生长密切相关,当雅克比数较大时,气泡生长较快,反之则较慢。图5所示为当流速为0.01 m/s,壁面过热度为5 K 时,不同重力条件下气泡升起直径随雅克比数的变化。从图5可以看出:气泡升起直径随壁面过热度的增大而增大。这是因为随壁面过热度增大,非稳态曳力逐渐增大,气泡所受的阻力变大,气泡升起直径增大;同时,在微重力条件下,气泡升起直径对壁面过热度的变化更为敏感,这是因为在微重力条件下,气泡所受的浮升力远比常重力条件下所受的浮升力小,气泡所受的非稳态曳力由影响气泡脱离的次要因素上升为主要因素,即微重力下气泡的脱离与壁面过热度密切相关。

图5 不同重力条件下气泡升起直径随雅克比数变化Fig.5 Variation of bubble lift-off diameter with Jacobi Number under different gravity conditions
2.3 表面张力系数对气泡脱离直径的影响
图6所示当流速为0.01 m/s,壁面过热度为5 K时,微重力(10-4g)与常重力(g)下气泡升起直径随表面张力系数的变化。由图6可见:随表面张力系数增大,微重力及常重力条件下气泡升起直径均增大,这是因为表面张力阻碍气泡脱离受热壁面,且表面张力越大,气泡越不易脱离受热壁面。同时,接触压力与表面张力系数密切相关,接触压力在气泡脱离过程中起促进作用。然而,当表面张力系数增大时,接触压力增大,此时氢气气泡升起直径依然增大,这也反映了与表面张力相比,接触压力在气泡脱离过程中的作用较小。在微重力条件下,气泡升起直径受表面张力的影响更为明显,其随表面张力系数的变化基本呈线性增大的趋势;在常重力条件下,浮升力占主导作用时气泡升起直径受表面张力的影响十分微弱。上述分析表明,微重力条件下缺少重力引起的浮升力的作用,表面张力作为抑制气泡脱离的作用力在气泡脱离的过程中起到更为关键的作用。
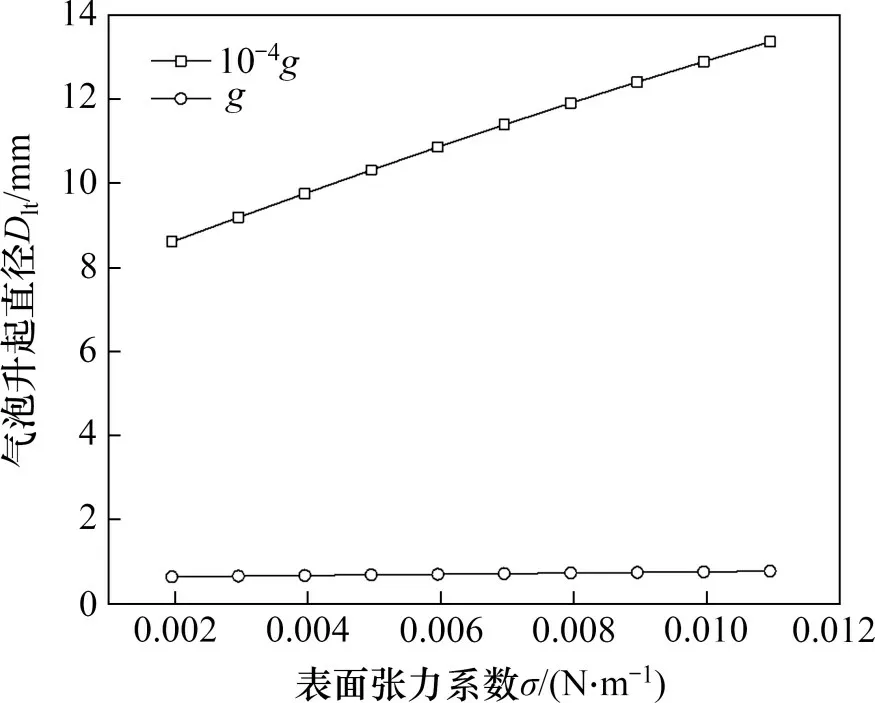
图6 不同重力条件下气泡升起直径随表面张力系数变化Fig.6 Variation of bubble lift-off diameter with surface tension coefficient under different gravity conditions
2.4 压力对气泡脱离直径的影响
通过对气泡的受力分析可知,氢气气泡升起直径的确定与气液两相的密度、比热容、导热系数、表面张力系数等物性相关,而这些参数与压力有着密切的联系。图7所示为微重力与常重力下,气泡升起直径随压力的变化。由图7可见:在不同重力下,气泡升起直径均随压力的增大而减小,其主要原因是随压力增大,表面张力系数逐渐减小,导致表面张力减小,从而气泡更容易脱离壁面,因此,在微重力条件下,气泡升起直径随压力的变化更为明显。
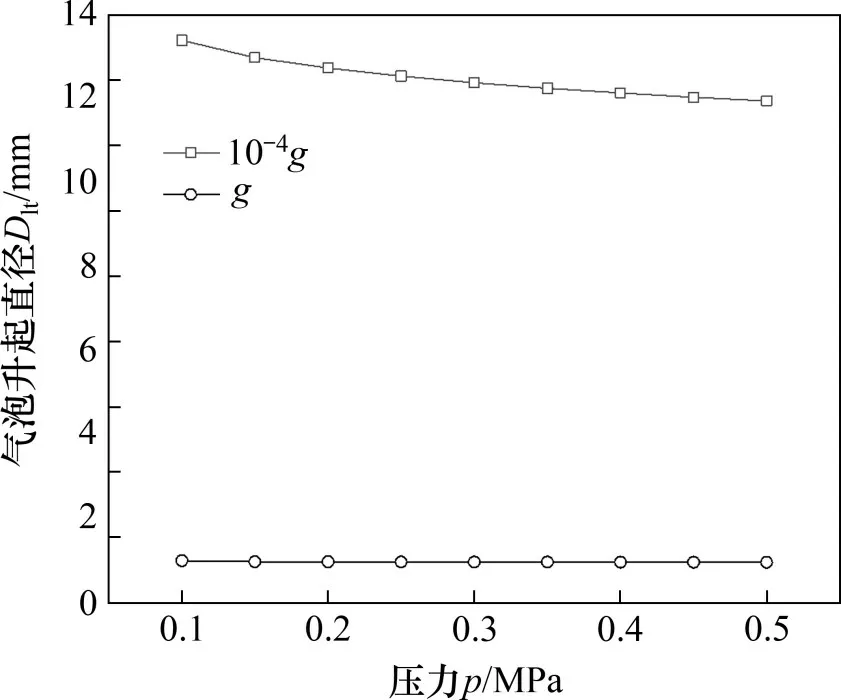
图7 不同重力条件下气泡升起直径随压力变化Fig.7 Variation of bubble lift-off diameter with pressure under different gravity conditions
3 结论
1)在低流速条件下,随重力减小,氢气气泡升起直径逐渐增大;相反,在高流速下,氢气气泡升起直径随重力加速度变化不明显。同时,提高流速可有效减小氢气气泡滑移直径。
2)在微重力低流速条件下,氢气气泡首先会以滑移的形式离开其成核点,之后再脱离加热壁面;在微重力高流速下,氢气气泡先脱离加热壁面;在常重力低流速及常重力高流速下,氢气气泡将优先脱离加热壁面。
3)在微重力条件下,由重力加速度引起的浮升力作用几乎可以忽略,此时,壁面过热度、表面张力系数及压力等参数的变化所引起的其他受力的变化在微重力条件下对氢气气泡脱离的作用更强。
