基于文丘里管原理式叶片的离心泵空化特性研究

2021-06-21赵伟国路佳佳赵富荣李清华

中南大学学报（自然科学版） 2021年5期

赵伟国，路佳佳，赵富荣，李清华

(1.兰州理工大学能源与动力工程学院，甘肃兰州，730050；2.甘肃省流体机械及系统重点实验室，甘肃兰州，730050)

据统计，在各种类型的泵产品中，离心泵占据约80%的市场份额[1]，所以，对离心泵内流动进行深入研究具有极其重要的作用。然而，离心泵运行过程中存在的畸变流[2]严重影响了其性能，空化流便是其中一种最重要的畸变流形式。空化流对离心泵运行性能的影响主要表现在3个方面：

1)泵性能下降。离心泵内发生空化现象时，空穴导致流体的能量交换受到影响，积聚的空穴造成泵扬程大幅度下降，叶轮丧失做功能力[3]。

2)离心泵的非定常特性增强，导致离心泵运行状态极不稳定。当离心泵内空化发生时，空穴在低压区产生、脱落，被主流流体输运到高压区，高压流体的挤压作用导致空泡溃灭，溃灭过程产生的强烈冲击波导致离心泵内出现明显的振动和噪声[4]。研究表明，在泵进口注入空气可以缓冲空化产生的振动、噪声[5]。

3)空泡溃灭时产生的高频冲击可达25 kHz，压力可达49 MPa[6]，对固壁表面产生严重侵蚀，影响了泵的使用寿命。

为延迟离心泵内空化初生和抑制空化泡发展，首先要了解离心泵内空化流的发生及发展机理。离心泵叶轮内主要的空化形式为叶片前缘空化[7]，一般在叶片进口边附近产生，并且会随着泵进口压力的不断降低逐渐由游离的微小气泡发展成为附着的片空化状态[8]。根据离心泵内空化现象的发展过程，可将其分为3个主要阶段，即初生空化阶段、弱空化阶段和剧烈空化阶段。当泵进口压力下降，叶轮内局部压力下降到该温度下的饱和蒸汽压以下时，叶片进口边附近会产生微小气泡，并在此区域溃灭，这一阶段称为空化初生阶段[9]。离心泵在此工况下运行时，叶片做功能力不受空化泡影响，但空化泡会导致离心泵运行时的稳定性变差，同时，微小空化气泡的溃灭导致叶片表面出现点蚀[10]，影响离心泵的使用寿命。在弱空化阶段，空化泡形态较稳定，在叶轮中的位置也相对固定，但叶轮内空化状态处于此阶段时会诱发叶轮内强烈的非定常特性。当泵进口压力再次降低时，到达剧烈空化阶段，大量空化泡的存在对叶轮内流体的能量交换能力产生明显影响，导致叶片工作能力下降，泵扬程骤降[11]。

基于空化发生及发展的机理，一些学者采取一些有效的方法控制离心泵内空化的发生及发展，如朱兵[12]提出了缝隙引流叶片抑制叶轮内空化的方法，即在叶片前缘添加偏置小叶片，将主流流体分成2部分，其中，一部分按原流动轨迹流动，另一部分流向叶片进口背面空化发生区，以提高叶片背面的压力，从而控制空化的发生及发展。数值模拟结果和试验研究结果表明，偏置小叶片结构能够对叶轮内空化产生明显的抑制效果，有效提高离心泵的空化性能；张文著等[13]研究了缝隙引流叶片内的振动特性及压力脉动特性，发现这种形式的叶片可降低离心泵叶轮内部的压力脉动及二次流输送效应，表明在抑制离心泵内空化发展的同时也使叶轮内的空化泡更加稳定，空穴震荡减弱，叶轮内非定常性减弱；赵伟国等[14]将在翼形表面布置障碍物抑制空化的理论应用到离心泵的空化研究中，发现此方案在离心泵中同样能起到抑制空化的作用，其主要机理在于当叶轮内空化状态处于云空化时，障碍物可以有效阻挡云空化所产生的回射流，从而对叶轮内空化产生有效的抑制作用，并且增加了叶轮内空化泡的稳定性，降低了叶轮流道内的压力脉动；胡赞熬等[15]对低比转速离心泵进口边开孔形式的叶片进行了研究，发现开孔可以有效降低叶轮进口环量，使得离心泵的扬程和效率都有所提高，同时，压力面流向吸力面的高压流体可以提高叶片背面的压力，抑制空化流。为此，本文作者在前人研究成果基础上，设计几种基于文丘里管原理的叶片，并分析文丘里管喉部几何参数与空化抑制效果的关系。

1 数值求解方法

1.1 控制方程

流体流动过程中所采用的控制方程如下。

连续性方程：

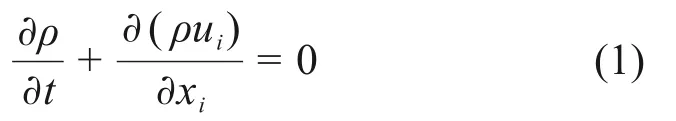
动量方程：

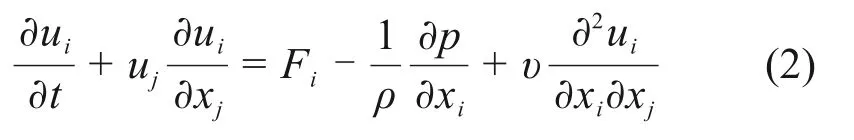
式中：i=1，2，3；j=1，2，3；ui和uj为流体速度分量，m/s；xi和xj为坐标轴分量；ρ为流体密度，kg/m3；p为压力，Pa；υ为运动黏度系数，m/s2；Fi为质量力，m/s2；t为时间，s。

1.2 湍流模型

单相计算采用Standardk-ε湍流模型进行计算，待计算结果收敛后，以单相计算的结果为初值再次对空化条件下的流场进行计算。采用修正的SSTk-ω湍流模型[16]进行空化计算。对SSTk-ω湍流模型修正的方法主要是通过密度函数f(ρ)代替密度ρ，方程式见式(3)和式(4)，湍流黏度修正函数变化曲线如图1所示。

图1 湍流黏度修正函数曲线Fig.1 Correction function curves of turbulent viscosity

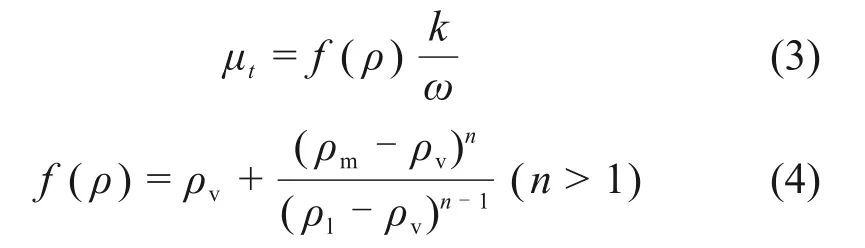
式中：k为湍流能，m2/s；ω为耗散率；ρv为气相密度，kg/m3；ρl为液相密度，kg/m3；ρm为气液混合相密度，kg/m3；n为常数。

研究结果表明[17-18]，在空化计算过程中，当n取10 时，湍流黏度计算结果和实验结果更吻合，故本文计算过程中取n=10。

1.3 空化模型

在空化计算过程中采用KUBOTA 等[19]提出的空化模型，又称ZGB(Zwart Gerber Belamri)空化模型。该模型是在泡动力学方程Rayleigh-Plesset[20]的基础上发展而来的，泡动力学方程为

式中：RB为空泡半径，m；σ为表面张力系数；pv为气泡压力，Pa。

空化过程中气液两相之间的传质率S如下所示：

当p＜pv时，

当p＞pv时，

式中：Fvap为蒸发系数，取50；Fcond为凝结系数，取0.01；RB取10-6m；rv为气泡体积分数；rnuc为气化核心气泡体积分数，取5×10-4。

1.4 数值算法验证

通过实验值与模拟值对比分析，判断数值仿真结果的准确性。实验在甘肃省流体机械及系统重点实验室搭建的离心泵水力测试系统上完成，离心泵可视化实验平台如图2所示，实验系统主要包括压力罐、直径×高度为1 200 mm×1 600 mm 的气蚀罐、电磁流量计、有机玻璃制成的可视化离心泵、扭矩仪、三相异步电动机及各种阀门及管道。在额定转速下的全流量运行状态实验中，泵的流量工况点由出口阀门控制；空化实验通过真空泵降低闭式管路系统的进口压力，从而使离心泵内发生空化。

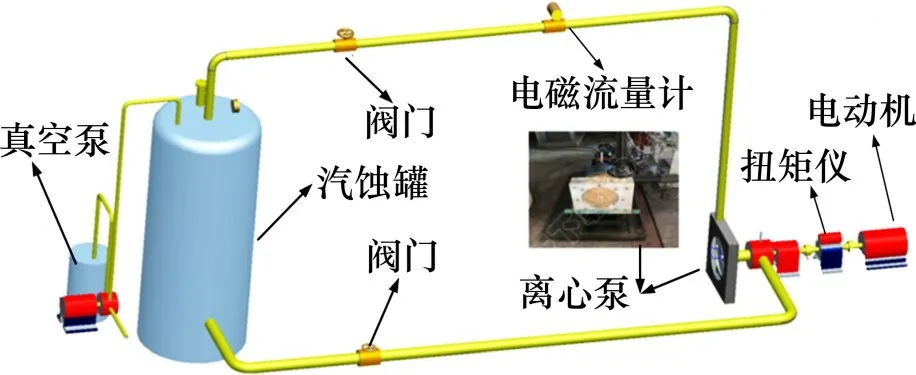
图2 离心泵可视化实验平台Fig.2 Visualization experimental platform of centrifugal pump

图3所示为不同流量下扬程和效率数值模拟结果与实验结果对比(图中Q为流量，Q0为额定定工况点的流量)。从图3可以看出：当流量为1.2Q0时，扬程和效率相对误差均最大，扬程相对误差为4.86%，效率相对误差为4.82%。综上所述，对于非空化流场，扬程和效率相对误差均在5.00%以内，可满足精度要求，说明该数值模拟方法可用于计算离心泵内非空化流场。

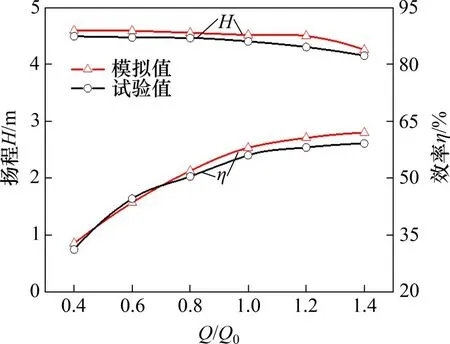
图3 外特性对比曲线Fig.3 Comparison curves of external characteristics

装置空化余量又称空化余量，是指泵进口处单位质量液体具有的总水头减去单位质量液体的气化压力水头，国外将其命名为有效净正吸头，指泵进口液体的全水头减去气化压力水头，一般用HNPSa表示，表达式如下：

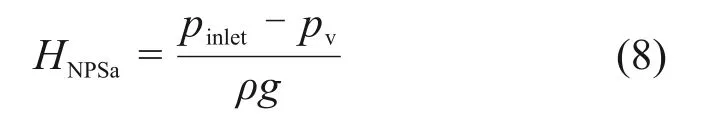
式中：pinlet为泵进口总压，Pa；pv为饱和蒸汽压，本文中取纯水25 ℃时的饱和蒸汽压3 169 Pa。

图4所示为不同空化余量下扬程实验值与模拟值的空化特性曲线对比结果。从图4可见：在未发生空化的工况下，扬程模拟值稍高于实验值，这与计算非空化流时得到的结果相近；当叶轮发生空化时，在扬程断裂点误差最大为3.7%。总体而言，扬程数值模拟结果与实验结果较吻合，此模拟方法可用于后续计算。

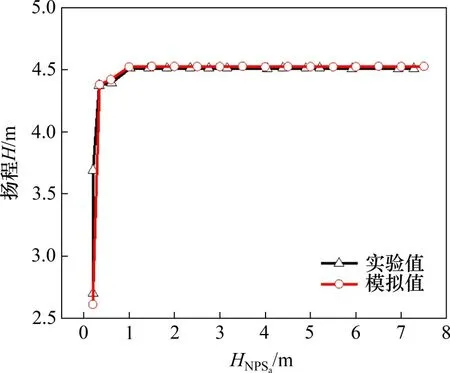
图4 空化特性对比曲线Fig.4 Comparison curves of cavitation characteristics

2 物理模型及数值求解

2.1 物理模型及计算网格

本文主要研究比转速为32 时的单级单吸离心泵。模型泵主要参数如下：流量为8.6 m3/h，转速为500 r/min，叶片数为6 片。水体三维造型如图5所示。

图5 水体域三维造型Fig.5 Three-dimensional modeling of water body

在数值计算过程中，网格质量及网格形式是影响计算结果精准性的主要因素。物理结构较简单的进口段、腔体、叶轮采用六面体结构网格；而对于具有复杂外形构造的几何体蜗壳，建立空间拓扑关系较困难，且结构化网格质量较低，故选择能够适合复杂几何构造的四面体非结构网格。计算域三维网格如图6所示。为避免网格数量引起计算结果的误差，设计3种不同密度的网格进行无关性检验，计算结果如表1所示。考虑到经济性与准确性2 个方面的因素，最终确定中等数量的网格，即采用总网格数为2 077 156 个进行后续计算。

图6 计算域三维网格Fig.6 Three-dimensional grid of computational domain

表1 网格无关性检验Table 1 Check of grid independence

2.2 基于文丘里管原理的叶片几何模型

模型几何结构如图7所示。从图7可以看出叶片的缝隙有一个先从大变小后从小变大的过程，这一结构与文丘里管的结构极其相似，因此，其内部流动与文丘管内的流动相似。离心泵是用来提高液体压力的水力机械，其工作原理是通过叶片的旋转过程将动能转换成压力势能。随着流体向叶轮出口流动，叶轮内流体压力不断升高，为了使文丘里管射流结构对叶轮内空化发展起到有效的抑制作用，在压力相对较高且距空化发生区位置较近的区域即叶片中部设置文丘里管式射流结构。文丘里管喉部几何参数是影响其工作效率的关键因素，将此原理应用到离心泵空化控制中时，喉部几何参数对空化流的影响尤为明显。喉部深度参数定义为

图7 模型几何结构Fig.7 Model geometries

式中：h为缝隙深度；d为缝隙处叶片的轴向宽度。

模型几何数据如表2所示。

表2 模型几何数据Table 2 Model geometry data

2.3 边界条件及求解策略

计算结果的准确性除了受网格参数的影响外，边界条件的设置也是影响计算结果的重要因素。在计算过程中，进口设置为压力进口，出口设置为质量流量出口，壁面采用无滑移边界；近壁面采用标准壁面函数处理，叶轮与进口和蜗壳的交接面设置为动静转子(rotor stator)。

进行非定常空化计算时，采用定常空化的计算结果为初值，动静交接面选择瞬态动静转子(transient rotor stator)，时间步长选择叶轮旋转3°为1个计算周期，即时间步长为0.001 s，计算总时长为1.2 s，即叶轮旋转10 圈，取最后1 圈的计算结果进行分析。

3 计算结果分析

3.1 外特性分析

计算4种不同模型的单相流场和空化流场。对于离心泵内的单相定常流动，计算0.4Q0，0.6Q0，0.8Q0，1.0Q0，1.2Q0，1.4Q0这6种工况下的扬程和效率(其中，Q0为计算流量)，计算结果如图8所示。从图8可见：带有文丘里管式射流结构的模型与原始模型的扬程和效率均相差不大，文丘里管式射流结构对离心泵性能影响较小，不会导致泵性能明显下降，从而不会影响离心泵的正常运行。空化曲线如图9所示。从图9可以看出：当空化余量大于1.0 m 时，不同叶轮模型的扬程相差不大；当空化余量为0.2～1.0 m时，叶轮内空化现象明显，导致泵扬程明显下降；在相同扬程下，改型叶轮结构的空化余量明显增加；当叶轮内空化状态到达剧烈空化状态即空化余量下降到0.2 m时，文丘里管式射流结构对叶轮内空化流的抑制效果显著，扬程均未出现明显断裂现象。从图9还可看出：对于不同的叶轮模型，当H1叶轮模型在空化余量为0.60 m和0.35 m时，扬程出现微小下降；当空化余量为0.20 m 时，泵扬程明显下降，但与原模型相比，下降量较小。综上所述，此结构对弱空化阶段及剧烈空化阶段都有明显抑制作用，能够明显提升离心泵在空化工况下的运行效率，其中，H1叶轮模型的提升效果最明显。

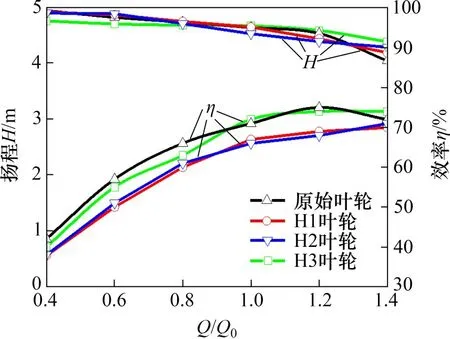
图8 外特性曲线Fig.8 External characteristic curves

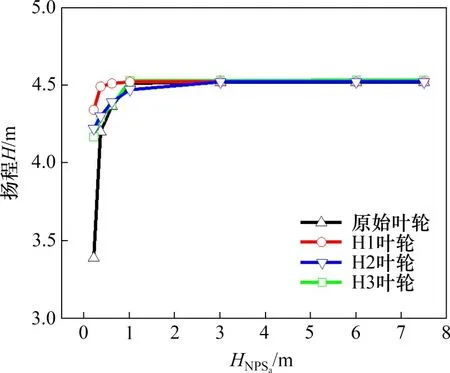
图9 空化特性曲线Fig.9 Cavitation characteristic curves

3.2 不同叶轮模型内空泡体积分数的变化

叶轮内空泡体积分数rimp定义为

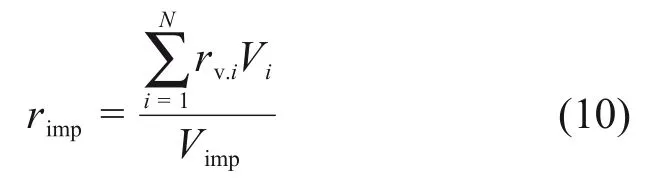
式中：N为叶轮内总控制单元数目；rv.i为第i个控制单元内气相体积分数；Vi为第i个控制单元体积；Vimp为叶轮体积。

空化体积分数变化如图10所示。从图10可以看出：当空化余量为1.0 m时，叶轮内空泡体积分数随叶轮旋转不断波动，但空泡体积分数的变化总体变化变化量较小；当空化余量为0.60 m 和0.35 m时，4种不同叶轮形式的空泡体积变化趋势基本一致，均是先增大后下降，但与原模型相比，文丘里管原理式叶轮能够有效地降低空泡的增加率，导致空泡体积分数的增长速率减小；当空化余量为0.20 m时，4种叶轮形式的空泡体积分数均逐渐下降，变化趋势基本一致。出现这种变化趋势与叶轮内空化流所处的空化状态有关，当空化余量为0.60 m 和0.35 m 时，叶轮内空化状态为弱空化状态，空化流极不稳定，射流作用导致这种不稳定性更加明显，从而对叶轮内空化的蒸发速率和凝结速度产生较大影响；而当空化余量为1.00 m 时，空化泡处于空化初生状态，空化量较小，射流不会产生较大变化；当空化余量为0.20 m时，为剧烈空化阶段，空化泡呈稳定的云空化状态，空化泡较稳定，射流增加了低压区能量，导致空泡体积分数发生明显变化，但射流引起的变化不足以导致空泡体积分数变化趋势产生较大变化。

图10 空化体积分数变化Fig.10 Volume fraction change of cavitation

在1个叶轮旋转周期内，文丘里管式射流结构对空泡体积分数的影响结果如表3所示。从表3可见：当空化余量为1.00 m时，处于空化初生阶段。所以，此阶段不能作为空化抑制作用的主要依据，故不对其进行分析。在弱空化阶段，即当空化余量为0.60 m 和0.35 m 时，叶片工作面与背面的压差较大，喉部的颈缩效应占主导地位，因此，H1模型的抑制效果最明显；当空化余量下降到0.20 m即叶轮内空化达到剧烈空化阶段时，H3 叶轮模型的空泡体积分数下降最明显。

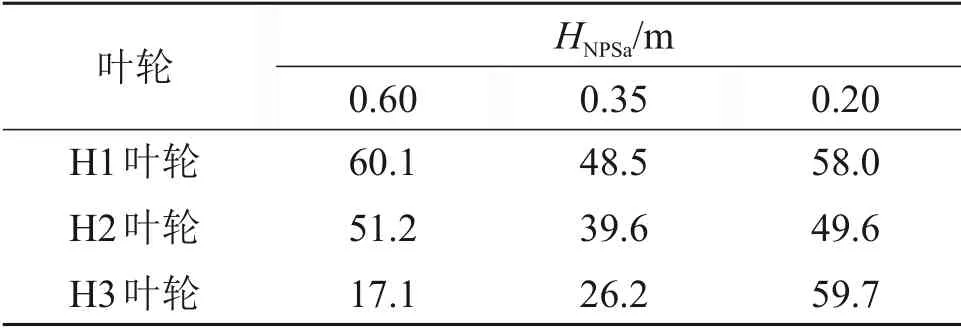
表3 空泡体积分数下降量Table 3 Volume fraction reduction of vapor %

3.3 非定常特性分析

定义叶片通过频率f为

式中：n为转速，r/min，本文取500；Z为叶片数，本文取6。经计算得f=50 Hz。

为分析基于文丘里管原理叶片对离心泵内瞬态空化特性影响，在叶轮内设置如图11所示的监测点P，监测流道内绝对压力的变化，并对1个周期内的压力进行快速傅里叶变换得到图12所示的压力频谱图。

图11 监测点位置Fig.11 Location of monitoring point

由于叶轮与蜗壳之间的动静干涉作用，监测点压力呈周期性变化，其变化规律与叶轮转速和叶片数有关。从图12可见：所有模型压力脉动主频为50 Hz，与叶频相等；原始叶轮与改变后的叶轮模型压力脉动频率变化特征的主频特性保持一致。

图12 压力频谱Fig.12 Frequency spectra of pressure

图13所示为不同模型不同空化数下的压力脉动主频幅值。从图13可见：当空化余量为1.0 m时，射流对流场产生优化作用，流动更加稳定，压力脉动主频幅值下降；而对于不同的射流结构，在此空化工况下，压力脉动主频幅值相差不大，即文丘里管喉部结构对空化初生状态的流体流动影响较小；当空化余量为0.60 m 和0.35 m 时处于弱空化阶段，与模型相比，监测点的主频幅值明显下降，其中，H1 模型的压力脉动主频幅值下降更加明显；当空化余量下降到0.20 m 即叶轮内空化达到剧烈空化阶段时，H3 叶轮模型的压力脉动主频幅值最小，这与叶轮内空泡体积分数的变化趋势基本一致。这说明此结构在减小空泡体积分数的同时，也使得空化泡的稳定性增加，空穴震荡减弱。

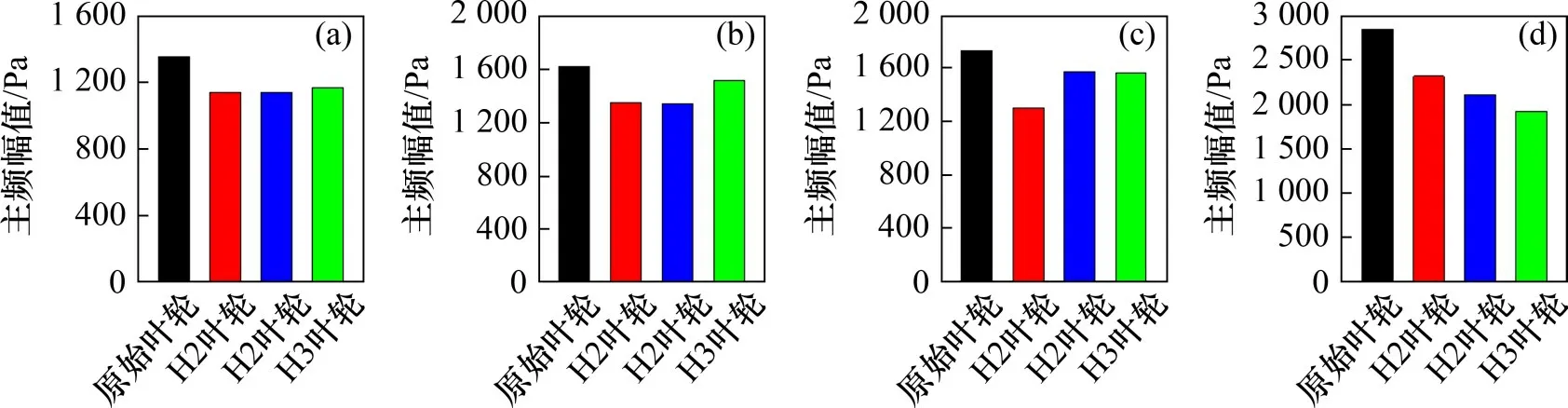
图13 压力主频幅值Fig.13 Amplitudes of dominate frequency of pressure

3.4 空化控制的内在机理

以H1 叶轮模型在空化余量为0.20 m 时的工况为例，研究此射流结构对离心泵空化流产生抑制作用的内在机理。

根据“饱和蒸汽压”理论，在水力机械运行过程中，当液体局部压力低于流体介质的饱和蒸汽压时，空化现象便会发生，所以，压力是影响离心泵空化现象发生的关键因素。叶片工作面的高压流体经基于文丘里管的射流结构流向叶片背面，改变了叶轮内的流场结构分布。叶轮不同截面压力分布见图14。从图14可以看出：叶轮内的低压区明显减小，与之相对应的空泡体积也明显减小，射流对叶轮内的空化现象产生了明显的抑制作用；同时，射流对叶轮内流场产生扰动，改变了叶轮内流动特性，这一特点表现在泵的性能参数即泵扬程和效率发生了变化。

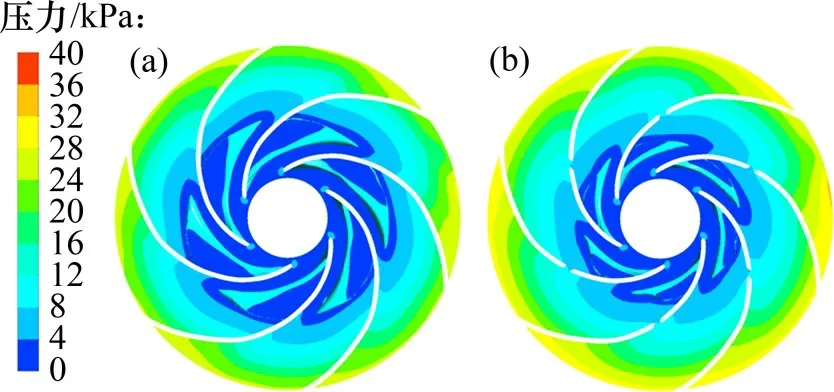
图14 叶轮不同截面压力分布Fig.14 Pressure distribution of different sections of impeller

速度作为反映流场流动最直观的参数，用于分析2种叶轮形式下的流动情况对研究空化抑制机理具有非常重要的意义。叶轮中截面速度分布见图15。从图15可以看出：叶片工作面的高压流体经射流结构流向叶片背面，射流出口区域的出现高速区导致叶片背面的附面层结构和失速涡旋结构发生改变，这影响了流道内的流体流动过程，进而导致叶轮空化泡析出规律发生变化。这种影响表现在涡结构的变化，如图16所示。从图16可以观察到高压高能对流场产生了明显的切割作用，导致射流孔出口涡量增加，Q明显增强。同时，这种切割作用对叶轮内的轴向漩涡结构产生影响，使得轴向漩涡增强，但漩涡范围出现了明显的减小趋势。

图15 叶轮中截面速度分布Fig.15 Velocity distribution of different sections of impeller

图16 叶轮不同截面涡结构分布Fig.16 Vortex structure distribution of different sections of impeller

湍流是自然中存在的极为复杂的流体流动现象，具有多尺度和非定常的鲜明特性。湍动能作为表征湍流强度的参数，具有能量高和传递快等特点。叶轮中截面湍动能分布见图17。从图17可以看出：一方面在射流孔出流区，湍流强度增加，使得叶轮内损失增加；另一方面，叶轮内空泡体积分数明显减小且射流使得空化泡更加稳定，叶轮出口的湍动能明显下降，非定常性引起的湍流脉动减弱。在此工况下，射流孔出口区域干扰作用造成的损失较小，而空化尾部湍动能下降明显，因此，在此工况下，叶轮内损失减小，泵性能得到提升。