连铸结晶器的双源复合激振原理及振动同步控制模型
2021-06-21刘大伟李明明吕晨
刘大伟,李明明,吕晨
(燕山大学机械工程学院,河北秦皇岛,066004)
连铸机结晶器是一个带有活底的水冷铜模,作为高温钢水凝固成型的反应器,它被喻为连铸机的“心脏”。为防止铸坯的初生坯壳与结晶器铜板发生黏结而导致漏钢,结晶器必须按特定规律进行高频小振幅振动[1]。因此,研制具有高可靠性、高承载能力和振动参数智能可调的连铸结晶器激振设备,对发展高效、智能连铸具有重要的意义。研究和实践表明,非正弦速度规律是最适合高效连铸的结晶器振动方式。目前,非正弦激振设备按激振原理可分为液压式、机械式和电动式3类。国内外普遍使用液压式激振器,这类激振器通过伺服阀控制液压缸,进而驱动结晶器振动,可以方便地调整振幅、频率和偏斜率[2-5],但其投资、运行和维护成本较高,存在液压缸漏油和伺服阀零飘的缺陷[6]。机械式激振器采用变频电机作为原动机,通过机械结构实现非正弦振动,如双偏心迭加非正弦振动发生装置[7],应用2 个偏心轮的运动波形叠加,构成了非正弦振动波形,但叠加后形成的非正弦波特性较差,LIU等[8-9]先后开发出以椭圆齿轮副或蜗线齿轮副等非圆齿轮为核心传动元件的非正弦激振器,通过非圆齿轮使偏心轴激振机构实现非正弦振动规律;考虑到非圆齿轮的加工成本,研究人员提出通过逆平行四连杆机构代替椭圆齿轮激振方案[10],机械式激振器以其成本低、控制简单的优势,获得了一定的应用,但存在振幅和波形偏斜率无法在线调整的技术限制。电动式激振器采用伺服电机作为原动机,可实现振动规律的在线控制,相比液压式,具有系统组成简单、运行、维护方便等优势,近年来发展迅速。目前现场使用的电动式激振器根据其机械传动方式分为2类:一类采用丝杠机构,如镭目公司提出的电动缸(由伺服电机和丝杠集成)激振方案,该装置可在线调整所有振动参数[11],但高频振动和长工作时间的运行模式对丝杠精度、抗冲击性及承载能力要求较高;另一类采用偏心轴连杆机构,伺服电机变速驱动偏心轴连杆机构进而带动连铸结晶器非正弦振动[12-13],该系统具有良好的抗冲击性和可靠性[14-15],但其关键振动参数——振幅无法在线调整。
综上所述,目前电动式激振器逐渐成为发展主流,在电动式激振设备中,虽然曲柄连杆机构激振器的力学性能和成本均比丝杠机构激振器的更优,成本更低但无法在线调整振幅的缺陷成为制约其推广和应用的瓶颈,为此,本文提出双源复合激振方式,将2个小功率的伺服电机及偏心轴连杆机构,通过运动合成带动结晶器非正弦振动,在保留偏心轴连杆机构性能优势和不增加电机总功率的基础上,实现结晶器的全部振动参数在线实时调整,并对双源激振器的运行原理以及振动工艺控制进行研究。
1 双源复合激振器的构型
连铸结晶器振动系统主要由激振器、振动台和结晶器组成。结晶器与振动台固定连接,随振动台运动,振动台一端通过串接板簧与机架相连,在板簧的导向作用下,结晶器可以沿预定的弧线或直线轨迹振动。振动台另一端通过弹簧支承,可以对结晶器质量进行平衡。激振器通过连杆或板簧与振动台连接,驱动振动台按给定振动规律运行。
本文提出了一种新型激振装置——双源复合激振器,它由2台伺服电机和1套两自由度连杆机构组成,如图1所示。两自由度连杆机构包含曲柄O1A和O2B,两曲柄等长且回转中心在同一水平位置上,分别与伺服电机连接。另外,2个等长的连杆AC和BE将曲柄的运动传递到横梁CE上,进行运动复合;连杆GC一端与基座铰接,另一端与横梁CE铰接,通过连杆GC小幅摆动,限制横梁CE的运动轨迹;最后2台伺服电机变速运动合成的非正弦振动,在横梁CE的中点处通过连杆DF传递到结晶器振动台。工作时,2台伺服电机分别驱动曲柄做单向的变速旋转运动,在任意时刻曲柄O1A的转角为θ1,曲柄O2B的转角为θ2,2 个曲柄的相位差为φ=θ1-θ2。

图1 双源复合激振器驱动的结晶器非正弦振动系统简图Fig.1 Sketch of non-sinusoidal vibration system of mold driven by double-source composite vibrator
2 双源复合激振器的数学模型及同步控制
2.1 位移及速度模型
由于输出杆的上端直接与结晶器振动台连接,计算输出杆的上端在任意时刻的位移和速度便可知结晶器振动台的位移和速度。结晶器的振动幅值一般为3~5 mm,虽然双源激振器中曲柄长度比振动幅值稍大,但远远小于其他连杆长度,在机构运动中,可以认为点D在竖直方向的运动与结晶器振动规律一致,输出杆下端点D的位置坐标(xD,yD)可根据横梁CE两端点的位置坐标求得:

式中:xC和yC分别为点C的横坐标和纵坐标;xE和yE分别为点E的横坐标和纵坐标。
将图1中双源激振器的两自由度连杆机构拆分成2 个曲柄摇杆机构,左侧曲柄摇杆机构O1ACG如图2所示。图2中,以O1为原点做坐标系O1xy,曲柄O1A的相位角为θ1,摇杆GC与水平方向之间的夹角、AG连线与水平方向之间的夹角、摇杆GC与AG连线之间的夹角分别为α3,β1和β2。曲柄O1A、连杆AC、摇杆GC的长度分别为l1,l2和l3。A和G两铰接点之间的距离lA为

图2 左侧曲柄摇杆机构Fig.2 Crank-rocker mechanism on the left

式中:xA和yA分别为点A的横坐标和纵坐标;xA=l1cosθ1,yA=l1sinθ1,xG和yG为点G的坐标;G的坐标为固定值。
横梁CE的左端点C的坐标为
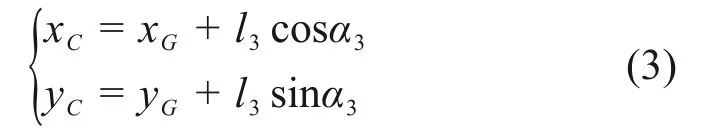
图2中β1和β2分别为

β1和β2恒为锐角,则在任意时刻GC与水平方向之间的夹角为

将α3代入式(3),便可求得C点的位置坐标。
按同样的方法,可求出右侧曲柄摇杆机构O2BEC(图3)中点E的坐标。图3中,以O2为原点做坐标系O2xy,θ2为曲柄O2B的相位角,BC与水平方向之间的夹角、CE与BC之间的夹角、CE与水平方向的夹角分别为β3,β4和α6。曲柄O2B、连杆BE、横梁CE的长度分别为l4,l5和l6,两曲柄回转中心的连线长为l7,BC连线的长度lB为
式 中:xB和yB为B点的坐标,xB=l4cosθ4+l7,yB=l4sinθ4。
横梁CE右端点E的坐标为
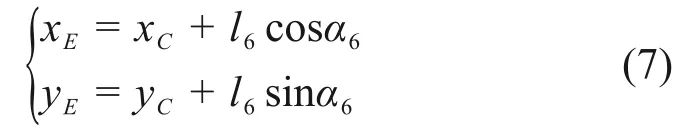
图3中β3与β4分别为
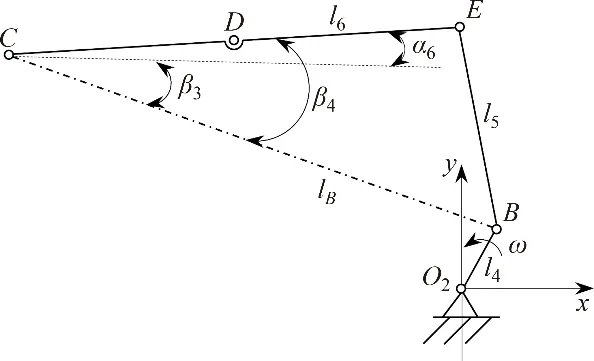
图3 右侧曲柄摇杆机构Fig.3 Crank-rocker mechanism on the right

CE与水平方向的夹角α6为

在求出α6之后,将α6代入式(7),便可求得E点的位置坐标。
将C点和E点坐标代入式(1),便可求得输出杆的下端点D的坐标。进一步对其求关于时间t的导数,可以得到点D的速度vDx和vDy。结晶器的工作方向是竖直方向,因此,结晶器的速度vm=vDy。
2.2 非正弦振动的统一表达式
根据单偏心轴式激振器的运动方程可知[16],要使结晶器产生非正弦振动波形,伺服电机须驱动偏心轴按非匀速周期角速度运转。众多学者提出了种类繁多的非正弦振动波形,如德马克波形、椭圆齿轮波形、蜗线齿轮波形以及分段函数波形,这些波形通常储存在激振器的控制系统中,在生产中由用户选择使用。由于每个波形函数均不相同,这样给控制器的设计和应用带来诸多不便,因此,本文提出基于傅里叶级数的非正弦振动统一公式,不仅有利于设计通用、简便的控制器,而且可以通过傅里叶级数项的选择,有效抑制结晶器振动系统的共振[17]。
双源复合激振器中,两伺服电机以相同的周期规律同步运转,伺服电机的周期速度为

式中:ω0为偏心轴的基频;an和bn为转速波动系数;ij为伺服电机的减速比。
对于图1中的双源复合激振器,伺服电机以式(10)驱动偏心轴运行时,曲柄O1A和曲柄O2B的角位移分别为
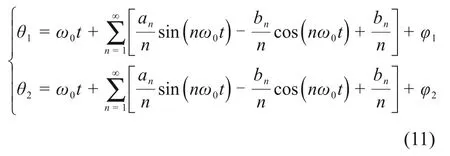
式中:φ1和φ2分别为曲柄O1A和曲柄O2B的初始相位角。两曲柄的初始相位角之差为φ=|φ1-φ2|,其中,φ的取值范围为0~π。
从式(10)和(11)可以看出,双源复合激振系统中的可控参数有ω0,φ和ε。ε=[a1,a2,a3,…,an,b1,b2,b3,…,bn]T,为波动系数。根据需要可以确定不同的项数。将式(10)和(11)代入式(1)即可得到结晶器的非正弦振动波形,从而获得结晶器的3个基本振动参数频率f、振幅h、波形偏斜率α与激振器系统参数ω0,φ和ε之间的关系:

从式(12)可以看出,改变激振系统中的参数ω0,φ和ε即可实现结晶器全部振动参数的在线调控。
2.3 非正弦振动的同步控制模型
根据非正弦振动波形及铸坯的拉速可以求出控制铸坯表面质量的一系列工艺参数,其中比较重要的参数有负滑动时间tN、负滑动超前量NSA和正滑动时间tP。结晶器非正弦振动速度曲线如图4所示,图中,T为结晶器的振动周期,vc为拉坯速度,t1和t2分别为结晶器负滑动开始和结束时刻,则负滑动时间tN为

负滑动超前量NSA等于图4中阴影部分的面积,其表达式为

图4 非正弦波形及工艺参数Fig.4 Non-sinusoidal wave and technological parameters

正滑动时间tP为

浇注过程中拉速随工况的变化而变化,为保证铸坯在不同拉速下均能获得稳定的表面质量,结晶器中的非正弦振动基本参数必须随拉速改变,以确保振动工艺参数的稳定。结晶器振幅、频率和偏斜率随拉速变化的函数关系称为振动同步控制模型,这种同步控制模型比较适用于液压缸激振方式,但对于通过电机带动偏心轴或丝杠的激振系统,还需要将同步控制模型中的频率f、振幅h、波形偏斜率α转化成电机的控制参数,这个过程往往涉及非线性方程的求解,不利于激振系统实现快速、准确控制。
由于本文双源复合激振系统中的3个基本控制参数ω0,φ和ε分别对应结晶器的f,h和α,为简化双源激振系统的同步控制过程并提高控制精度,提出直接建立ω0,φ和ε的同步控制模型代替传统激振系统中f,h和α的同步控制模型,如下式所示:
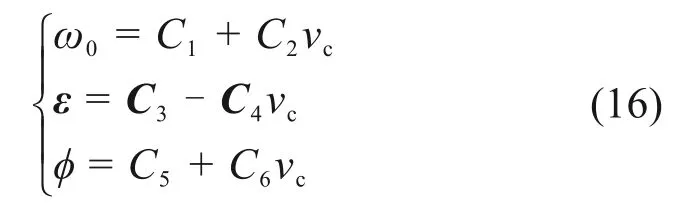
式中:C1,C2,C3,C4,C5和C6均为控制模型的震荡系数。
在实际连铸生产中,可根据钢种和拉速范围,选择式(16)中的1 个或多个函数作为同步控制模型,通常对于拉速变化范围较大的情况,选择多个函数的同步控制模型更容易获得稳定振动工艺。
3 计算结果与分析
将式(10)中三角函数仅取1项,即ε=[a1],可获得经典的德马克波形曲线,以该波形为例进行分析计算。当式(10)中的三角函数取多项时,计算方法相似。
以某钢厂的板坯连铸机为例,其主要工作参数为:拉坯速度vc=1.5~2.5 m/min,结晶器振幅h=2.5~5.0 mm,频率f=0~300 min-1,偏斜率α=0~40%。针对该连铸机设计双源复合激振器的参数为l1=l4=7 mm,l2=l5=400 mm,l3=450 mm,l6=l7=600 mm。2 台双源激振器分别布置在结晶器两侧,同步驱动结晶器非正弦振动,计算得到结晶器振动参数和工艺参数变化规律。
3.1 非正弦振动参数的调控
令ω0=12.6 rad/s,a1=0.33,不同相位差下的位移曲线如图5所示。由图5可知:当φ取π/4,π/3和π/2 时,对应的结晶器振幅分别为6.47,6.06 和4.95 mm,同时,结晶器的振频均为120 min-1,偏斜率均为20%,说明改变两曲柄初始相位角之差能够独立控制结晶器的振幅。当φ取[0,π],其他参数不变时,得到结晶器振幅h随φ的变化规律如图6所示。从图6可见:当相位差φ=0 时,振幅最大,为7 mm,振幅最大值为曲柄长度,故设计曲柄长度时,要保证曲柄的长度不小于结晶器的最大振幅;当相位差φ=π时,结晶器振幅变为0 mm。两曲柄的相位差从0 增大到π,结晶器振幅从曲柄长度l1(l4)下降至0;当相位继续增大到2π时,结晶器振幅从0 再次增大至曲柄长度l1(l4),完成1 个周期,但在实际应用中,φ取值范围为[0,π]。
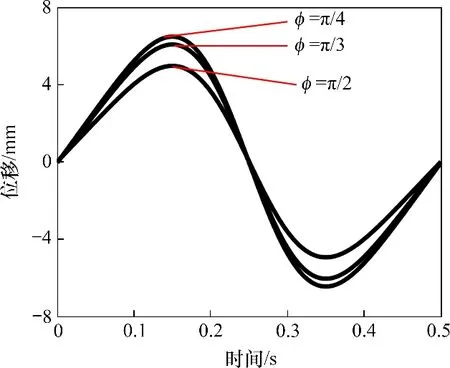
图5 不同相位差下的位移曲线Fig.5 Displacement curves in different phase differences

图6 振幅随相位差的变化曲线Fig.6 Variation of amplitude with phase difference
取φ=π/3,a1=0.33,ω0分别取12.6,14.7,16.8 rad/s时,结晶器的位移曲线如图7所示。由图7可知:结晶器振幅均为6.06 mm,偏斜率均为20%,3条曲线对应的结晶器频率分别为120,140和160 min-1,可见,改变2个电机的频率能够独立地控制结晶器的振频。

图7 不同振动频率下的位移曲线Fig.7 Curves of displacement in different vibration frequencies
取φ=π/3,ω0=12.6 rad/s,a1分别取0.16,0.33和0.53时结晶器的位移曲线如图8所示。由图8可知:相应的结晶器位移波形偏斜率α分别为8%,20%和28%,结晶器的振频均为120 min-1,振幅均为6.062 mm,可见:波动系数ε能够独立控制结晶器位移波形偏斜率。为进一步明确ε对结晶器位移波形偏斜率的影响规律,取ε=[a1],a1∈[0,0.78],其他参数不变,分别计算相应的结晶器位移波形偏斜率,结果如图9所示。从图9可见:当a1=0时,结晶器位移波形偏斜率α为0,此时,结晶器作正弦振动;当a1增大时,结晶器作非正弦振动,随a1增大,α呈近似线性增大。

图8 不同波动系数下的位移曲线Fig.8 Displacement curves in different fluctuation coefficients
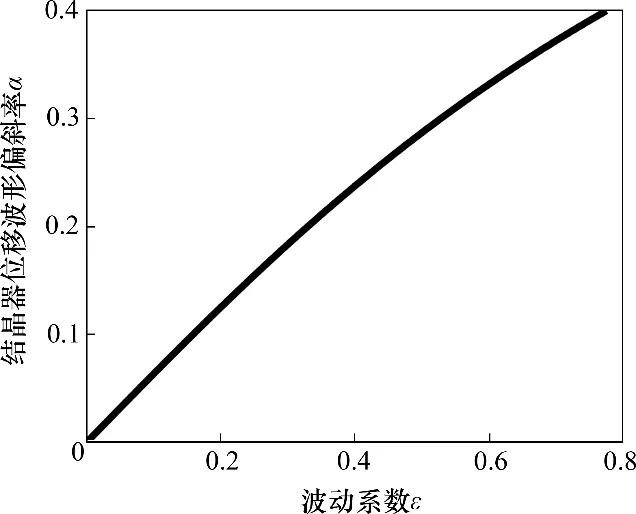
图9 不同波动系数ε下的位移波形偏斜率αFig.9 Modification ratio α of waveform in different fluctuation coefficients
3.2 同步控制模型下的工艺参数
要建立控制模型,必须要明确工艺参数随控制模型的变化规律,基于这些规律对控制模型的参数进行调整,从而达到最佳的工艺效果。经计算得到波形工艺参数随基本参数的变化规律如下:随着波动系数增大,负滑动时间减少,正滑动时间和负滑动超前量增大;随着振幅减小,负滑动时间和负滑动超前量增大,正滑动时间减少;随着频率上升,负滑动时间和正滑动时间均减少,负滑动超前量增大。
该板坯连铸机结晶器采用德马克非正弦波形函数,根据经验取结晶器最优工艺参数范围为:NSA=3~5 mm,tN=0.1 s,tP=0.2~0.4 s。根据波形工艺参数随基本参数的变化规律对控制模型进行调整,得到较理想的控制参数:C1=26.9,C2=4,C3=-0.11,C4=0.2,C5=2.76,C6=0.34。该控制模型下工艺参数随拉坯速度变化曲线如图10所示。从图10可见:在拉坯速度变化范围内,负滑动时间从0.094 s 上升到0.099 s,与理想负滑动时间的误差可忽略不计;其他2个工艺参数也在所设定的范围之内,而且变化范围很小。结果表明:采用基于参数ω0,φ,ε构建的同步控制模型,工艺参数在合理范围内小幅变化,可以保证铸坯在不同拉坯速度下获得稳定的表面质量。
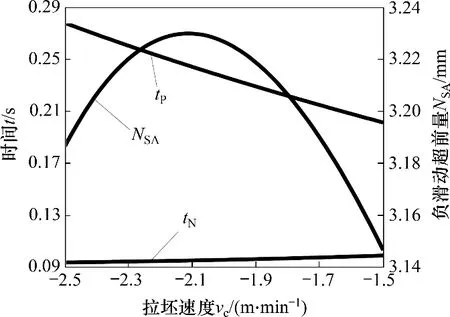
图10 工艺参数随拉坯速度变化曲线Fig.10 Curves of parameters changing with casting speed
4 结论
1)提出一种电动式双源复合激振器,通过2台低功率伺服电机协同配合,可实现连铸结晶器全部振动参数在线调控。由于2台伺服电机都为单向运转,其电机转子产生的惯性扭矩远小于电动缸中高频正反旋转的电机转子产生的惯性扭矩,故双源激振器中伺服电机的功率利用率高,更加适用于重型结晶器。
2)基于傅里叶级数给出了双源复合激振器中伺服电机角速度统一表达式,可通过连续函数构建出结晶器的任意非正弦振动波形,便于结晶器振动参数的智能控制。
3)双源复合激振系统的两偏心轴以一定相位差同步变速运转,偏心轴的角速度基频ω0、角速度波动系数ε和两偏心轴的相位差φ可分别独立控制结晶器的频率f、波形偏斜率α和振幅h;基于参数ω0,φ,ε构建同步控制模型,不仅有利于提升双源激振器控制系统的性能,而且可以保证铸坯在不同拉速下获得稳定的表面质量。
