赛车横向稳定杆的设计研究
2021-06-21刘盛鸿沈丞锴
高 宁,刘盛鸿,沈丞锴
(武汉理工大学汽车工程学院,湖北 武汉430070)
1 引言
中国大学生方程式汽车大赛是一项由高等院校汽车工程或汽车相关专业在校学生组队参加的汽车设计与制造比赛。各参赛车队按照赛事规则和赛车制造标准,在一年的时间内自行设计和制造出一辆在加速、制动、操控性等方面具有优异表现的小型单人座休闲赛车,能够成功完成全部或部分赛事环节的比赛。在设计制造过程中,每支车队需要基于车队拥有的技术和资金协调,设计符合性能需求和成本控制的赛车。
悬架的侧倾角刚度是影响汽车静态侧倾稳定性的主要因素之一,且直接影响到汽车操纵稳定性的其他一些性能指标,如不足转向度、中性转向点侧向加速度等。为加大悬架的倾角刚度,现代汽车大多装有横向稳定杆。
对于横向稳定杆的设计应满足如下要求:①与操纵稳定性直接相关的设计指标是它在车轮处的等效侧倾角刚度,而不是其本身的侧倾角刚度;②稳定杆的设计必须满足强度要求;③应尽量减轻稳定杆的质量[1]。
本文以武汉理工大学电动方程式赛车的悬架为基础,对赛车横向稳定杆的结构进行设计研究。
2 横向稳定杆系统设计
2.1 设计思路
武汉理工大学电动方程式赛车的悬架为经典的不等长双叉臂独立悬架,也是方程式赛车常用悬架形式。
为了满足悬架性能需求,往往需要使用横向稳定杆提供部分侧倾刚度,同时满足侧倾刚度可调的需求。因此,正确地选型、计算、设计横向稳定杆尤为重要。
2.2 横向稳定杆所需提供的刚度并确定布置形式
根据车辆动力学,通过理论计算与Adams软件模拟分析,求得前悬所需侧倾刚度为503 Nm/deg。
由轮胎参数表得,取减震器轮胎中心刚度为37.369 N/m,提供的侧倾刚度为360 Nm/deg,防倾杆提供的侧倾刚度363.9 Nm/deg,总侧倾刚度为504 Nm/deg;同样的方法求得后悬横向稳定杆理想刚度为308.993 Nm/deg。
再通过Adams仿真分析,将悬架的束值、外倾角、横摇刚度等一系列定位参数输入。设定所需的工况,在仿真平台上可以得出该条件下减震器的行程,进而得到连接杆位移,将仿真所得数据与计算结果相结合验证,为实际车辆的制造提供了一定的参考[2]。
横向稳定杆不能提供过多的侧倾刚度。如果横向稳定杆提供过多侧倾刚度,赛车很有可能在过弯时抬起一个车轮。在正常情况下,横向稳定杆给悬架系统提供的侧倾刚度应在50%以下[3]。所以,横向稳定杆刚度可调的设计必不可少。
为配合车身整体布置,避免气流过多影响空气动力学套件效果,2020赛季将前悬横向稳定杆置于车底,后悬横向稳定杆置于车尾顶部包络于整流罩内[4]。前悬横向稳定杆靠近地面,需要仔细做运动校核,避免在跑动过程中发生干涉和蹭地的情况,并限制扭杆在x、y、z轴向的移动。目前国内大部分车队使用的横向稳定杆类型大多为U型或Z型,其中Z型横向稳定杆如图1所示。
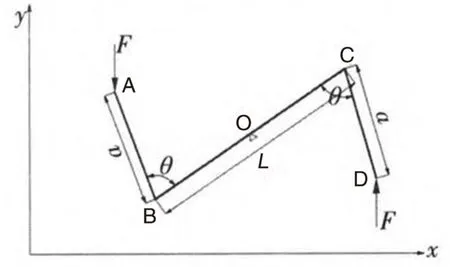
图1 Z型横横向稳定杆理论图
根据Z型横向稳定杆的结构,不难看出,A、D端连接的是左右摇臂,主要受到来自赛车行进时悬架跳动传递的力,从而推动中心杆绕D转动,产生扭转力矩,起到传递左右车轮力矩的作用。而此种横向稳定杆的刚度主要与杆件直径、受力方向、a和L有关;在实际情况中比较难以定量调节,且此种类型的布置形式较为占用空间,考虑到E22的尾部放置有电气设备,因此选用结构简单,方便调节的U型横向稳定杆。
2.3 横向稳定杆刚度转换计算
独立悬架线刚度与侧倾角刚度的转换公式如下:

式(1)中:Kφr为侧倾角刚度,N·m/rad;为侧悬架线刚度,N/m(将横向稳定杆扭杆从中间分开等效成单侧弹簧以便于换算成侧倾角刚度,B为轮距,m。
悬架线刚度公式如下:
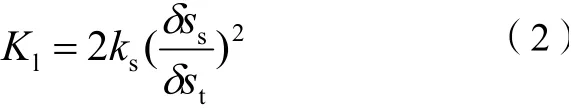
式(2)中:K1为悬架线刚度,N/m;ks为扭杆弹簧近似提供的线刚度,N/m;δss为横向稳定杆臂与横向稳定杆连接杆连接孔的中心的微元位移;δst为轮胎接地点的微元垂直位移。
弹簧线刚度计算公式为:

式(5)中:T为扭杆承受的转矩,N·mm;R为横向稳定杆臂长,mm。
在实际工作状况下,扭杆与端头部分采用螺栓连接,因此,可以将两端的突出部分转换为当量长度;在计算刚度时,扭杆的有效长度是杆体长度加上两端杆端部分的当量长度。


式(8)中:D为横向稳定杆扭杆外径,mm;d为横向稳定杆扭杆内径,mm。
将式(4)(5)(6)(7)(8)代入式(3)中得:
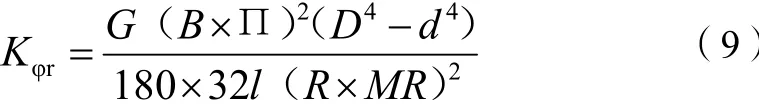
以后悬为例,本次设计中,根据摇臂位置以及2019年后悬横向稳定杆的臂长取了合适的臂长60mm和杆长620 mm,并取一个变化较小点位合适的传动比,最后,通过调整扭杆管径来调节刚度达到理想值。实际计算中,将计算生成excel表格,等式两边情况为:Kφr代表理想横向稳定杆刚度;G来自材料选择,2020赛季选择弹簧钢42CrMo,杨氏模量查表可得;B为轮距为总布置取值;臂长R、杆长L已知,D、d未知,MR有理想值。
定义钢管内外径为自变量,MR为因变量,通过改变管径使MR数值逼近理想值,记录合适的管径组合,验证管径是否满足市面上容易购得、不会和其他部件干涉和强度校核3个要求。
3 横向稳定杆系统的强度校核
校核主要从材料力学的角度出发,扭杆(薄壁杆件)横截面切应力公式如下:

式(10)中:τ为薄管壁平均切应力,MPa;T为杆端所受扭转矩,N·mm;D为扭杆外径,mm;t为扭杆壁厚,mm。
高职中外合作办学是近年来许多高职院校推进高职教育人才培养国际化、多元化发展的一项重要措施,但由于办学模式、人才培养定位模糊等一系列问题的存在,使得我国高职中外合作办学长期存在着“先天不足,后天畸形”的问题。为进一步促进高职院校中外合作办学的良性发展,有必要对当前高职中外合作办学的现状、问题等进行深入分析,进而采取针对性措施。

式(11)中:ks为扭杆弹簧近似提供的线刚度,N/mm;δ为扭杆端最大挠度,mm;R为横向稳定杆臂长,mm。
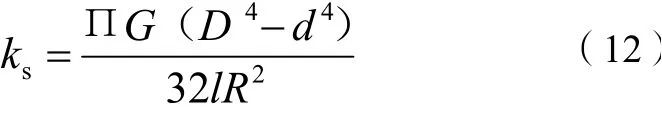
式(12)中:G为剪切弹性模量,MPa;D为横向稳定杆扭杆外径,mm;d为横向稳定杆扭杆内径,mm;l为横向稳定杆长度,mm。
其中,最大挠度可近似为由Adams的仿真获得最大轮跳时横向稳定杆连接杆在摇臂上孔的位移。
4 重要零件的设计与校核
4.1 零件设计与分析思路
由于横向稳定杆的扭杆在侧倾过程中会发生较大的形变,会改变横向稳定杆端部零件和扭杆的受力工况,所以单独分析一个零件不足够准确,校核扭杆剪切力也只能作为初步的校核。在分析过程中,应该将其带入到实际的工作状态下与其他构件整体进行分析。
在本次设计研究中,使用圆柱体代替螺栓以减小分析求解的计算量,并设置合适的接触类型,在保证结果可信的情况下最大限度简化工况。为了减小计算量,划分网格时加密容易出现应力集中的部位,并保证每个面有三层网格以上来达到计算准确度。
在这种条件下,能够最大限度地还原零件受力的真实情况,避免在跑动过程中发生意外。由于横向稳定杆结构较为简单,且在实际跑动过程中受力情况单一且数值较小,因此,在零件设计校核过程中,最低安全系数设置为2。
4.2 前悬横向稳定杆设计
以前悬横向稳定杆扭杆为圆心,前悬横向稳定杆连接杆的杆端连接点为切点,设置三档,通过改变力臂实现刚度的调节。同时,为降低加工成本,将力臂中间部分做成平面。由于扭杆位置与摇臂孔位有一定高度差,因此杆端设计可以较为规整,再参照所用标准件尺寸,完成前悬横向稳定杆设计。主要查看两个主要设计件的结果。
由计算可得,装配体在给定受力状况下,前悬横向稳定杆杆端最大应力为114 MPa。与预测相同,最大应力出现在杆端连接孔处。查阅资料可知杆端材料7075-T6的屈服强度为505 MPa,经过计算得出,零件的安全系数为4.43。前悬横向稳定杆杆端应力如图2所示。

图2 前悬横向稳定杆杆端应力云图
与预测相同,最大应力出现在扭杆的孔位处,为380 MPa。查阅资料可知,42CrMo的屈服强度为930 MPa。安全系数为2.44,均满足所设定的要求。前悬横向稳定杆扭杆应力如图3所示。

图3 前悬横向稳定杆扭杆应力云图
4.3 后悬横向稳定杆设计
后悬的布置相比于前悬更加紧凑,由于结构限制需要将力臂设计成弧形。以后横向稳定杆连接杆的摇臂连接点为圆心,后横向稳定杆连接杆的杆端连接点为切点,设置三档,通过改变力臂实现刚度的调节,实际获得力臂为圆弧半径。将零件装配完成后带入Ansys Workbench静力分析模块中进行受力分析,接触类型、网格划分、约束条件与前悬类似,不过多赘述。
分析得到装配体的应力分布情况结果收敛到10%以下,如图4所示,结果可信。
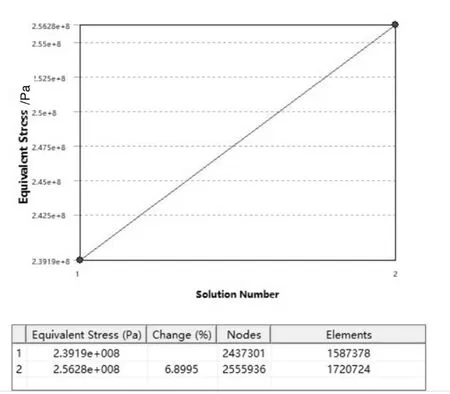
图4 后悬横向稳定杆仿真收敛情况
装配体在给定受力状况下,后悬横向稳定杆杆端最大应力为85 MPa,出现在端头连接孔处。经过计算得出,零件的安全系数为5.94。后悬横向稳定杆扭杆最大应力出现在孔位处,最大应力为256 MPa,安全系数为3.63。均满足设计要求。
5 总结
通过计算和三维建模以及静力学仿真,完成了赛车横向稳定杆的设计。该设计符合赛车对于侧倾刚度的需求,也在成本允许的范围内尽可能优化设计,达到轻量化目标。计算及校核的流程可以延续使用在未来的赛车上。若未来继续使用传统双叉臂独立悬架配合U型横稳,应改进调节刚度的方式以及考虑更多材料。
