基于邻域决策的序贯三支分类方法
2021-06-21王文剑
亓 慧 魏 巍 王文剑,3
1(太原师范学院计算机系 山西 晋中 030619)2(山西大学计算机与信息技术学院 山西 太原 030006)3(山西大学计算智能与中文信息处理教育部重点实验室 山西 太原 030006)
0 引 言
三支决策理论的原生模型为粗糙集和决策粗糙集,该理论的衍生与拓展实则为粗糙集理论中三个区域提供了恰当的语义解释[1-2]。其核心思想是将一个统一集划分为三个互不相交的不同区域,进而对每一个区域采取相应的决策策略[3]。例如,在粗糙集理论研究中,通过下近似集合与上近似集合的定义,论域可被划分为正域、负域、边界域。作为传统二支决策理论的一种重要推广,三支决策理论给决策者分别分配接受、拒绝、不承诺决策。而在面向实际问题的决策过程中,人们最初面对的信息往往是不确定的,不足以完成确切的决策,而是需要另外一个待定渐进的过程来进行新的有效信息的补给。因此,在真实环境中,伴随着信息的迭代补充,决策过程以及决策结果也应更新与递进。事实上,我们就将这种从粗粒度到细粒度的决策过程称之为序贯决策方法[4]。
在原有三支决策研究成果的基础上,Yao等[4-5]于2003年开创性地构建了序贯三支决策的研究理念,并进一步地给出了一种具体的序贯三支决策算法。在此思想的引导下,众多研究工作者从不同方面针对序贯三支决策思想开展了大量的工作。Li等[6-7]提出了代价敏感的序贯三支决策方法;Qian等[8-9]在动态粒度方法下研究了基于序贯三支决策的属性约简方法;Li等[10-12]探索了图像等非结构化数据中的序贯三支决策模型,用以平衡决策过程中的决策代价和时间代价,并将序贯三支决策与自编码网络相结合,寻找总代价最低的合适粒度。Yang等[13-16]系统研究了概率粗糙集下序贯三支决策的框架;Yang等[17]基于粗糙集方法研究了代价敏感序贯三支决策的最优粒度选择问题。此外,三支决策和序贯三支决策在分类问题中也发挥着独特的作用。Zhang等[18]研究了基于分类错误的三支决策模型;Yao等[19]提出了三支决策分类的基本框架;Yue等[20]基于模糊覆盖粗糙集构建三支分类技术。在序贯三支分类的研究过程中,如何界定属性集序列是序贯分类的重要问题之一。在已有的研究成果中,大多建立在前向式框架上,即以第一个属性为起始序列,以全部属性集为终止序列[13]。然而,在高维数据背景下,数据中存在大量的冗余属性,现有的属性序列非常耗时且低效。针对这一问题,Ju等[21-22]首先借鉴局部约简的思想,将局部约简设置为属性序列的起始集,将全局约简设置为属性序列的终止集。进一步地,Ju等基于合理粒度准则,提出了一种新颖的多粒度分类预测方法。
另一方面,经典粗糙集模型由于其不可分辨关系的特殊性,仅能处理离散型数据,尚不能有效处理连续型数据甚至混合复杂数据。鉴于此,Lin[23]建设性地将邻域拓扑的思想引入于粗糙集,设计出了邻域粗糙集的最初模型。Hu等[24-25]从粒计算的角度重新阐释且设计了邻域粗糙集模型,取得了丰富的研究成果。在邻域粗糙集理论中,其相应的决策错误率是一个重要的概念[26]。邻域决策错误率为从分类学习的视角研究属性子空间的提取问题提供了一种新的度量标准。由邻域决策错误率约简构建而来的属性子空间可以获得较为理想的邻域决策错误率[27]。
邻域决策错误率为序贯三支分类问题中局部和全局属性子空间的设定提供了一种新颖的思路。基于以上讨论,本文系统研究了基于邻域决策的序贯三支分类方法。首先,通过基于邻域决策错误率的属性约简方法构建序贯三支分类问题中的局部属性子空间和全局属性子空间。基于此,可获取邻域粗糙集在两种不同属性子空间下的正域、负域和边界域,用于后续的预测工作。在预测阶段,若样本不能在当前属性子空间中得到明确分类则需要在更细的属性子空间进行判断,并更新相应的三域信息和邻域信息,以实现不同样本能够在合适的属性子空间上进行分类。
1 序贯三支决策与邻域粗糙集
事实上,首先将给定对象分为三个独立的分支,进而对不同分支分别采取不同的应对措施是三支决策的核心机制,该举措也为认知与决策任务提供了一种分层递进的信息处理范式。需要注意的是,本文引入实体函数和阈值来获取三支决策中三个独立的区域。令U为论域,对于论域中的任意对象x∈U,令E表示评价函数,其中E(x)表示对象x的决策状态值。借助阈值α和β,可将正域、边界域和负域形式化地表示为:
POS(E)={x∈U:E(x)≥α}
(1)
NEG(E)={x∈U:E(x)≤β}
(2)
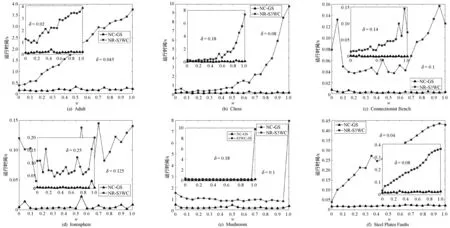
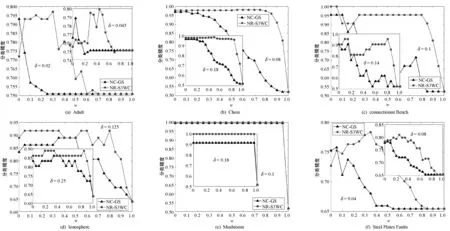
BND(E)={x∈U:β (3) 纵观现有关于粗糙集和三支决策的研究工作,其讨论核心大多围绕非动态的决策系统或数据描述。但是,在面向真实场景的决策问题中,人们最初收集到的信息往往是不确定的,此外,伴随着信息的迭代补充,决策过程以及决策结果也应更新与递进。令DesAk(x)表示信息粒Ak对于对象x给出的刻画,若给定n个不同粒度,则可知对象x在这些粒度上的n个刻画与描述,记为: DesA1(x)DesA2(x)DesAk(x)DesAn(x) (4) 在粗糙集理论中,数据集往往被描述为一个二元组,称作决策信息系统,一般被形式化地刻画为S= 对于∀a∈AT∪D,定义映射:U→Va,Va表示属性a的值域,即a(x)∈Va(∀x∈U)。 定义1令S为一决策系统,对于∀xi∈U,B⊆AT,对象xi基于属性子空间B的邻域则可定义为: δB(xi)={xj|xj∈U,ΔB(xi,xj)≤δ} (5) 式中:ΔB为利用属性子空间B上的信息计算对象xi与xj之间的距离函数。距离函数需满足以下条件: (1)ΔB(xi,xj)≥0。 (2)ΔB(xi,xj)=0当且仅当xi=xj。 (3)ΔB(xi,xj)=ΔB(xj,xi)。 (4)ΔB(xi,xk)≤ΔB(xi,xj)+ΔB(xj,xk)。 在本文中,运用了高斯核距离。对于任意的对象xi和xj,高斯核数可定义为: (6) 式中:σ为给定的参数。进一步地,可将距离函数定义为: (7) 根据径向基函数核距离,可得任意两两对象之间的距离如下: (8) 基于径向基函数核距离函数可定义邻域粗糙集如下。 定义2令S为一决策系统,对于∀X⊆U,B⊆AT,对象xi基于属性子空间B的邻域表示为δB(xi),上、下近似集就可分别被定义为: (9) (10) 在邻域粗糙集模型中,根据决策属性D的信息可将论域划分为{X1,X2,…,Xl},则近似质量可表示为: (11) 在粗糙集属性约简方法中,近似质量经常作为度量属性分类能力的重要指标之一。Hu等[26]认为样本落入粗糙集边界域中并不表示其一定会被错分,只有边界域中的少数类样本存在被错分的可能。为此Hu等基于邻域粗糙集模型,从样本错误分类角度提出了邻域决策错误率,并将其作为提取属性子空间的指标[26]。 假设δB(xi)为样本xi的邻域,P(ωj|δB(xi))(j=1,2,…,c)为δB(xi)在类别ωj下的类别概率。根据此概率可预测样本xi的对应标记。若P(ωl|δB(xi))=maxjP(ωj|δB(xi)),则样本xi的类别标记为ωl,表示为ND(xi)=ωl。显然,ND(xi)=ω(xi)表示对于样本xi而言,其预测标记与真实标记无差。基于此,Hu等给出样本误分类的损失函数如下: (12) 由此可得邻域错误率如下: (13) 式中:n表示样本数。 利用邻域决策错误率,众多学者[28-31]探索了基于邻域决策错误率的属性约简准则,其定义如下。 定义3令S为一决策信息系统,对于∀A⊆AT,A为决策信息系统的一个邻域决策错误率约简,当且仅当: (1)NDERA≤NDERAT。 (2) 对于任意的A′⊂A,都有NDERA′>NDERA。 如定义3的约简集合不仅能够删除决策信息系统中的冗余属性,而且能够使得原决策系统的邻域决策错误率尽可能地降低。因此,本文将其定义为序贯三支分类框架中的全局属性子空间。 在序贯三支分类架构中,局部属性子空间是全局属性子空间的真子集。为此,可从全局属性子空间中截取一部分属性子集作为局部属性子空间,且该截取子集也应尽可能地降低邻域决策错误率,其形式化定义如下。 由定义4可知,基于局部属性子空间的决策信息系统不仅邻域决策错误率相较于原始决策信息系统已降低了至少一半以上,而且压缩了原决策信息系统的属性规模。从序贯三支分类角度看,局部属性子空间也降低了其属性搜索规模。 根据邻域决策错误率约简的定义,对于任意的B⊆AT,a∈AT-B,属性a相对于属性子集B的重要度为: SIG(a,B,D)=NDERB-NDERB∪{a} (14) 根据属性重要度,可设计全局和局部属性子空间求解算法如算法1所示。 算法1基于邻域决策错误率的全局和局部属性子空间 输入:邻域决策系统S= 输出:全局和局部属性子空间BG和BL。 1. ∅→BG,∅→BL; 2. Do 3. ∀ai∈AT-BG,计算重要度SIG(ai,BG,D); 4. 选取最大的重要度及对应的属性aj; 5. IfSIG(aj,B,D)>0 then BG=BG∪{ai}; End If 6. 计算NDERBG; 7. UntilNDERBG≤NDERAT 8. Fori=1:|BG| 9.BL=BL∪{ai}; 11. Break; 12. End If 13. End For 14. 返回BG和BL 基于以上讨论,本文以局部属性子空间为起始序列,以全局属性子空间为终止序列设计一个如算法2所示的序贯三支分类器。 算法2基于邻域决策错误率的序贯三支分类算法 输入:邻域决策系统S= 输出:测试样本s的标记。 1. 根据算法1求得BG和BL; 2. 计算M=BG-BL,得到M={a1,a2,…,al}; 3. 令X=argmaxXj{|Xj|},其中Xj={x∈U:ω(x)=ωj}; 9.i=1; 10. Whilei≤|M| 11. Ifδ(x)⊆POS,then 12. 分配测试样本s正标签;break; 13. Else ifδ(x)⊆NEG,then 14. 分配测试样本s负标签;break; 15. Else 16.BL=BL∪{ai}; 21. End if 22.i=i+1; 23. End if 24. End While 25. If 测试样本x未分配标记 26. 根据δ(x)中多数对象的标记分配给x; 27. End if 28. 测试样本x的标记 本文将所提算法命名为基于邻域决策错误率的序贯三支分类算法,并简写为NR-S3WC。NR-S3WC主要分为5个环节:(1) 根据局部属性子空间信息,进行初始化运算;(2) 分析测试样本与训练样本两两之间的高斯核距离度量值;(3) 求得测试样本的邻域信息粒;(4) 观测当前属性子空间下邻域信息粒中训练样本的标记,进而给出待预测标记;(5) 如若1至4环节过程未能得出确切的标记信息,则根据全局属性子空间下的信息粒,由多数投票原则预测测试样本的标记。 在邻域类分类器中,邻域阈值的确定也是关键之一。本文借鉴Hu等提出方法,根据式(15)设置邻域。 (15) 为了验证所提NR-S3WC分类方法的有效性,本节在6组公共UCI数据集上进行了一系列相关的对比实验,其具体信息如表1所示。本节所用数据均下载于UCI公共数据库,且都为完备数据。此外,本文还采用10折交叉验证方法,将原始数据集随机划分为互不相交的训练集与测试集。其中:训练集用以构建NR-S3WC分类模型;测试集则用以评估分类预测的准确性。 表1 数据描述 为了验证本文方法的有效性,图1至图3分别从属性个数、运行时间和分类精度角度对比了本文方法和Hu等提出的邻域分类方法[32]。 图1 属性个数比较 图2 运行时间比较 图3 分类精度比较 考察图中的实验结果,可得到如下结论: (1) 从属性个数角度不难看出,随着阈值w的不断增大,NR-S3WC算法所需要的属性个数不断增大。这意味着当算法选择相对较高的w值,那么其需要的属性数则越多。此外,当w值越接近于1时,NR-S3WC算法所需要的属性数也越接近于全局属性子空间的属性个数。 (2) 从算法运行时间来看,Hu等提出的邻域分类方法优于本文方法。这是由于算法不同运行机制导致的。众所周知,Hu等提出的邻域分类方法是基于某一特定的属性子空间,本文算法基于邻域错误率约简属性子集,并在分类中作出一次性决断。而NR-S3WC算法则是基于序贯三支分类思想,针对每个测试样本,均需寻找其最合适的属性子空间,故需耗费更多的时间。 (3) 从分类精度结果来看,不难得出本文方法在多数w值下,分类精度优于邻域分类方法。有趣的是,当阈值w取两端极值时即w=0或w=1时,两种算法的分类效果均一般。 综上所述,相较于Hu等提出的邻域分类方法,本文方法虽需耗费更多的运行时间,但在相对较少属性的条件下能够获取更高的分类精度,提高了数据的分类性能,是一种有效的分类方法。 为了进一步丰富和发展序贯三支分类方法的研究,本文引入邻域决策错误率约简构建序贯三支框架中的全局属性子空间,并基于此提出合理的局部属性子空间。基于局部和全局属性子空间,提出一种基于邻域决策错误率的序贯三支分类算法。公共数据集上的对比实验表明,该方法虽消耗了更多的运行时间,但能够在相对较少属性的条件下获取更高的分类精度,提高了数据的分类性能,故本文方法是一种有效的分类方法。
2 基于邻域决策错误率的序贯三支分类
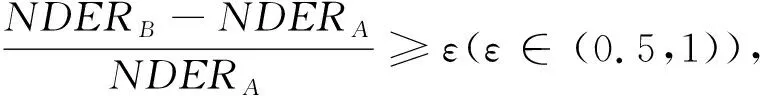

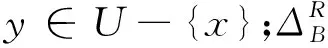
3 结果分析


4 结 语
