监控视频中运动模糊车牌图像参数估计和复原

徐浩森

（中国刑事警察学院，辽宁 沈阳 110854）

关键字：运动模糊；Radon 变换；直方图均衡化；Lucy-Richardson 算法

随着“天网工程”等各类治安防控视频监控系统的建设，视频侦查已广泛应用于各警种工作中，为事前预警、事中防控和事后侦查等技术的重要支撑。但监控系统不可避免地受到诸多因素的干扰，如光学系统衍射、光学系统的相差、聚焦不实、相对运动等，这些因素都会造成图像退化[1]。其中因相对运动而产生的模糊是监控视频中常见的问题之一，尤其是视频中的车辆牌照很容易产生运动模糊，使侦查人员不能及时获取有效的车辆信息，影响案件的侦办时效。因此，需要对运动模糊车牌图像进行复原，进而从中得到有效的车辆信息。

在运动模糊的车牌图像处理中，复原运动模糊图像的关键是需要通过一些先验知识计算出原始图像退化时所形成的点扩散函数（PSF）。因此，深入研究对PSF 参数的精确估记具有重要价值。对于运动模糊图像的模糊参数估计，当前国内外学者已研究出各类方法并取得了一定的成效。其中，一些学者发现模糊图像频谱图中的明暗条纹具有某种分布规律，并针对这种规律提出了对应的参数估计方法，如Radon 变换、RANSAC 变换等[2]。文献[3] 通过对频谱图进行二次变换后使用Radon 变换估计模糊方向，并应用改进的路西理查德森算法复原图像，但无法避免十字亮纹的影响。文献[4]提出先对模糊图片进行分块，选择信息丰富的部分使用Radon 变换检测角度，提高了检测精度，但在像素占比过小的模糊图像中，不易于在频谱中呈现出特征。文献[5] 提出频谱图分块结合边缘检测的方法，避免了十字亮纹产生的影响。文献[6]为提高噪声存在时检测结果的鲁棒性，提出使用加Hamming 窗的改进算法。文献[7]利用频谱分块和结合灰度均值进行反色处理来评估模糊角度，但无法避免实际模糊运动图像中十字亮纹的影响。

在单帧监控视频模糊车牌图像处理中，消除十字亮纹的影响后结合Radon 变换更具实用性。因此，针对运动模糊图像频谱中出现的十字亮纹现象，对频谱图进行直方图均衡化等操作来提高其对比度和消除十字亮纹后进行Radon 变换，从而提高了对于监控视频中运动模糊车牌图像PSF 参数估计的精确性。

一、运动模糊图像模型及其频谱特性

获取图像时，因监控探头与车辆之间可能会产生相对运动，经常会造成图像车牌部位的模糊。但由于监控曝光时间很短，且车辆的运动速度较快，因此，可以大致看作是匀速直线运动。因此，一般情况下，研究匀速直线运动所造成的模糊图像的恢复问题在处理监控中车牌模糊图像更具有应用价值和普遍意义。

（一）运动模糊图像模型

成像时具有相对运动的图像退化模型如图1 所示，由于匀速运动退化后的图像可表示为

图1 图像的退化过程

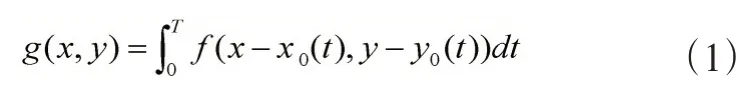
其中，g(x,y)为模糊图像，x0(t)、y0(t)分别为图像f(x,y)在x和y方向上的变量，为运动时间。

对运动模糊图像退化模型进行傅里叶变换可得

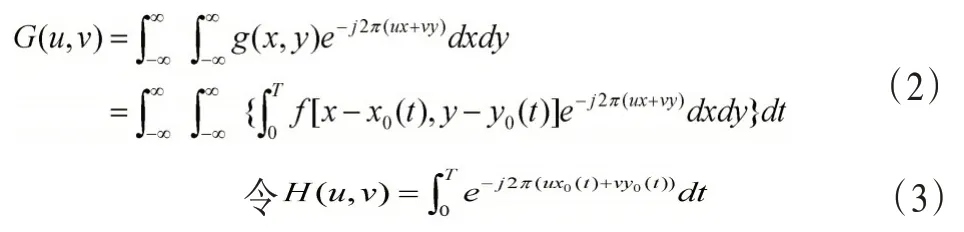
根据傅里叶变换的性质，对上式进一步推导可得

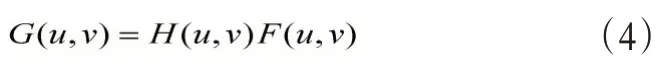
由此可知，若已知函数xo(t)和y0(t)的性质，则可以恢复原图像f(x,y)。

（二）运动模糊图像的频谱特性

将模糊角度θ、模糊长度为d个像素的运动模糊图像的PSF 设为

考虑f(x,y)为离散M×N矩阵，则模糊核的频谱可以表示为[8]

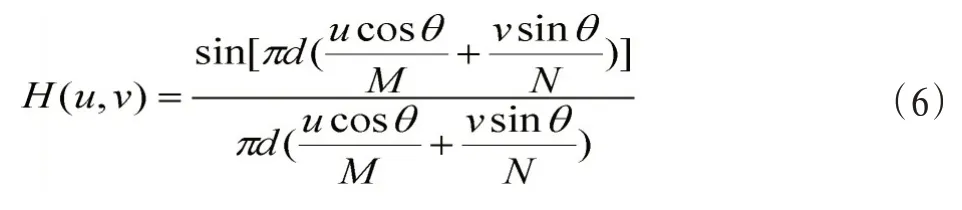
由式（5）可知模糊核的频谱为一个函数，且存在周期性零点，在频谱图上呈现出周期性的暗条纹如图2。因此，识别它们的间隔和方向，就能确定d和θ，从而能够确定模糊核函数。

图2 运动模糊图像频谱图

二、运动模糊参数估计

（一）Radon 变换检测图像直线

Radon 变换和Hough 变换类似，都是用于检测图像中的直线。其原理是，将原来的函数通过一定的空间转换，即在A 平面内的点映射到B 平面上，故原来在A 平面上的一条直线全部的点都落在B 平面的相同一点上。对于函数f(x,y)，它在给定的坐标系XOY中，沿着某投影方向，对其每一条投影线计算f(x,y)的线积分，就得到该射线上的投影值g(R,θ)，其数学表达式如下[9]：

对运动模糊频谱图进行Radon 变换，角度从0°到179°每隔1°做Radon 变换。通过Radon 变换后结果的最大值即为原图像中最明显的直线，即运动模糊的角度。此外，还可以获取Radon 变换结果中其他较大的值，对应图像中的其他直线。

（二）运动模糊车牌图像的频谱图中心十字亮纹形成原因

对于真实的运动模糊图像来说，由于模糊过程的复杂性，其频谱上的暗条纹并不一定清晰。假设模糊核h(x,y)与原始图像f(x,y)是完全卷积的，则所产生的运动模糊图像g(x,y)的尺寸应比f(x,y)大。由参考文献[10]可知，当对一张清晰的图像沿与x轴正向成θ角的运动角度且运动距离为d时，退化所产生的运动模糊图像的宽和高应分别比清晰图像增加d cosθ和d sinθ。但在实际中因监控探头的成像空间不发生改变，实际产生的模糊图像相较软件生成的模糊图像在边缘四周必然存在一定的损失。事实上，正是因为倾斜角度过大的边缘截断损坏了模糊图像边缘附近的卷积关系，使得退化过程不是一个完全卷积的关系，最后导致模糊图像频谱经过中心化后中间出现了十字形的亮纹[7]如图3 所示。

图3 实际运动模糊图像频谱图

因此，在单帧监控视频模糊车牌图像的频谱中，其中间部位存在较明显的十字亮纹，这就给模糊核参数识别造成较大的困难。故在对单帧监控视频模糊车牌图像进行模糊参数估计时，消除中心十字亮纹和提高明暗纹清晰度是最为关键步骤。

（三）基于Radon 变换前消除十字亮纹的角度估计

Radon 变换虽然能实现对PSF 参数的估计，但是发现该算法遇到某类图像时，估计出来的参数值误差不小或者无法估计，这类图像有一个共同的特点就是频谱图中间存在明显的十字亮纹，从而导致无法进行角度估计。对于此类图像，我们需要利用相关手段来减小十字亮纹对运动角度估计的影响。

在单帧监控视频模糊车牌图像中，由于我们的用途是为了获取车牌信息，故可以将图像进行裁剪只保留车牌部位以增强运动模糊图像特征在频谱图中的反映。由图4(a)及其直方图4(b)可知，频谱图中明暗条纹对比度低，不利于Radon 变换检测角度。因此，需要使用直方图均衡化以提升频谱图中明暗条纹的对比度。由上文可知，多数运动模糊图像的频谱图中间存在明显的十字亮条纹，在提升对比度的同时也将十字亮条纹变得更加明显，极大干扰了Radon 检测的效果，如图5(a)所示。因此，为了避开十字亮纹对检测的干扰，可利用画笔工具人为将十字亮条纹涂黑，从而消除其对模糊角度估计的影响。将处理后的频谱图进行Radon 变换，如图5(b)所示，图6 为检测结果，可见经过处理后的频谱图能够有效的提取暗条纹信息，使角度检测结果更加准确。

图4 未处理的模糊图像频谱图及直方图

图5 直方图均衡化及画笔增强后的频谱图

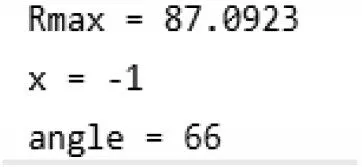
图6 MATLAB 进行Radon 变换估计角度结果

（四）运动模糊长度估计

通过实验观察发现，当改变图像的模糊角度时，其频谱图中的暗条纹与水平轴正向的倾斜角度也紧随其产生变化。设暗条纹与X 轴的正向倾斜角度为φ，也就是直线（)=0斜率所对应的角度，即tan(φ)=-变换可得

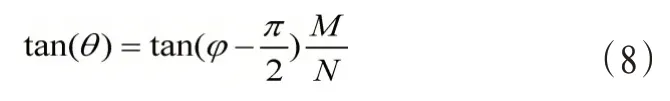
通过公式（8）可知，当已知模糊角度θ时，将运动模糊图像的频谱图沿反向旋转θ°，使得暗条纹与水平方向垂直，即模糊角度为0°。对H(u)=0求解即可得出模糊长度[11]，模糊长度d和模糊图像频谱图中暗条纹间距l之间的关系是

因此，只要确定暗条纹间的距离即可根据式（9）确定图像的模糊长度。具体步骤为：将反向旋转θ后频谱图向u投影求和，利用整列统计信息增强减少随机性干扰，得出其曲线图如图7。通过求解中心最大值两边第K个极小值之间的距离，即为两条暗条纹间距的2k 倍，再由公式（9）得出图像的模糊长度[5]。

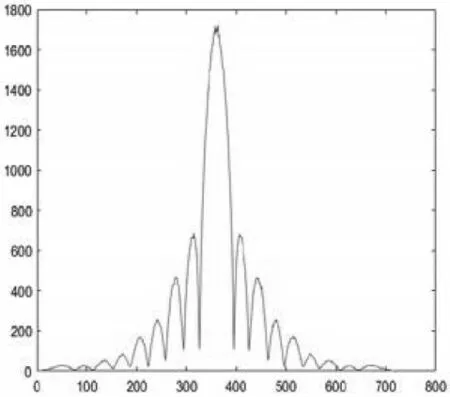
图7 频谱图按列求和曲线图

三、模糊车牌图像的复原及分析

选取四张不同像素值的运动模糊图像，在MATLAB（R2019b）和警视通V5.0.0.0official version private build（20180420）环境下，使用相关方法分别对四幅图像进行复原处理。

（一）模糊参数检测结果

实验图像选用图8 所示的188×187 的监控图像。使用MATLAB 对其进行模糊角度为0～180°（每20°取一个角度），模糊距离l为10 的运动模糊实验仿真，检测结果如表1 所示。

表1 运动模糊车牌图像角度估计结果（单位°）

图8 监控视频截图

其中“直接”表示直接对频谱图进行Radon 变换进行角度检测；“警视通”表示使用警视通自动去运动模糊进行角度检测；“消除亮纹”表示对频谱图进行直方图均衡化并结合画笔工具消除十字亮纹后使用Radon 变换进行角度检测。

检测结果表明，直接对单帧监控视频模糊车牌图像的频谱图进行Radon 变换时，由于运动模糊车牌图像频谱图中十字亮纹的干扰，使检测结果严重偏离实际角度；使用警视通自动去运动模糊进行角度检测只有在模糊角度为0°时检测出准确的角度；而采用对频谱图进行直方图均衡化并结合画笔工具的方法，避开了十字亮线的影响，同时极大地减少了角度检测误差，可以满足高精度估计参数的要求。

（二）不同像素值的模糊车牌图像复原及分析

对频谱图进行直方图均衡化并结合画笔工具消除十字亮纹后使用Radon 变换进行角度检测。为验证该方法的效果，使用MATLAB 中的Lucy-Richardson 算法对选取的四张在监控视频占不同像素的模糊车牌图像进行复原。

图9 为较高车牌像素值占比的图像复原结果，MATLAB 盲复原不能复原出车牌信息，而精确估计参数后可以清楚的复原出模糊图像中的车牌信息以及较轻的振铃效应。当车牌像素值占比减少时，复原结果如图10 所示。

图9 128×60 像素值复原结果

图10 103×46 像素值复原结果

由图10 可见，在车牌像数值占比减少时，MATLAB盲复原依然不能复原出车牌信息，而精确估计参数后可以清晰的复原出车牌中的数字信息，但振铃效应较图9 加重。当车牌像素值占比继续减少时，复原结果如图11所示。

图11 98×39 像素值复原结果

由图11 可见，对模糊图像复原仍能识别出部分车牌信息，但振铃效应较为严重。当车牌像素值占比减少为79×38 时，结果如图12 所示。

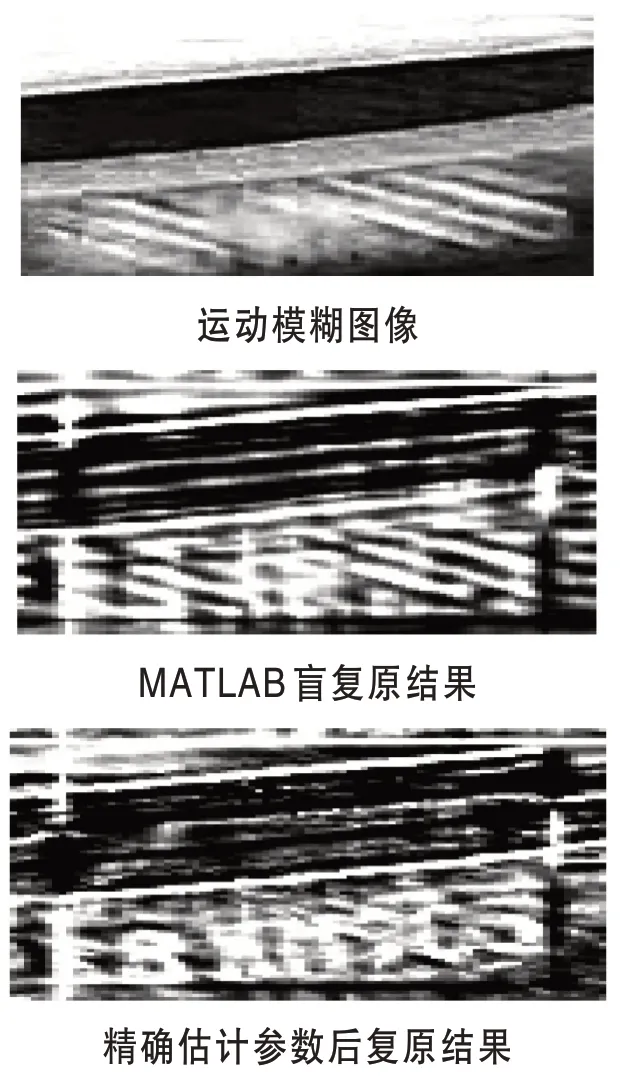
图12 79×38 像素值复原结果

可见，在车牌像素值不断减少时，通过精确估计模糊参数，依然能够识别出模糊图像的部分车牌信息。

通过这四组不同像素值模糊图像复原结果可以看出，消除十字亮纹后进行Radon 变换的方法在求模糊图像的角度与长度的问题上都要比未知参数的情况下进行盲复原的效果更加明显。同时，在实验中发现，在复原后简单地去除噪声，可以使图像的视觉效果更加清晰。

对复原图像进行分析后发现，单帧监控视频模糊车牌图像中往往存在严重噪声或车牌像素过低，造成频谱图特征不清晰、亮暗条纹对比度弱，影响运动参数的精确估计。同时，当车牌部分在整幅图像中像素值占比过低时，低像素值会对其频谱图中模糊图像特性造成一定影响，即使准确估计出模糊参数，也很难使用复原算法清晰复原出模糊车牌的有效信息。因此，应进一步研究在精确估计模糊参数后如何能够清晰复原出像素值占比过低的模糊车牌图像。

四、结论

通过对运动模糊图像的频谱图进行对比度增强和干扰处理，再对处理后的频谱图使用Radon 变换估计模糊角度q，可以有效避免单帧监控视频模糊车牌图像频谱图中出现的十字亮条纹干扰，极大地提高了检测精度。在精确估计模糊参数后，采用运动模糊复原算法进行图像复原，结果表明模糊参数估计较为精确，可以较快的对单帧监控视频模糊车牌图像进行精确复原，从而获取车牌信息并及时为侦查人员提供重要线索。