“再建构”在初中数学试卷讲评课的有效运用

浙江省义乌市宾王中学 吕智英

在初中数学教学中，试卷讲评课有着不可替代的作用，这是一种基于学生基础开展的重要课型，也是基于“再建构”思想展开的教学分析工作。尤其对于初中阶段的学生来说，其思维能力正处于发展的重要时期，学生在学习完一个阶段的数学知识后就容易形成堆积，若不能够通过有效的形式促进学生对知识的巩固和理解，就会导致学生在实际解题的过程中出现各种各样的问题。

一、“再建构”在初中数学试卷讲评课中运用的意义

“再建构”是基于“学材再建构”的基础上延伸出来的新定义，这种定义主要是运用于日常教学中，通过碎片化知识的整合来让学生对知识形成整体的掌握，从而实现全面发展。实际上，将这种“再建构”的理念运用于数学试卷讲评课中的意义可以从两方面进行讨论：一是能帮助教师对数学试卷的内容进行分析，对学生试卷中存在的错题进行整合，从而高效帮助学生理解对应的数学知识。二是能够促进学生对知识的掌握和理解，在日常的数学试卷讲评课中，由于学生的思维还不够开阔，从而降低了教学的质量。通过这种“再建构”的理念进行教学，则能够帮助学生提高数学思维，从而加强课堂教学的效率。

二、“再建构”在初中数学试卷讲评课中运用的有效策略

1.关键信息重新构建，提高学生的认知能力

初中数学“再建构”思想主要是能够在钻研显性、隐形教材的基础上，让知识变得更加清晰，把握知识的关键点，找到适合学生的基本路径，从而通过有效的方式促进学生的成绩提升。这种“再建构”的思想是从“学材再建构”中提取出来的，是一种基于单元实施的教学理念，以教科书作为参照物，以学生的发展为主要目标，从而提高学生的实际成绩。对于初中数学试卷讲评课来说，这种教学仍然有着重要的作用。这是由于初中的试卷讲评课本就是以学生的发展为基本理念展开的，通过讲评、复习，让学生把握正确的数学观点。但这种试卷讲评往往只是对学生的引导，在实际解题时，无法有效地将材料中的信息转换为有用的数学知识点。因此，教师在实际的试卷讲评课中就可以通过再建构的思想，将试卷中的教学信息转换为可利用的数学知识点，从而提高学生的解题能力。

例如：已知一个三角形的三条边长分别为n+2，n+6，3n。

（1）n+2_n+6（填“＞”“＝”或“＜”）；

（2）若这个三角形是等腰三角形，求它的三边长；

（3）若这个三角形的三条边都不相等，且n为正整数，直接写出n的最大值。

教师首先要引导学生能够分析题意，这道题主要是求三角形的边长，要结合不等式的知识解决。在解第（2）（3）小题时，学生很容易忽略三角形的存在性这个隐含条件。因此，教师在进行教学时，就可以将这道题目的信息通过再建构变为学习过的三角形三边定理，从而引出构成三角形需要满足“任意两边之和大于第三边”这个条件。通过这样的方式将知识进行再构建，不但能够让学生形成自我探究的解题思路，还能够加强解题能力，从而有效化解在解决问题时的困惑，提高思维转换能力。

2.常见错题重点建构，加强学生的探究能力

在日常利用“再建构”的思想进行教学时，首先需要高度重视其应用的有效性，其次要能够根据题目中的主题内容去分析不同地区的题目和题型，并让学生能够学会整理错题。记录错题集，能够有效帮助学生在后续学习中进行知识的回顾，重点理解自己经常犯错误的知识点，从而提高数学思维，减少错误的发生。

图1

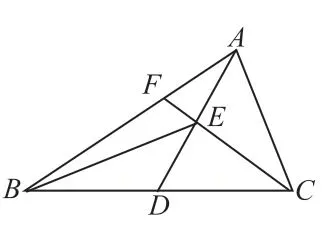
图2

图3

3.核心知识再次建构，促进学生的创新能力

“再建构”思想运用于试卷讲评课中，其一是为了能够让教师更好地把握教材、解读试卷中的基本信息，从而创新教学理念和教学方式，促进学生综合能力的发展，其二是为了能够打破单个知识点之间的界限，让碎片化知识能够进行有效的整合，从而帮助学生理清知识点之间的关系，透过现象看本质。事实上，基于这种“再建构”的思想的目的就是能够根据数学知识的内在联系，与学生学习的知识和试卷中的内容进行有效整合。因此，教师在实际的试卷讲评课中，就可以根据试卷中的知识将其分为不同的单元和模块，在讲解时便于实施，从而使学生能够从整体上对数学内容进行理解和掌握。

例如：下列命题中正确的是（ ）

A.对角线相等的四边形是矩形

B.对角线互相垂直且相等的四边形是正方形

C.对角线互相垂直的四边形是菱形

D.两组对角分别相等的四边形是平行四边形

学生出错的原因主要是知识点混淆不清，没有形成体系，教师就可以根据浙教版八年级下册“平行四边形”以及“特殊平行四边形”这两章内容组成一个完整的知识框架，如图4所示，帮学生理清各类四边形之间的联系与区别。通过这样的方式将试卷中的核心知识点进行再次建构，能够有效促进学生的学习能力和理解能力，从而提高学生的数学水平。

图4

总而言之，将“再建构”的思想融入初中数学试卷的讲评课中，不但可以给学生带来不一样的学习效益，还能够促进其数学思维的发展。当然，这种再建构的方式也是需要经过不断的拓展、探究、开发才能够真正形成适合学生的教学模式。因此，教师需要能够从实际出发，针对学生的实际情况研发出更多适合学生的理念，促进学生的发展。