基于GI/M/1 型Markov 过程的Geo/Geo/1多重工作休假排队系统分析
2021-06-19张宏波彭培让
张宏波, 彭培让
(河南财政金融学院统计与数学学院,郑州 450046)
1 引言
离散时间休假排队模型由于在计算机系统、控制系统、通讯系统等领域有重要的潜在应用价值,因而得到了大量的研究.详细的介绍可以参见文献[1—5].
Servi 和Finn[6]最先对M/M/1 排队引进了工作休假策略.在这种情形下,与普通休假不同,服务台不是完全停止工作,而是为在休假期间到达系统的顾客以较低的服务率提供服务.随后,各种含有工作休假策略的排队模型得到了大量的研究.特别是针对离散时间排队情形,例如,Li 等[7]研究了具有多重工作休假以及休假中断的GI/Geo/1 排队;Tian 等[8]研究了Geo/Geo/1 多重工作休假排队;关于多重工作休假的Geo/G/1 排队的详尽分析可参见文献[4].另外,Li 等[5]还研究了批到达的Geo/G/1 多重工作休假排队系统.
在Tian 等[8]对Geo/Geo/1 多重工作休假排队模型的研究中,作者把系统中的顾客数作为水平,把服务台的状态作为位相,对该排队系统建立了无限水平有限位相的QBD 过程模型.因为这时服务台要么位于正规忙期,要么位于工作休假状态,所以所得QBD 过程的位相只取2 个不同值.从而通过对模型求解,可得到平稳状态时服务台位于忙期或位于工作休假的概率.然而,对多重工作休假排队系统,因为当一次休假结束时,只要系统仍然没有顾客,服务台将进入另一个独立休假.因此,休假可以连续进行,这样,我们应考虑已知服务台位于工作休假状态时,它具体位于第几次工作休假的概率,这一问题用文献[8]中的模型无法直接回答.鉴于此,在本文中,我们对该排队系统应用无限位相GI/M/1 型Markov 过程重新建模,通过对该过程的求解,不但可得该模型的经典结果,如平稳队长分布等,还对上述问题作了回答.所得新结果使得对服务台状态的刻画更为具体.
在本文的其余部分,首先,在第2 节给出所研究排队系统的一个新数学模型;然后,在第3 节对模型求解,并对本文讨论的排队系统进行分析;第4 节给出若干数值例子;最后,第5 节是小结部分.
2 模型描述
对经典的Geo/Geo/1 多重工作休假排队系统,假设顾客的到达发生在时隙(n,n+), n≥0,顾客的离去发生在时隙(n-,n), n ≥1,按照Hunter[9]的约定,本文考虑的是早到系统.设到达间隔独立同分布,共同的分布是参数为p的几何分布而服务时间服从参数为q的几何分布.假设休假时间服从参数为θ的几何分布,且在休假期,系统为到达的顾客提供服务的速率为η,其中η <q.另外,在本文中,对任意实数x ∈(0,1),定义¯x=1-x.
令Ln表示时刻n时系统中的顾客数,则按照早到规则,在时隙(n-,n)离去的顾客不再计入Ln.令Jn表示时刻n时服务台的状态,且规定Jn= 0 表示服务台位于正规忙期,而对k ≥1,Jn=k表示服务台位于工作休假状态且恰好位于第k次休假.考虑二维Markov 过程{Jn,Ln,n ≥0},其状态空间为

其中对l ≥1,状态(0,l)表示服务台位于正规忙期且这时系统中有l个顾客;对k ≥1 及l ≥0,状态(k,l)表示服务台位于第k次工作休假且系统中有l个顾客.
当把状态按字典规则排序时[10],上述Markov 过程的转移概率矩阵具有如下所示的分块矩阵形式

其中A0=diag{¯pq,0,0,···},A=diag{¯pθ,0,0,···},

因此,所得过程是一个无限位相的GI/M/1 型Markov 过程[11].

都是无穷维向量,这时由文献[11]知平稳分布满足如下所示的算子几何解

其中R 是一个无穷维矩阵,称为率算子且对本文所讨论的情形,它是下述矩阵方程的最小非负解

另外,初始向量π0和π1由线性方程组
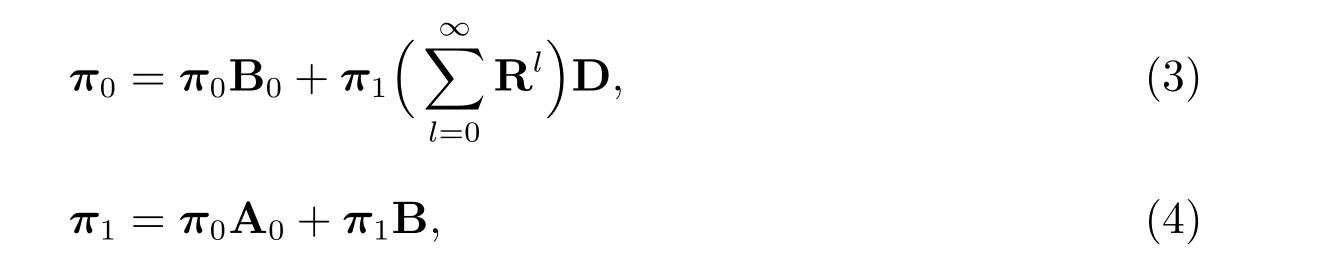
以及规一化条件共同确定.
3 平稳分析
本小节对所建立的模型求解,并对排队系统的平稳状态进行分析.为了求解模型,首先给出率算子R 以及初始分量π0和π1,有下述两个引理.
引理1 率算子R 的具体形式如下所示
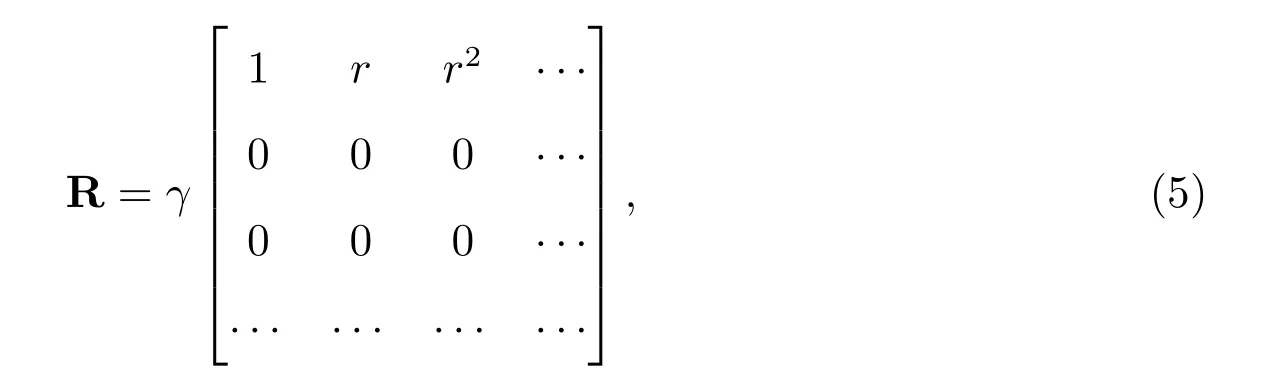
其中

都是位于(0,1)中的常数.
证明 由率算子的概率解释[10]可知对本文讨论的模型,R 除了第一行外其余各行元素皆为0.现在令(r0,r1,···)表示其非零行,则通过简单的代数运算可知方程(2)的分量形式为
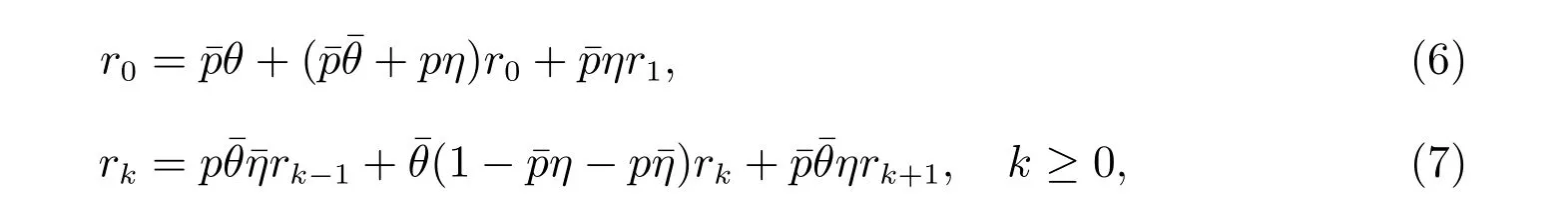
其中方程(7)是一个二阶线性齐次差分方程,且特征方程为

从而易得其两个特征根为
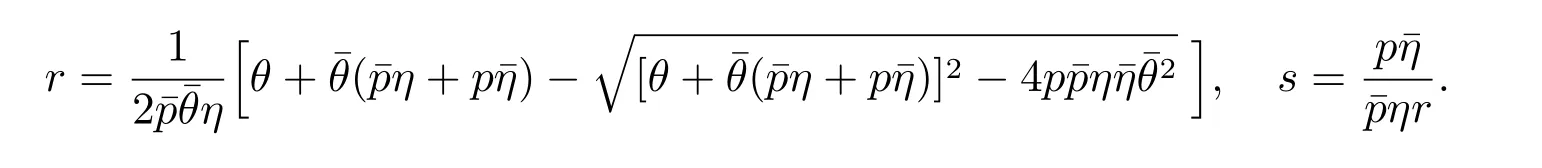
因此

这里γ和δ都是待定常数.另外,由常规的代数运算容易验证r ∈(0,1), s >1,所以为了得到方程(2)的最小非负解,常数δ必须为0,因而由(6)可知

由此即得引理的结论.
引理2 在平稳分布中,初始向量π0和π1的分量由以下两式给出
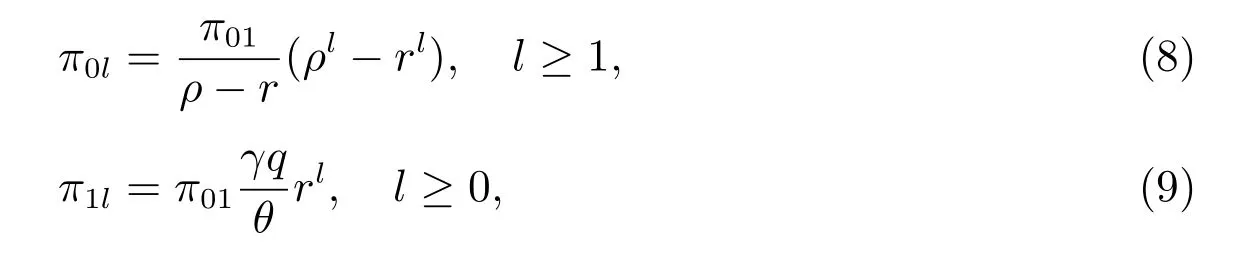
其中π01待定.
证明 因为π0和π1满足线性方程组(3)和(4),由各子矩阵的具体形式,易知方程(4)的分量形式为
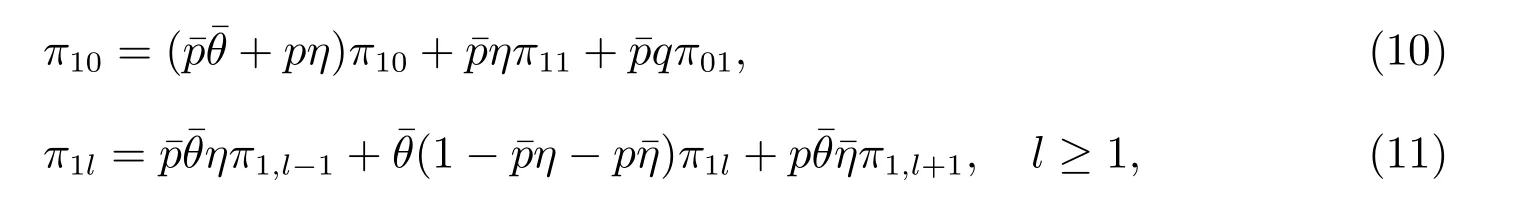
其中方程(11)是一个二阶齐次线性差分方程,由类似于引理1 中的方法可得其收敛解为
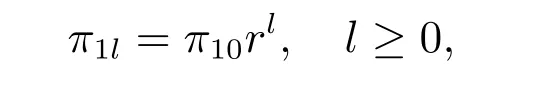
因而π11=rπ10,代入(10)式后化简,再由γ的定义可得

由此即得(9)式.
其次,由(5)出发可以验证

所以有
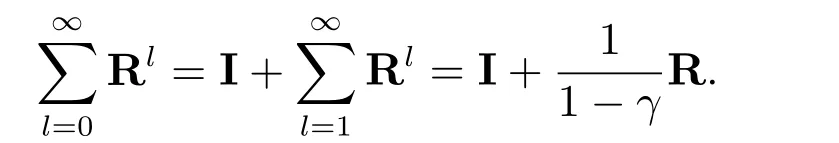

把上式代入方程(3)后,并利用(9)进行化简,可得其分量形式为

最后,由π1l的表达式和(15)式,可得

再由(12)式以及γ的定义,把上式右边化简可得
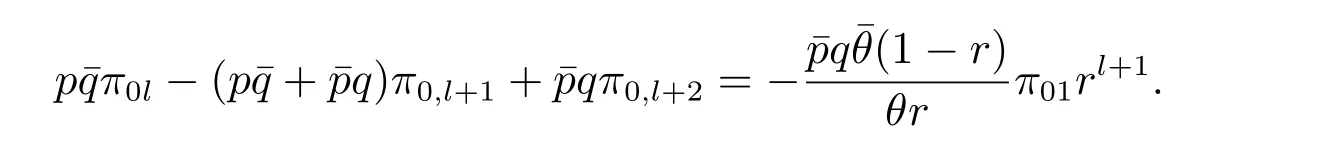
这是一个二阶非齐次线性差分方程,且当ρ <1 时,易求得其唯一收敛解为
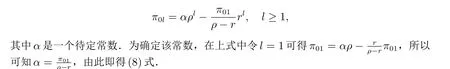
有了引理1 和引理2,现在给出本文的两个主要结论如下.
定理1 令bl表示平稳状态时服务台处于正规忙期且系统中有l个顾客的概率,令wk表示平稳状态时服务台处于休假状态且恰好处于第k次休假的概率,则有
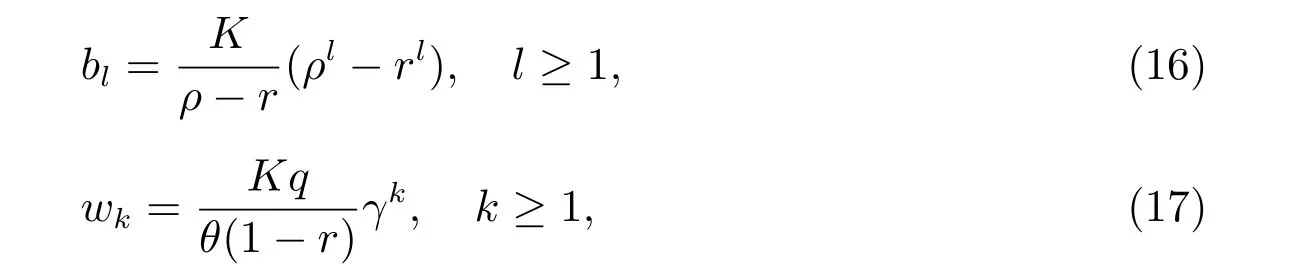
其中

是一个常数.
证明 首先给出Markov 过程的联合平稳分布.由算子几何解(1)式以及(9)式和(13)式,可得
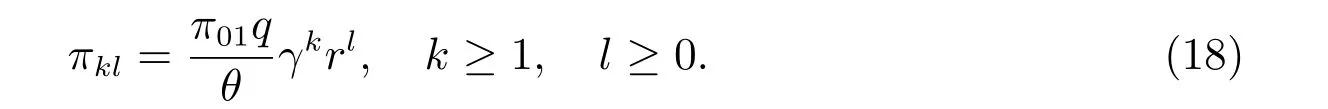
因此,再由(8)式以及归一化条件可得

推论2 令Nw表示平稳状态时服务台在一次工作休假期连续进行休假的次数,则有

可得推论的结论.
定理2 令L表示平稳状态时系统中的顾客数,则有

其中K的定义见定理1.
证明 因为
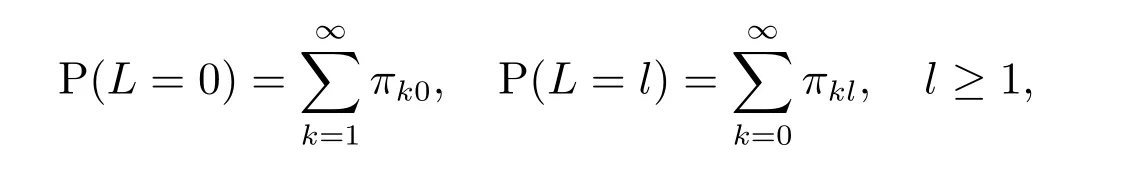
再由(8),(18)两式出发,经过计算易得.
在方程(19)的基础上,可以进一步讨论该排队模型平稳队长和平稳逗留时间的随机分解结果,相应的结果可参见文献[8].
4 数值例子
在前面的分析中,我们得到了Geo/Geo/1 多重工作休假排队一些平稳指标的结果,特别是得到了平稳状态时服务台位于第k次休假的概率wk以及一个休假期内连续休假次数Nw的分布以及平均次数,这些是关于该排队模型的新结果.本小节用数值例子对上述新指标进行分析,考虑这些指标随着某些参数变化的规律.其它指标,如平稳队长、平稳逗留时间随某些参数的变化情形可以参见文献[8].
第一个例子考虑平稳状态时服务台位于第k次休假的概率wk随k变化的情形.首先,令q= 0.6, θ= 0.3, η= 0.3,对p= 0.1,0.3,0.5 三种情形下wk的变化曲线,如图1(a)所示.由该图可以看出,当p固定时,wk随k的增加而减少;同样地,当k固定时,wk也随p的增加而减少.
其次,令p=0.3, q=0.7, θ=0.3,对η=0.1,0.3,0.5 三种情形下wk的变化曲线,如图1(b)所示.由该图可以看出,这时曲线的变化规律与前一情形类似.
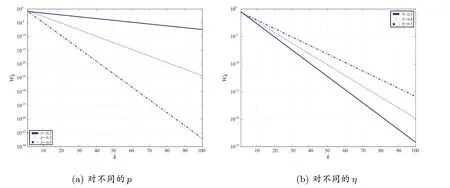
图1 位于第k 次休假的概率wk 随k 的变化曲线
第二个例子考虑一个休假期间平均休假次数ENw随某些参数的变化规律.首先是ENw随p的变化情形,令q= 0.7, θ= 0.3,0.4,0.5,令p ∈[0.3,0.6].相应的曲线如图2(a)所示.由该图可以看出,当θ固定时,ENw随p的增加而减小;但对固定的p,ENw随θ的增加而增加.
其次,考虑ENw随η的变化情形,令p= 0.6, q= 0.8, θ= 0.3,0.4,0.5,令η ∈[0.1,0.5].相应的曲线如图2(b)所示.由该图可以看出,当θ固定时,ENw随η的增加而增加;同时对固定的η,ENw随θ的增加而增加.
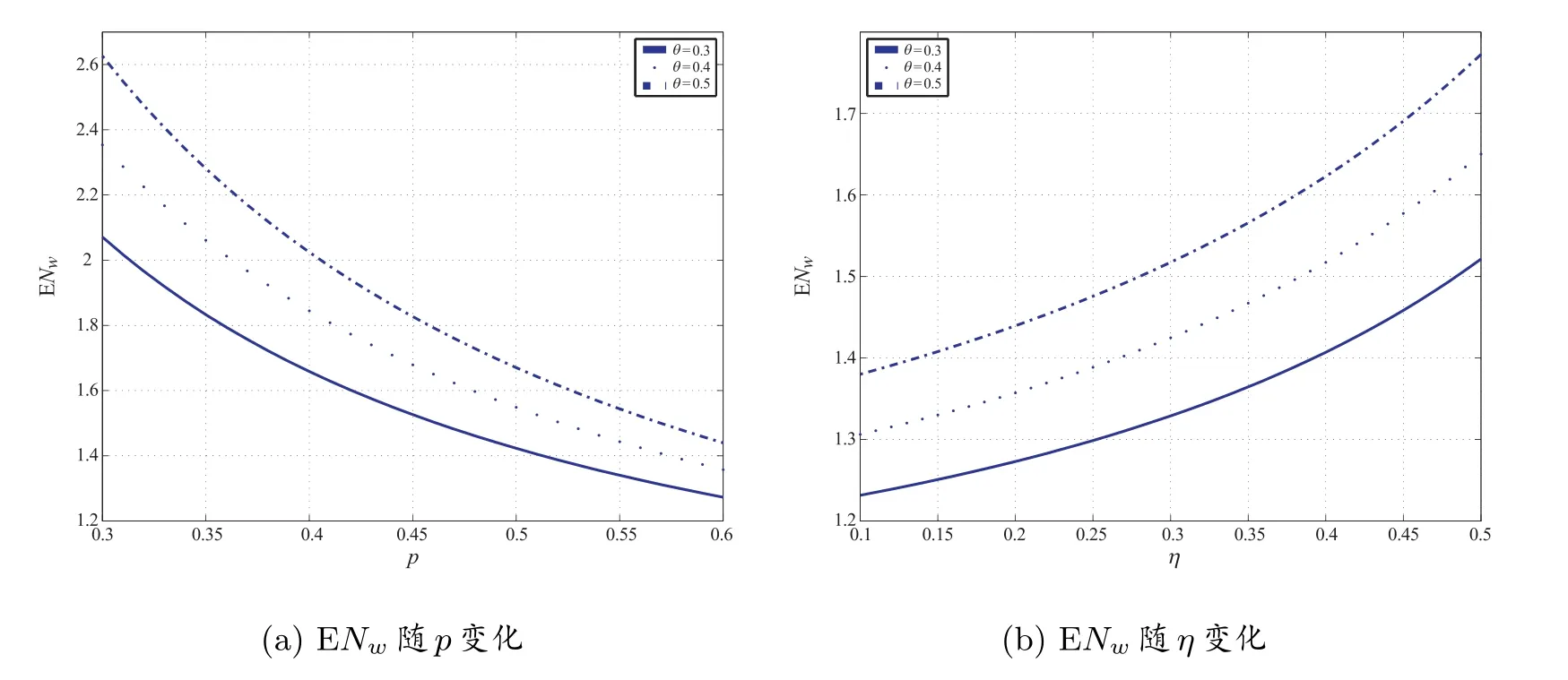
图2 一个休假期平均休假次数ENw 随参数的变化曲线
5 小结
本文用一种新的方法讨论了经典的Geo/Geo/1 多重工作休假排队系统,给出了一些新的结论,它们对排队模型平稳状态时服务台的状态进行了更为细致的刻画,因而,具有重要的意义.
另外,应用本文方法能否对其它多重工作休假排队模型如M/G/1 工作休假排队或GI/M/1 工作休假排队进行研究,是有意义的值进一步考虑的问题.
