分布式变量选择—MCP 正则化
2021-06-19王格华王璞玉
王格华, 王璞玉, 张 海
(西北大学数学学院,西安 710069)
1 引言
考虑线性回归Y=Xβ+ε,其中X ∈RN×p是输入变量,Y ∈RN是输出变量,β ∈Rp是该模型的系数向量,ε是随机误差.当模型稀疏时,即真实β的大部分分量等于零,我们考虑用稀疏正则化方法来解决此问题.通常,正则化方法具有如下形式

其中Y= [Y1,Y2,··· ,YN]T ∈RN, X= [X1,X2,··· ,XN]T ∈RN×p,λ >0 是调控参数,用来控制模型的复杂度.当k= 0 时,上述正则化框架对应于AIC 或BIC[1,2],此时它被称为L0正则化.虽然L0正则化可以得到最稀疏的解,但求解它对应于一个NP 难问题.因此,众多学者提出了不同的正则化方法来逼近L0正则化,其中包括Lasso 方法(当k= 1 时)[3-7].为了得到更稀疏的解,许多学者提出了非凸正则化方法,包括Adaptive Lasso[8]、Smoothly Clipped Absolute Deviation(SCAD)[9]、Minimax Concave Penalty(MCP)[10]、L1/2正则化[11]等.特别地,MCP 方法的提出作为一种经典的非凸正则化方法,具有许多理想的性质,并且已经被广泛研究[12-15].它具有以下形式

其中λ ≥0, γ >1.
上述正则化方法的提出和发展为我们处理和分析海量高维数据提供了有效工具,但其仅适合于单机数据处理,即数据存于同一个机器中.随着信息的发展,大量的生物科学和医学数据由于数据量巨大而采用分布式存储方式.因此,设计和研究适合于处理分布式数据的机器学习算法是当前数据分析关注点之一.针对分布式数据存储的新特点,Mateos 等[16]提出了将分布式计算与正则化方法相结合的分布式Lasso 方法,Wang 等[17]提出了分布式L1/2正则化方法.鉴于非凸正则化对变量选择和特征提取的优越性,我们关注基于分布式计算的非凸MCP 正则化方法.
本文研究分布式MCP 方法.首先,依数据所属计算机的不同,提出分布式MCP 模型;其次,基于ADMM 算法,提出分布式MCP 算法并证明它的收敛性.最后,通过模拟实验和真实数据实验,证明所提方法在处理海量分布式存储的数据的有效性.
2 分布式MCP 模型

模型(3)将所有数据拆为J个部分,其与原模型(1)等价.
为了使每台计算机能够不依赖其他计算机独立的进行计算,我们考虑用局部变量{βj}替换全局变量β,其中βj为每台计算机的局部估计.那么模型(3)可改写为下述分布式MCP 模型

3 分布式MCP 算法
本节基于ADMM 算法求解分布式MCP,并给出算法的收敛性分析.
3.1 ADMM 算法
ADMM 算法于20 世纪70 年代早期被提出[18,19],随后被众多学者推广[20-24].近年来,ADMM 算法在计算机视觉,信号处理等诸多领域被广泛应用.本节借助ADMM 算法求解分布式模型(4).首先,考虑添加辅助局部变量,则模型(4)可以改写为

模型(5)要求网络中所有局部变量彼此相等,注意到我们假设图G= (J,E)是连通的,那么(3)和(5)是等价的.
为了方便表述,我们将模型(5)写成向量的形式

其中
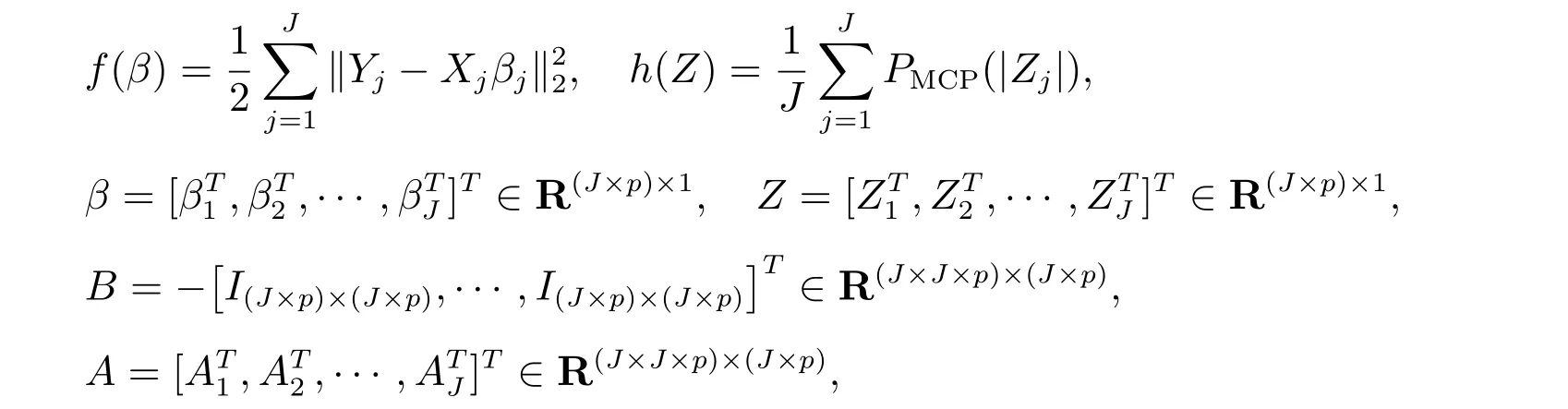
其中A*=[Ip×p,··· ,Ip×p]T ∈R(J×p)×(p),0∈R(J×p)×p是零矩阵,A1=[A*,0,··· ,0],A2=[0,A*,··· ,0],··· ,AJ=[0,··· ,0,A*].
模型(6)的二次增广拉格朗日函数为
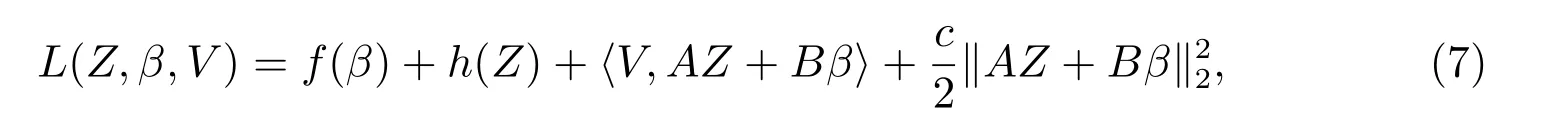
其中V ∈R(J×J×p)×1为拉格朗日乘子,c >0 为预选参数.
ADMM 算法分为以下三个步骤:
步骤1 更新Z

步骤2 更新β
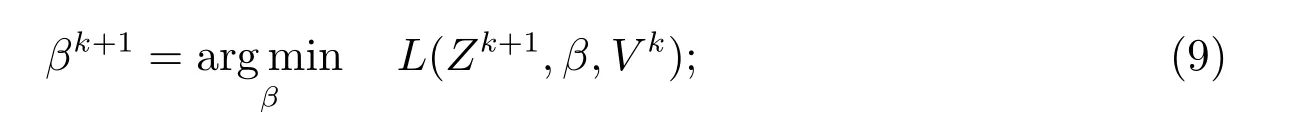
步骤3 更新拉格朗日乘子
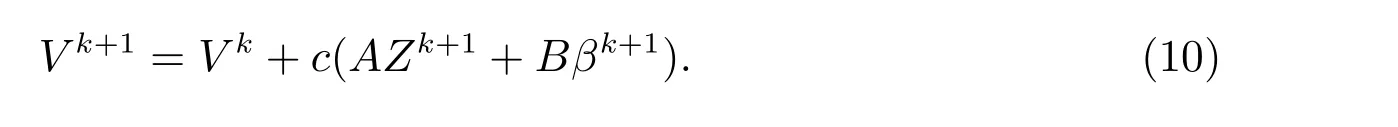
在分析ADMM 算法的收敛性之前,我们给出一些记号.令∂f表示函数f的次梯度,M表示矩阵ATA的最小正特征值,M′表示矩阵BTB的最小正特征值.如果一个函数可微且梯度是李普希兹连续的,我们称这个函数李普希兹可微.显然,模型(6)中的f(β)是李普希兹可微的,且李普希兹常数为Lf.对于任何Z1, Z2,都有下式成立,存在ω ≥1,
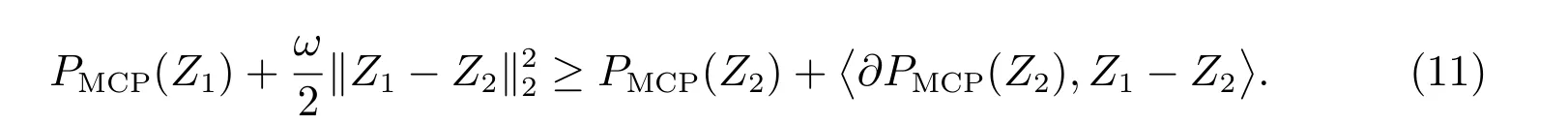
对于[Z2]的每个维度[Z2]i,若[Z2]i= 0,则[Z2]i的广义次梯度在[-1,1]之间,如果ω足够大,那么对于任何Z1,我们都有

若[Z2]i/=0,则[Z2]的二阶梯度为0 或-1/γ,那么

故(11)成立.
下面,我们给出几个引理和主要的收敛定理.
引理1 对于所有的k,下面的结论成立:
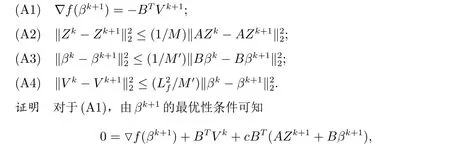
且
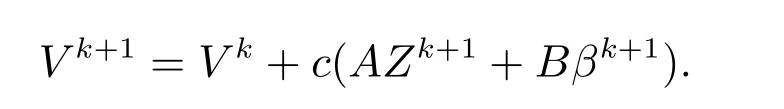
由于M和M′分别为ATA和BTB的最小正特征值,则(A2)和(A3)显然成立.
(A4)可由下式得到
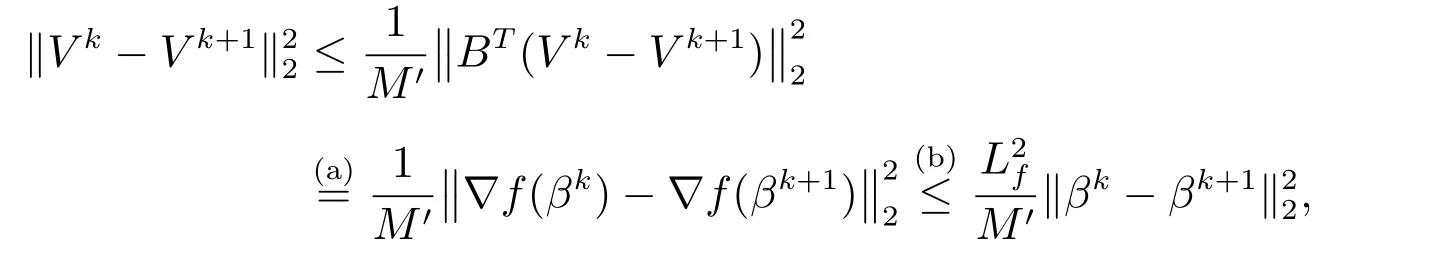
其中,利用引理1(A1),(a)成立;注意到f是李普希兹可微的,(b)成立.
引理2 若c >max{Lf/2M′,LfM′,ω/JM},则当k →∞时,L(Zk+1,βk+1,V k+1)收敛.
证明 首先,我们证明在选取合理的预选参数c的情况下,L(Z,β,V)在每次ADMM迭代期间递减.
我们将增广拉格朗日函数之差拆分为


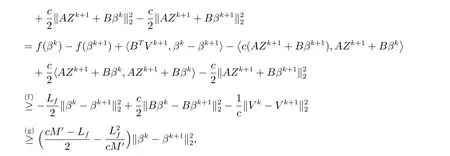
考虑第一项其中,利用引理1(A1)和f为李普希兹可微的,(f)成立;利用引理1(A3)和引理1(A4),(g)成立.由上述两项得到的不等式,ADMM 算法中的迭代满足下式

如果c >max{Lf/2M′,ω/JM},则在ADMM 迭代期间L(Z,β,V)单调递减.
下面,我们证明增广拉格朗日函数对任意k都有界.
对于任意一个Zk+1,存在β′,使得AZk+1+Bβ′=0,那么
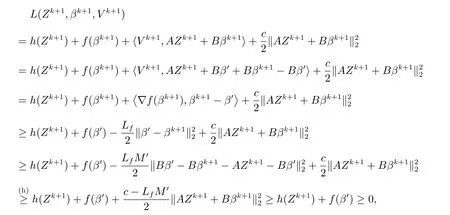
其中,在(h)中我们假设c >LfM′,则L(Zk+1,βk+1,V k+1)有下界,进而当k →∞时,L(Zk+1,βk+1,V k+1)收敛.
引理3 存在dk+1∈∂L(Zk+1,βk+1,V k+1),使得当k →∞时,→0.
证明 首先,有
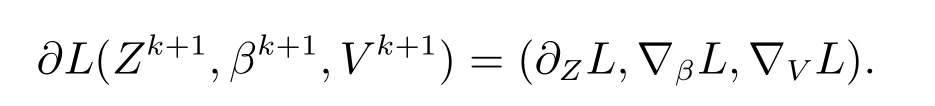
因为∇V L=AZk+1+Bβk+1=(1/c)(V k+1-V k),且由引理1(A4),不等式
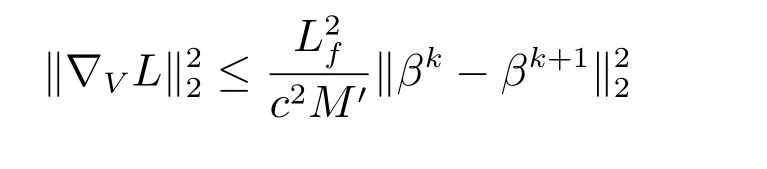
成立.同时,我们有
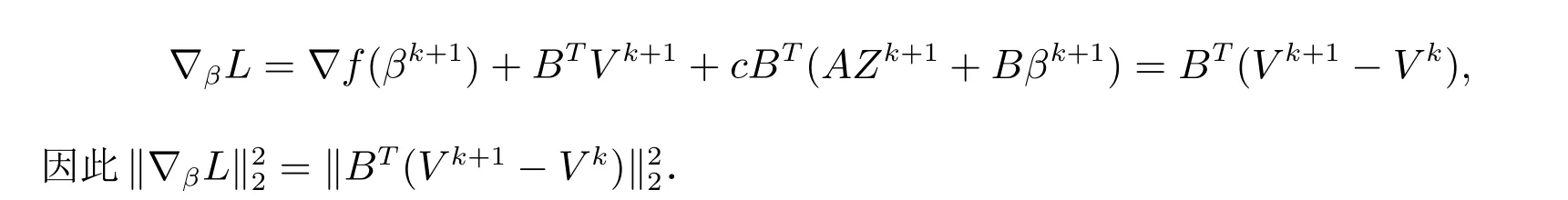
又因为
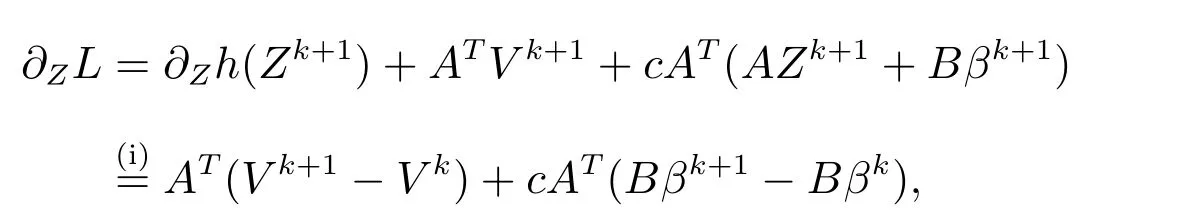
其中,利用Zk+1的最优性条件,(i)成立,则有

基于上述三个引理,我们给出ADMM 算法收敛性定理.
定理2 若c >max{2Lf/M′,LfM′,ω/M},则由ADMM 算法(8)—(10)产生的序列收敛到L(Z,β,V)的驻点.
3.2 参数估计
为了求解ADMM 算法的三个步骤,我们改写增广拉格朗日函数
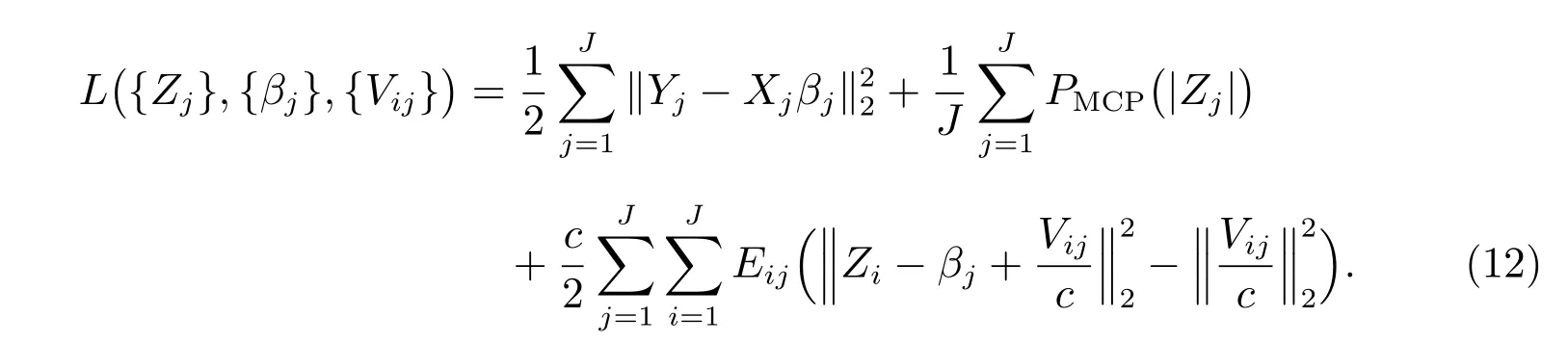
首先,考虑{Zj}的更新,令

根据数据所属计算机的不同,我们将(8)分解为J个子问题
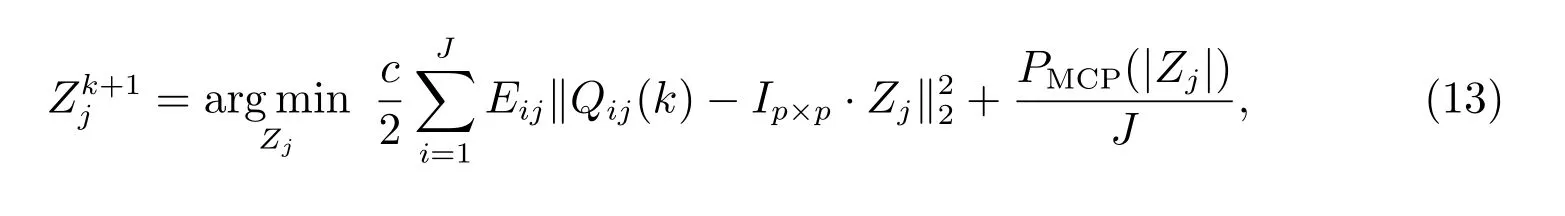

下面,我们给出坐标下降法的收敛性分析.
引理4 对于m= 1,2,··· ,p,令Oj,m为目标函数O关于变量Zj的坐标m的函数,Zj其它坐标是固定的.如果预选参数c >1/(γ*J),则对于所有坐标m,Oj,m是关于[Zj]m的一个凸函数.

证明 假设预选参数c >1/(γ*J),则对于每个计算机j,和所有维度m, O是关于[Zj]m的严格凸函数.O的严格凸性和连续性满足文献[26]中定理4.1 和定理5.1 的条件,进而坐标下降算法收敛到坐标最小值.由于O的所有方向导数都存在,因此每个坐标最小值也是局部最小值.
从引理4 中我们可以看出,当预选参数c >1/(γ*J)时,对于任何一个j ∈J,尽管目标函数O包含非凸的MCP 罚项,它仍是一个关于[Zj]m的凸函数.在XTX和c满足某些条件时,目标函数L(Z,β,V)为凸函数.在这种特殊情况下,(15)收敛于目标函数(13)的全局最小值.
下面,我们考虑β的更新,它也可以分解为J个子问题

同样,通过使用坐标下降法,给出局部βj的第m个坐标的显式解
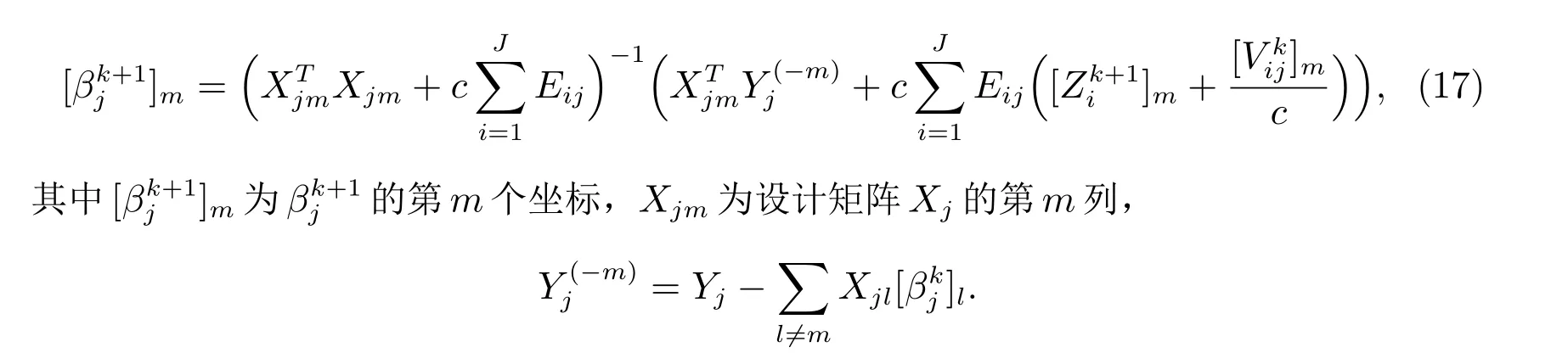
注1 如果计算机i与计算机j不连接,则Eij=0.这意味着我们在更新Zj和βj时,只需要计算机j的邻居的信息.
结合(15),(17)和(9),我们提出如下分布式MCP 算法.
算法1 分布式MCP 算法

对 ∀j ∈J, 令β =(1,··· ,1)T, Z =(1,··· ,1)T, Vij =(1,··· ,1)T,局部运行for k =1,2,···第j 台计算机在Nj 与邻居传递信息对于m=1,2,··· ,p利用(15)更新[Zk+1 j ].end for l=1,2,··· ,p利用(17)更新[βk+1 j ].end通过(10)更新拉格朗日乘子V.end

3.3 分布式k 折交叉验证
下面,我们给出分布式k折交叉验证算法,以此来选择惩罚参数λ.


重复上述步骤,我们可以计算每个λi的均方误差MSE,使得

最终,我们选择预测误差最小的λdcv=arg minλi{e(λi)}作为调控参数.
4 实验
本小节,我们通过4 个实验来说明算法的有效性.其中,实验1 通过模拟数据说明算法与非分布式算法有相同的变量选择结果.实验2、实验3 通过设计大数据量数据说明算法适合于大数据的分析处理.实验4 通过实际数据说明算法的实用性.
4.1 实验1(模拟实验)
在这个实验里,对于我们考虑的线性模型
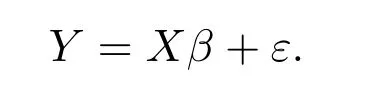
我们设置变量数量p=8,具体地β=(3,1.5,0,0,0.5,0,0,0), X=(X1,X2,··· ,X8).Xj~N(0,Σ),Σ = (σij), σij= 0.5|i-j|,1≤i,j ≤n.当应用分布式MCP 方法时,我们将所有数据划分为J=5 组,并选择邻接矩阵

我们模拟了100 个数据集,每个数据集包含100 个观测值.我们分别应用Lasso 和分布式MCP 处理这100 个数据集.其中,我们用LARS 求解L1正则化.当应用分布式MCP 方法时,用分布式5 折交叉验证来选取调节参数λ,预选参数c= 0.1.我们记录100 组数据集上的正确识别零系数的平均数(C.A.N),以及错误识别的零系数的平均数(IC.A.N),结果如表1 所示.
从表1 中可以看出,非分布式MCP 与分布式MCP 有相同的变量选择结果,其C.A.N是4.45,多于Lasso 的C.A.N 的2.26,这表明,分布式MCP 的变量选择结果比Lasso 稀疏.C.A.N 为在100 个数据集上,结果模型和真实模型中值均为0 的系数个数的平均值;IC.A.N 为在100 个数据集上,结果模型中值为零但在真实模型中值为非零的系数个数的平均值.

表1 Lasso 和分布式MCP 在实验1 中的结果
4.2 实验2
在这个实验中,我们模拟数据集n= 100000, p= 100,其中(β1,β2,··· ,β20) =(50,49,··· ,30),(β21,β22,··· ,βp)=(0,0,··· ,0),预选参数c=0.1, X=(X1,X2,··· ,Xp).Xj~N(0,Σ),Σ = (σij), σij= 0.5|i-j|,1≤i,j ≤n.当应用分布式MCP 方法时,我们将所有数据划分为J= 5 组,并选择邻接矩阵E.分布式MCP 方法变量选择的结果呈现为图1.

图1 当n=100000, p=100 时,分布式MCP 方法变量选择的结果
上述实验结果表明,对于非分布式算法,单机很难处理的数据量较大的问题,分布式MCP 正则化可以对其进行变量选择.进一步,所提出的方法适合当今分布式处理数据的需求.
4.3 实验3
在这个实验中,我们比较了Lasso 和分布式MCP 方法的计算效率.我们分别令n=105,106,107,3×107,5×107和p=10,100,并生成7 个数据集.在模拟实验中,我们使用LARS 来求解L1正则化.然后我们运行了Lasso 和分布式MCP 方法,并比较了两种算法的计算时间.结果如表2 所示.当n=3×107,5×107, p=10 时,Lasso 失效,而分布式MCP 依然可以有效运行.
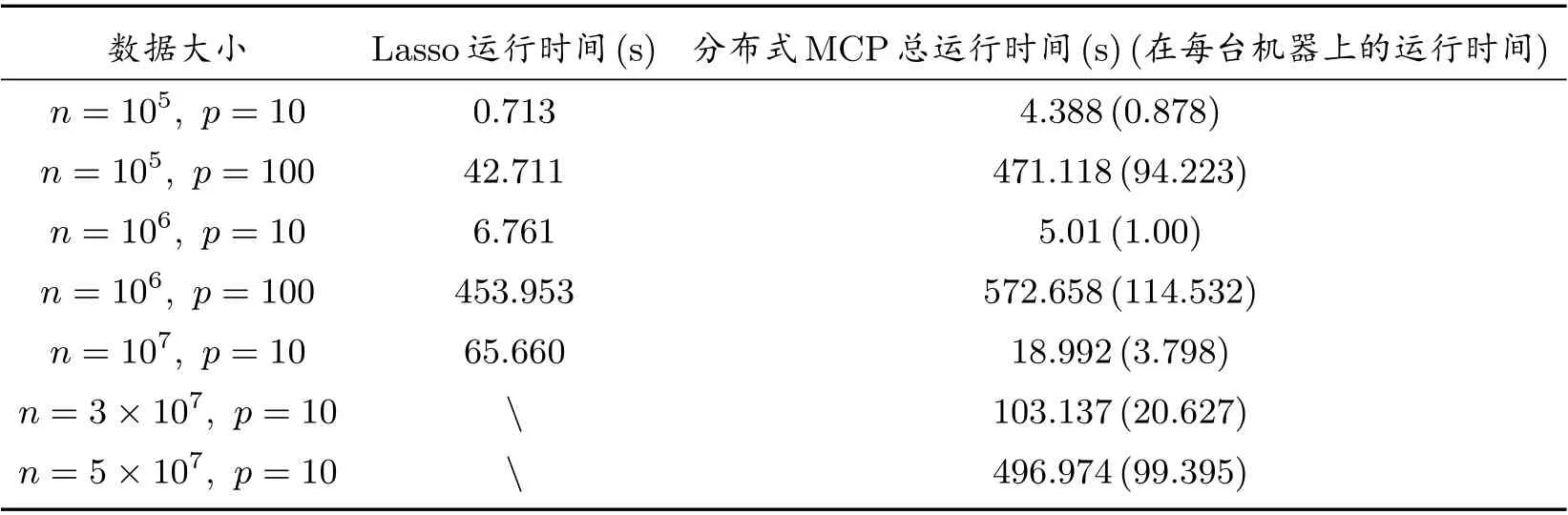
表2 Lasso 和分布式MCP 在7 个数据集上的运行时间结果
实验表明,当n= 105,106,107, p= 10,100 时,Lasso 和分布式MCP 均可以有效地选择变量;当n >3×107时,Lasso 失效,但是分布式MCP 仍然可以有效运行.
4.4 实验4(前列腺数据)
在这个实验中,前列腺病人数据来源于UCI 标准数据库中前列腺病人的相关数据,数据集大小为97.我们研究病人的抗原水平与肿瘤体积记录(lcavol),前列腺重量记录(lweight),年龄(age),良性前列腺增生量(lbph),精囊浸润(svi),包膜穿透记录(lcp),Gleason 积分(gleason)以及Gleason4 或5 所占的百分比(pgg45)等8 个指标之间的关系.将8 个指标看做输入变量,将病人的抗原水平看做输出变量,在对数据进行预处理后,我们用Lasso 和分布式MCP 算法对数据集进行变量选择,并观察实验结果.
在运行分布式MCP 方法时,本文将所有的样本数据分配给5 台计算机,调控参数λ由分布式5 折交叉验证来选择,邻接矩阵为E,预选参数c= 0.1.Lasso 选择结果如图2 所示,共有5 个变量选进模型,均方误差为0.7531.分布式MCP 选择结果如图3 所示,共有3 个变量选进模型,均方误差0.5029.分布式MCP 选择结果比Lasso 少选择了两个变量,这说明分布式MCP 方法可以更有效地解决该类问题,相比L1可以得到更稀疏的解.
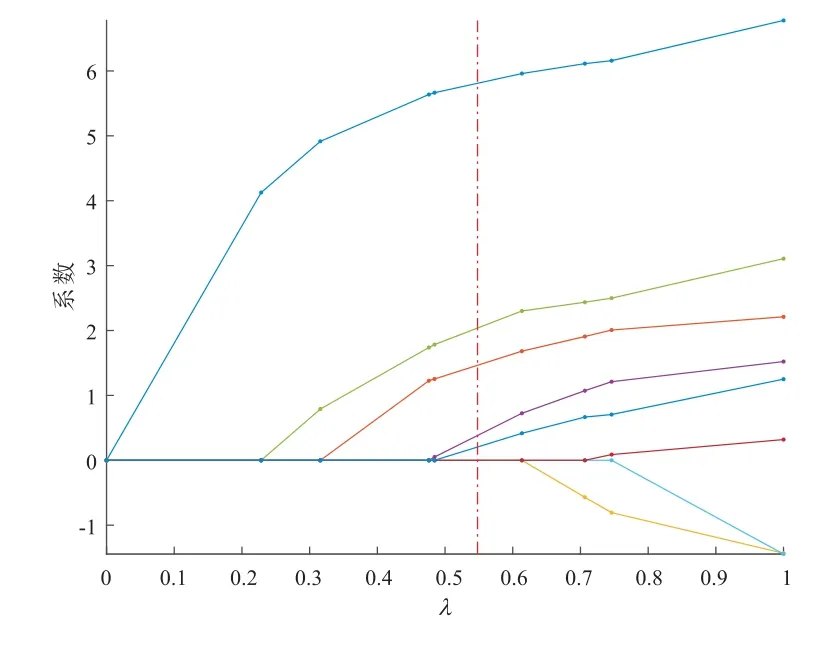
图2 Lasso 选择结果
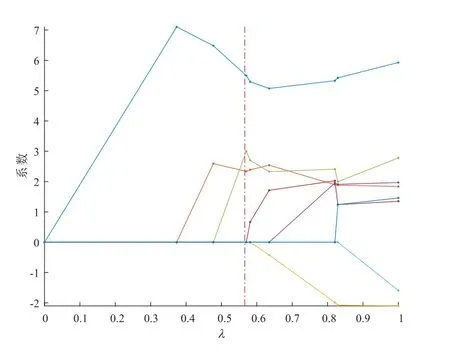
图3 分布式MCP 选择结果
5 结论
本文研究分布式MCP 方法,依据数据所属计算机的不同,将MCP 模型转化为等价的分布式MCP 模型.基于ADMM 算法,我们提出了分布式MCP 算法并证明了它的收敛性.分布式的变量选择结果与非分布式方法变量选择结果相同.实验表明,分布式MCP 方法能够有效的处理分布式存储的数据.进一步,本文提出的方法可以推广到其他分布式非凸方法.所有这些问题都在我们目前的研究之下.
