基于Karatsuba和Vedic算法的快速单精度浮点乘法器
2021-06-19易清明符清杆骆爱文陈嘉文
易清明,符清杆,石 敏,骆爱文,陈嘉文
(1.暨南大学信息科学技术学院 广州510632;2.泰斗微电子科技有限公司 广州510663)
单精度浮点数乘法运算的耗时主要集中在24 bit的尾数相乘部分。为了提高单精度浮点数乘法运算的速度,研究者提出了各种单精度浮点乘法器的改进方法[1-8]。文献[1]提出了基于Karatsuba算法[9-10]的改进设计,通过数学运算的公式变换,用加法器代替乘法器,相比于24 bit尾数直接相乘的单精度浮点乘法器的设计,该设计减少了3个乘法器,只使用了6个乘法器。但是乘法器的使用限制了单精度浮点乘法器运算速度的进一步提高。文献[2]提出了一种基于Vedic算法[3-4]的单精度浮点乘法器设计方法,该设计沿用了24 bit尾数直接相乘的设计思路,通过使用Vedic算法设计3 bit的乘法器,迭代复用,实现24 bit的尾数相乘运算,从而避免乘法器的使用,提高单精度浮点乘法器的运算速度。但是简单使用Vedic算法设计单精度浮点乘法器,导致Vedic算法设计的3 bit乘法器迭代次数过多,硬件资源增多。文献[3]沿用了Vedic算法的思想,利用流水线设计方法对单精度浮点乘法器结构进行优化,同时减少单精度浮点乘法器的组合逻辑延时,提高单精度浮点乘法器的运算速度,但是同样存在Vedic算法设计的3 bit乘法器迭代次数过多,硬件资源增多的问题;文献[5]在Vedic算法的基础上,通过全加器的复用来简化单精度浮点乘法器的设计结构,提高单精度浮点乘法器的运行速度,但是依然无法满足目前的运算需求。
以上文献提出的改进方法对单精度浮点乘法器的运算速度均有一定的提高,但是人工智能的兴起对浮点数乘法运算的速度提出了更高的要求,数以百万计的浮点数乘法运算造成深度学习的训练时间过长,限制了人工智能的研究与实用性。为了进一步提高单精度浮点乘法器的运算速度,本文利用Vedic算法改进了Karatsuba算法,并把该算法应用于单精度浮点乘法器设计。
1 浮点数乘法原理
本文设计的单精度浮点乘法器基于IEEE754标准[11]。单精度浮点数的表示格式由4字节组成,分为3个部分。第1部分为符号位,占1 bit;第二部分为阶码部分,占8 bit;第三部分为尾数部分,占23 bit。一个实数H的浮点数表示形式为:

式中,C表示符号位;Z表示尾数部分,在浮点数运算时要补上隐藏的‘1’,转换成{1,Z};E表示阶码,在实数转换为浮点数格式时要减去相应的偏移量。
单精度浮点数乘法运算可以简单分为4个步骤。
1)两个乘数的符号位进行异或运算。根据异或的结果决定最后计算结果的正负性。若符号位异或的结果为1,则浮点数相乘的结果是负数,若异或的结果为0,则浮点数相乘的结果是正数。
2)两个乘数的阶码直接相加,其结果再减去偏移量Bias得到相乘后结果的阶码,Bias的值为127。
3)尾数部分补上隐藏的‘1’,执行尾数相乘操作,得到相乘的结果V。
4)步骤3)相乘结果V的最高位的值决定标准化结果尾数的取值。若最高位为1,则取V[46:24]位作为最后标准化结果的尾数;若最高位是0,则取V[45:23]位作为最后标准化结果的尾数。联合符号位的值、阶码的值和尾数的值到两个浮点数相乘的结果。
浮点数乘法运算的流程如图1所示。Ha、Hb表示32位的浮点数,Za、Zb为23 bit的尾数。Ha的符号位与Hb的符号位进行异或运算得到符号位部分运算后的结果;Ha的阶码加上Hb的阶码再减去相应的偏移量(Bias)得到阶码部分运算后的结果;尾数在高位补上隐藏的‘1’,分别得到24 bit的乘数{1,Za}、{1,Zb}。24 bit的乘数相乘得到48 bit的结果V,其最高位的值决定浮点数相乘结果尾数的取值。联合符号位部分运算后的结果、阶码部分运算后的结果及尾数部分标准化的结果得到浮点数相乘的结果。由于尾数部分的标准化需要依据V最高位的值,所以尾数相乘的耗时决定了浮点乘法器的运算速度。

图1 浮点数乘法运算的流程框图
2 Karatsuba算法
传统单精度浮点乘法器中的尾数相乘实现方法如下所示[1]:
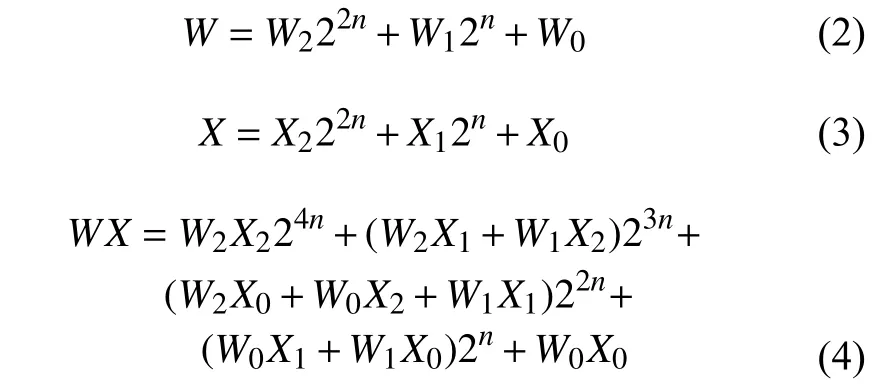
式中,n取值为8;W、X(W={1,Za},X={1,Zb})为24 bit的尾数;W2、W1、W0分别表示W的高8位、中8位、低8位;X2、X1、X0分别表示X的高8位、中8位、低8位。传统的单精度浮点乘法器设计把尾数W和X直接相乘,由式(4)可知,得到24 bit尾数相乘的结果需要9个8位×8位的乘法器和8个加法器。由于乘法运算比加法运算耗时长,且电路结构更加复杂,所以传统的单精度浮点乘法器效率比较低且运算速度慢。Karatsuba算法用加法器来替代乘法器,从而减少乘法器的使用,达到简化电路结构,提高运算速度的目的。基于Karatsuba算法的24 bit尾数相乘的实现方法具体如下所示[1]:

根据式(5)~(10)可以得到24 bit尾数相乘的结果,如下所示:
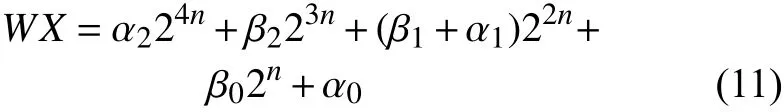
由式(11)可得,相比于传统方法实现的24 bit尾数相乘,基于Karatsuba算法实现的24 bit尾数相乘使用的乘法器数量更少,由之前的9个乘法器减少到6个乘法器,而仅增加了9个加法器。
3 本文设计
针对基于Karatsuba算法设计的单精度浮点数乘法器依然存在乘法器,限制了运算速度的提升,本文对原Karatsuba算法进行了改进,并将该改进算法应用于单精度浮点乘法器设计。具体地,本设计在将24 bit乘法分解为8 bit乘法和9 bit乘法的基础上,再次复用Karatsuba算法,将8 bit和9 bit的乘法运算进一步分解,使得原有的24 bit乘法运算被分解为3 bit和4 bit的乘法运算,从而使用更少的低位宽乘法器来实现更高比特的乘法运算,可以减少乘法器的使用,进一步简化电路结构,达到提高运算速度的目的。另一方面,本设计同时结合Vedic算法设计一种基于加法运算的乘法器,替换Karatsuba尾数乘法架构中的3 bit和4 bit的乘法器,从而利用少量低比特加法器实现乘法运算,降低硬件资源消耗和降低关键延时,提高单精度浮点乘法器运算速度。如图2所示,单精度浮点乘法器由数据分割处理模块、符号位运算模块、阶码运算模块、尾数运算模块、标准化模块等5个模块组成。
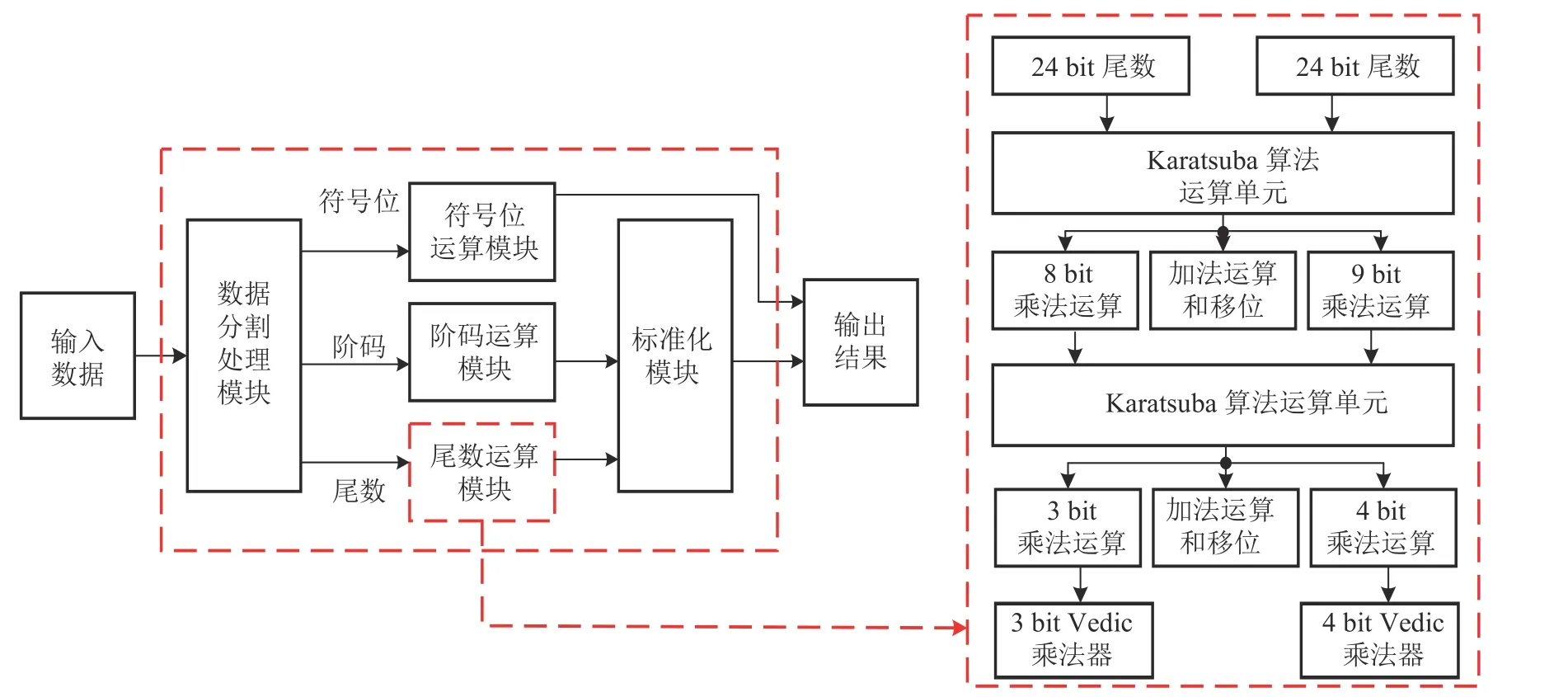
图2 浮点数乘法器的整体结构
如图2所示,本文对24 bit的尾数运算(尾数部分在最高位隐藏了一个“1”,在计算浮点数乘法时要补上“1”)进行改进。本文的设计步骤主要分为3个阶段:
1)将24 bit的乘法运算通过Karatsuba算法分解为8 bit的乘法器、9 bit的乘法器、加法器和移位寄存器[1];
2)再次利用Karatsuba算法对8 bit乘法器和9 bit乘法器进行分解,分解成3 bit的乘法器和4 bit的乘法器、加法器和移位寄存器;
3)使用Vedic算法设计的3 bit Vedic乘法器和4 bit Vedic乘法器来代替阶段2)的3 bit乘法器和4 bit乘法器。
以下是各个阶段的具体实现方法。
阶段1):由式(11)可知,将24 bit的乘法运算分解为8 bit和9 bit乘法运算;阶段2):对式(5)~(10)中的乘法运算进行分解,拆分为3 bit和4 bit的乘法运算。式(5)~(7)中的乘法运算是8 bit的乘法运算,式(8)~(10)中的乘法运算是9 bit的乘法运算。9 bit乘法运算的分解方法和24 bit乘法运算的分解方法一样,把输入进行划分,n的取值变为3。8 bit乘法运算的分解方法为:

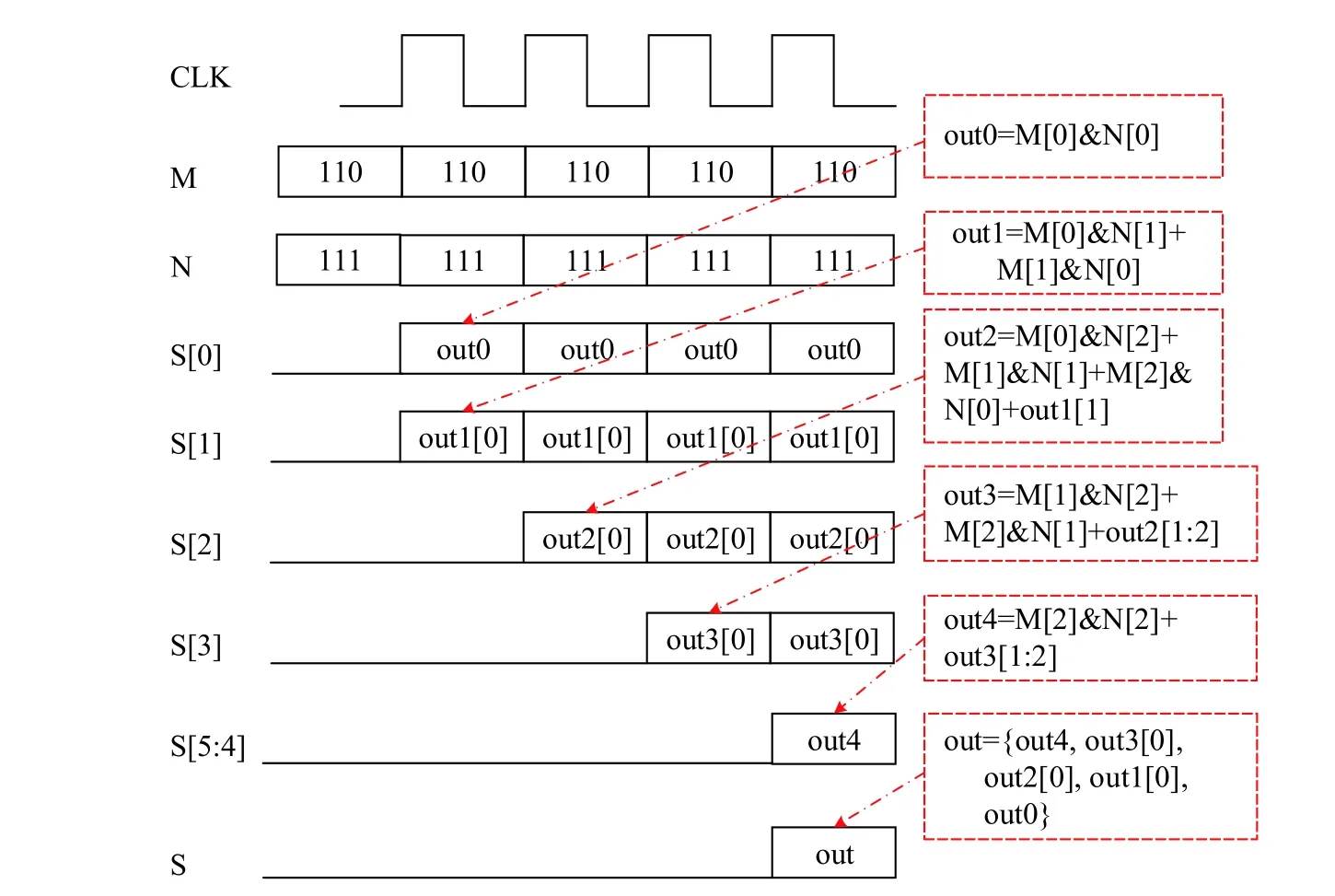
图3 Vedic算法设计3 bit乘法器的流程图
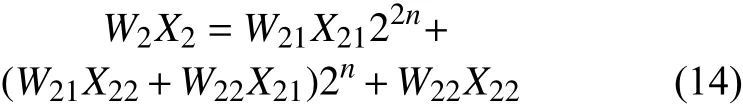
式中,W21、W22、X21、X22分别是W2、X2的高4位和低4位,此时n的取值为4。阶段3):为了进一步提高单精度浮点乘法器的运算速度,利用Vedic算法设计的3 bit Vedic乘法器和4 bit Vedic乘法器来代替Karatsuba算法分解后的3 bit、4 bit的乘法器。按照Vedic算法的思想使用加法器来搭建乘法器时使用了流水线设计方法。
Vedic算法可通过加法器来实现乘法运算,其具有运算简单,实现的乘法运算速度快、效率高、硬件资源消耗少的特点[12]。基于Vedic算法设计3 bit Vedic乘法器流程如图3所示。
如图3所示,M是二进制的(110)2,N是二进制的(111)2。M2、M1、M0分别代表M的高1位、中间1位、低1位,N2、N1、N0分别代表N的高1位、中间1位、低1位。运算步骤如下:
1)M0与N0相与的结果out0作为输出结果的最低位S[0];
2)M1与N0相与的结果再加上M0与N1相与的结果得到值out1,将out1[0]作为输出结果的次低位S[1];
3)out1[1]作为加数与M0和N2相与的值、M1和N1相与的值、M2和N0相与的值相加得到结果out2,将out2[0]作为输出结果的S[2];
4)out2[1:2]作为加数与M1和N2相与的值、M2和N1相与的值相加得到的结果out3,将out3[0]作为输出结果的S[3];
5)out3[1:2]作为加数与M2和N2相与的值相加得到结果out4,将out4作为输出结果的S[5:4]。拼接S[5:4]、S[3]、S[2]、S[1]、S[0]的值得到输出结果S。
4 bit Vedic乘法器设计流程与3 bit Vedic乘法器设计流程类似。如图4所示,把式(8)中的W2加W1的结果A分割为高3位A2、中间3位A1、低3位A0,X2加X1的结果B分割为高3位B2、中间3位B1、低3位B0。按照Karatsuba算法的思想可以通过3 bit的Vedic乘法器(VM表示Vedic multiplier)和4 bit的Vedic乘法器实现9 bit的乘法运算。9 bit乘法器的整体设计框如图4所示。

图4 9 bit乘法器的硬件设计框图
同理,按照Karatsuba算法的思想通过8 bit乘法器和9 bit乘法器实现24 bit尾数相乘运算。24 bit乘法器的整体设计框如图5所示。
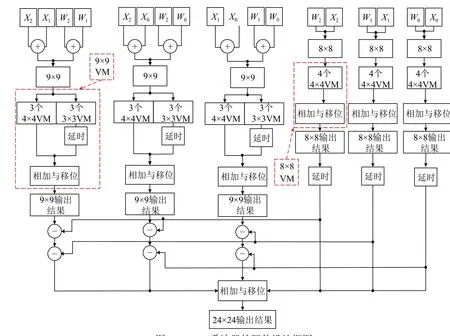
图5 24 bit乘法器的硬件设计框图
由图5可知,得到24 bit尾数相乘的结果仅需要21个4 bit Vedic乘法器和9个3 bit Vedic乘法器。相比于文献[3]的64个3 bit Vedic乘法器,本文设计减少了Vedic乘法器的迭代次数。
4 算法性能仿真与验证
本文设计的单精度浮点乘法器在Modelsim平台上进行仿真。随机产生3000组32位浮点数测试数据ain和bin,执行完乘法运算后,在输出数据有效指示信号dout_vld为高电平时得到输出结果dout。
图6给出了本文设计的单精度浮点乘法器的一个测试案例的仿真结果。由仿真结果可知,输入ain以十六进制表示为3f000000(即十进制实数0.5),输入bin以十六进制表示为3f400000(即十进制实数0.75),输出结果dout以十六进制表示为3ec00000 (即十进制实数0.375)。根据仿真波形可得,单精度浮点乘法器的输出结果需要延时5拍时钟,仿真结果证明了本文所提出的单精度浮点乘法器设计方法的正确性。

图6 浮点数乘法器的仿真结果
为了进一步证明本文设计的有效性,利用Quartus II 64-bit 13.0.1平台在相同的芯片Cyclone II EP2C5F256C6、Cyclone IV EP4CE6F17C6上综合。表1给出了本文设计的单精度浮点乘法器与文献[1]算法、文献[3]算法设计的单精度浮点乘法器及Altera公司开发的浮点数乘法IP核的性能比较。
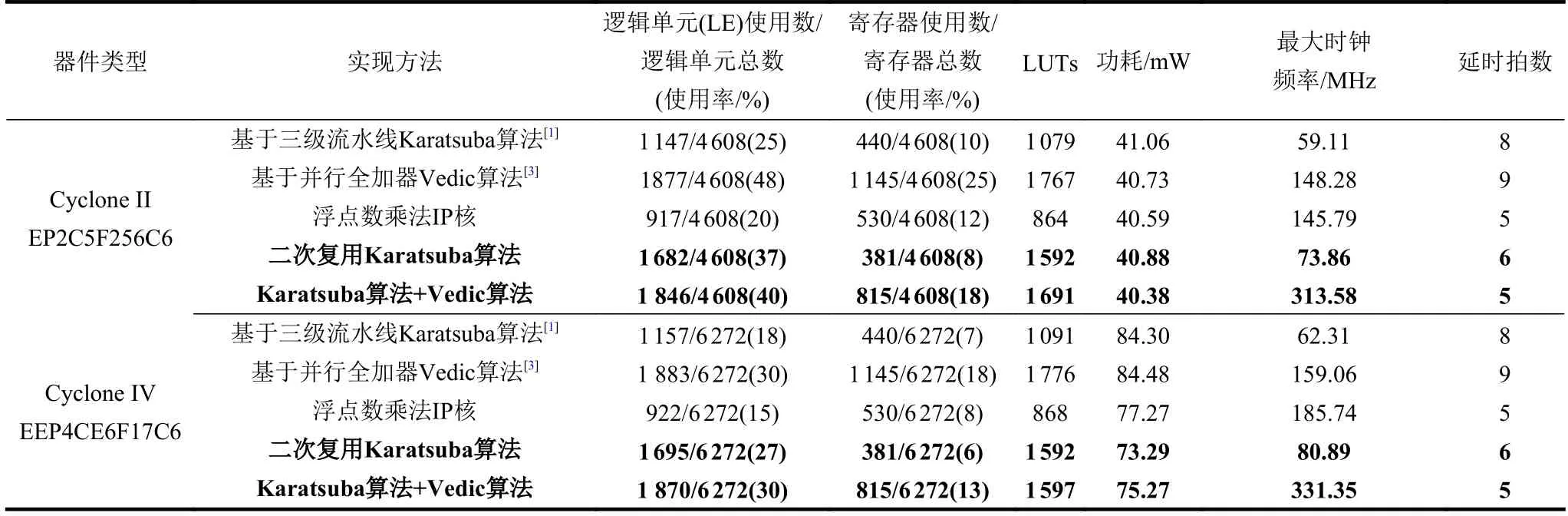
表1 5种浮点乘法器的性能参数对比
在相同的芯片Cyclone II EP2C5F256C6、Cyclone IV EP4CE6F17C6下,文献[1]设计的单精度浮点乘法器最大时钟频率分别为59.11MHz、62.31 MHz。文献[1]消耗的资源较少,是因为沿用了资源消耗少但工作频率低的乘法器。文献[3]设计的单精度浮点乘法器最大运行时钟频率分别为148.28 MHz、159.06 MHz。相比于文献[1],文献[3]设计的单精度浮点乘法器的最大运行时钟频率提高了2.5倍,但是逻辑单元、寄存器及LUTs使用数量分别平均增多了约730个、700个和690个。本文二次复用Karatsuba算法把文献[1]的9 bit和8 bit乘法运算分解为3 bit和4 bit乘法运算。本文二次复用Karatsuba算法实现的单精度浮点乘法器的最大时钟频率分别增大到73.86 MHz、80.89 MHz。二次复用Karatsuba算法的实验结果证明,文献[1]设计的单精度浮点乘法器的最大时钟频率受限于乘法器。本文融合Karatsuba算法和Vedic算法两者优点设计的单精度浮点乘法器输出结果需要延时5拍时钟,相比于文献[1]的8拍时钟、文献[3]的9拍时钟,延时更短,响应时间更快。本文融合Karatsuba算法和Vedic算法优点实现的单精度浮点乘法器的最大时钟频率是相对最优的,分别达到313.58 MHz、331.35 MHz。相比于文献[1]、文献[3]、浮点数乘法IP核,本文融合Karatsuba算法和Vedic算法两者优点设计的单精度浮点乘法器的最大时钟频率分别平均提高了5.30倍、2.10倍、1.97倍。本文融合Karatsuba算法和Vedic算法优点设计的单精度浮点乘法器比文献[3]的逻辑单元、寄存器及LUTs分别平均降低了22个、330个、127个,比文献[1]的逻辑单元、寄存器及LUTs分别平均增加了706个、375个、559个,比浮点数乘法IP核的逻辑单元、寄存器及LUTs分别平均增加了938个、285个、778个,但是在硬件资源可以接受的范围下获得了更高的最大时钟频率,降低了输出延时,提高了运算速度。同时本文融合Karatsuba算法和Vedic算法优点设计的单精度浮点乘法器的功耗分别是40.38 mW、75.27 mW。在芯片Cyclone II EP2C5F256C6下,本文设计的单精度浮点乘法器相比于文献[1]、文献[3]、浮点数乘法IP核分别降低了0.68 mW、0.35 mW、0.21 mW。在芯片Cyclone IV EP4CE6F17C6下,本文设计的单精度浮点乘法器相比于文献[1]、文献[3]、浮点数乘法IP核分别降低了9.03 mW、9.21 mW、3.0 mW。本文所提出的设计方法在需要计算大量数据的人工智能领域更具有优势,更能满足计算实时性的需求,具有一定的实用价值。
5 结束语
本文优化了Karatsuba算法并利用该算法设计了基于IEEE754标准的单精度浮点乘法器。设计充分利用了Karatsuba算法可以减少乘法器数量的优点和Vedic算法可以用简单的加法器实现乘法功能而门延迟和面积增加很缓慢的优点,通过二次复用Karatsuba算法来减少乘法器的数量,降低单精度浮点乘法器复杂度;再通过Vedic算法设计的3 bit、4 bit Vedic乘法器来替换本文设计中需要用到的3 bit乘法器和4 bit乘法器,并在Vedic算法设计的3 bit乘法器、4 bit的乘法器中运用了流水线设计方法来优化结构,提高设计的运行时钟频率、运算效率及运算速度。在相同的平台和芯片型号下,本文设计的单精度浮点乘法器的最大时钟频率相比于文献[1]、文献[3]、浮点数乘法IP核分别平均提高了5.30倍、2.10倍、1.97倍。
本文研究工作得到羊城创新创业领军人才支持计划的资助(2019019),在此表示感谢。
